Minifloat
Als Minifloats bezeichnet man Zahlen in einem Gleitkommaformat mit nur wenigen Bits. Minifloats sind für numerische Rechnungen nicht geeignet, werden jedoch gelegentlich für Spezialzwecke oder in der Ausbildung eingesetzt.
Minifloats mit 16 Bit werden auch als halbgenaue Zahlen (als Gegensatz zu einfach und doppelt genauen Zahlen) bezeichnet. Es gibt auch Minifloats mit 8 Bit und weniger. Viele Minifloats werden nach den Prinzipien der IEEE-754-Norm definiert und enthalten spezielle Werte für NaN und unendlich. Normalisierte Zahlen sind dann mit einem Exzess-Exponenten gespeichert. In der überarbeiteten Norm IEEE 754-2008 sind binäre Minifloats mit 16 Bit enthalten.[1]
Der Standard G.711 zur Kodierung von Audiodaten von ITU-T, der in Audiodateien des Typs Au und für Telefonverbindungen eingesetzt wird, benutzt bei der sogenannten A-law-Codierung 1.3.4-Minifloats um eine vorzeichenbehaftete 13-Bit-Ganzzahl als 8-Bit-Wert darzustellen.
Minifloats werden neben dem Einsatz als Übungsformat in Lehrveranstaltungen auch in der Computergraphik zur Darstellung ganzer Zahlen verwendet. Werden gleichzeitig die IEEE 754-Prinzipien zugrundegelegt, so muss die kleinste denormalisierte Zahl gleich eins sein. Daraus ergibt sich der zu verwendende Exzess-Wert (Bias). Das folgende Beispiel demonstriert die Herleitung sowie die zugrundeliegenden Prinzipien.
Beispiel
Ein Minifloat in einem Byte (8 Bit) mit 1 Vorzeichenbit, 4 Exponentenbits und 3 Mantissenbits (kurz: eine (1.4.3.-2)-Zahl; die Klammer enthält alle IEEE-Parameter) soll zur Darstellung ganzer Zahlen nach IEEE 754-Prinzipien konstruiert werden. Dazu muss im Wesentlichen der Biaswert sinnvoll festgelegt werden. Der (noch) unbekannte Exponent (gespeicherter Wert e – Biaswert b) wird vorläufig mit x bezeichnet. Zahlen in anderen Systemen werden mit …() gekennzeichnet: 5 = 101(2) = 10(5). Das Bitmuster wird durch Leerzeichen in seine Bestandteile gegliedert.
Darstellung der Null
0 0000 000 = 0
Denormalisierte Zahlen
Die Mantisse wird mit 0. ergänzt:
(kleinste denormalisierte Zahl) ... (größte denormalisierte Zahl)
Normalisierte Zahlen
Die Mantisse wird mit 1. ergänzt:
0 0001 000 = 1.000(2) * 2^x = 1 * 2^x = 8 (kleinste normalisierte Zahl) 0 0001 001 = 1.001(2) * 2^x = 1.125 * 2^x = 9 ... 0 0010 000 = 1.000(2) * 2^(x+1) = 1 * 2^(x+1) = 16 = 1.6e1 0 0010 001 = 1.001(2) * 2^(x+1) = 1.125 * 2^(x+1) = 18 = 1.8e1 ... 0 1110 000 = 1.000(2) * 2^(x+13) = 1.000 * 2^(x+13) = 65536 = 6.5e4 0 1110 001 = 1.001(2) * 2^(x+13) = 1.125 * 2^(x+13) = 73728 = 7.4e4 ... 0 1110 110 = 1.110(2) * 2^(x+13) = 1.750 * 2^(x+13) = 114688 = 1.1e5 0 1110 111 = 1.111(2) * 2^(x+13) = 1.875 * 2^(x+13) = 122880 = 1.2e5 (größte Normalisierte Zahl)
(Die Darstellungen rechts berücksichtigen die Genauigkeit, denn natürlich kann man mit drei Bit keine fünf oder sechs Stellen speichern.)
Unendlich
0 1111 000 = unendlich
Der numerische Wert von unendlich ohne die IEEE 754 Interpretation wäre
(numerischer Wert von unendlich)
Nichtzahlen
0 1111 xxx = NaN
Der numerische Wert der größten NaN ohne die IEEE 754 Interpretation wäre
(numerischer Wert von NaN)
Herleitung
Wenn die kleinste denormalisierte Zahl gleich eins sein soll, muss nach der zweiten Zeile x = 3 sein. Daraus folgt ein Exponenten-Bias (Exzess-Wert) von −2. Vom gespeicherten Exponent muss jeweils −2 subtrahiert werden (+2 addiert werden), um zum rechnerischen Exponenten x zu kommen.
Diskussion dieses Beispiels
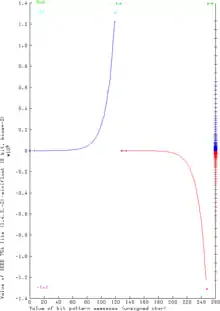
Der Vorteil solcher ganzzahliger Minifloats in einem Byte ist der wesentlich größere Wertebereich von −122880 … 122880 gegenüber Darstellungen im Zweierkomplement mit −128 … 127. Dafür sinkt die Genauigkeit rapide ab, da stets nur 4 signifikante Bitstellen existieren. Dementsprechend groß sind die Lücken im Bereich der größten normalisierten Zahlen.
Diese Minifloat-Darstellung kann nur 242 verschiedene Zahlen darstellen (sofern man +0 und −0 als verschieden ansieht), da es 14 verschiedene Bitmuster gibt, die keine Zahl darstellen (NaN).
Interessant ist die Übereinstimmung der Bitmuster von Minifloatzahlen und Integer-Zahlen zwischen 0 und 16. Erst das Bitmuster 00010001 wird als Minifloat 18, jedoch als Integerzahl 17 interpretiert.
Für negative Zahlen stimmt diese Übereinstimmung jedoch nicht mehr, da negative Integer-Zahlen üblicherweise im Zweierkomplement repräsentiert werden.
Deutlich kann man an der (senkrechten) reellen Zahlenachse auf der rechten Seite der Graphik die variierende Dichte der Gleitkommazahlen erkennen – eine charakteristische Eigenschaft aller Gleitkommasysteme. Diese variierende Dichte bedingt den exponentialfunktionsartigen Verlauf der Graphik.
Obwohl auch viele Informatiker gefühlsmäßig glauben, dass die Kurve stetig differenzierbar ist, erkennt man deutlich die „Knicke“ an den Stellen, an denen jeweils der Exponentenwert wechselt. Solange der Exponent konstant bleibt, sind die nur durch unterschiedliche Mantissen dargestellten Gleitkommazahlen sogar linear verteilt – zwischen zwei „Knicken“ ist die Kurve eine Gerade. Natürlich liegt nicht einmal eine Kurve vor, da Gleitkommazahlen lediglich eine diskrete endliche Menge von Punkten darstellen. Die Aussage bezieht sich also auf eine möglichst gut durch die endliche Punktmenge interpolierte Kurve. In der Praxis liegen normalerweise so viele Punkte vor, dass sie für den Betrachter wie eine stetige Kurve wirken (bei double sind es 264, also etwa 1019 Punkte).
Arithmetik mit Minifloats
Addition
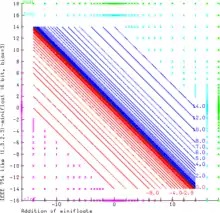
Die Graphik demonstriert die Addition zweier noch kleinerer (1.3.2.3)-Minifloats mit je 6 Bit. Bei diesem Modell werden reelle Zahlen nach allen IEEE-754-Prinzipien dargestellt. Ein NaN-Operand oder die Rechnung „Inf – Inf“ resultieren in einem NaN-Ergebnis. Inf kann ohne Änderung (mit endlichen Werten) vergrößert oder verkleinert werden. Auch endliche Summen können unendliche Ergebnisse haben (14,0+3,0). Der endliche Bereich (Operanden und Ergebnis sind endlich) wird durch die Linien mit x+y=c dargestellt, wobei c immer einer der darstellbaren Minifloatwerte ist.
Subtraktion, Multiplikation und Division
Die restlichen arithmetischen Operationen kann man ähnlich darstellen:
 Subtraktion
Subtraktion Multiplikation
Multiplikation Division
Division
Wie mit allen Multiplikationen mit Gleitkommazahlen lassen sich ca. 25 Prozent der Ergebnisse nicht im Zahlenformat der Operanden darstellen.
Weblinks
- https://www.khronos.org/registry/OpenGL/extensions/ARB/ARB_half_float_pixel.txt Minifloats für graphische Zwecke mit 16 Bit
Einzelnachweise
- IEEE 754-2008: Standard for Floating-Point Arithmetic, IEEE Standards Association, 2008, doi:10.1109/IEEESTD.2008.4610935