Bildregistrierung

Bildregistrierung ist ein wichtiger Prozess in der digitalen Bildverarbeitung und dient dazu, zwei oder mehrere Bilder derselben Szene, oder zumindest ähnlicher Szenen, bestmöglich in Übereinstimmung miteinander zu bringen. Dabei wird eines der Bilder als Referenzbild festgelegt, die anderen werden Objektbilder genannt. Um diese optimal an das Referenzbild anzupassen, wird eine ausgleichende Transformation berechnet. Die zu registrierenden Bilder unterscheiden sich voneinander, weil sie von unterschiedlichen Positionen, zu unterschiedlichen Zeitpunkten oder mit unterschiedlichen Sensoren aufgenommen wurden.

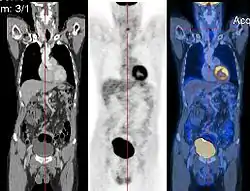
PET/CT: links CT, Mitte PET, rechts Resultat einer Registrierung (mit Falschfarbendarstellung)

Bildregistrierungsverfahren sind vor allem in der medizinischen Bildverarbeitung häufig. Die mit verschiedenen bildgebenden Verfahren (Modalitäten) aufgenommenen Bilder werden aneinander angeglichen, um aus ihrer Kombination bessere Erkenntnisse zu gewinnen. Werden z. B. MRT-Bilder, die Weichteilgewebe oder Gehirnstrukturen gut darstellen, mit PET-Bildern überlagert, die bestimmte Stoffwechselprozesse sichtbar machen, kann man nachvollziehen, in welchen Gehirnbereichen bestimmte Stoffwechselprozesse stattfinden. Die Überlagerung wird auch als Bildfusion bezeichnet.

Ein weiteres Anwendungsbeispiel ist das Zusammenfügen mehrerer Satellitenbilder zu einer großen Karte. Da die Erdoberfläche gekrümmt ist und sich die Position des Satelliten von Bild zu Bild ändert, kommt es innerhalb der Bilder zu kleinen Verzerrungen, die mit Registrierungsverfahren aneinander angeglichen werden können – siehe auch Bildkorrelation.

Das Ziel der Bildregistrierung ist, jene Transformation T zu finden, die ein gegebenes Quellbild (Objektbild) F bestmöglich mit einem Zielbild (Referenzbild) G in Übereinstimmung bringt. Dazu wird ein Maß D für die Gleichheit oder die Ungleichheit der Bilder charakterisiert. Bildregistrierung ist also ein Optimierungsproblem, bei dem D(T(F), G) zu minimieren ist (falls D die Ungleichheit misst) bzw. zu maximieren (falls D die Gleichheit misst).

Überblick

Wie oben ersichtlich, kann die Anwendung der Bildregistrierung in folgende Bereiche aufgeteilt werden:

Verschiedene Kamerapositionen: Die zu registrierenden Bilder zeigen dasselbe Objekt bzw. dieselbe Szene, wurden aber von verschiedenen Kamerapositionen aufgenommen (siehe Parallaxe). Die Registrierung kann dann genutzt werden, um ein größeres zweidimensionales Sichtfeld zu erhalten oder auch zur 3D-Rekonstruktion.
Verschiedene Zeitpunkte: Die zu registrierenden Bilder zeigen dasselbe Objekt bzw. dieselbe Szene, aber zu unterschiedlichen Zeitpunkten. Mittels Registrierung sind nun Veränderungen, die über die Zeit entstanden sind, feststellbar (Zeitreihenanalyse).
Verschiedene Sensoren: Die zu registrierenden Bilder enthalten dasselbe Objekt bzw. dieselbe Szene, wurden aber mit verschiedenen Sensoren aufgenommen, d. h. mit verschiedenen Kameras oder verschiedenen bildgebenden Verfahren. Das Ziel der Bildregistrierung ist hier, mehr und detailliertere Informationen aus den Bildern zu gewinnen.
Szene-zu-Modell-Registrierung: Ein oder mehrere Bilder eines Objektes bzw. einer Szene werden mit einem Modell des Objektes bzw. der Szene registriert. Die registrierten Bilder können dann mit dem gegebenen Modell verglichen werden.

Wegen der weitgefächerten Anwendungsmöglichkeiten und verschiedenartigen Bilder gibt es kein Registrierungsverfahren, das universell einsetzbar ist. Vielmehr werden Registrierungsverfahren speziell für verschiedene Anwendungen entwickelt, für die sie dann optimal funktionieren. Trotzdem lassen sich die meisten Registrierungsverfahren in folgende vier Hauptschritte unterteilen:

Merkmalsextraktion: Aus den zu registrierenden Bildern werden Merkmale, wie z. B. Ecken, Kanten, Konturen oder Ähnliches manuell oder automatisch detektiert.
Merkmalsanpassung: Die Korrespondenz der extrahierten Merkmalspunkte wird hergestellt.
Transformationsberechnung: Es wird ein geeigneter Transformationstyp, z. B. affin, projektiv oder Ähnliches, gewählt und die Transformationsparameter berechnet.
Transformation: Das Objektbild wird mit der im vorherigen Schritt berechneten Umbildung transformiert. Hierbei kommen auch Interpolationstechniken zum Einsatz.

Merkmalsextraktion

Registrierungsverfahren lassen sich in zwei Kategorien einordnen, die merkmalsbasierten und die flächenbasierten Verfahren. Bei den flächenbasierten Verfahren wird die Registrierung direkt mit den Intensitätswerten durchgeführt, es müssen keine Merkmale extrahiert werden. Der Schritt der Merkmalsextraktion fällt bei diesen Verfahren also weg.

Die zweite Kategorie sind die merkmalsbasierten Verfahren, bei denen aus den Bildern eine bestimmte, in der Regel relativ kleine, Anzahl von Merkmalen extrahiert wird. Dies geschieht entweder manuell oder automatisch. Bei der manuellen Merkmalsextraktion werden von einer Person in den Bildern signifikante Punkte markiert. Bei automatischen Verfahren wird in den Bildern nach markanten und vor allem in allen Bildern auffindbaren Merkmalen gesucht. Die gewählten Merkmale sollten dabei möglichst über das gesamte Bild verteilt liegen und sich nicht auf bestimmte Regionen konzentrieren. Die Registrierung erfolgt dann dadurch, dass die gewählten Merkmale in Übereinstimmung gebracht werden. Im Folgenden werden die einzelnen Merkmalsgruppen näher erläutert:

Regionen: Als Regionenmerkmale eignen sich Flächen im Bild, die sich von den sie umgebenden Flächen deutlich abheben. Dies können in Satellitenbildern z. B. Seen sein. Regionen werden meist durch ihren Schwerpunkt repräsentiert und können durch Segmentierungsverfahren detektiert werden.
Linien: Linien oder Kanten können im Bild als Konturen von Regionen oder eben als Linien selbst vorhanden sein. Sie können durch die Paare ihrer Endpunkte oder ihren Mittelpunkt repräsentiert und mittels Kantendetektion extrahiert werden.
Punkte: Punkte können im Bild als Schnittpunkte von Linien oder Ecken von Konturen gegeben sein. Sie können durch Eckendetektoren extrahiert werden.

Der Vorteil der merkmalsbasierten Verfahren gegenüber den flächenbasierten ist einerseits der in der Regel geringere Rechenaufwand bei der Merkmalsanpassung, da die Anzahl der Merkmale nicht allzu groß gewählt wird und andererseits die geringere Rauschanfälligkeit, da die Registrierung nicht direkt mit den Intensitätswerten durchgeführt wird. Der Nachteil aber ist eben die Merkmalsextraktion selbst, die einen zusätzlichen Verarbeitungsschritt darstellt. Oft ist es bei der automatischen Merkmalsextraktion nicht einfach, Merkmale zu wählen, die in allen Bildern gut wieder zu finden sind, oder aber die Anzahl der Merkmale möglichst klein zu halten. Deshalb sollten merkmalsbasierte Verfahren nur gewählt werden, wenn zu erwarten ist, dass in allen Bildern wenige gleichmäßig über das Bild verteilte und gut zu extrahierende Merkmale vorhanden sind.

Merkmalsanpassung

Flächenbasierte Verfahren

Bei den flächenbasierten Verfahren wird der Schritt der Merkmalsextraktion mit dem der Merkmalsanpassung vermischt, da hier ja in gewissem Sinne jeder Bildpunkt ein Merkmalspunkt ist. Die Herstellung der Korrespondenz zwischen dem Objektbild und dem Referenzbild kann durch Fenster bestimmter Größe erfolgen, so dass die Korrespondenz Fenster für Fenster hergestellt wird. Es kann aber auch das gesamte Bild verwendet werden. Für die Registrierung wird dann entweder eine Funktion, die die Verschiedenheit des Objektbildes und des Referenzbildes, oder eine Funktion, die die Übereinstimmung des Objektbildes mit dem Referenzbild angibt, verwendet. Diese Funktion muss dann entsprechend minimiert bzw. maximiert werden.

Korrelations-Methoden

Ein weitverbreiteter Ansatz bei flächenbasierten Verfahren ist die Kreuzkorrelationsfunktion. Diese wird gewöhnlich beim Template-Matching oder in der Mustererkennung genutzt. Seien f und g zwei Bildausschnitte gleicher Dimension aus dem Objekt- bzw. Referenzbild. Mit Hilfe der normalisierten Kreuzkorrelationsfunktion

NCCF(u,v)={\frac {\sum _{x}\sum _{y}f(x,y)g(x+u,y+v)}{{\sqrt {\sum _{x}\sum _{y}f(x,y)^{2}}}{\sqrt {\sum _{x}\sum _{y}g(x+u,y+v)^{2}}}}}

wird ein Wert berechnet, der im Bereich [0..1] liegt und die Ähnlichkeit von f und g repräsentiert. Je höher der Wert ist, desto ähnlicher sind die Bildausschnitte. Dieses Ähnlichkeitsmaß wird nun für Bildausschnittspaare vom Objekt- und Referenzbild berechnet. Die Bildausschnitte mit dem höchsten Wert werden dann als die korrespondierenden festgelegt. Diese Methode funktioniert nur, wenn der Unterschied zwischen dem Objektbild und dem Referenzbild aus Translationen besteht. Bei Rotation, Skalierung oder anderen Verformungen scheitert das Verfahren in dieser Form.

Fourier-Methoden

Falls die Bilder mit frequenzabhängigem Rauschen behaftet sind, bieten die Fourier-Methoden eine bessere Lösung als die Korrelations-Methoden. Außerdem lässt sich die Berechnungszeit gegenüber den Korrelations-Methoden reduzieren. Translation, Rotation und Skalierung haben ihr entsprechendes Gegenstück im Frequenzraum, sind somit also durch diese Methoden realisierbar. Die Berechnung der Fourier-Koeffizienten eines Bildes lässt sich effizient realisieren, entweder durch Implementierung in Hardware oder durch Nutzen der schnellen Fourier-Transformation (FFT).

Eine Möglichkeit, zwei Bilder, die sich lediglich durch eine Translation voneinander unterscheiden, zu registrieren, bietet die Phasenkorrelation. Die Phasenkorrelation beruht auf dem Shift-Theorem.

Seien zwei Bilder f und g gegeben, die sich durch eine Translation (u, v) unterscheiden, d. h. es gilt f(x, y) = g(x+u, y+v). Dann hängen deren Fouriertransformationen wie folgt voneinander ab:

F_{g}(\omega _{x},\omega _{y})=e^{-j(\omega _{x}u+\omega _{y}v)}F_{f}(\omega _{x},\omega _{y})

.

Die Fouriertransformation der Bilder f und g unterscheidet sich also nur durch eine Phasenverschiebung, die direkt mit der Translation in Verbindung steht. Mittels des Kreuzleistungsspektrums der Bilder f und g

{\frac {F_{f}(\omega _{x},\omega _{y})F_{g}^{*}(\omega _{x},\omega _{y})}{\left|F_{f}(\omega _{x},\omega _{y})F_{g}^{*}(\omega _{x},\omega _{y})\right|}}=e^{j(\omega _{x}u+\omega _{y}v)}

kann man die Phasenverschiebung berechnen. Dazu sucht man nach dem Maximum in der inversen Fouriertransformation des Kreuzleistungsspektrums. Die Position des Maximums liefert dann die Translationsparameter.

Auf der Transinformation basierende Methoden

Methoden, die die Transinformation der Bilder nutzen, zeigen vor allem bei Bildern gute Ergebnisse, bei denen die Intensitätswerte stark variieren. Diese Variation tritt z. B. bei Bildern auf, die mit unterschiedlichen Sensoren, wie beispielsweise MRT und CT, aufgenommen wurden.

Wichtig für die Erklärung der wechselseitigen Information ist die Entropie

H(X)=-\sum _{x\in X}p(x)\log _{2}p(x)

,

wobei X eine Zufallsvariable ist, x ist ein diskreter Wert der Zufallsvariablen X und p ist eine Wahrscheinlichkeitsdichte. Im Fall der Bildregistrierung liegt es nahe, dass die Zufallsvariable X die Intensitätswerte eines Bildes darstellt. Die Entropie ist dann ein Maß für die Unordnung eines Bildes. Sind alle Intensitätswerte eines Bildes gleich wahrscheinlich, dann ist die Entropie am größten. Enthält das Bild nur einen einzigen Intensitätswert, so ist die Entropie null. Bei der Bildregistrierung benötigt man aber die gemeinsame Entropie zweier Zufallsvariablen X und Y

H(X,Y)=-\sum _{x\in X}\sum _{y\in Y}p(x,y)\log _{2}p(x,y)

,

da ja mindestens zwei Bilder miteinander verglichen werden müssen. Wenn dieses Maß minimal ist, dann sind die Bilder in bestmöglicher Übereinstimmung. Aber die gemeinsame Entropie sinkt nicht nur, wenn die Bilder besser aneinander angepasst werden, sondern auch, wenn die Entropie eines der Bilder sinkt. Daher sollte ein Maß für die Übereinstimmung auch die Entropien der einzelnen Bilder berücksichtigen. Die Transinformation

I(X;Y)=H(X)+H(Y)-H(X,Y)=\sum _{x\in X}\sum _{y\in Y}p(x,y)\log _{2}{\frac {p(x,y)}{p(x)p(y)}}

,

Darstellung der Entropie (links), gemeinsamen Entropie (mitte) und der Transinformation (rechts) als Venn-Diagramme.

ist ein solches Maß. Die Transinformation wird maximal, wenn die gemeinsame Entropie sinkt. Das Bild rechts zeigt Venn-Diagramme, die die verschiedenen Maße darstellen. Dort kann auch noch einmal nachvollzogen werden, dass die Transinformation maximal ist, wenn die gemeinsame Entropie minimal ist. Das Ziel bei der Registrierung mit Transinformation ist es also, diese zu maximieren, d. h. die Bilder sind in bestmöglicher Übereinstimmung, wenn die Transinformation maximal ist. Um gute Schätzungen für die Transinformation zu erhalten, ist es notwendig, eine gute Schätzung für die Wahrscheinlichkeitsdichte p zu haben. Es müssen also möglichst viele Bildpunkte einbezogen werden, was auch ein Nachteil ist, da die Registrierung somit sehr aufwendig wird.

Merkmalsbasierte Verfahren

Seien zwei Mengen von Merkmalen gegeben. Eine enthält die Merkmale im Objektbild, die andere die Merkmale im Referenzbild. Die Merkmale werden durch sogenannte Kontrollpunkte repräsentiert. Dies können die Merkmale selbst sein, falls es sich bei den Merkmalen um Punkte handelt, oder Endpunkte von Linien, Schwerpunkte von Regionen oder ähnliches. Ziel der Merkmalsanpassung ist es, die paarweise Korrespondenz der Merkmale des Objektbildes mit denen des Referenzbildes herzustellen.

Methoden, die räumliche Relationen nutzen

Bei diesen Methoden wird die Information über die Distanz der Kontrollpunkte untereinander und deren räumliche Verteilung ausgenutzt, um die Korrespondenz zwischen den Kontrollpunkten des Objektbildes und denen des Referenzbildes herzustellen.

Eine Möglichkeit die Anpassung durchzuführen ist die folgende. Es werden n Kontrollpunkte im Objektbild ausgewählt. Danach werden im Referenzbild n Kontrollpunkte als die zu den ausgewählten Kontrollpunkten im Objektbild korrespondierenden festgelegt. Anhand dieser Korrespondenz wird die Transformation berechnet und durchgeführt. Danach wird überprüft wie viele der restlichen Kontrollpunkte übereinander oder zumindest ausreichend nahe beieinander liegen. Ist die Prozentzahl der aufeinanderliegenden restlichen Kontrollpunkte unter einem bestimmten Schwellwert, dann müssen zwei neue Kontrollpunkte im Referenzbild bestimmt werden und der Vorgang wird wiederholt.

Methoden, die invariante Deskriptoren nutzen

Eine weitere Methode, die Korrespondenz zwischen den Merkmalen herzustellen, ist das Ausnutzen bestimmter Eigenschaften, die die Merkmale charakterisieren. Diese Eigenschaften werden Deskriptoren genannt und sollten möglichst invariant gegenüber den erwarteten Bildverzerrungen sein. Die Deskriptoren sollten folgende Bedingungen erfüllen:

Invarianz: Die Deskriptoren der korrespondierenden Merkmale des Objektbildes und des Referenzbildes sollten die gleichen sein.
Einzigartigkeit: Zwei unterschiedliche Merkmale sollten unterschiedliche Deskriptoren haben.
Stabilität: Die Deskriptoren eines Merkmals, welches verformt ist, sollten ähnlich denen des unverformten Merkmals sein.
Unabhängigkeit: Falls die Deskriptoren ein Vektor sind, sollten dessen Elemente funktional unabhängig voneinander sein.

Es können aber nicht immer alle diese Bedingungen gleichzeitig erfüllt werden. Also muss ein geeigneter Kompromiss bei der Wahl der Deskriptoren gefunden werden. Die Auswahl der Deskriptoren ist abhängig von den Charakteristiken der Merkmale und der erwarteten Verformung zwischen dem Objektbild und dem Referenzbild. Sind die Merkmale z. B. Regionen und besteht die Verformung nur aus Translation und Rotation, so kann als Deskriptor die Fläche einer Region gewählt werden, da diese bei Rotation und Translation gleich bleibt. Kommt aber noch eine Skalierung hinzu, so ist die gewählte Eigenschaft nicht mehr invariant bezüglich der Transformation. Bei der Merkmalsanpassung werden dann die Merkmale aus dem Objektbild und dem Referenzbild als korrespondierend bestimmt, deren Deskriptoren am ähnlichsten sind.

Invariante Deskriptoren können auch genutzt werden, wenn nicht vorher explizit Merkmale extrahiert wurden, sondern ein Fenster über das gesamte Bild läuft und dann jeweils für dieses Fenster die Invarianten berechnet werden.

Transformationsberechnung

Nachdem im letzten Abschnitt die Korrespondenz zwischen den Merkmalen hergestellt wurde, wird in diesem Abschnitt beschrieben, wie die Transformation konstruiert wird, mit der man das Objektbild transformiert, um dieses an das Referenzbild anzupassen. Die Korrespondenz der Kontrollpunkte des Objektbildes und des Referenzbildes, sowie die Voraussetzung, dass die korrespondierenden Kontrollpunkte so nah wie möglich aneinander transformiert werden sollen, fließen in das Design der Transformation ein.

Die Aufgabe, die es zu lösen gilt, ist die Auswahl einer Familie von Funktionen und die Berechnung der Parameter der Abbildungsfunktion. Die Familie von Funktionen muss hinsichtlich der zu erwartenden Bildunterschiede und der nötigen Genauigkeit der Transformation gewählt werden. Der einfachste Fall ist eine Translation. Dabei müssen nur zwei Parameter berechnet werden. Komplexer sind z. B. affine oder perspektivische Transformationen. Je komplexer die Familie von Funktionen ist, desto größer ist auch die Anzahl der zu berechnenden Parameter. Ebenfalls einen Einfluss auf die Wahl der Familie von Funktionen hat die Ursache für die Verschiedenheit der Bilder. So ist z. B. bei perspektivischen Verzerrungen durch unterschiedliche Kamerapositionen die Wahl der Familie von Funktionen als perspektivische Transformation naheliegend.

Die Transformationen können in zwei große Kategorien eingeteilt werden, abhängig vom Umfang der benutzten Daten. Globale Transformationen benutzen alle Kontrollpunkte, um einen Parametersatz für das gesamte Bild zu berechnen. Eine globale Transformation besteht somit aus einer einzigen Funktion, die auf jeden Bildpunkt angewendet wird. Bei den lokalen Transformationen wird das Bild in mehrere Bereiche – im Extremfall ist jeder Bildpunkt ein eigener Bereich – aufgeteilt. Dann werden für jeden Bereich die Parameter berechnet. Somit können auch lokal unterschiedlich starke Unterschiede in den Bildern behandelt werden. Eine lokale Transformation besteht aus mehreren Funktionen, jede für einen Bereich.

Globale Transformationen

Eines der weitverbreiteten globalen Transformationsmodelle benutzt bivariate Polynome niedrigen, meist ersten Grades. Die Ähnlichkeitstransformation ist dabei das einfachste Modell. Durch die folgenden Gleichungen wird der Punkt (x, y) auf den Punkt (x', y') abgebildet:

x'=s(x\cos(\varphi )-y\sin(\varphi ))+t_{x}

y'=s(x\sin(\varphi )+y\cos(\varphi ))+t_{y}

,

wobei $\varphi$ der Rotationswinkel, s der Skalierungsfaktor und $t_{x}$ und $t_{y}$ die Translationsparameter sind. Diese Transformation wird auch formerhaltend genannt, da dadurch Winkel, Strecken und Längenverhältnisse unverändert bleiben. Ein Vorteil ist, dass hierbei nur zwei Kontrollpunkte benötigt werden. Der Nachteil aber ist, dass auf diese Art nur Rotation, Translation und Skalierung realisiert werden können.

Ein allgemeineres Modell ist die affine Transformation. Der Punkt (x, y) wird hierbei wie folgt auf den Punkt (x', y') abgebildet:

x'=\;m_{1}x+m_{2}y+m_{5}

y'=\;m_{3}x+m_{4}y+m_{6}

,

wobei $m_{1}$ und $m_{4}$ die Skalierungsfaktoren, $m_{2}$ und $m_{3}$ die Scherungsfaktoren und $m_{5}$ und $m_{6}$ die Translationsparameter sind. Hierbei werden drei Kontrollpunkte benötigt, aber zusätzlich kann noch die Scherung realisiert werden.

Falls in den zu registrierenden Bildern mit perspektivischen Verzerrungen gerechnet werden muss, sollte die perspektivische Transformation

x'={\frac {a_{1}x+a_{2}y+a_{3}}{1+c_{1}x+c_{2}y}}

y'={\frac {b_{1}x+b_{2}y+b_{3}}{1+c_{1}x+c_{2}y}}

,

verwendet werden. Hier werden nun vier Kontrollpunkte benötigt.

Ist mit komplexeren Verzerrungen in den Bildern zu rechnen, können auch Polynome zweiten oder dritten Grades verwendet werden. Höhergradige Polynome werden meist nicht verwendet. In der Regel werden aber immer mehr Kontrollpunkte für die Registrierung verwendet, als die hier angegebenen Mindestanzahlen. Die Parameter der gewählten Transformation werden dann meist durch die kleinste Quadrate-Methode berechnet, so dass die Transformationsgleichungen die Summe der quadratischen Fehler der Kontrollpunkte minimiert. Dadurch kann es aber vorkommen, dass die Kontrollpunkte nicht exakt übereinander transformiert werden, sondern nur so nahe wie möglich aneinander.

Lokale Transformationen

Triangulation zur Realisierung der stückweisen Interpolation.

Durch globale Transformationen können in den Bildern lokal unterschiedlich starke Unterschiede nur schlecht bzw. gar nicht angeglichen werden. Lokale Transformationen sind dafür besser geeignet. Hierbei besteht die Transformation aus mehreren Funktionen. Für eine Funktion werden dann nicht mehr alle Kontrollpunkte benutzt, sondern jede Funktion hat ihre Kontrollpunkte.

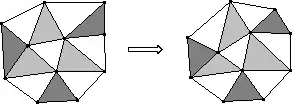
Eine Methode, die lokale Transformationen realisiert, ist die stückweise Interpolation. Dabei wird eine Funktion bestimmt, die zwischen den in Übereinstimmung gebrachten Kontrollpunkten des Objektbildes und des Referenzbildes interpoliert. Eine Möglichkeit dabei ist die Triangulation. Das Bild rechts verdeutlicht, wie mit Hilfe der Kontrollpunkte ein Bild in dreieckige Flächen aufgeteilt werden kann. Die Dreiecke im Bild rechts haben unterschiedliche Farben, um die korrespondierenden Dreiecke besser erkennbar zu machen. Bei der Transformation kommen mehrere Funktionen zum Einsatz, wobei jede innerhalb eines Dreiecks gültig ist. Um mit diesem Vorgehen ausreichend gute Ergebnisse zu erhalten, dürfen die Eckpunkte eines jeden Dreiecks nicht allzu weit auseinander liegen, d. h. es müssen ausreichend viele Kontrollpunkte gegeben sein. Da die Anzahl der benötigten Kontrollpunkte somit sehr hoch ist, ist auch der Berechnungsaufwand dementsprechend hoch.

Radiale Basisfunktionen

Die radialen Basisfunktionen gehören zu den globalen Transformationen, sind aber auch in der Lage, lokale Unterschiede anzupassen. Jede Funktion f, die die folgende Eigenschaft besitzt, ist eine radiale Basisfunktion:

f(x,c)=f(\left\|x-c\right\|)

,

wobei c das Zentrum der Funktion f ist. Bei der Registrierung mit radialen Basisfunktionen ist jeder Kontrollpunkt das Zentrum einer Basisfunktion. Die gesamte Transformation ist dann eine Linearkombination aller dieser radialen Basisfunktionen plus einem Polynom niedrigen Grades. Seien N Kontrollpunkte gegeben, $(u_{i},v_{i})$ die Koordinaten des i-ten Kontrollpunktes und $\omega _{i}$ Gewichte, die angeben, wie stark die Funktion, deren Zentrum der i-te Kontrollpunkt ist, in die gesamte Transformation eingeht. Der Bildpunkt (x, y) wird dann wie folgt in den Bildpunkt (x', y') überführt:

x'=m_{1}x+m_{2}y+m_{3}+\sum _{i=1}^{N}\omega _{i}f(\left\|x-u_{i}\right\|)

y'=m_{4}x+m_{5}y+m_{6}+\sum _{i=1}^{N}\omega _{i}f(\left\|y-v_{i}\right\|)

.

Mittels des Polynoms in den obigen Gleichungen werden die Kontrollpunkte in Übereinstimmung gebracht und mittels der radialen Basisfunktionen werden dann die restlichen Bildpunkte zwischen den Kontrollpunkten interpoliert.

Die meistgenutzte Form bei der Registrierung mit radialen Basisfunktionen sind die Thin-Plate Splines. Dabei ist die radiale Basisfunktion f wie folgt definiert:

f(x,c)=\left\|x-c\right\|^{2}\log(\left\|x-c\right\|)

.

Die Registrierung mit Thin-Plate Splines kann aber, falls viele Kontrollpunkte benutzt werden, sehr zeitintensiv sein.

Elastische Modelle

Ein weiterer Ansatz für die Registrierung von Bildern, die sehr komplexe lokale Verzerrungen haben, ist die Registrierung mittels elastischer Modelle. Die Registrierung erfolgt hierbei meist iterativ durch die Minimierung eines Energiefunktionals, der Form

E(u)=D(u)+\alpha \langle Lu,u\rangle ,

mit dem Funktional $D$ , das die Ungleichheit der Bilder beschreibt, der Bilinearform $\langle Lu,u\rangle$ , die einen geeigneten Strafterm (auch Regularisierungsterm) beschreibt, und einem positiven Regularisierungsparameter $\alpha$ . Die Bilinearform ist häufig durch den elliptischen Operator

Lu=-\mu \Delta u-(\lambda +\mu )\nabla (\nabla u)

mit Neumann-Randbedingungen und den Elastizitätskonstanten $\lambda$ und $\mu$ gegeben. Die Registrierung funktioniert durch iterative Lösung der Euler-Lagrange-Gleichungen

{\frac {\partial E}{\partial u}}=\nabla D(u)+\alpha Lu=0

.

Hierdurch werden die Bilder als elastische Flächen oder zähe Flüssigkeiten modelliert, auf denen externe Kräfte $\nabla D(u)$ wirken und sie dadurch verformen. Die Verformung wird dabei durch die internen Kräfte $Lu$ beeinflusst und durch den Parameter $\alpha$ geeignet skaliert. Die Schritte der Merkmalsanpassung und Transformationsberechnung fallen hierbei zusammen.

Transformation

Die berechneten Transformationen werden nun benutzt, um das Objektbild zu transformieren und somit die Bilder zu registrieren. Die Transformation kann vorwärts oder rückwärts durchgeführt werden. Wird sie vorwärts durchgeführt, so wird für jeden Bildpunkt des Objektbildes mittels der Transformationsfunktionen eine neue Position berechnet. Dieses Vorgehen hat aber entscheidende Nachteile. Einerseits können mehrere Bildpunkte des Objektbildes auf ein und denselben neuen Bildpunkt transformiert werden und andererseits können im transformierten Bild Löcher entstehen. Ein Loch entsteht dann, wenn es im transformierten Bild einen Punkt (x, y) gibt, auf den kein Bildpunkt des Objektbildes transformiert wird.

Wird die Transformation rückwärts ausgeführt, dann wird der Intensitätswert an der Position (x, y) im transformierten Bild wie folgt berechnet. Zuerst wird ausgehend von der Position (x, y) mittels der inversen Transformation eine Gitterposition (x', y') im Objektbild berechnet. Dann wird der Intensitätswert im transformierten Bild durch Interpolation aus den (x', y') umgebenden Bildpunkten berechnet. Oft angewandte Interpolationstechniken sind dabei z. B. bilineare oder bikubische Interpolation. Auf diese Weise wird für jeden Bildpunkt des transformierten Bildes ein Intensitätswert berechnet.

Literatur

R. Bajcsy, S. Kovacic: Multiresolution elastic matching, Computer Vision, Graphics and Image Processing, Bd. 46, 1989, S. 1–21
Jan Modersitzki: Numerical Methods for Image Registration, Oxford University Press, 2004.
M. Bro-Nielsen, C. Gramkow: Fast fluid registration of medical images, in Visualization in Biomedical Computing. 4th International Conference, VBC '96 Proceedings, 1996, S. 267–276
F. L. Bookstein: Principal Warps: Thin Plate Splines and the Decomposition of Deformations, IEEE Transactions on Pattern Analysis and Machine Intelligence, Bd. 11, Nr. 6, 1989, S. 567–585
R. N. Bracewell: The Fourier Transform and Its Applications, McGraw-Hill, New York, 1965
L. G. Brown: A Survey of Image Registration Techniques, ACM Computing Surveys, Bd. 24, Nr. 4, 1992, S. 325–376
Stefan Henn, Florian Jarre und Kristian Witsch: Mathematische Bildverarbeitung – Ein Überblick über verschiedene Modelle und Methoden zur Registrierung digitaler Bilddaten, Jahrbuch der Heinrich-Heine-Universität Düsseldorf 2002, S. 178–188: http://dup.oa.hhu.de/64/1/pagesjarre.pdf
Stefan Henn, Kristian Witsch: Iterative Multigrid Regularization Techniques For Image Matching, SIAM Journal on Scientific Computing (SISC), 23(4) (2001), 1077–1093.
B. Zitova, J. Flusser: Image registration methods: a survey, Elsevier. Image and Vision Computing, Bd. 21, 2003, S. 977–1000
Boris Peter Selby, Georgios Sakas, Uwe Stilla et al. A Radiometry tolerant method for direct 3D/2D registration of computed tomography data to X-ray images: Transfer function independent registration. Bildverarbeitung für die Medizin (BVM) 2010: http://www.selbytec.de/publications/
A. Sotiras, C. Davatzikos, N. Paragios: Deformable Medical Image Registration: A Survey, IEEE Transactions on Medical Imaging, Bd. 32, Nr. 7, 2013, S. 1153–1190

Weblinks

Commons: Image registration – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.