Kanalkodierung

Als Kanalkodierung (auch Kanalcodierung) bezeichnet man in der Nachrichtentechnik das Verfahren, digitale Daten bei der Übertragung über gestörte Kanäle durch Hinzufügen von Redundanz gegen Übertragungsfehler zu schützen.

Die mathematischen Grundlagen für die Kanalkodierung stellt die Kodierungstheorie bereit.

Zu unterscheiden ist die Kanalkodierung von der Quellenkodierung, welche Redundanz vermindert, und von der Leitungskodierung, welche eine spektrale Anpassung an die Anforderungen des Übertragungskanals vornimmt.

Verfahren

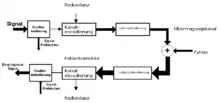
Übertragung mit Quellen-, Kanal- und Leitungskodierung

Die Kanalkodierung fügt den Daten am Eingang eines Übertragungskanals Redundanz hinzu und dekodiert die Daten an seinem Ausgang. Wenn die Zusatzinformationen lediglich auf einen Fehler hindeuten und eine Neuübertragung der Daten erfordern, spricht man von Rückwärtsfehlerkorrektur. Genügt die Redundanzinformation, den Fehler zu korrigieren, so handelt es sich um eine Vorwärtsfehlerkorrektur. Eine effiziente Kanalkodierung erhöht das Signal-Rausch-Verhältnis bei unveränderter Bitfehlerhäufigkeit. Je nach Kanalkodierungsverfahren beträgt der Codegewinn mehrere dB.

Eine wesentliche Eigenschaft eines Kanalkodes ist seine (Kode-) Coderate:

R=k/n

wobei

$k$ die Anzahl der Symbole am Eingang des Kodierers (Informationssymbole) ist und
$n$ die Anzahl der Symbole am Ausgang des Kodierers (Codesymbole).

Es werden also $k$ Informationssymbole auf $n$ Codesymbole abgebildet. Eine kleine Rate (großes $n$ ) bedeutet einen höheren Anteil der Codesymbole an den übertragenden Symbolen, also eine kleinere Datenübertragungsrate. Üblicherweise kann ein Kanalcode mit einer niedrigeren Koderate mehr Fehler korrigieren als ein vergleichbarer Kanalkode mit einer hohen Koderate – es ist also ein Abtausch zwischen Datenübertragungsrate und Fehlerkorrekturfähigkeit möglich.

Codeverkettung

Durch geschicktes Verketten von Codes (z. B. bei Turbo-Codes) kann die Korrekturfähigkeit des so entstandenen verketteten Codes sehr viel höher sein als die der einzelnen Codes (Komponentencodes).

Punktierung

Unter Punktierung versteht man das gezielte Streichen einzelner Codesymbole, so dass die Anzahl der übertragenden Codesymbole von $n$ auf $n'$ reduziert wird. Damit ergibt sich für den punktierten Code eine höhere Rate $R'=k/n'>k/n=R$ . Punktierung ermöglicht die Nutzung desselben Codierer/Decodierer-Paares für Codes unterschiedlicher Raten.

Geschichte

Shannons Pionierarbeit 1948

Die Veröffentlichung von Claude E. Shannons Pionierarbeit zur Informationstheorie A mathematical Theory of Communication stellt gleichzeitig die Geburtsstunde der Kanalkodierung 1948 dar. Zwar gab es vorher schon Bemühungen, Nachrichten gegen Fehlübertragung zu schützen, diese gingen jedoch nicht über eine einfache Mehrfachübertragung (Wiederholungscode) hinaus, was sich als ein Kanalcode ohne Codegewinn entpuppte. Shannon zeigte, dass jeder Übertragungskanal durch eine Kanalkapazität beschrieben werden kann, die die Informationsrate, die zuverlässig über einem Kanal erreicht werden kann, nach oben begrenzt. Zuverlässig heißt in diesem Zusammenhang, dass die Symbolfehlerrate nicht über einem festgelegten Grenzwert liegt. Er zeigte außerdem, dass Kanalcodes existieren, die beliebig nahe an diese Kapazität herankommen (Kanalkodierungstheorem). Der Existenzbeweis gibt jedoch weder eine praktische Konstruktion für Kanalcodes an, noch wie man diese effizient dekodiert. Tatsächlich sind die von Shannon beschriebenen Codes unendlich lang und haben einen zufälligen Charakter.[1]

Erste praktische Konstruktionen in den 1950er-Jahren

Bereits kurz nach Shannons Veröffentlichung wurden die ersten praktischen Kanalcodes entwickelt. Als besonders wegweisend sind hier die Arbeiten von Marcel J. E. Golay (Golay-Code, 1949)[2] und Richard W. Hamming (Hamming-Code, 1950). Hammings Arbeit wurde dabei von der Unzuverlässigkeit der damaligen Relais-Computer motiviert, in denen es häufig zu Bitfehlern kam. Der (7,4)-Hamming-Code kann mit nur 3 bit Redundanz einen beliebigen Bitfehler in 4 Nachrichtenbits korrigieren.[3]

Irving S. Reed und David E. Muller entwickelten 1954 die heute als Reed-Muller-Codes bekannten Kanalcodes. Reed-Muller-Codes haben den Vorteil, dass sie auch für große Blocklängen $n$ konstruiert werden können und dabei vergleichsweise viele Fehler korrigieren. Eine Unterklasse von Reed-Muller-Codes sind die Hadamard-Codes, die als erste Kanalcodes für die Datenübertragung von Raumsonden (Mariner-9) in die Geschichte eingingen.

1960er-Jahre: Algebraische Codes

Einen Meilenstein stellen die Reed-Solomon-Codes (nach Irving S. Reed und Gustave Solomon, 1960) und deren Untergruppe BCH-Codes (nach R. C. Bose, D. K. Ray-Chaudhuri und A. Hocquenghem) dar. Die Grundidee ist hier, Codesymbole aus einen endlichen Körper (anstatt Bits) zu verwenden, und Nachrichten als Polynome über diesem Körper zu betrachten, und Codeworte als Auswertung an der Polynome an $n$ verschiedenen Stellen. Dabei gelingt es, die Codeworte maximal voneinander zu separieren (Maximum Distance Separable Code, MDS-Code).[4] Reed-Solomon-Codes haben daher ausgezeichnete Fehlerkorrektureigenschaften und werden seitdem in vielen Anwendungen, wie CDs, DVDs, DVB und QR-Codes, eingesetzt. Ein effizienter Dekodierverfahren (Berlekamp-Massey-Algorithmus) wurde von Elvyn Berlekamp und James Massey zwischen 1968 und 1969 entwickelt.[5][6]

1970er- und 1980er-Jahre: Faltungscodes und Codeverkettung

Mit den Faltungscodes beschrieb Peter Elias bereits 1955 die ersten datenstrombasierten Codes, also Kanalcodes ohne eine festgelegte Blocklänge. Diese fanden jedoch erst mit dem effizienten Dekodieralgorithmus von Andrew Viterbi (Viterbi-Algorithmus, 1967) praktische Anwendung. Der Viterbi-Algorithmus erlaubte es erstmals, einfach eine sogenannte Soft-Input-Dekodierung anzuwenden, bei der (statt hart-entschiedenen Bitwerten) Wahrscheinlichkeiten für jedes Symbol berücksichtigt werden. Somit fanden Faltungscodes besonders Funkanwendungen wie GSM und WLAN (802.11a/g) Verwendung, bei denen diese Information zur Verfügung steht.[7] Dennoch ist deren Fehlerkorrekturfähigkeit von der Länge des verwendeten Schieberegisters abhängig, die exponentiell in die Dekodierkomplexität eingeht.

Serielle Codeverkettung (Dave Forney, 1966) erwies sich als Schlüsseltechnologie, um immer bessere Codes mit beherrschbarem Dekodieraufwand zu entwerfen. Dabei wird eine Nachricht zunächst mit einem (äußeren) Kanalcode (meist einem algebraischer Code) und anschließend mit einem (inneren) Faltungscode kodiert. Diese Methode fand 1977 mit den Voyager-Raumsonden eine prominente Anwendung und blieb das Zugpferd der Kanalkodierung bis zur Entwicklung der Turbo-Codes.

Iterative Dekodierung seit den 1990ern

Alle bisher genannten Kanalcodes operierten noch weit weg (d. h. mehrere Dezibel im Signal-Rausch-Verhältnis) von der von Shannon aufgezeigten Kanalkapazität, und es verbreitete sich die Ansicht, dass diese nicht auf praktikable Weise erreicht werden kann. Daher war die Aufruhr groß, als die Anfang den 1990er von Claude Berrou erfundenen Turbo-Codes (in der Veröffentlichung von 1993 sind Alain Glavieux und Punya Thitimajshima Mitautoren)[8] plötzlich diese Lücke zur Kanalkapazität bis auf einige Zehntel dB schlossen. In Turbo-Codes werden zwei parallel verkettete Faltungscodes mit einem pseudo-zufälligen Interleaver eingesetzt. Zum Dekodieren kommen zwei rückgekoppelte BCJR-Dekoder zum Einsatz – ein Prinzip, das an den Turbolader eines Verbrennungsmotors erinnert. In mehreren Iterationen tauschen beide Dekoder Information aus, um schließlich zu einem Codewort zu konvergieren. Es werden vergleichsweise kurze Schieberegister für die Faltungscodes verwendet, da bei Turbo-Codes der Interleaver dafür sorgt, dass die Codewortbits über die gesamte Länge des Codes miteinander verschränkt werden. Somit ist der Dekodieraufwand nur linear mit der Codewortlänge, was sehr lange Codes (viele Kilobit pro Codewort) erstmals praktikabel machte und damit den von Shannon erdachten Codes bereits sehr nahe kommt. Turbo-Codes fanden daraufhin Anwendung in den Mobilfunkstandards UMTS und LTE.[9]

Ähnlich gute Leistungsfähigkeit wie Turbo-Codes wies David J.C. MacKay 1996 bei LDPC-Codes nach, die mit dem Belief-Propagation-Algorithmus ebenfalls iterativ dekodiert werden[10]. Diese wurden zwar schon Anfang der 1960er von Robert Gallager erfunden[11], sie gerieten jedoch in Vergessenheit, da die damalige Technologie noch keine praktische Implementierung erlaubte. In den folgenden Jahren wurde in Arbeiten von Tom Richardson und Rüdiger Urbanke eine umfangreiche Theorie zur Konstruktion von LDPC-Codes entwickelt, sodass diese nun als Quasi-Stand der Technik in der Kanalkodierung gelten. Sie werden unter anderem im 5G-Mobilfunkstandard, neueren WLAN-Standards (802.11n und 802.11ac) und DVB-x2. In letzterem werden LDPC-Codes innere Codes mit BCH-Codes verkettet eingesetzt.

Polar Codes

Einen weiteren Fortschritt machte die Technik mit den 2008 von Erdal Arıkan eingeführten Polar-Codes. Er zeigte, dass Polar-Codes zusammen mit einem einfachen, rekursiven Dekodieralgorithmus, asymptotisch (also für eine Blocklänge, die gegen unendlich geht) die Kanalkapazität erreichen.[12] Damit sind Polar-Codes die ersten Codes, für die dies mathematisch nachgewiesen wurde, während die gute Leistungsfähigkeit von Turbo- und LDPC-Codes lediglich experimentell belegt ist. Für kurze Blocklängen sind Polar-Codes zwar anderen Schemen unterlegen, jedoch konnte durch Verkettung einer CRC-Prüfsumme eine ähnlich gute Leistungsfähigkeit wie bei kurzen LDPC-Codes erzielt werden. Daher wurden CRC-Polar-Codes für die Steuerkanäle in 5G-Mobilfunknetzen ausgewählt.[13]

Codeklassen

Kennt man die Fehlerarten, die in einem Übertragungskanal auftreten, kann man verschiedene Codes konstruieren, die die häufigen Fehlerarten gut, weniger häufigere Fehlerarten weniger gut korrigieren können. Die nebenstehende Abbildung zeigt eine Übersicht häufig verwendeter Codeklassen.

Übersicht häufig verwendeter Codeklassen

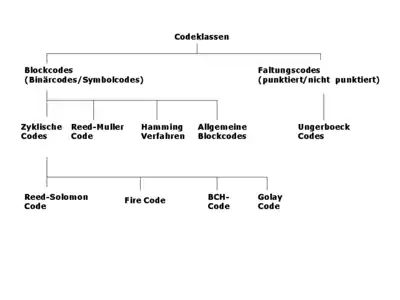
Grundsätzlich lassen sich Kanalcodes in blockbasierte und zeichenstrombasierte Codes unterteilen.

Blockbasierte Codes (Blockcodes)

Blockcodes zeichnen sich durch eine vordefinierte, konstante Codewortlänge $n$ aus.

Algebraische Codes

Algebraische Codes basieren auf algebraischen Konstruktionen. Sie werden entworfen, um ganz bestimmte Eigenschaften, beispielsweise eine große Minimaldistanz, zu erzielen. Daher lassen sich genaue Aussagen treffen, welche Fehlerarten und wie viele Fehler sie erkennen bzw. korrigieren können.

Paritätsbit

Codes für Iterative Dekodierung

Iterativ dekodierte Codes bezeichnet man auch als moderne Kanalcodes.[14] Im Gegensatz zu algebraischen Codes bestimmt hier der Dekodieralgorithmus den Code-Entwurf. Diese effizienten Algorithmen erlauben sehr lange Blocklängen, womit iterativ dekodierte Codes der Shannon-Kanalkapazität am nähesten kommen können. Sie zeichnen sich durch eine meist pseudo-zufällige Konstruktion aus. Die beiden wichtigsten Vertreter dieser Codeklasse sind:

Low-Density-Parity-Check-Code (LDPC Code)
Turbo-Code
- Turbo Convolutional Code (zwei terminierte Faltungscodes als Basiscodes)
- Turbo-Product-Code (beliebige algebraische Codes als Basiscodes)

Codes aus der Informationstheorie

Mit den 2008 eingeführten Polar-Codes wurden Blockcodes gefunden, die auf dem informationstheoretischen Prinzip der Kanal-Polarisierung basieren. Sie können keiner der beiden obigen Klassen zugeordnet werden, sind aber eng verwandt mit dem Reed-Muller-Code.

Polar-Code

Zeichenstrombasierte Codes

Im Gegensatz zu Blockcodes haben zeichenstrombasierte Codes keine festgelegte Blocklänge. Sie eignen sich daher für Streaming-Dienste und für Weitverkehrsnetze. Durch Terminierung können zeichenstrombasierte Codes in Blockcodes beliebiger Länge umgewandelt werden. Die wichtigsten Klassen zeichenstrombasierter Codes sind:

Faltungscodes
Ungerboeck-Code (auch als Trellis-Coded-Modulation bezeichnet)
Staircase Codes[15]
Räumlich verkettete LDPC-Codes (Spatially-Coupled LDPC-Codes, auch LDPC-Faltungscodes genannt)

Beispiele

Kanalfehler abhängig von Quellkodierung

Die Festlegung eines Kodierungsverfahren berücksichtigt sowohl die Qualitätsansprüche an das zu übertragende Signal als auch die Eigenschaften des Kanals. Wird beispielsweise bei einem unkomprimiert übertragenen Fernsehsignal ein Bit auf dem Übertragungsweg verfälscht, so ändert sich nur ein Pixel eines (Halb-)Bildes. Tritt der gleiche Fehler bei einem komprimierten MPEG-codierten Fernsehsignal auf, verfälscht er einen ganzen Makroblock von einer bestimmten Anzahl von Bildpunkten (je nachdem, wie groß der Makroblock ist: 16×16 bis hin zu 4×4 Pixel) und die darauffolgenden Bilder; erst wenn wieder ein unabhängig codiertes Frame (I-Frame) kommt, ist der Fehler nicht mehr vorhanden.

Beispiel Rückwärtsfehlerkorrektur

Hinzufügen von Paritätsbits zu einem Datenwort.

Beispiel Rückwärts-/Vorwärtsfehlerkorrektur

ISBN-Code: Bei fehlender Übereinstimmung mit der Prüfziffer kommen nur wenige ISBN-Codes als korrekte Werte in Frage.

Beispiel Vorwärtsfehlerkorrektur

Angabe von Postleitzahl und Ort: eine falsch geschriebene Ortsangabe kann anhand der Postleitzahl korrigiert werden. Ebenso werden Zahlendreher in der Postleitzahl durch den Abgleich mit dem Ortsnamen erkannt.

Beispiel GSM

Das Telefon begrenzt den Frequenzbereich der Sprache auf ca. 4 kHz. Bei einer Abtastung mit 8 kHz bei einer Quantisierung von 8 Bit pro Abtastwert fällt ein Datenstrom von 64 kbit/s an. Die GSM-Quellcodierung reduziert ihn auf ca. 13 kbit/s. Um die Bitfehlerhäufigkeit bei der störanfälligen Funkübertragung zu begrenzen, werden dem Datenstrom Redundanzen hinzugefügt. Die Kanalkodierung erhöht die Bitrate auf 22,8 kbit/s.

Siehe auch

Literatur

John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Prentice Hall, 2002, ISBN 0-13-095007-6.

Einzelnachweise

C. E. Shannon: A Mathematical Theory of Communication. In: Bell System Technical Journal. Band 27, Nr. 4, Oktober 1948, ISSN 0005-8580, S. 623–656, doi:10.1002/j.1538-7305.1948.tb00917.x.
Marcel Golay: Notes on Digital Coding. In: Proceedings of the IRE. Band 37, Nr. 6, Juni 1949, ISSN 0096-8390, S. 657–657, doi:10.1109/jrproc.1949.233620.
Hamming, R. W. (Richard Wesley), 1915–1998.: Coding and information theory. Prentice-Hall, Englewood Cliffs, N.J. 1980, ISBN 0-13-139139-9.
I. S. Reed, G. Solomon: Polynomial Codes Over Certain Finite Fields. In: Journal of the Society for Industrial and Applied Mathematics. Band 8, Nr. 2, Juni 1960, ISSN 0368-4245, S. 300–304, doi:10.1137/0108018.
E. Berlekamp: Nonbinary BCH decoding. In: IEEE Transactions on Information Theory. Band 14, Nr. 2, März 1968, ISSN 0018-9448, S. 242–242, doi:10.1109/tit.1968.1054109.
J. Massey: Shift-register synthesis and BCH decoding. In: IEEE Transactions on Information Theory. Band 15, Nr. 1, Januar 1969, ISSN 0018-9448, S. 122–127, doi:10.1109/tit.1969.1054260.
3rd Generation Partnership Project: "3GGP TS45.001: Technical Specification Group GSM/EDGE Radio Access Network; Physical layer on the radio path; General description".
C. Berrou, A. Glavieux, P. Thitimajshima: Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1. In: Proceedings of ICC '93 - IEEE International Conference on Communications. Band 2. IEEE, Geneva, Switzerland 1993, ISBN 978-0-7803-0950-0, S. 1064–1070, doi:10.1109/ICC.1993.397441 (ieee.org [abgerufen am 1. November 2020]).
3GPP: LTE; Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and channel coding (3GPP TS 36.212 version 10.0.0 Release 10). (etsi.org [PDF; abgerufen am 1. November 2020]).
D.J.C. MacKay, R.M. Neal: Near Shannon limit performance of low density parity check codes. In: Electronics Letters. Band 33, Nr. 6, 1997, ISSN 0013-5194, S. 457, doi:10.1049/el:19970362.
Robert G. Gallager: Low-Density Parity-Check Codes. The MIT Press, 1963, ISBN 978-0-262-25621-6.
Erdal Arikan: Channel polarization: A method for constructing capacity-achieving codes. In: 2008 IEEE International Symposium on Information Theory. IEEE, 2008, ISBN 978-1-4244-2256-2, doi:10.1109/isit.2008.4595172.
3GPP: 5G NR, 3GPP TS 38.212 version 15.2.0 Release 15: Multiplexing and Channel Coding. (etsi.org [PDF; abgerufen am 1. November 2020]).
Tom Richardson, Ruediger Urbanke: Modern Coding Theory. Cambridge University Press, Cambridge 2008, ISBN 978-0-511-79133-8.
Benjamin P. Smith, Arash Farhood, Andrew Hunt, Frank R. Kschischang, John Lodge: Staircase Codes: FEC for 100 Gb/s OTN. In: Journal of Lightwave Technology. Band 30, Nr. 1, Januar 2012, ISSN 0733-8724, S. 110–117, doi:10.1109/JLT.2011.2175479 (ieee.org [abgerufen am 2. November 2020]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] C. E. Shannon: A Mathematical Theory of Communication. In: Bell System Technical Journal. Band 27, Nr. 4, Oktober 1948, ISSN 0005-8580, S. 623–656, doi:10.1002/j.1538-7305.1948.tb00917.x.

[2] Marcel Golay: Notes on Digital Coding. In: Proceedings of the IRE. Band 37, Nr. 6, Juni 1949, ISSN 0096-8390, S. 657–657, doi:10.1109/jrproc.1949.233620.

[3] Hamming, R. W. (Richard Wesley), 1915–1998.: Coding and information theory. Prentice-Hall, Englewood Cliffs, N.J. 1980, ISBN 0-13-139139-9.

[4] I. S. Reed, G. Solomon: Polynomial Codes Over Certain Finite Fields. In: Journal of the Society for Industrial and Applied Mathematics. Band 8, Nr. 2, Juni 1960, ISSN 0368-4245, S. 300–304, doi:10.1137/0108018.

[5] E. Berlekamp: Nonbinary BCH decoding. In: IEEE Transactions on Information Theory. Band 14, Nr. 2, März 1968, ISSN 0018-9448, S. 242–242, doi:10.1109/tit.1968.1054109.

[6] J. Massey: Shift-register synthesis and BCH decoding. In: IEEE Transactions on Information Theory. Band 15, Nr. 1, Januar 1969, ISSN 0018-9448, S. 122–127, doi:10.1109/tit.1969.1054260.

[7] 3rd Generation Partnership Project: "3GGP TS45.001: Technical Specification Group GSM/EDGE Radio Access Network; Physical layer on the radio path; General description".

[8] C. Berrou, A. Glavieux, P. Thitimajshima: Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1. In: Proceedings of ICC '93 - IEEE International Conference on Communications. Band 2. IEEE, Geneva, Switzerland 1993, ISBN 978-0-7803-0950-0, S. 1064–1070, doi:10.1109/ICC.1993.397441 (ieee.org [abgerufen am 1. November 2020]).

[9] 3GPP: LTE; Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and channel coding (3GPP TS 36.212 version 10.0.0 Release 10). (etsi.org [PDF; abgerufen am 1. November 2020]).

[10] D.J.C. MacKay, R.M. Neal: Near Shannon limit performance of low density parity check codes. In: Electronics Letters. Band 33, Nr. 6, 1997, ISSN 0013-5194, S. 457, doi:10.1049/el:19970362.

[11] Robert G. Gallager: Low-Density Parity-Check Codes. The MIT Press, 1963, ISBN 978-0-262-25621-6.

[12] Erdal Arikan: Channel polarization: A method for constructing capacity-achieving codes. In: 2008 IEEE International Symposium on Information Theory. IEEE, 2008, ISBN 978-1-4244-2256-2, doi:10.1109/isit.2008.4595172.

[13] 3GPP: 5G NR, 3GPP TS 38.212 version 15.2.0 Release 15: Multiplexing and Channel Coding. (etsi.org [PDF; abgerufen am 1. November 2020]).

[14] Tom Richardson, Ruediger Urbanke: Modern Coding Theory. Cambridge University Press, Cambridge 2008, ISBN 978-0-511-79133-8.

[15] Benjamin P. Smith, Arash Farhood, Andrew Hunt, Frank R. Kschischang, John Lodge: Staircase Codes: FEC for 100 Gb/s OTN. In: Journal of Lightwave Technology. Band 30, Nr. 1, Januar 2012, ISSN 0733-8724, S. 110–117, doi:10.1109/JLT.2011.2175479 (ieee.org [abgerufen am 2. November 2020]).