Shannon-Fano-Kodierung
Die Shannon-Fano-Kodierung ist eine Entropiekodierung. Dabei kodiert man Zeichen entsprechend ihrer Auftrittshäufigkeit so, dass sie eine möglichst kleine mittlere Wortlänge besitzen. Durch die Entropie – der mittlere Informationsgehalt je Symbol – ist eine untere Schranke gegeben (Quellencodierungssatz).
Grundidee
Von der Entropiekodierung her ist bekannt, dass Zeichen mit einer unterschiedlichen Anzahl von Bits kodiert werden müssen, wenn man eine speichersparende Darstellung erhalten möchte. Es ist aber nicht möglich, den Zeichen einfach beliebige Bitfolgen zuzuweisen und diese auszugeben.
Wird zum Beispiel das Zeichen A mit der Bitfolge „10“, das Zeichen B mit der Folge „01“ und C mit „0“ kodiert, dann wird die Zeichenkette ABC zu „10010“. Diese Folge wird aber auch von der Zeichenkette „ACA“ erzeugt. Es ist also nicht mehr eindeutig erkennbar, für welche Zeichenfolge die Bitfolge „10010“ steht.
Um diese Mehrdeutigkeit zu verhindern, müssen[1] die den Zeichen zugewiesenen Bitfolgen präfixfrei sein, d. h. keine Bitfolge, die für ein einzelnes Zeichen steht, darf am Anfang eines anderen Zeichens stehen. Diese Eigenschaft ist im oberen Beispiel nicht erfüllt, da die Bitfolge „0“, die für C steht, am Anfang der B zugewiesenen Folge steht.

Die Grundidee ist, einen vollen binären Baum für die Darstellung des Codes zu verwenden. In dem Baum stehen die Blätter für die zu kodierenden Zeichen, während der Pfad von der Wurzel zum Blatt die Bitfolge bestimmt.
Das Bild zeigt einen Baum, der von der gewünschten Form ist. Die inneren Knoten sind durchnummeriert, um sie benennen zu können.
Um nun die Bitfolge zu ermitteln, die für eines der Zeichen stehen soll, muss festgelegt werden, wie die Abzweige kodiert werden sollen. Eine Variante ist, zu sagen, dass linke Teilbäume mit einer 0 und rechte mit einer 1 kodiert werden. Daraus folgen für den Beispielbaum folgende Bitfolgen:
| A | B | C | D | E |
|---|---|---|---|---|
| 00 | 01 | 100 | 101 | 11 |
Genauso gut sind aber auch viele andere Kodierungen möglich. Hier nur noch ein paar Beispiele:
| A | B | C | D | E |
|---|---|---|---|---|
| 10 | 11 | 000 | 001 | 01 |
| 11 | 10 | 010 | 011 | 00 |
| 11 | 10 | 001 | 000 | 01 |
Will man nun eine Zeichenfolge kodieren, so werden die den entsprechenden Zeichen zugewiesenen Bitfolgen hintereinander ausgegeben. Die Zeichenfolge „ACDC“ wird mit der ersten Kodierung zu der Bitfolge „00100101100“.
Um diese Bitfolge zu dekodieren, wird sie Bit für Bit abgearbeitet. Der Dekodierer muss sich dabei die aktuelle Position im Baum merken. Gestartet wird an der Wurzel, also im Knoten 1. Dann wird das erste Bit gelesen, eine 0. Das bedeutet bei dieser Kodierung nach links, der aktuelle Knoten wird also 2. Es folgt ein weiteres 0-Bit. Der aktuelle Knoten ist jetzt A. Es wird A ausgegeben und der aktuelle Knoten wieder auf 1 gesetzt. Das als nächstes gelesene 1-Bit führt dazu, dass der aktuelle Knoten die 3 ist usw.
Das nun zu lösende Problem ist es, einen solchen Baum zu erstellen, bei dem die durchschnittliche Anzahl der Fragen, bis ein Zeichen eindeutig ermittelt ist, im Mittel möglichst klein ist, also möglichst dicht an der Entropie liegt.
Shannon-Fano-Kodierung und Huffman-Kodierung sind zwei unterschiedliche Algorithmen zur Konstruktion dieser Bäume. Im Gegensatz zur Huffman-Kodierung ist die Shannon-Fano-Kodierung nicht immer optimal.
Shannon-Fano
Der nach Claude Shannon und Robert Fano benannte Algorithmus arbeitet mit folgender Vorschrift:
- Sortiere die Zeichen nach ihrer Häufigkeit.
- Teile die Zeichen entlang dieser Reihenfolge so in zwei Gruppen, dass die Summe der Häufigkeiten in den beiden Gruppen möglichst gleich ist. Die beiden Gruppen entsprechen dem linken und rechten Teilbaum des zu erstellenden Shannon-Baumes. Die dabei entstandene Partitionierung ist nicht unbedingt die beste, die mit den gegebenen Häufigkeiten zu erreichen ist. Die beste Partitionierung ist auch gar nicht gesucht, da diese nicht zwangsweise zu einem besseren Ergebnis führt. Worauf es ankommt ist, dass die mittlere Abweichung von der Entropie der Zeichen möglichst klein ist.
- Befindet sich mehr als ein Zeichen in einer der entstandenen Gruppen, wende den Algorithmus rekursiv auf diese Gruppe an.
Das wichtige Element an diesem Algorithmus ist der erste Schritt. Dieser sorgt dafür, dass Zeichen mit ähnlichen Wahrscheinlichkeiten oft im selben Teilbaum enden. Das ist wichtig, da Knoten im selben Baum Bitfolgen mit ähnlichen Codelängen erhalten (der maximale Unterschied kann nur die Anzahl der Knoten in diesem Baum betragen). Sind die Wahrscheinlichkeiten nun sehr unterschiedlich, kann man keine Bitfolgen mit den notwendigen Längenunterschieden erzeugen. Das führt dazu, dass seltene Zeichen zu kurze Bitfolgen und häufige Zeichen zu lange Bitfolgen erhalten.
Beispiel
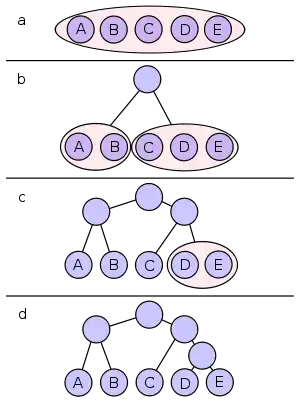
Das Beispiel zeigt die Konstruktion des Shannon-Codes für ein kleines Alphabet. Die fünf zu kodierenden Zeichen haben folgende Häufigkeiten:
| Zeichen | A | B | C | D | E |
|---|---|---|---|---|---|
| Häufigkeit | 15 | 7 | 6 | 6 | 5 |
Die Werte sind bereits sortiert, als nächstes folgt die Partitionierung. Am Anfang sind alle Zeichen in einer Partition (im Bild a).
Die Hälfte der Wahrscheinlichkeitssumme ist 19,5. 15 ist 4,5 unter diesem Halbwert, 15+7 hingegen nur 2,5 darüber – eine bessere Partitionierung gibt es nicht. Das Alphabet wird also so in 2 Teile unterteilt, dass der eine Teil die Zeichen A und B und der andere Teil den Rest (C, D und E) enthält (Bild b). Beide Partitionen enthalten noch mehr als 1 Zeichen, müssen also weiter zerteilt werden. Die Partition mit A und B kann nur in 2 Teile mit je einem Zeichen zerlegt werden. Die andere Gruppe hat 2 Möglichkeiten.
6+6 ist weiter von der Mitte entfernt, als 6 alleine. Also wird in die zwei Partitionen mit C und D+E unterteilt (Bild c). Schließlich wird noch D und E zerteilt. Der entstandene Entscheidungsbaum ist im Bild Abschnitt d dargestellt.
Den Zeichen A, B und C wurden also 2 Bits, D und E 3 Bits zugeordnet. Die Auftrittswahrscheinlichkeit von A beträgt 15/39, von B 7/39, von C sowie D 6/39 und von E 5/39. Somit ergibt sich für die mittlere Codewortlänge:
Da die Zuweisung nicht eindeutig ist, hier ein Beispiel für eine mögliche Kodierung aufgrund dieses Baumes:
| Zeichen | A | B | C | D | E |
|---|---|---|---|---|---|
| Kodierung | 00 | 01 | 10 | 110 | 111 |
Siehe auch
Einzelnachweise
- Tatsächlich müssen sie nur eindeutig sein, aber für jeden eindeutigen Code existiert auch ein präfixfreier Code mit identischer Codewortlänge