Atmosphärische Gegenstrahlung

Die atmosphärische Gegenstrahlung ist der Anteil der Wärmestrahlung aus der Atmosphäre, der in Richtung der Erde abgestrahlt wird und dessen Energie somit im System der Erde verbleibt. Sie ist ein wichtiger Bestandteil der Energiebilanz an der Oberfläche und trägt zum Treibhauseffekt bei. Sie heißt Gegenstrahlung, da sie dem Netto-Strahlungstransport von der Erde in das All entgegengesetzt ist und so die Strahlungsverluste der Erdoberfläche verringert.[2]

Beispiel einer Modellrechnung von 2009 zur mittleren jährlichen Strahlungsbilanz der Erde für den Zeitraum von März 2000 bis May 2004. Die Berechnungen wurden erstellt teils aufgrund von Satellitendaten (CERES) und teils aufgrund von Annahmen (Hypothesen). Die Breite der breiten Pfeile deutet die Proportionen des Energieflusses an.[1] Die Gegenstrahlung ist rechts unten dargestellt.

Je nach Teilgebiet der Physik ist die Größe Gegenstrahlung verschieden zu interpretieren:

In der quantenmechanischen Betrachtung bezeichnet sie die Wärmestrahlung vom kalten zum warmen Körper – untrennbar mit der intensiveren Strahlung in umgekehrter Richtung verbunden.
In der thermodynamischen Betrachtung bezeichnet die Gegenstrahlung einen der Terme in der Strahlungsbilanz, so dass alle Terme jeweils nur von der Temperatur eines der betrachteten Körper abhängen. Im idealisierten Treibhausmodell ist sie ein wesentlicher Bestandteil der Rechnung.

Beschreibung

Die von Treibhausgasen und Aerosolen in einem Volumenelement ausgehende Wärmestrahlung hängt von der lokalen Temperatur ab, siehe Stefan-Boltzmann-Gesetz, und von der spektralen Durchsichtigkeit, siehe unten. Die Strahlung wird isotrop (gleichförmig in alle Richtungen) abgestrahlt. Die den Boden erreichende Gegenstrahlung stammt für verschiedene Wellenlängen im Mittel aus verschiedenen Höhen und damit Temperaturbereichen. Im mittleren Infrarot kommt bei klarem Himmel ein größerer Anteil der Strahlung aus dem kalten Weltraum anstatt der Atmosphäre (siehe Atmosphärisches Fenster). In diesem Wellenlängenbereich transportiert daher die Gegenstrahlung besonders wenig Energie. Gerade in diesem Bereich liegt bei der Temperatur der Erdoberfläche das Strahlungsmaximum eines schwarzen Strahlers, der ein gutes Modell für den Erdboden ist. Er erhält daher weniger Wärmestrahlung aus der Atmosphäre als er ausstrahlt und kühlt nachts leicht unter die Temperatur der bodennahen Luft ab. Dann kann sich, abhängig von den Wetterverhältnissen, Tau, Reif oder Bodenfrost bilden.

Strahlungsquellen

Atmosphärengase

Die Hauptbestandteile der Luft (N₂, O₂, Ar) sind IR-inaktiv, werden also durch Wärmestrahlung weder angeregt noch emittieren sie solche. Verschiedene mehratomig aufgebaute Spurengase absorbieren und emittieren jedoch in charakteristischen Absorptionsbanden sehr intensiv und stellen damit Treibhausgase dar. Wasserdampf und Ozon sind gewinkelte Moleküle mit statischem Dipolmoment. Methan und Kohlendioxid besitzen aufgrund ihres symmetrischen Aufbaus kein statisches Dipolmoment, erhalten jedoch durch Schwingungsanregung ein Übergangsdipolmoment und emittieren daher.[3]

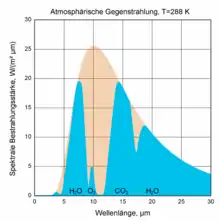
Spektrum der Gegenstrahlung (blau) bei klarem Himmel

Die hier betrachteten im langwelligen Infrarot gelegenen Spektrallinien entstehen nicht bei Übergängen zwischen verschiedenen Energieniveaus der Elektronenhülle, sondern bei Übergängen zwischen verschiedenen Rotations- oder Schwingungszuständen des Moleküls (siehe Molekularphysik). Solche Übergänge erzeugen typischerweise in einem begrenzten Wellenlängenbereich eine Vielzahl nahe beieinander liegender Spektrallinien; eine solche Ansammlung von Spektrallinien nennt man eine Spektralbande. Wasserdampf besitzt eine intensive Rotations-Schwingungs-Bande im Bereich von 5 bis 8 μm, während seine Rotationsbande die Wellenlängen oberhalb von 17 μm belegt. Kohlendioxid besitzt eine ebenfalls sehr intensive Bande zwischen 13 und 17 μm. Eine relativ schwache Bande des Ozons liegt bei 9,6 μm.[4]

Die nebenstehende Abbildung zeigt das beschriebene atmosphärische Bandenspektrum als Emissionsspektrum von Luft bei einer angenommenen Temperatur von 288 K (ca. 15 °C, globale Durchschnittstemperatur). Die hier schematisch als durchgehende Flächen (blau) dargestellten Banden bestehen in Wirklichkeit aus einer Vielzahl von eng aneinanderliegenden und einander teilweise überlappenden Spektrallinien. Der Vergleich mit dem Emissionsspektrum eines Schwarzen Körpers derselben Temperatur (hellbraun) zeigt, dass die Luft im Bereich der Banden fast so effizient emittiert wie der Schwarze Körper, in den Lücken zwischen den Banden jedoch so gut wie gar nicht. Insbesondere gibt es ein ausgeprägtes „Fenster“ im Bereich von etwa 8 bis 13 μm, in dem praktisch keine Emission stattfindet (außer der schwachen Ozonbande liegt im Fenster lediglich ein sehr schwaches Wasserdampfkontinuum; die schwachen Banden von Methan und Distickstoffmonoxid fallen in den Bereich zwischen 7 und 8 μm auf der Flanke der linken Wasserdampfbande[5]).

Die insgesamt von der Luft abgegebene thermische Strahlungsleistung ist daher geringer als die von einem Schwarzen Körper derselben Temperatur emittierte Leistung. Luft ist ein Wärmestrahler mit relativ geringer Effizienz.

Da wegen des kirchhoffschen Strahlungsgesetzes ein Strahler bei denjenigen Wellenlängen, bei denen er gut emittiert, auch gut absorbiert, stellt die Abbildung gleichzeitig das Absorptionsspektrum von Luft gegenüber thermischer Strahlung dar.

Darum durchlaufen die Emissionen der Gase nur eine kurze freie Weglänge, bevor sie von den Gasen wieder absorbiert und erneut emittiert werden. Die von höheren Luftschichten in Richtung Erdboden emittierte Strahlung wird nach kurzer Strecke von den tieferliegenden Luftschichten absorbiert und trägt zu deren Erwärmung bei, erreicht aber den Erdboden nicht. Dorthin gelangt sie erst nach mehreren Absorptions- und Reemissionszyklen. Die am Erdboden eintreffende Gegenstrahlung stammt bei klarem Himmel deshalb maximal aus einigen hundert Metern Höhe[6] und damit aus einer Luftschicht, in der sich die Temperatur nur geringfügig gegenüber dem bodennahen Wert ändert. Für die am Erdboden ankommende Strahlungsintensität ist daher im Wesentlichen die bodennahe Lufttemperatur maßgebend, wie etwa der von Wetterstationen standardgemäß in 2 m Höhe bestimmte Lufttemperatur-Messwert.

Aerosole

In der Atmosphäre enthaltene Aerosole (also Flüssigkeitströpfchen oder kleine Festkörper) senden keine Linienspektren, sondern kontinuierliche Spektren aus (vgl. das Schwarzkörperspektrum in obiger Abbildung) und strahlen daher auch in den von den Emissionslinien der Gase gelassenen Lücken des Spektrums. Sie können in hinreichender Konzentration die Gesamtstrahlung deutlich erhöhen und das Strahlungsdefizit gegenüber einem Schwarzen Körper stark vermindern (die Summe aus Atmosphären- und Aerosolstrahlung kann aber aus thermodynamischen Gründen bei keiner Wellenlänge stärker als die Strahlung eines Schwarzen Strahlers sein).

Von besonderer Bedeutung sind Wolken, deren Wassertröpfchen oder Eiskristalle praktisch Schwarze Strahler darstellen. Bei niedrig liegenden Wolken entspricht die Temperatur der Wolkenunterseite (Kondensationsniveau) in guter Näherung der von einer Wetterstation (üblicherweise in 2 m Höhe) gemessenen Taupunkttemperatur. Bei hinreichender Dicke der Bewölkungsschicht strahlen die Wolken als Schwarze Strahler mit dieser Temperatur. Aus diesem Grund kühlt die Erdoberfläche in bewölkten Nächten kaum ab – es herrscht ein Strahlungsgleichgewicht.

Messung

Ein Pyrgeometer zur Messung der Gegenstrahlung

Zur Messung der Gegenstrahlung eignen sich unter anderem so genannte Pyrgeometer: In einem Schutzgehäuse ist eine Thermosäule untergebracht, deren eines Ende (die Messfläche) geschwärzt und durch ein Fenster auf den Himmel ausgerichtet ist, während das andere Ende thermischen Kontakt mit dem Gehäuse hat. Das mit einem Interferenzfilter ausgestattete Fenster lässt nur Strahlung im Wellenlängenbereich von 5 bis 25 μm[7] passieren (insbesondere also keine Sonnenstrahlung). Die Messfläche gibt aufgrund ihrer Temperatur Wärmestrahlung gegen den Himmel ab und erhält von dort die Gegenstrahlung zugesandt. Je nach Bilanz zwischen aus- und eingehender Strahlung erwärmt sich die Messfläche oder kühlt sich ab. Die von der Thermosäule abgegebene Messspannung ist proportional zu dieser Temperaturänderung und erlaubt mittels eines geeigneten Kalibrierfaktors die momentane Strahlungsbilanz zu ermitteln (z. B. −35,4 W/m²). Mit der gleichzeitig separat gemessenen Gehäusetemperatur kann über das Stefan-Boltzmann-Gesetz die Eigenemission des Gerätes bestimmt werden. Da die gemessene Strahlungsbilanz die Differenz aus Gegenstrahlung und Eigenemission ist, lässt sich die Gegenstrahlung als Summe aus Strahlungsbilanz und Eigenemission ermitteln.

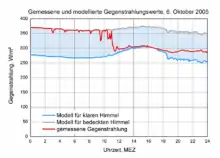
Verlauf der gemessenen Gegenstrahlung am 6. Oktober 2005

Die rote Kurve im nebenstehenden Diagramm zeigt den auf diese Weise von einer Wetterstation bei München gemessenen Verlauf der Gegenstrahlung am 6. Oktober 2005. Während des Vormittags herrschte Hochnebel. Die Nebeltröpfchen trugen als effiziente langwellige Strahler zu relativ hohen Strahlungswerten von ca. 370 W/m² bei. Gegen Mittag löste sich der Nebel auf und ließ einen klaren Himmel zurück. Die Atmosphärengase alleine sind weniger effiziente langwellige Strahler, die Strahlungswerte gingen daher merklich zurück, auf etwa 300 W/m². Die graue und die blaue Kurve wurden zum Vergleich für bedeckten bzw. klaren Himmel mittels empirischer Strahlungsmodelle (siehe unten) aus den gleichzeitig gemessenen Temperaturen und Luftfeuchten berechnet.

Die im Laufe eines Jahres an einem typischen Standort in Mitteleuropa anzutreffende Variationsbreite der Gegenstrahlungsintensität reicht von unter 200 W/m² in klaren Winternächten bis deutlich über 400 W/m² an bedeckten Sommertagen.[8] Über das Jahr und den ganzen Globus gemittelt beträgt die Intensität der Gegenstrahlung etwa 300 W/m².[9] Im Vergleich dazu erreicht die langwellige Abstrahlung der Erdoberfläche im globalen Mittel (unter Annahme einer mittleren Temperatur von ca. 288 K) etwa 373 W/m², so dass der Erdboden im Mittel einem Verlust von etwa 70 W/m² infolge langwelliger Abstrahlung unterliegt.[9]

Eine Messung von u. a. der atmosphärischen Gegenstrahlung findet z. B. an den 50 Stationen des World Radiation Monitoring Center statt.

Rechnerische Modellierung

Da die Strahlungsmechanismen bekannten physikalischen Gesetzmäßigkeiten unterliegen und die Strahlungseigenschaften der Treibhausgase gut erforscht sind, kann die Gegenstrahlungsintensität im Prinzip anstelle von direkten Messungen auch durch Modellrechnungen ermittelt werden, sofern der Zustand der Atmosphäre hinreichend genau bekannt ist. Kennt man beispielsweise den Atmosphärenzustand in verschiedenen Höhen, so lässt sich die Gegenstrahlung in Bodennähe recht genau durch Rechenmethoden bestimmen, welche den Strahlungstransport in der gleichzeitig emittierenden und absorbierenden Atmosphäre beschreiben. Der zur Erlangung der Atmosphärendaten erforderliche Aufwand (z. B. Radiosondenaufstiege) setzt dem Vorteil der Methode allerdings Grenzen.

Wegen der kurzen Reichweite der langwelligen Strahlung in der Atmosphäre stammt die am Erdboden eintreffende Gegenstrahlung maximal aus ein paar hundert Metern Höhe (siehe oben), so dass eine gute Abschätzung der Strahlungsintensität bereits bei Kenntnis des bodennahen Atmosphärenzustands möglich ist. Hierzu wurden verschiedene empirische Formeln entwickelt. Die Haupteinflussgröße ist die Temperatur. Hier steht meist die von Wetterstationen in 2 m Höhe gemessene Lufttemperatur zur Verfügung. Die Änderung der Temperatur über den relevanten Höhenbereich ist gering und kann durch geeignete empirische Formelparameter berücksichtigt werden. Die Konzentrationen der meisten Treibhausgase sind mehr oder weniger konstant und können ebenfalls über feste Parameter erfasst werden. Lediglich der Wasserdampfgehalt ist stark variabel, weshalb einige Formeln die Luftfeuchtigkeit als Eingangsvariable berücksichtigen. Zu dem auf diese Weise abschätzbaren Strahlungsanteil des klaren Himmels kommt gegebenenfalls der zusätzliche Beitrag von Bewölkung.

Die Gegenstrahlung bei wolkenlosem Himmel lässt sich beispielsweise über die Ångström-Formel abschätzen:[10][11]

A_{\mathrm {g,k} }\,=\,\sigma \,T_{\mathrm {St} }^{4}\,(0{,}790-0{,}174\cdot 10^{-0{,}041\mathrm {hPa} ^{-1}\cdot e})

Bei vollständig bewölktem Himmel und niedrig liegenden Wolken entspricht die Temperatur der Wolkenunterseite (Kondensationsniveau) in guter Näherung der von einer Wetterstation (üblicherweise in 2 m Höhe) gemessenen Taupunkttemperatur. Die Wolken emittieren als Schwarze Strahler mit dieser Temperatur:[11]

A_{\mathrm {g,w} }\,=\,\sigma \,T_{\mathrm {d,St} }^{4}

Die Gegenstrahlung eines teilweise bewölkten Himmels setzt sich anteilig zusammen aus den Beiträgen der Wolkenunterseiten und der klaren Himmelsflächen:

A_{\mathrm {g} }\,=\,N\cdot A_{\mathrm {g,w} }+(1-N)\cdot A_{\mathrm {g,k} }

mit:

$A_{\mathrm {g} }$ : atmosphärische Gegenstrahlung
$A_{\mathrm {g,k} }$ : atmosphärische Gegenstrahlung bei wolkenlosem Himmel
$A_{\mathrm {g,w} }$ : atmosphärische Gegenstrahlung bei bedecktem Himmel
$\sigma$ : Stefan-Boltzmann-Konstante
$T_{\mathrm {St} }$ : Stationstemperatur (in 2 m Höhe)
$T_{\mathrm {d,St} }$ : Taupunkttemperatur in Stationshöhe
$e$ : Wasserdampfpartialdruck an der Station
$N$ : Bedeckungsgrad

Die mit diesen Formeln aus Lufttemperatur und Luftfeuchte berechneten Gegenstrahlungswerte für einen vollständig klaren und einen vollständig bedeckten Himmel sind zum Vergleich mit den Messwerten in das Diagramm des vorhergehenden Abschnitts eingezeichnet (blaue bzw. graue Kurve). Wie zu erkennen ist, stimmt die Messkurve während des bewölkten Vormittags gut mit den für bewölkten Himmel berechneten Werten und nach dem Aufklaren gut mit den für klaren Himmel berechneten Werten überein. Am Abend nahm die Bewölkung offenbar wieder zu.

Strahlungsbilanz

Nachts bei klarem Himmel

Bei klarem Himmel besteht die Gegenstrahlung hauptsächlich aus der Wärmestrahlung der Atmosphärengase. Die für die Emission maßgebliche Temperatur ist praktisch identisch mit der bodennahen Lufttemperatur und damit ähnlich der Temperatur des ebenfalls abstrahlenden Erdbodens. Der Erdboden emittiert jedoch praktisch als Schwarzer Strahler, während die Intensität der atmosphärischen Strahlung wegen der Lücken im Emissionsspektrum trotz ähnlicher Temperatur deutlich geringer ist.

Die terrestrische Ausstrahlung kann daher durch die atmosphärische Gegenstrahlung nur teilweise kompensiert werden und die Erdoberfläche kühlt ab: klare Nächte sind besonders kühl. Die Erdoberfläche und andere terrestrische Oberflächen (Hausdächer, Hausfassaden, Autoscheiben etc.) können dabei nicht nur unter die Lufttemperatur, sondern sogar unter die Taupunkttemperatur abkühlen. Folge dieser nächtlichen Unterkühlung sind dann Tauwasserausfall und im Winter Reifbildung.

Im Wüstenklima enthält die Luft nur noch geringe Spuren des Treibhausgases Wasserdampf; die Gegenstrahlung hat besonders geringe Intensität und Wüstennächte sind sehr kalt.

Die an Fernrohren angebrachten Taukappen haben den Zweck, den Strahlungsverlust und damit die Unterkühlung der Objektivlinse zu verringern, indem sie einen Teil des Himmels im Gesichtsfeld der Linse abdecken. Aus diesem Bereich des Himmels erhält die Linse Strahlung von der gut abstrahlenden Taukappe anstelle der geringeren Strahlung aus der fast gleich warmen aber weniger gut strahlenden Atmosphäre.

Nachts bei bedecktem Himmel

Bei bedecktem Himmel ist die Gegenstrahlung wegen des Beitrags der Wolken merklich intensiver. Da in gemäßigten Breiten nachts die relative Feuchte im Mittel etwa 80 % und mehr beträgt, liegt die für die Gegenstrahlung der Bewölkung maßgebliche Taupunkttemperatur nur knapp unter der Lufttemperatur.

Dem Erdboden, der ebenfalls ungefähr Lufttemperatur hat, stehen nun gut strahlende Wolken ähnlicher Temperatur gegenüber. Die Strahlungsbilanz ist fast ausgeglichen und die Erdoberfläche kühlt nur wenig ab: Bedeckte Nächte sind wärmer, es fällt nur wenig oder gar kein Tau aus.

Tagsüber

Tagsüber liegt dieselbe je nach Bewölkungsgrad mehr oder weniger unausgeglichene Bilanz von terrestrischer Ausstrahlung und atmosphärischer Gegenstrahlung vor. Die während des Tages zusätzlich einfallende kurzwellige Sonnenstrahlung wird jedoch überwiegend vom Erdboden und weit weniger von der Atmosphäre absorbiert, so dass die Erdoberflächentemperatur über die Lufttemperatur steigt. Die gesamte lang- und kurzwellige Strahlungsbilanz ist für den Erdboden nun positiv.

Beispiel

Bereifte Grashalme

Mit Gegenstrahlung ist die nachfolgend beschriebene Erscheinung ein seltenes Ereignis. Ohne die Existenz der Gegenstrahlung (oder die gleichwertige Betrachtungsweise, dass der Wärmestrom von einem warmen zum kühleren Körper auch von der Temperatur des kühleren Körpers abhängt) würde die nachfolgend beschriebene Erscheinung fast jede Nacht eintreten.

Man betrachte einen Grashalm in einer klaren windstillen Herbstnacht. Die Lufttemperatur betrage +5 °C, die Luftfeuchte 90 %, der konvektive Wärmeübergangskoeffizient 5 W/m²K, der Emissionsgrad des Grases 0,95. Die Unterseite des Halms stehe mit darunterliegenden Halmen derselben Temperatur im Strahlungsgleichgewicht, die Oberseite strahle gegen den klaren Himmel ab. Sie gewinnt die atmosphärische Gegenstrahlung sowie den konvektiven Wärmestrom aus der Umgebungsluft und verliert ihre thermische Eigenemission gemäß dem Stefan-Boltzmann-Gesetz. Ihre Energiebilanz lautet also:

E\,=\,\varepsilon \,A_{\mathrm {g,k} }+\alpha _{k}(\vartheta _{\mathrm {L} }-\vartheta _{\mathrm {O} })-\varepsilon \,\sigma \,\vartheta _{\mathrm {O} }^{4}

mit

$\,E$	Energiebilanz, W/m²
$\,A_{\mathrm {g,k} }$	atmosphärische Gegenstrahlung bei wolkenlosem Himmel, W/m²
$\,\alpha _{k}$	konvektiver Wärmeübergangskoeffizient, W/m²K
$\,\varepsilon$	Emissionsgrad der Oberfläche, 0…1
$\,\vartheta _{\mathrm {L} }$	Lufttemperatur, K
$\,\vartheta _{\mathrm {O} }$	Oberflächentemperatur, K

Unter den gegebenen Bedingungen beträgt der Wasserdampfpartialdruck 7,85 hPa, die atmosphärische Gegenstrahlung also 240 W/m². Die thermische Emission der anfangs auf 5 °C befindlichen Oberfläche beläuft sich zunächst auf 322 W/m². Da die Oberfläche mehr Wärme verliert als gewinnt, kühlt sie ab. Dabei nehmen die Emissionsverluste wegen der fallenden Temperatur ab, während der konvektive Wärmezustrom wegen der anwachsenden Temperaturdifferenz zwischen Oberfläche und Luft zunimmt. Sobald sich thermisches Gleichgewicht eingestellt hat, ist die Energiebilanz Null (Verluste und Gewinne heben sich auf) und Lösen der Bilanzgleichung liefert die Oberflächentemperatur $\vartheta _{\mathrm {O} }=-5{,}1\,^{\circ }\mathrm {C}$ .

Der Grashalm unterkühlt also merklich unter die Lufttemperatur. Er unterschreitet nicht nur die Taupunkttemperatur der Luft (+3,5 °C), so dass Tau ausfällt, er unterschreitet auch den Gefrierpunkt, so dass sich der Tau als Reif niederschlägt (bei fortdauerndem Bereifen wäre die freiwerdende Latentwärme in der Energiebilanz zu berücksichtigen). Es tritt Bodenfrost (konkret Strahlungsfrost) auf, obwohl die Lufttemperatur deutlich über dem Gefrierpunkt liegt.

In der Praxis fällt die Unterkühlung meist geringer aus als in diesem vereinfachten Beispiel. Die Wärmekapazität einer thermisch trägeren Oberfläche, tagsüber aufgenommene Wärmereserven sowie infolge Tau- oder Reifbildung frei werdende Latentwärme können die Abkühlung verzögern. Wind verstärkt die konvektive Wärmezufuhr und verringert die Unterkühlung. Insbesondere können die Strahlungsverluste der abstrahlenden Oberfläche vermindert werden, wenn sich in ihrem Gesichtsfeld terrestrische Objekte befinden. Solche Objekte geben allein aufgrund ihrer besseren Strahlungseigenschaften mehr Strahlung (terrestrische Gegenstrahlung) ab als die Luft, selbst wenn sie nicht wärmer als die Luft sind. Pflanzen können durch Bedecken mit einer Plane vor Strahlungsfrost bewahrt werden, weil die Plane (obwohl sie selbst nur Lufttemperatur hat) stärker strahlt als die Luft. Pflanzen, die an einen „geschützten“ Platz in einer Mauerecke gestellt werden, sehen weniger Himmel und verlieren weniger Wärmestrahlung.

Das Beispiel illustriert die mikroklimatischen Folgen des Umstandes, dass die Luft ein relativ schlechter Wärmestrahler ist. Andererseits hat die Tatsache, dass die Luft überhaupt Wärmestrahlung abgibt, erhebliche makroklimatische Folgen. Wiederholt man die obige Rechnung für den hypothetischen Fall $A_{\mathrm {g,k} }=0$ , so erhält man eine Abkühlung der jetzt unkompensiert abstrahlenden Oberfläche auf −32 °C. Eine solch ausgeprägte nächtliche Unterkühlung unter die Lufttemperatur widerspräche jeglicher Alltagserfahrung. Die wärmende Wirkung der atmosphärischen Gegenstrahlung ist demnach von erheblicher Bedeutung. Man bezeichnet diese Wirkung als den natürlichen atmosphärischen Treibhauseffekt.

Treibhauseffekt

Hauptartikel: Treibhauseffekt

Die Erdoberfläche absorbiert im globalen und langfristigen Mittel etwa 175 W/m² an Sonnenstrahlung.[9] Da sich die Erde – von klimatologischen Schwankungen abgesehen – langfristig weder erheblich erwärmt noch abkühlt, befindet sie sich offenbar im Strahlungsgleichgewicht mit der Sonne und muss im Mittel einen Wärmestrom desselben Betrags abgeben. Die mittlere Temperatur der Erdoberfläche beträgt etwa 288 K.[9] Betrachtet man die Erde in freilich erheblicher Vereinfachung als Kugel mit einheitlicher Oberflächentemperatur, so strahlt sie nach dem Stefan-Boltzmann-Gesetz (bei 288 K und angenommenem Emissionsgrad 0,95) eine Wärmeleistung von 373 W/m²[9] ab, was deutlich über der Zustrahlung liegt und das Strahlungsgleichgewicht zu verletzen scheint.

Die Diskrepanz löst sich auf, wenn der Strahlungsbeitrag der Atmosphäre berücksichtigt wird. Der Erdboden empfängt im Mittel nicht nur 175 W/m² an Sonnenstrahlung, sondern auch 300 W/m² an Gegenstrahlung.[9] Bei insgesamt 475 W/m² Strahlungsgewinn und 373 W/m² Strahlungsverlust verbleibt dem Erdboden ein Wärmegewinn von etwa 100 W/m², den er über Konvektion und Verdunstung an die Atmosphäre abgibt. Die Energiebilanz der Erdoberfläche bleibt also dank der atmosphärischen Gegenstrahlung trotz der relativ hohen Oberflächentemperatur gewahrt.

Der Erdboden erhält im globalen Mittel aus der Atmosphäre knapp doppelt so viel Wärmestrahlung (300 W/m²) wie von der Sonne (175 W/m²). Gäbe es diese Zustrahlung der Atmosphäre nicht, so würde die Energiebilanz nur eine erheblich geringere Wärmeabstrahlung und damit eine geringere Erdoberflächentemperatur zulassen. Die übliche Überschlagsrechnung setzt die von Erdboden und Atmosphäre absorbierten solaren Wärmegewinne an (bei einer planetaren Albedo von 30 % insgesamt etwa 240 W/m²) und findet, dass sie ohne Treibhauseffekt mit der Wärmeabstrahlung bei −15 °C (angenommener Emissionsgrad 0,95) oder −18 °C (Emissionsgrad 1,0) im Gleichgewicht stehen.[9] Die 30 K Temperaturunterschied zu den tatsächlichen Verhältnissen werden dem Treibhauseffekt zugeschrieben.

Die Situation eines Planeten mit Atmosphäre aber ohne Treibhauseffekt ist zu unterscheiden von der Situation ohne Atmosphäre, wie sie beispielsweise beim Mond vorzufinden ist. Eine Atmosphäre streut einen Teil des Lichts zurück in den Weltraum, damit erhöht sich die Albedo im Vergleich zu einem Körper ohne Atmosphäre. Der absorptionsbedingte solare Wärmegewinn des fast ausschließlich von Direktstrahlung getroffenen Bodens ist ohne Atmosphäre höher. Für eine Oberflächenalbedo von 10 % ergeben sich mittlere Oberflächentemperaturen von 0 °C (Emissionsgrad 0,95) bzw. −3 °C (Emissionsgrad 1).[9] Eine Atmosphäre, und in noch größerem Ausmaß eine Bewölkung, verringert zwar durch eine erhöhte Albedo den Anteil der Direktstrahlung, erhöht aber durch die damit verbundene Gegenstrahlung die einfallende Strahlungsleistung in Bodennähe und damit die Bodentemperatur, weil der Boden dann nur durch eine höhere Temperatur eine ausgeglichene Strahlungsbilanz erreichen kann. Neben den Effekten von Albedo und Gegenstrahlung wirkt eine Atmosphäre darüber hinaus auch ausgleichend auf Temperaturverlauf und regionale Temperaturverteilung: Winde transportieren Energie (meist polwärts) und die Wärmekapazität der Atmosphäre verringert den Temperaturunterschied zwischen Tag- und Nachttemperaturen.

Der soeben beschriebene Treibhauseffekt ist eine natürliche Konsequenz der atmosphärischen Eigenschaften und mit seinen Auswirkungen auf die Temperaturverhältnisse der Erde eine wesentliche Voraussetzung für die Entwicklung der Biosphäre. Änderungen des Treibhauseffekts sind Teil der als Strahlungsantrieb zusammengefassten Änderungen des Strahlungshaushalts gegenüber dem Referenzjahr 1750.

Literatur

S. Arrhenius (1896): On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground. In: Philosophical Magazine and Journal of Science 41, Nr. 251, 1896, S. 237–276 (PDF (Memento vom 6. Oktober 2014 im Internet Archive) 4,1 MB; die erste quantitative Untersuchung des Beitrags von Kohlendioxid zum Treibhauseffekt).
K. Blümel et al.: Entwicklung von Testreferenzjahren (TRY) für Klimaregionen der Bundesrepublik Deutschland. BMFT, Forschungsbericht T 86-051, 1986.
R. Geiger, R. H. Aron, P. Todhunter: The Climate Near the Ground. 5. Auflage, Vieweg, Braunschweig 1995, ISBN 3-528-08948-2.
H. Häckel: Meteorologie. Ulmer, Stuttgart 1999, ISBN 3-8001-2728-8.
M.G. Iziomon, H. Mayer, A. Matzarakis: Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. Journal of Atmospheric and Solar-Terrestrial Physics 65 (2003), S. 1107–1116 (PDF (Memento vom 12. Januar 2006 im Internet Archive), 325 kB).
G. H. Liljequist, K. Cehak: Allgemeine Meteorologie. 3. Auflage, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig/Wiesbaden 1984, ISBN 3-540-41565-3.
H. Malberg: Meteorologie und Klimatologie. Eine Einführung. 4. Auflage, Springer-Verlag, Berlin/Heidelberg/New York 2002, ISBN 3-540-42919-0.
F. Möller: Einführung in die Meteorologie. Band 2: Physik der Atmosphäre. Bibliographisches Institut, Mannheim 1973, ISBN 3-411-00288-3.
W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 3. Auflage. Springer, Berlin/Heidelberg 2000, ISBN 3-540-67180-3, 1.3 Terrestrische Strahlung, S. 38–41.
U. Wolfseher: Der Wärmetransport an Bauteiloberflächen unter besonderer Berücksichtigung des langwelligen Strahlungsaustausches. Gesundheits-Ingenieur – Haustechnik – Bauphysik – Umwelttechnik 102 (1981) Heft 4, S. 184–200.

Weblinks

Earth’s radiation budget and Greenhouse Effect, archive.org Memento vom 28. Dez. 2010

Einzelnachweise

Kevin E. Trenberth, John T. Fasullo, Jeffrey Kiehl: Earth's Global Energy Budget. In: Bulletin of the American Meteorological Society. Band 90, Nr. 3, 2009, S. 311–324, doi:10.1175/2008BAMS2634.1., Fig. 1, S. 314.
R. Geiger, R.H. Aron, P. Todhunter: The Climate Near the Ground. 5th ed., Vieweg, Braunschweig 1995, ISBN 3-528-08948-2, S. 11: „Longwave radiation emitted by the atmosphere G is termed counterradiation (sometimes called longwave irradiance or atmospheric radiation) since it counteracts the terrestrial radiation loss from the surface.“
Vorlesungsmaterial von Prof. W. de Boer von der Universität Karlsruhe zum Thema Rotation und Vibration von Molekülen (SS 2005) (Memento vom 21. Juni 2007 im Internet Archive)
F. Möller: Einführung in die Meteorologie. Band 2: Physik der Atmosphäre. Bibliographisches Institut, Mannheim 1973, ISBN 3-411-00288-3, S. 51.
W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 2. Auflage, Springer, Berlin 1994, ISBN 3-540-57885-4, S. 40.
R. Geiger, R. H. Aron, P. Todhunter: The Climate Near the Ground. 5. Auflage, Vieweg, Braunschweig 1995, ISBN 3-528-08948-2, S. 21.
Kipp & Zonen (Hrsg.): Instruction Manual CG1/CG2 Pyrgeometer / Net Pyrgeometer. Delft 1992.
H. Häckel: Meteorologie. Ulmer, Stuttgart 1999, ISBN 3-8001-2728-8, S. 184, Tab. 14.
W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 2. Auflage, Springer, Berlin 1994, ISBN 3-540-57885-4, S. 37f.
F. Möller: Einführung in die Meteorologie. Band 2: Physik der Atmosphäre. Bibliographisches Institut, Mannheim 1973, ISBN 3-411-00288-3, S. 53.
K. Blümel et al.: Entwicklung von Testreferenzjahren (TRY) für Klimaregionen der Bundesrepublik Deutschland. BMFT, Forschungsbericht T 86-051, 1986, S. 73 (unter Korrektur eines Vorzeichenfehlers).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Kevin E. Trenberth, John T. Fasullo, Jeffrey Kiehl: Earth's Global Energy Budget. In: Bulletin of the American Meteorological Society. Band 90, Nr. 3, 2009, S. 311–324, doi:10.1175/2008BAMS2634.1., Fig. 1, S. 314.

[2] R. Geiger, R.H. Aron, P. Todhunter: The Climate Near the Ground. 5th ed., Vieweg, Braunschweig 1995, ISBN 3-528-08948-2, S. 11: „Longwave radiation emitted by the atmosphere G is termed counterradiation (sometimes called longwave irradiance or atmospheric radiation) since it counteracts the terrestrial radiation loss from the surface.“

[3] Vorlesungsmaterial von Prof. W. de Boer von der Universität Karlsruhe zum Thema Rotation und Vibration von Molekülen (SS 2005) (Memento vom 21. Juni 2007 im Internet Archive)

[MoellerS51-4] F. Möller: Einführung in die Meteorologie. Band 2: Physik der Atmosphäre. Bibliographisches Institut, Mannheim 1973, ISBN 3-411-00288-3, S. 51.

[5] W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 2. Auflage, Springer, Berlin 1994, ISBN 3-540-57885-4, S. 40.

[6] R. Geiger, R. H. Aron, P. Todhunter: The Climate Near the Ground. 5. Auflage, Vieweg, Braunschweig 1995, ISBN 3-528-08948-2, S. 21.

[7] Kipp & Zonen (Hrsg.): Instruction Manual CG1/CG2 Pyrgeometer / Net Pyrgeometer. Delft 1992.

[8] H. Häckel: Meteorologie. Ulmer, Stuttgart 1999, ISBN 3-8001-2728-8, S. 184, Tab. 14.

[RoedelS37-9] W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 2. Auflage, Springer, Berlin 1994, ISBN 3-540-57885-4, S. 37f.

[MoellerS53-10] F. Möller: Einführung in die Meteorologie. Band 2: Physik der Atmosphäre. Bibliographisches Institut, Mannheim 1973, ISBN 3-411-00288-3, S. 53.

[Blümel_1986_73-11] K. Blümel et al.: Entwicklung von Testreferenzjahren (TRY) für Klimaregionen der Bundesrepublik Deutschland. BMFT, Forschungsbericht T 86-051, 1986, S. 73 (unter Korrektur eines Vorzeichenfehlers).