Idealisiertes Treibhausmodell

Das idealisierte Treibhausmodell ist ein einfaches Modell zur Bestimmung der Oberflächen- und der Atmosphärentemperatur der Erde oder eines anderen Planeten. Mit Hilfe eines idealisierten Planeten kann der Treibhauseffekt illustriert werden; dieses Modell ist üblich in entsprechenden Lehrbüchern.[1]

Überblick

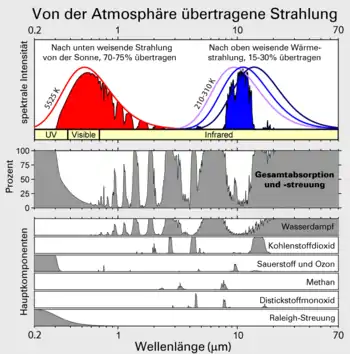
Zentrale Bedingung des Treibhauseffekts, dargestellt am Beispiel des Planeten Erde: Die Wellenlängenverteilung der von der Sonne kommenden Strahlung unterscheidet sich von der Infrarotstrahlung, wie sie von der Erde abgestrahlt wird (hier exemplarisch für drei Temperaturwerte der Erde). Darunter ist dargestellt, welche Teile der Atmosphäre welchen spektralen Bereich herausfiltern.

Die Oberfläche der Sonne strahlt elektromagnetische Wellen im sichtbaren Bereich und darüber hinaus, etwas als Wärmestrahlung, ab. Die Strahlung entspricht der eines Körpers einer effektiven Temperatur von ca. 5.500 °C. Die Erde ist erheblich kälter und strahlt – wie es das plancksche Strahlungsgesetz beschreibt – bei erheblich längeren Wellenlängen, vor allem im Infrarotbereich. Das idealisierte Treibhausmodell fußt darauf, dass bestimmte Gase der Erdatmosphäre für kurzwellige elektromagnetische Sonnenstrahlen (wie z. B. sichtbares Licht) transparent, für die von der Erdoberfläche emittierte langwellige Wärmestrahlung jedoch wenig durchlässig sind. Zu diesen Gasen zählen z. B. Kohlenstoffdioxid und Wasserdampf. Wärme kann also leicht in die Atmosphäre eindringen, wird dort aber teilweise festgehalten. Das beeinflusst den Strahlungshaushalt der Erde nachhaltig.

Das Kirchhoffsche Strahlungsgesetz besagt, dass jeder Körper, der sich im thermischen Gleichgewicht befindet, die von ihm absorbierte Energie wieder emittieren muss. Ein isotroper Körper strahlt in alle Richtungen gleichermaßen. Folglich strahlt die Atmosphäre im langwelligen Infrarotbereich auch in Richtung Boden, was Atmosphärische Gegenstrahlung genannt wird. In diesem Modell erwärmen die Treibhausgase die Planetenoberfläche auf eine höhere Temperatur, als ohne sie beobachtbar wäre. Dieser Temperaturversatz führt zu einer verstärkten Abstrahlung, bis letztlich auch der zunächst zurückgehaltene Teil der eingestrahlten Wärme an der Oberseite der Atmosphäre abgestrahlt wird.[2]

Der Modellplanet

Für den Modellplaneten werden folgende vereinfachte Annahmen getroffen und Größen betrachtet:

Der Planet hat perfekte Kugelgestalt.
Der Planet erhält eine zeitlich konstante Strahlung (das Sonnenlicht) von seinem Zentralgestirn.
S₀ bezeichnet die Solarkonstante des Planeten. Diese gibt für exakt senkrecht auf der Planetenoberfläche auftreffendes Sonnenlicht die Bestrahlungsstärke an.
Der Planet hat eine von Ort und Zeit unabhängige Albedo, die auch als von der Wellenlänge des einfallenden Sonnenlichts unabhängig angenommen wird.
α_P bezeichnet die Albedo des Planeten.
T_s bezeichnet die Temperatur der Planetenoberfläche – diese wird als überall konstant angenommen. Der Index s steht für englisch surface.
T_a bezeichnet die Temperatur der Atmosphäre des Planeten – auch diese wird als überall konstant angenommen.
Der Planet ist bezüglich Strahlung und Temperatur im Gleichgewicht: Abhängig von der erhaltenen Strahlungsmenge haben sich die beiden Temperaturen T_s und T_a passend eingestellt.

Im Gleichgewicht stellen sich Werte für T_s und T_a ein, so dass die von der Oberseite der Atmosphäre abgegebene Strahlungsleistung gleich der von der Atmosphäre absorbierten Strahlungsleistung ist. Das ankommende Sonnenlicht ist kurzwellig und die vom Planeten abgegebene Strahlung langwellig. Beide Strahlungsströme haben eigene, unterschiedliche Emissions- und Absorptionscharakteristiken.

Im idealisierten Modell nehmen wir zusätzlich an, dass die Atmosphäre für Sonnenlicht vollständig transparent ist und die Oberfläche für langwellige Strahlung einen Emissionsgrad von 1 besitzt, also ein Schwarzkörper ist. Wie oben schon erwähnt, ist nach dem Kirchhoffschen Strahlungsgesetz der Absorptionsgrad der Atmosphäre bei jeder Wellenlänge gleich ihrem Emissionsgrad. Die von der Oberfläche des Planeten abgegebene Strahlung kann im Vergleich zur Atmosphäre eine leicht verschiedene spektrale Zusammensetzung zeigen. Im Modell wird angenommen, dass der mittlere Emissionsgrad (= Absorptionsgrad) beider Strahlströme bei der Interaktion mit der Atmosphäre identisch ist. Folglich steht das Symbol ε für Emissions- und Absorptionsgrad jedes Infrarotstrahlungsstroms der Atmosphäre.

Modellrechnung

Der Planet mit seiner Oberfläche wurde als Schwarzkörper angenommen; die Oberfläche emittiert entsprechend dem Stefan-Boltzmann-Gesetz pro Quadratmeter einen Strahlungsfluss von

F=\sigma \,T_{s}^{4}

,

wobei σ die Stefan-Boltzmann-Konstante mit einem Wert von $\sigma \approx 5{,}670\,374\cdot 10^{-8}\,{\frac {\mathrm {W} }{\mathrm {m^{2}K^{4}} }}$ ist; es handelt sich um eine abgeleitete Naturkonstante.[3]

Für die gesamte Oberflächenemission muss obige Formel noch mit der Planetenoberfläche multipliziert werden. Zugunsten einfacherer Formeldarstellungen verzichten wir im Folgenden hierauf und stellen auf die Emission je Quadratmeter der Oberfläche („Strahlungsdichte“) ab.

Für die Strahlungsdichte der von der Atmosphäre ins Weltall abgegebenen Infrarotstrahlung stellen wir folgende Bilanzgleichung – textlich sowie als Formel – auf:

(1)	Gesamtabstrahlung der Atmosphäre nach oben = Abstrahlung der Atmosphäre nach oben + nicht von der Atmosphäre absorbierter Teil der Abstrahlung der Erdoberfläche
	$F_{\uparrow }=\varepsilon \sigma T_{a}^{4}+(1-\varepsilon )\sigma T_{s}^{4}$

Im zweiten Summanden ist ε der Anteil der von der Oberfläche abgehenden Strahlung, der absorbiert wird, also der Absorptionsgrad der Atmosphäre. Im ersten Summanden ist ε der Emissionsgrad der Atmosphäre, die Anpassung des Stefan-Boltzmann-Gesetzes, um dem Umstand gerecht zu werden, dass die Atmosphäre nicht optisch dicht ist. Hier wirkt sich eine weitere Vereinfachung im idealisierten Modell aus: Wir nehmen implizit an, dass die Atmospähre eine infinitesimal dünne Schicht um die Planetenoberfläche ist, so dass die abstrahlende Oberfläche der Atmosphäre exakt gleich der Planetenoberfläche selbst ist.

Damit der Netto-Strahlungsfluss an der Oberseite der Atmosphäre verschwindet, muss folgende Gleichheit gegeben sein:

(2)	Einstrahlung von der Sonne = Abstrahlung der Atmosphäre nach oben + nicht von der Atmosphäre absorbierter Teil der Abstrahlung der Planetenoberfläche
	${\frac {S_{0}}{4}}(1-\alpha _{p})=\varepsilon \sigma T_{a}^{4}+(1-\varepsilon )\sigma T_{s}^{4}$

Die Flussdichte einfallender Solarstrahlung wird durch die Solarkonstante S₀ spezifiziert. Da die Oberfläche des idealisierten Planeten als Kugel das Vierfache ihres Querschnitts (auch: Schattens) ist, ist die oberflächenbezogen einfallende Strahlung S₀/4. Die planetare Albedo α_P ist der Teil einfallender Solarstrahlung, der zurück ins All reflektiert wird. Dabei ist es gleichgültig, zu welchen Teilen die Reflexion an der Planetenoberfläche oder an der Oberseite der Atmosphäre zustande kommt.

Damit der Netto-Strahlungsfluss an der Planetenoberfläche verschwindet, muss gegeben sein:

(3)	Abstrahlung der Planetenoberfläche = Einstrahlung von der Sonne + Abstrahlung der Atmosphäre nach unten
	$\sigma T_{s}^{4}={\frac {S_{0}}{4}}(1-\alpha _{p})+\varepsilon \sigma T_{a}^{4}$

Ein Energiegleichgewicht der Atmosphäre kann durch Einsetzen von (2) in (3) abgeleitet werden:

(4)	Abstrahlung der Planetenoberfläche = Gesamte Abstrahlung der Atmosphäre
	$\varepsilon \sigma T_{s}^{4}=2\varepsilon \sigma T_{a}^{4}$

Man beachte den wichtigen Faktor 2, der sich daraus ergibt, dass die Atmosphäre sowohl nach oben wie auch nach unten abstrahlt.

Diese Gleichung kann nach T_a aufgelöst werden:

(5) $T_{a}={\frac {T_{s}}{2^{1/4}}}\approx {\frac {T_{s}}{1{,}189}}$

Für unser idealisiertes Modell ist das Verhältnis der beiden Temperaturen also völlig unabhängig von ε, dem Absorptionsgrad der Atmosphäre.

Mit (5) eingesetzt in (2) erhält man eine Lösung für T_s als Funktion der Eingangsparameter:

{\frac {S_{0}}{4}}(1-\alpha _{p})=\left(1-{\frac {\varepsilon }{2}}\right)\sigma T_{s}^{4}

oder umgestellt:

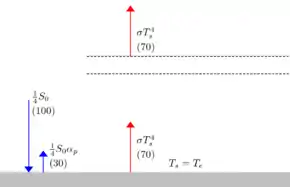
(6) $T_{s}=\left({\frac {S_{0}(1-\alpha _{p})}{4\sigma \left({1-{\frac {\varepsilon }{2}}}\right)}}\right)^{1/4}$

Für das Gesamtsystem aus dem Planeten (den wir oben als Schwarzkörper angenommen haben) und seiner Atmosphäre, dessen Gesamtabstrahlung wir oben mit $F_{\uparrow }$ bezeichnet haben, kann auch eine effektive Temperatur T_e angegeben werden. Es ist dies die Temperatur, die die Strahldichte $F_{\uparrow }$ charakterisiert, unter der Annahme, dass der Planet inklusive seiner Atmosphäre als Gesamtsystem ein perfekter Strahler mit $F_{\uparrow }=\sigma T_{e}^{4}$ wäre. Im idealisierten Modell ist dies einfach darstellbar: T_e ist ebenso die Lösung für T_s für den Fall von ε = 0, also einer fehlenden Atmosphäre. In diesem Fall vereinfacht sich (6) zu (7):

(7) $T_{e}=\left({\frac {S_{0}(1-\alpha _{p})}{4\sigma }}\right)^{1/4}$

Die so ermittelte effektive Temperatur T_e ergibt in (6) eingesetzt:

(8) $T_{s}={\frac {1}{\left(1-{\frac {\varepsilon }{2}}\right)^{1/4}}}\,T_{e}$

Anwendung auf den Planeten Erde

Idealisiertes Treibhausmodell mit isothermer Atmosphäre. Der blaue Pfeil markiert kurzwelligen solaren Strahlungsfluss, der rote Pfeil stellt den langwelligen, vom Planeten emittierten Strahlungsfluss dar. Die Strahlströme werden für eine bessere Visualisierung in der Grafik seitlich versetzt dargestellt; im Modell findet beides am selben Ort statt. Die Atmosphäre wird als Schicht zwischen den gestrichelten Linien dargestellt; sie wechselwirkt nur mit langwelliger Infrarotstrahlung. Eine spezielle Lösung wurde für die Werte ε=0,78 und α_p=0,3 angegeben. Sie repräsentiert den Planeten Erde. Die Zahlen in Klammern sind die Flussdichten in Prozent von S₀/4.

Die Gleichgewichtslösung mit ε=0,82. Eine Erhöhung um Δε=0,04 entspricht einer Verdopplung der Kohlenstoffdioxidkonzentration und der damit einhergehenden Wasserdampfrückkopplung

Die Gleichgewichtslösung ohne Treibhauseffekt: ε=0

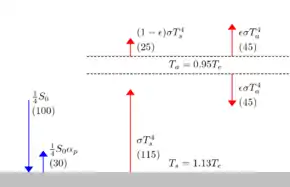
Beim Planeten Erde beträgt die Solarkonstante $S_{0}=1366\;\mathrm {W} /\mathrm {m} ^{2}$ und die Albedo im Mittel rund $\alpha _{p}=0{,}3$ .

Modellergebnisse

Bei einem perfekten Treibhaus, bei dem keine Strahlung von der Oberfläche entweichen kann, also ε = 1 gilt mit (6):

{\begin{aligned}T_{s}&=303~\mathrm {K} =30~{}^{\circ }\mathrm {C} \\T_{a}&=254~\mathrm {K} =-19~{}^{\circ }\mathrm {C} \end{aligned}}

Für die globale durchschnittliche Oberflächentemperatur T_s kennt man einen Schätzwert von ungefähr 288 K, also etwa 15 °C.[4] Um diesen einzustellen, variiert man den Parameter ε. Für ε = 0,78, was bedeutet, dass 22 Prozent der von der Oberfläche emittierten Strahlung direkt ins All entweichen, gilt mit (6):

{\begin{aligned}T_{s}&=288{,}3~\mathrm {K} =15{,}1~^{\circ }\mathrm {C} \\T_{a}&=242{,}5~\mathrm {K} =-30{,}7~^{\circ }\mathrm {C} \end{aligned}}

.

Die zugehörige effektive Temperatur ergibt sich mit der Gleichung (8) als

T_{e}=255~\mathrm {K} =-18~{}^{\circ }\mathrm {C}

Temperaturänderung durch Strahlungsantrieb

Der aus einer Verdopplung der atmosphärischen Kohlenstoffdioxidkonzentration resultierende Strahlungsantrieb beträgt bei einfacher Parametrierung 3,71 W/m² Dies ist auch der vom IPCC angegebene Wert.

Aus der Gleichung für $F_{\uparrow }$ (1) folgt:

\Delta F_{\uparrow }=\Delta \varepsilon \left(\sigma T_{a}^{4}-\sigma T_{s}^{4}\right)

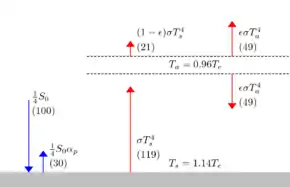
Mit den Werten von T_s und T_a für ε = 0,78 ergibt sich für $\Delta F_{\uparrow }=-3{,}71\;\mathrm {W} /\mathrm {m} ^{2}$ mit Δε = 0,019. Folglich ist eine Veränderung von ε von 0,78 auf 0,80 in Übereinstimmung mit dem Strahlungsantrieb, der aus der Verdoppelung der Kohlenstoffdioxidkonzentration erwächst. Für ε = 0,80 beträgt:

T_{s}=289{,}5~\mathrm {K}

Folglich sagt dieses Modell eine globale Erwärmung um ΔT_s = 1,2 K für eine Verdopplung der Kohlenstoffdioxidkonzentration voraus. Eine Vorhersage eines typischen Klimamodells ergibt eine Erwärmung der Erdoberfläche um 3 K. Dies liegt primär daran, dass Klimamodelle die positive Rückkopplung berücksichtigen, die in erster Linie aus der Wasserdampf-Rückkopplung resultiert. Mit einem einfachen Trick kann dieser Effekt berücksichtigt werden. Hierzu wird Δε um 0,02 auf insgesamt Δε = 0,04 erhöht. Damit wird dem Effekt einer durch die Erwärmung ausgelösten erhöhten Wasserdampfkonzentration näherungsweise Rechnung getragen. Dieses idealisierte Modell sagt für eine verdoppelte Kohlenstoffdioxidkonzentration dann eine globale Erwärmung um ΔT_s = 2,4 K voraus, was mit den Angaben des IPCC in etwa übereinstimmt.

Bewertung der Modellannahmen für die Erde

Die Annahme der perfekten Kugelgestalt gilt als eine gute Näherung für die Erde.

Die Annahme der konstanten Sonnenstrahlung in Kombination mit der planetenweiten Konstanz einer einheitlichen Oberflächen- und Atmosphärentemperatur T_a und T_s ist dagegen weit entfernt von den realen Verhältnissen auf der Erde. Als Rechtfertigung des idealisierten Modells wird angeführt, dass sich auf der Erde Temperaturunterschiede durch Konvektion angleichen. An der Erdoberfläche geschieht dies beispielsweise durch das Vorhandensein von Meeresströmungen, die zu einer starken Durchmischung führen.

Dennoch sind die Verhältnisse auf der Erde wesentlich abweichend vom Idealbild:

Die sogenannte Solarkonstante schwankt, insbesondere in Folge des Sonnenfleckenzyklus.
Die Sonnenstrahlung auf jedem Punkt der Erde variiert gemäß der Drehung der Erde um die Sonne und ihrer Präzession im Tages- und im Jahresablauf stark.
Eine Durchmischung der Temperaturen findet nur sehr unvollkommen statt:
- Ganzjährig ist es beispielsweise auf der Erdoberfläche in der Äquatorialzone wesentlich wärmer als in den Polarzonen.
- Die Biosphäre, insbesondere die Pflanzenwelt, trägt erheblich zu zeitlichen Schwankungen bei; beispielsweise beeinflusst das Pflanzenwachstum die Albedo sowie den CO₂-Gehalt der Atmosphäre und die Verdunstungsleistung der Vegetation beeinflusst den Wasserkreislauf in der Atmosphäre.
- Bei Sonneneinstrahlung erwärmt sich beispielsweise Sandboden stark, die Meeresoberfläche dagegen nur sehr wenig.
- In der Atmosphäre wechseln sich warme und kalte Schichten ab, deren Temperatur sich durch Effekte wie das Wetter nur sehr eingeschränkt durchmischt.

Varianten und Erweiterungen

Alternativ kann im dargestellten idealisierten Treibhausmodell statt der Oberflächen- und der Atmosphärentemperatur auch ein Paar aus der Atmosphärentemperatur einer unteren und einer oberen Atmosphärentemperatur betrachtet werden.

Das dargestellte einschichtige Atmosphärenmodell kann unmittelbar in ein mehrschichtiges Atmosphärenmodell umgewandelt werden. Hierfür müssen die Gleichungen für die Temperaturen in eine Reihe gekoppelter Gleichungen für die einzelnen Schichten umgeformt werden. Dieses einfache Modell sagt immer eine mit zunehmender Höhe abnehmende Temperatur voraus und die Temperatur aller Schichten nimmt mit steigender Treibhausgaskonzentration zu. Keine dieser Annahmen ist für die Erde realistisch: In der Erdatmosphäre steigen die Temperaturen oberhalb der Tropopause an und bei Erhöhung der Treibhausgaskonzentration wird erwartet,[5] und beobachtet,[6] dass die Temperaturen dort (in der Stratosphäre) sinken. Der Grund ist, dass die Erdatmosphäre nicht für alle optischen Wellenlängenbereiche dieselbe Transmissivität besitzt.

Literatur

Craig F. Bohren, Eugene E. Clothiaux: Fundamentals of Atmospheric Radiation. John Wiley & Sons, Chichester 2006, ISBN 3-527-40503-8, 1.6 Emissivity and Global Warming, S. 31–41 (englisch).
Grant W. Petty: A First Course in Atmospheric Radiation. 2. Auflage. Sundog Pub, Madison, Wisconsin 2006, ISBN 0-9729033-1-3, 6.4.3 Simple Radiative Models of the Atmosphere, S. 139–143 (englisch).
Prof. Dr. Dr. h. c. Gerhard G. Paulus, Physikalisch-Astronomische Fakultät Friedrich-Schiller-Universität Erderwärmung zum Nachrechnen

Einzelnachweise

Chapter 2, The global energy balance (PDF; 654 kB), UT course Physical Climatology
What is the Greenhouse Effect? (PDF; 1,9 MB) Intergovernmental Panel on Climate Change. 2007. Abgerufen am 12. März 2013.
Stefan-Boltzmann constant. National Institute of Standards and Technology, abgerufen am 20. Juli 2019 (englisch).
R. Gieré, Peter Stille: Energy, Waste and the Environment: A Geochemical Perspective. Geological Society of London, 2004, ISBN 1-86239-167-X, S. 162 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
J. Hansen, D. Johnson, A. Lacis, S. Lebedeff, P. Lee, D. Rind, G. Russell: Climate Impact of Increasing Atmospheric Carbon Dioxide. In: Science. Band 213, Nr. 4511, 28. August 1981, S. 957, doi:10.1126/science.213.4511.957 (atmos.washington.edu archiviert bei web.archive.org [PDF; abgerufen am 23. Juni 2019]).
B. D. Santer, J. F. Painter, C. Bonfils, C. A. Mears, S. Solomon, T. M. L. Wigley, P. J. Gleckler, G. A. Schmidt, C. Doutriaux, N. P. Gillett, K. E. Taylor, P. W. Thorne, F. J. Wentz: Human and natural influences on the changing thermal structure of the atmosphere. In: Proceedings of the National Academy of Sciences. Band 110, Nr. 43, 22. Oktober 2013, S. 17235, doi:10.1073/pnas.1305332110.

Weblinks

R. Tuckermann: Skript Atmosphärenchemie (PDF; 1,8 MB)
Vorlesungen von David Archer: Our First Climate Model und The Greenhouse Effect (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Chapter 2, The global energy balance (PDF; 654 kB), UT course Physical Climatology

[2] What is the Greenhouse Effect? (PDF; 1,9 MB) Intergovernmental Panel on Climate Change. 2007. Abgerufen am 12. März 2013.

[3] Stefan-Boltzmann constant. National Institute of Standards and Technology, abgerufen am 20. Juli 2019 (englisch).

[4] R. Gieré, Peter Stille: Energy, Waste and the Environment: A Geochemical Perspective. Geological Society of London, 2004, ISBN 1-86239-167-X, S. 162 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).

[Hansen-5] J. Hansen, D. Johnson, A. Lacis, S. Lebedeff, P. Lee, D. Rind, G. Russell: Climate Impact of Increasing Atmospheric Carbon Dioxide. In: Science. Band 213, Nr. 4511, 28. August 1981, S. 957, doi:10.1126/science.213.4511.957 (atmos.washington.edu archiviert bei web.archive.org [PDF; abgerufen am 23. Juni 2019]).

[DOI10.1073/pnas.1305332110-6] B. D. Santer, J. F. Painter, C. Bonfils, C. A. Mears, S. Solomon, T. M. L. Wigley, P. J. Gleckler, G. A. Schmidt, C. Doutriaux, N. P. Gillett, K. E. Taylor, P. W. Thorne, F. J. Wentz: Human and natural influences on the changing thermal structure of the atmosphere. In: Proceedings of the National Academy of Sciences. Band 110, Nr. 43, 22. Oktober 2013, S. 17235, doi:10.1073/pnas.1305332110.