Transitmethode

Die Transitmethode ist ein photometrisches Verfahren zum Nachweis von Exoplaneten. Bis 2019 wurden mit dieser Methode etwa 80 % aller bisher bekannten Planeten entdeckt,[1] was sie zur erfolgreichsten Methode auf der Suche nach Exoplaneten macht. Der Planet wird dabei nicht direkt beobachtet, sondern nur indirekt durch Beobachtung des Helligkeitsverlaufs seines Sterns nachgewiesen. Ein Großteil der bisherigen Entdeckungen ist mithilfe des Kepler Weltraumteleskops gelungen.

Fortdauernde Messungen lassen im Falle eines Transitplaneten geringe, periodische Helligkeitseinbrüche erkennen.

Ein Planetentransit verursacht einen Helligkeitsabfall des beobachteten Sterns.

Zusammenfassung

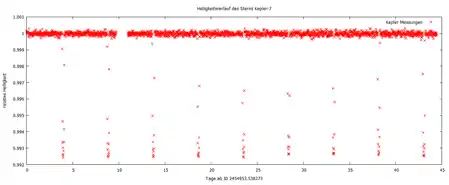
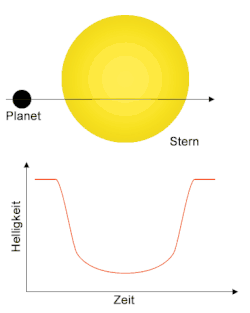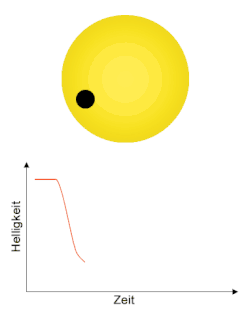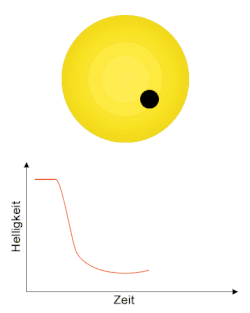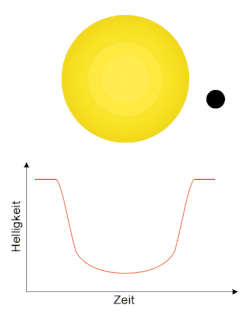
Während eines Planetentransits verdeckt der Planet für einen geeignet gelegenen Beobachter einen Teil seines Muttersterns, sodass die Helligkeit des Sterns während des Transits reduziert ist. Durch fortwährende Beobachtung der Helligkeit eines Sterns lassen sich diese Veränderungen nachweisen. Der Planet, welcher einen Transit hervorruft, wird Transitplanet (englisch transiting planet) genannt. Planeten umkreisen ihren Stern auf ihrer Bahn innerhalb einer bestimmten Umlaufdauer, sodass nach einem Umlauf erneut ein Transit stattfindet. Um ein zufälliges Ereignis auszuschließen, müssen mindestens drei Transits mit gleichem zeitlichen Abstand zueinander beobachtet werden. Obwohl die Wahrscheinlichkeit einen Transit bei einem zufällig ausgewählten Stern zu beobachten mit weniger als 1 %[2] recht gering ist, weil die Umlaufbahnen auch so orientiert sein können, dass der Planet von der Erde aus gesehen nie vor seinem Stern vorbeizieht, wurden bis August 2019 mit dieser Methode über 3000[1] Exoplaneten nachgewiesen. Aus der Beobachtung der Helligkeitsverläufe der Sterne lassen sich weitere Informationen über den Planeten und den Stern gewinnen. So sind beispielsweise Aussagen über die Umlaufdauer um seinen Stern, den Planetenradius, die Bahnneigung seiner Umlaufbahn gegenüber der Sichtlinie und über die Rotationsrichtung seines Sterns möglich. Darüber hinaus lassen sich aus der Kenntnis dieser Werte Aussagen über den Abstand treffen, in dem der Planet seinen Stern umkreist. Bei spektroskopischer Beobachtung lassen sich auch Daten über die Zusammensetzung seiner Atmosphäre und über seine Albedo und Temperatur gewinnen. Die Genauigkeit der Methoden reichte zwar Anfang 2017 noch nicht aus, um auch Informationen über erdähnliche Planeten zu gewinnen, jedoch werden in naher Zukunft Messungen für erdähnliche Planeten mit Fertigstellung lichtstarker Teleskope wie dem James-Webb-Weltraumteleskop möglich.^[veraltet][3][4][5]

Abschätzung zur Wahrscheinlichkeit eines Transits

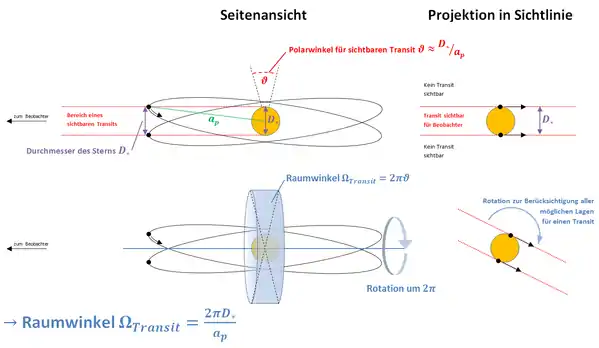
Überlegung zur Berechnung der Beobachtungswahrscheinlichkeit mithilfe des Raumwinkels, für den ein Transit beobachtbar ist. Der Beobachter ist als sehr weit entfernt angenommen.

Darstellung der Transitwahrscheinlichkeit in Abhängigkeit vom Stern- und Planetenbahnradius

Unter der Annahme, dass die Umlaufbahnen der Planeten zufällig im Raum orientiert sind, lässt sich die Wahrscheinlichkeit, dass ein weit entfernter Beobachter einen Transit beobachten kann, mithilfe geometrischer Überlegungen berechnen. Ein Transit ist nur dann beobachtbar, wenn der Planet vom Beobachter aus gesehen vor seinem Stern vorbeizieht und damit den Stern teilweise verdeckt. Unter der Annahme, dass der Radius des Planeten $R_{p}$ im Vergleich zum Sternradius $R_{*}$ zu vernachlässigen ist, da zumeist $R_{p}\ll R_{*}$ , lässt sich der Winkelbereich der Bahnneigung, in der ein Transit stattfinden kann, abschätzen zu $\vartheta \approx D_{*}/a_{p}=2R_{*}/a_{p}$ , wobei unter Annahme einer Kreisbahn mit $a_{p}$ der Abstand des Planeten zum Stern gegeben ist. Da jedoch auch im Fall eines beobachtbaren Transits die Bahnebene in der Sichtlinie beliebig orientiert liegen kann, lässt sich für den dreidimensionalen Anteil der Orientierung, in dem ein Transit stattfindet, der Raumwinkel angeben als $\Omega _{\text{Transit}}=2\pi D_{*}/a_{p}$ . Ist davon auszugehen, dass die Umlaufbahnen der Exoplaneten zufällig im Raum orientiert sind, lässt sich die Wahrscheinlichkeit $p$ , einen Transit beobachten zu können, als Verhältnis zum gesamten Raumwinkel $4\pi$ angeben. Damit ergibt sich

p={\frac {\Omega _{\text{Transit}}}{\Omega _{\text{gesamt}}}}={\frac {R_{*}}{a_{p}}}

.

Der Sternradius $R_{*}$ lässt sich über das Spektrum, dessen Helligkeit und gut verstandene theoretische Sternenmodelle gewinnen (siehe auch Hertzsprung-Russell-Diagramm). Die Wahrscheinlichkeit ist für einen gegebenen Sternradius umgekehrt proportional zur großen Halbachse der Planetenbahn. Mithilfe des 3. Keplerschen Gesetzes und bekannter Sternenmasse $M_{*}$ , die ebenfalls aus den Sternenmodellen bekannt ist, lässt sich die Wahrscheinlichkeit umschreiben zu

p={\frac {R_{*}}{T^{2/3}}}\cdot \left({\frac {4\pi ^{2}}{GM_{*}}}\right)^{1/3}

,

wobei angenommen wurde, dass $M_{p}\ll M_{*}$ ist, und $T$ die Umlaufdauer des Planeten beschreibt. Zu erwarten ist demnach, dass Planeten mit einer niedrigeren Umlaufdauer mit einer höheren Wahrscheinlichkeit beobachtet werden können als solche mit einer hohen Umlaufdauer, was sich auch tatsächlich in den Daten[6] zeigt.[5][7]

Beispielrechnung für unser Sonnensystem

Für Planetensysteme mit einer ähnlichen Konfiguration wie unser Sonnensystem (Sternradius ist der Sonnenradius, gleiche Anordnung der Planeten), würden sich demnach für die Wahrscheinlichkeit zur Beobachtung eines Transits folgende Werte ergeben:

Planet	große Halbachse / AE	Wahrscheinlichkeit
Merkur	00,387	1,203 %
Venus	00,723	0,644 %
Erde	01,000	0,465 %
Mars	01,520	0,306 %
Jupiter	05,200	0,090 %
Saturn	09,580	0,049 %
Uranus	19,200	0,024 %
Neptun	30,000	0,016 %

Für einen Planeten in der habitablen Zone um einen sonnenähnlichen Stern ergibt sich damit eine Beobachtungswahrscheinlichkeit von etwa 0,5 %.

Transittiefe

Helligkeitsmessungen des Weltraumteleskops Kepler am Stern Kepler-7; Zoom auf einen einzelnen Transit. Eingezeichnet ist mit

\Delta F

die Transittiefe, welche in diesem Beispiel für den Planeten Kepler-7b etwa 0,7 % beträgt.

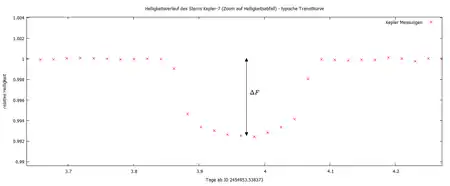
Bedeckt der Transitplanet seinen Stern, nimmt die Helligkeit ab. Der relative Abfall der Helligkeit während eines Transits gegenüber der nicht reduzierten Helligkeit des Sterns wird als Transittiefe $\Delta F$ (engl. transit depth) bezeichnet. Unter der Annahme, der Stern strahle Licht wie ein schwarzer Körper ab (was in erster Näherung eine gute Übereinstimmung liefert), lässt sich mithilfe des Stefan-Boltzmann-Gesetzes über die abgestrahlte Leistung $P=\sigma AT^{4}$ ein Ausdruck für die Transittiefe angeben. Für die Fläche des bedeckten Bereiches gilt $A_{p}=\pi R_{p}^{2}$ , für die Gesamtfläche der Sternenscheibe $A_{*}=\pi R_{*}^{2}$ . Das Stefan-Boltzmann-Gesetz kann für diese Projektionsflächen verwendet werden, obwohl die Oberfläche des Sterns der einer Kugel entspricht, da die Flächennormale $d{\vec {A}}$ für die Projektion mit $\cos(\phi )$ skaliert, wobei $\phi$ der Winkel zwischen der Sichtlinie und Radialvektor im Stern zum Flächenstück ist. Der Verlauf der Helligkeitskurve während eines Transits ist unabhängig von der Entfernung zum beobachteten Planetensystem, womit sich direkt ohne Berücksichtigung der Entfernung aus dem Verhältnis der abgestrahlten Leistungen während eines Transits $P_{tr}$ und ohne Transit $P_{0}$ ergibt:

{\frac {P_{tr}}{P_{0}}}={\frac {\sigma \left(A_{*}-A_{p}\right)T_{*}^{4}}{\sigma A_{*}T_{*}^{4}}}=1-{\frac {A_{p}}{A_{*}}}

Die Transittiefe lässt sich also als Verhältnis der beiden Radien angeben zu

\Delta F={\frac {A_{p}}{A_{*}}}={\frac {R_{p}^{2}}{R_{*}^{2}}}

.[5]

Der relative Helligkeitsabfall ist demnach in erster Näherung direkt proportional zur verdeckten Fläche $A_{p}$ und umgekehrt proportional zur Gesamtfläche $A_{*}$ der geometrisch sichtbaren Sternenscheibe.

Für unser Planetensystem ergäbe das folgende Werte für die Transittiefe.

Planet	Radius / km	Transittiefe
Merkur	02.439	0,0012 %
Venus	06.052	0,0076 %
Erde	06.378	0,0084 %
Mars	03.386	0,0024 %
Jupiter	69.170	1,0100 %
Saturn	57.310	0,7500 %
Uranus	25.270	0,1350 %
Neptun	24.550	0,1270 %

Störende Einflüsse

Die Randverdunkelung am Beispiel der Sonne, hier während eines Merkurtransits. Die Randbereiche wirken etwas dunkler als der zentrale Bereich des Sterns. Gut sichtbar ein Sonnenfleck (links), welcher sogar größer ist als Merkur.

Der Verlauf der Helligkeitskurve ist nur in erster Näherung ein einfacher Abfall der Helligkeit um $\Delta F$ . Wegen der Randverdunkelung erscheinen die Randbereiche einer Sternenscheibe dunkler als das Zentrum. Außerdem besitzt das Zentrum der Sternenscheibe einen größeren Anteil im blauen Spektrum als die Bereiche nahe dem Rand. Dies kommt von der optischen Dichte der Sternenatmosphäre, sodass wir am Rande Gebiete mit einer tieferen effektiven Temperatur sehen als im Zentrum. Da die abgestrahlte Leistung proportional zur vierten Potenz der Temperatur ist, sind kleine Änderungen der Temperatur bereits für große Veränderungen in der abgestrahlten Leistung verantwortlich, weswegen der Rand dunkler erscheint. Tritt nun ein Planet in die Sternenscheibe ein, verdeckt er zunächst einen Bereich, der dunkler als das aus der Gesamthelligkeit resultierende Mittel ist. Läuft der Planet danach weiter bis in das Zentrum der Sternenscheibe, verdeckt er einen Bereich der heller als das Mittel ist. Die Transittiefe fällt demnach zu Beginn und gegen Ende eines Transits geringer aus als während der zentralen Phase, da zu Beginn und gegen Ende Bereiche mit geringerer Strahlungsleistung und in der zentralen Phase der Bereich mit der größten Strahlungsleistung bedeckt wird. Typische Transitkurven sind deshalb während ihrer Talphase leicht konvex geformt und bestätigen somit ebenfalls ein Auftreten der Randverdunkelung bei anderen Sternen.[5]

Da Sterne, genau wie die Sonne, variable Inhomogenitäten in ihrem Magnetfeld aufweisen, bilden sich Sternenflecken (engl. star spots) aus (siehe Sonnenflecken). Diese können eine enorme Größe erreichen und erscheinen dunkler, weshalb sie einen Helligkeitsabfall verursachen, welcher in der Größenordnung eines Transits liegen kann. Damit ein Sternenfleck, der auf Grund der Rotation des Sterns ebenfalls über die Sternenscheibe wandert, nicht fälschlich als Transit gedeutet wird, muss der Helligkeitsabfall mehrmals, periodisch und stets mit der gleichen Transittiefe nachgewiesen werden. Ein weiterer Hinweis auf einen Sternenfleck ist die meist sehr viel langsamere Rotation des Sterns, sodass der Helligkeitsabfall eines Flecks mehrere Tage andauern kann, während ein Transit sich im Bereich von Stunden abspielt.[8]

Bedeckungsveränderliche Doppelsterne, die sich so umkreisen, dass sie keine komplette, aber eine streifende gegenseitige Bedeckung hervorrufen, verursachen Helligkeitseinbrüche mit einer ähnlichen Transittiefe wie die eines Planeten. Damit Beobachtungen dieser Verdunkelungen nicht als falschpositive Funde gewertet werden, ist es notwendig, den Verlauf der Helligkeitskurve genau zu vermessen. Sterne mit einer streifenden Bedeckung erzeugen einen V-förmigen Verlauf, wohingegen Planeten eine ausgedehnte Talphase verursachen. Außerdem kann bei Doppelsternen, deren effektive Oberflächentemperatur verschieden ist, eine Verschiebung des Intensitätsmaximums des Emissionsspektrums während der Bedeckung gemessen werden und so ein Planet sicher ausgeschlossen werden.[9]

Ableitbare Parameter

Mithilfe dieser Methode lassen sich einige Informationen sowohl über den Transitplaneten als auch über seinen Mutterstern gewinnen. Dabei ist es wichtig, den Helligkeitsverlauf so genau wie möglich zu bestimmen. Für die meisten Beobachtungen an Transitplaneten in der Größenordnung von Hot Jupiters reichen Beobachtungen von der Erdoberfläche aus. Um den Helligkeitsverlauf jedoch auch für erdähnliche Planeten vermessen zu können, ist es nötig, die Messungen vom Weltall aus durchzuführen, um atmosphärischen Störungen zu entfliehen. Dies ist die Hauptaufgabe von Weltraumteleskopen wie Kepler.

Umlaufperiode und große Halbachse des Planeten

Ohne explizite große Störungen bleibt die Bahn eines Planeten auf Grund der Drehimpulserhaltung, genau wie in unserem Sonnensystem, stabil. Wird also ein Transit beobachtet, findet nach einem Umlauf erneut ein Transit statt. Der zeitliche Abstand zwischen zwei Transits des gleichen Planeten bleibt dabei konstant und entspricht genau der Umlaufdauer des Planeten um seinen Stern. Mithilfe des 3. Keplerschen Gesetzes und der Kenntnis der Sternenmasse (welche mithilfe von Sternenmodellen allein aus dem Spektrum und der Leuchtkraft des Sterns ermittelt werden kann) lässt sich die große Halbachse des Planeten berechnen.[4][5][7]

Um auszuschließen, dass zufällig ein anderes Objekt (wie beispielsweise ein Planemo) zwischen dem Beobachter und dem beobachteten Stern vorbeizieht und einen Helligkeitsabfall verursacht, müssen mindestens drei Transits beobachtet werden, welche im selben zeitlichen Abstand zueinander stattfanden. Um einen Transitplaneten nachzuweisen, muss sein Stern also für mindestens die doppelte Zeit beobachtet werden, welche der Planet benötigt, um seinen Mutterstern zu umkreisen.[10]

Bahnneigung

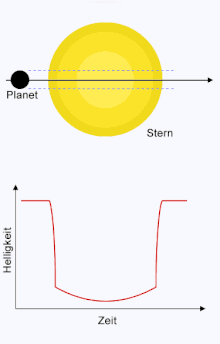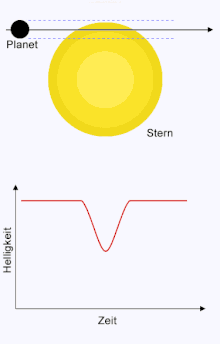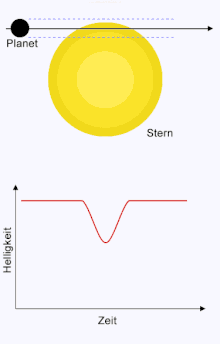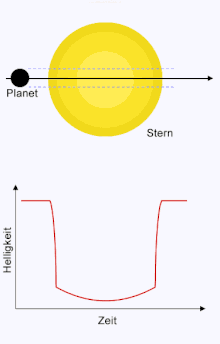
Veranschaulichung des Helligkeitsverlaufs eines Planetentransits mit verschiedenen Zentralitäten. Die gestrichelte Linie kennzeichnet den Bereich, der vom Planeten bedeckt wird.

Wird der Helligkeitsverlauf genau vermessen, kann die Bahnneigung gegenüber der Sichtlinie mithilfe der analytischen Näherung des Helligkeitsverlaufs bestimmt werden. Der Verlauf der Kurve hängt davon ab, ob der Planet zentral, versetzt, streifend oder gar nicht über die Sternenscheibe wandert. Zusammen mit der Masse des Sterns und der Entfernung des Planeten von diesem, lässt sich bei Kenntnis, wie zentral der Transit verläuft, die Bahnneigung angeben. Der Abstand zum Mittelpunkt der Sternenscheibe wird Zentralparameter genannt. Durch Methoden der Ausgleichsrechnung lassen sich die bestimmenden Parameter aus den gemessenen Datenpunkten nähern. Ausschlaggebend für die Bestimmung der Bahnneigung sind insbesondere die Flanken der Transitkurve.[5]

Planetenradius und Dichte

Mithilfe der Transittiefe und des aus Sternmodellen bekannten Sternradius lässt sich der Planetenradius bestimmen. Mit dem im Abschnitt Transittiefe hergeleiteten Ausdruck lässt sich für den Planetenradius $R_{p}$ finden:

R_{p}=R_{*}{\sqrt {\Delta F}}

Für Planeten mit hinreichend großer Masse lässt sich mithilfe der Radialgeschwindigkeitsmethode, welche sonst nur die Mindestmasse eines Exoplaneten liefern kann,[11] die Masse nun wegen Kenntnis über die Bahnneigung des Planeten genauer bestimmen. Mithilfe des Radius des Planeten und seiner Masse ist eine Angabe über seine durchschnittliche Dichte möglich. Damit sind Aussagen über die Natur des Planeten möglich, ob es sich etwa um einen Gas- oder einen Gesteinsplaneten handeln muss.[5][11]

Zusammensetzung der Atmosphäre des Planeten

Befindet sich der Planet vor seinem Mutterstern, besteht die Möglichkeit spektroskopisch Informationen über die Atmosphäre des Planeten zu erhalten. Er verdeckt während eines Transits nicht nur das Licht des Sternes, sondern seine Atmosphäre wird auch vom Licht des Sterns durchschienen, ähnlich wie beim Lomonossow-Effekt. Wie bei jedem Gas, das von einem kontinuierlichen Spektrum durchschienen wird, zeigen sich Absorptionslinien. Diese können im Vergleich mit spektralen Messungen des Sterns außerhalb eines Transits identifiziert werden. Die Stärke der entstehenden Absorptionslinien bewegt sich in der Größenordnung von 0,001 bis 0,01 % der im Sternspektrum nachweisbaren Fraunhoferlinien. Die geringe Ausprägung rührt daher, dass die vom Sternenlicht durchschienene Atmosphäre nur etwa 0,001 bis 0,01 % der projizierten Fläche der Sternenscheibe ausmacht und daher nur ein Bruchteil des Lichts mit der Information über die Zusammensetzung der Atmosphäre vorhanden ist. Der überwiegende Rest des Lichts ist unverändertes Licht des Sternes. Je kleiner der Planet ist, desto mehr Messungen sind nötig um das Signal-Rausch-Verhältnis zu verbessern und überhaupt ein brauchbares Datenset zu generieren. Mit den Anfang 2016 zur Verfügung stehenden Instrumenten war es noch nicht möglich, für erdähnliche Planeten Aussagen über deren Atmosphäre zu treffen. Mit der Fertigstellung sehr lichtstarker Teleskope wie des European Extremely Large Telescopes oder des James-Webb-Weltraumteleskops ^[veraltet] und Anwendung neuer Spektroskopieverfahren wird dies in Zukunft möglich sein.[3][12][13]

Albedo und Temperatur des Planeten

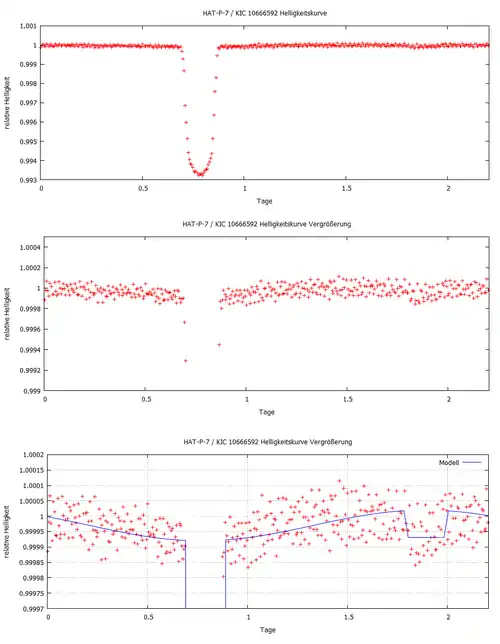
Helligkeitsverlauf des Sterns HAT-P-7 während eines Umlaufs seines Planeten HAT-P-7b. Gut zu erkennen die periodische Änderung der Helligkeitskurve, welche durch die Phase des Planeten hervorgerufen wird. Die Bedeckung des Planeten durch den Stern verursacht den zweiten, kleineren Helligkeitsabfall.

Der den Stern umkreisende Transitplanet wird bei kleiner Exzentrizität, also einer annähernden Kreisbahn, nicht nur einen Transit hervorrufen, sondern wird ebenfalls vom Stern verdeckt werden. Ähnlich wie bei einem bedeckungsveränderlichen Stern entsteht so ein zusätzlicher kleiner Helligkeitsabfall, wenn der Planet bedeckt wird. Da der Planet nicht selbst leuchtet, sondern das Licht des Sterns reflektiert, entsteht außerdem eine Modulation der Helligkeitskurve auf Grund der Phase des Planeten. Wendet er dem Beobachter seine Schattenseite zu, was direkt vor, während, oder nach einem Transit der Fall ist, erreicht diesen nur die Helligkeit des Sterns. Je weiter er auf seiner Bahn um den Stern läuft, um so mehr seiner Tagseite ist für den Beobachter sichtbar und die Helligkeit, die gemessen werden kann, nimmt zu. Je größer der Planet ist und je größer seine Albedo, desto größer ist dieser Effekt. Sobald der Planet hinter seinen Stern wandert, nimmt die Helligkeit um diesen Beitrag ab und ein Beobachter erhält nur noch den Strahlungsfluss des Sterns alleine. Diese Phase wird Bedeckung (engl. eclipse) genannt, weil das beobachtete Objekt, hier der Planet, verdeckt wird. Nach der Bedeckung steigt die Helligkeit wieder an, sobald die Tagseite des Planeten wieder sichtbar wird und nimmt im Laufe der Zeit wieder ab, bis der Planet erneut vor der Sternenscheibe einen Transit vollzieht. Für Umlaufbahnen mit einer großen Exzentrizität ist es möglich, dass der Transit in der Periapsis stattfindet und einen Transit hervorruft, eine Bedeckung in der Apoapsis jedoch nicht stattfinden kann, da die große Entfernung im sternfernen Punkt bei gegebener Bahnneigung ausreicht, um für eine Projektion bereits außerhalb der Sternenscheibe zu liegen.

Lichtkurven mit Modulation durch die Phase des Planeten und einer zusätzlichen Bedeckung sind für Planeten in der Größenordnung des Jupiters bereits nachgewiesen worden, siehe beispielsweise HAT-P-7b, und verraten zusammen mit dem ebenfalls bestimmbaren Radius etwas über sein Rückstrahlvermögen, die Albedo. Zusammen mit der Albedo und der ebenfalls berechenbaren Distanz zum Stern lassen sich damit Aussagen über seine Oberflächentemperatur machen. Gelingt es außerdem das Spektrum kurz vor oder kurz nach einer Bedeckung zu vermessen und diese spektroskopische Messung mit der während einer Bedeckung zu vergleichen, lassen sich sogar Aussagen über das Reflexionsspektrum des Planeten machen. Für erdähnliche Planeten ist eine derartige Messung für Albedo, Temperatur und Reflexionsspektrum wegen nicht ausreichender Genauigkeit noch nicht erfolgt. Mit neuen lichtstarken Teleskopen wird dies in naher Zukunft möglich sein.^[veraltet][3][14][15]

???????
Schema für das Planetensystem um den Stern HAT-P-7

Weitere Möglichkeiten

Rotationsrichtung des Sterns

Während eines Transits zieht der Planet von einer Seite in die Sternenscheibe und bedeckt zunächst einen Teil des Randgebietes. Er zieht weiter über den Zentralbereich der Sternenscheibe und wird auf der zur Eintrittsstelle gegenüberliegenden Seite wieder aus der Sternenscheibe heraustreten. Diesem Umstand ist es zu verdanken, dass wir Informationen über die Rotation des Sterns erhalten können. Die Absorptionslinien eines Sterns sind verbreitert. Aus der Breite der Spektrallinien im Licht eines Sternes lassen sich mithilfe des Dopplereffekts Rückschlüsse auf die Tangentialgeschwindigkeit und somit die Rotation des Sterns ziehen. Bedeckt der Planet den Randbereich, dessen Gas sich auf den Beobachter zu bewegt, nimmt der ins Blaue verschobene Anteil des Lichts ab. Das Mittel der Linie wandert scheinbar ins Rote. Während der Planet zentral vor dem Stern steht, verschwindet diese Verschiebung. Auf der gegenüberliegenden Seite bedeckt er Bereiche, die ins Rote verschoben sind, weil sie sich vom Beobachter wegbewegen. Das Mittel verschiebt sich ins Blaue (siehe auch Rossiter-McLaughlin-Effekt). Diese Verschiebung des Linienmittels während eines Transits ermöglicht Aussagen über die minimale Rotationsgeschwindigkeit[16] des Sterns. Außerdem lässt sich entscheiden, ob der Stern in der gleichen Richtung rotiert, wie ihn sein Planet umkreist, oder ob der Stern gegenläufig rotiert. Wird bei Eintritt eine Verschiebung ins Rote festgestellt und bei Austritt eine Verschiebung ins Blaue, rotiert der Stern in der gleichen Richtung wie sein Begleiter und andersherum.[5][16]

Untersuchung des Magnetfelds des Sterns

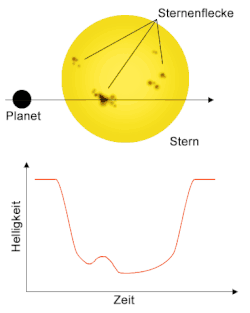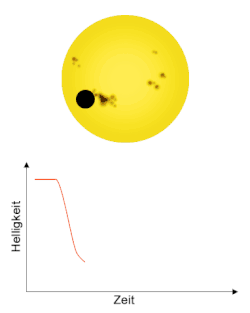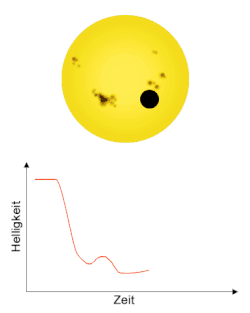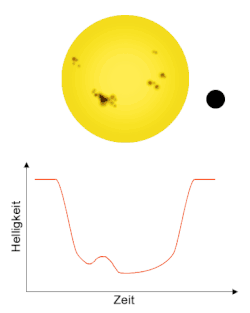
Sternenflecke, die vom Planet während eines Transits bedeckt werden, sind im Helligkeitsverlauf erkennbar.

Von Inhomogenitäten im Magnetfeld des Sternes werden bei gebündeltem Austreten von Feldlinien aus der Sternenoberfläche Sternenflecken verursacht. Diese erscheinen dunkler und reduzieren, ebenso wie ein Transit, die Helligkeit des Sterns. Ist die Bahnneigung eines Transitplaneten bekannt, ist sein Weg über die Sternenscheibe bekannt. Befindet sich auf dieser Linie ein Sternenfleck, bedeckt der Planet während seines Durchgangs ebenfalls den Fleck. Da der Fleck eine geringere Helligkeit als die ihn umgebende Oberfläche des Sterns aufweist, ist der gesamte Helligkeitsabfall bei verdecktem Fleck kleiner, als wenn der Planet und der Fleck sichtbar sind. Die Helligkeitskurve weist also bei Vorhandensein eines Sternenflecks auf dem Weg des Planeten eine Anhebung auf. Handelt es sich um einen Transitplaneten mit einer geringen Umlaufperiode im Bereich von wenigen Tagen, lässt sich diese Anhebung mehrfach beobachten, da Flecken auf dem Stern im Bereich von mehreren Tagen bis zu Wochen für einen Umlauf benötigen. Auch lässt sich eine Rotation des Sterns und eine Verschiebung des Flecks auf der Oberfläche des Sterns nachweisen, wenn die in der Helligkeitskurve sichtbare Anhebung im Laufe mehrerer Transits weiterwandert. Besitzt ein Stern Transitplaneten mit sehr geringer Umlaufdauer, können damit Daten über seine Sternenflecken gewonnen werden, indem möglichst viele Transits ausgewertet werden. Über die Häufigkeit des Auftretens und die Größe der beobachteten Sternenflecken sind Rückschlüsse über die magnetische Aktivität des Sterns möglich.[17][18][19]

Transit timing variation (TTV)

Mittels Transit timing variation ist es möglich, durch Beobachtung des Transits eines oder mehrerer Planeten in einem System auf die Existenz weiterer Planeten in diesem System zu schließen. Durch Bahnstörungen werden die Umlaufbahnen der Transitplaneten beeinflusst. Auch wenn der die Bahnstörungen verursachende Planet nicht durch einen Transit nachweisbar ist, lassen sich diese Beeinflussungen durch eine Veränderung der Umlaufzeit und damit des zeitlichen Abstands der Transits nachweisen. Durch Modellrechnungen lassen sich so diese Variationen im zeitlichen Abstand auf einen weiteren Himmelskörper in diesem Planetensystem zurückführen. Je länger ein Planetensystem beobachtet wird, umso genauer kann auf den zusätzlichen oder die zusätzlichen Planeten geschlossen werden. Auch können durch längere Beobachtungen die möglichen Parameter für den verursachenden Planeten eingeschränkt werden, sodass bei genügend langer und genauer Beobachtung grob die Bahn, die Phase und die Masse des Planeten bestimmt werden können, obwohl dieser nie einen Transit verursacht. Die Methode lässt es zu, dass selbst Nicht-Transitplaneten mit einer Masse ähnlich der der Erde nachweisbar sind.[20][21]

Trojaner

Mit der Transitmethode lassen sich Trojaner in anderen Planetensystemen nachweisen. Diese Anhäufungen von Asteroiden umkreisen im gleichen Orbit wie ein Planet den Stern und befinden sich in den Lagrange-Punkten L4 und L5. Werden viele Umläufe eines Planeten durchgängig beobachtet, lassen sich diese Helligkeitskurven übereinanderlegen und statistisch mitteln. Durch die erwartete große Anzahl an Asteroiden in den Lagrange-Punkten entsteht ein messbarer Helligkeitsabfall, der zwar in einem einzelnen Messprozess nicht vom Rauschen zu unterscheiden ist, sich aber bei Überlagerung vieler Messungen nachweisen lässt. Durch den Transit des Planeten, den die Trojaner begleiten, sind die Zeitpunkte, in denen die Trojaner vor dem Stern zu erwarten sind, berechenbar. Zu diesen Zeitpunkten kann darauf gezielt beobachtet werden.[22][23] Ebenso können Trojaner eines massereichen Planeten in Summe aller einzelnen Asteroiden dieses Gebietes eine Gesamtmasse eines kleinen Planeten wie Merkur oder Mars erreichen. Damit lassen sich bei Existenz eines anderen Planeten, dessen Transit beobachtbar ist, kleine Bahnstörungen und Variationen in der Umlaufzeit nachweisen. Diese Variationen in der Umlaufzeit ermöglichen Rückschlüsse auf Trojaner bei anderen Planeten im beobachteten Planetensystem.[24]

Exomonde

Besitzt ein Exoplanet einen oder mehrere Monde, so können diese Monde ebenfalls einen Helligkeitsabfall verursachen, der immer zur Zeit des Transits des Planeten stattfindet. Dieser Durchgang besitzt in der Regel eine geringere Transittiefe als jener des Planeten, lässt sich jedoch für große Monde nachweisen. Dadurch, dass der Mond seinen Planeten umkreist, wird bei mehreren beobachteten Transits dieser kleine zusätzliche Helligkeitsabfall jeweils einige Zeit früher oder später beginnen oder ganz ausfallen, je nachdem wo sich der Mond gerade auf seiner Umlaufbahn befindet. Werden genügend solcher Ereignisse beobachtet, lassen sich aus der zusätzlichen Transittiefe und aus der Beobachtung der jeweiligen Lage des Mondes relativ zum Planeten seine Größe und seine Umlaufperiode um seinen Planeten bestimmen.

Darüber hinaus besteht theoretisch die Möglichkeit die Masse des Mondes abzuschätzen: Da beide Körper um einen gemeinsamen Schwerpunkt kreisen, lassen sich aus den leicht unterschiedlichen Eintrittszeiten des Planeten in die Sternenscheibe das Massenverhältnis der beiden Körper bestimmen. Ist die Masse des Transitplaneten bekannt, folgt daraus die Masse des Mondes. Mithilfe der Transittiefe des Mondes lässt sich damit ebenfalls seine Dichte bestimmen.[25]

Siehe auch: Extrasolarer Mond

Anwendung der Transitmethode in unserem Sonnensystem

Mit einer abgewandelten Form der Transitmethode kann man auch in unserem Sonnensystem nach Himmelskörpern suchen, welche sich innerhalb der Erdbahn um die Sonne bewegen. Im 19. Jahrhundert wurde dies durchgeführt, um nach einem, von den damaligen Theorien postulierten, aber nicht existierenden intramerkuriellen Planeten zu suchen. Im Unterschied zur Transitmethode zur Untersuchung von Exoplaneten hielt man hierbei Ausschau nach kleinen punkt- oder scheibenförmigen Objekten, welche in einem Zeitraum von einigen Stunden über die Sonne wandern. Insbesondere für die Jagd nach Himmelskörpern in großer Sonnennähe ist ein derartiges Vorgehen sehr sinnvoll, weil derartige Objekte nur einen geringen Winkelabstand von der Sonne erreichen können und somit schon in der hellen Abenddämmerung untergehen bzw. erst in der hellen Morgendämmerung aufgehen, was eine Beobachtung hochgradig erschwert. Transite können hingegen von jedem Objekt, welches in die Sichtlinie zwischen einem Beobachter und der Sonne geraten und einen Winkeldurchmesser, der das Auflösungsvermögen des Beobachtungsinstruments übersteigt, beobachtet werden – unabhängig von der Entfernung des Objekts zur Sonne und vom Beobachter. Ein prinzipieller Nachteil dieser Methode ist, dass Transite von Objekten innerhalb der Erdbahn wegen der Bahnneigungen im Regelfall selten sein dürften (man denke an die Seltenheit von merkurtransiten und Venustransiten). Bis heute (2020) ist kein neues Objekt im Sonnensystem anhand eines Transits entdeckt worden.

Siehe auch

Durchgang

Trivia

Der 1999 entdeckte Planet HD 209458 b war der erste mit dieser Methode nachgewiesene Exoplanet.
Kepler-88 b war der erste Exoplanet, bei dem Unregelmäßigkeiten des Transits (transit timing variations) Hinweise auf den weiteren Exoplaneten Kepler-88c gaben.
Viele bis 2018 entdeckten Transitplaneten befinden sich in den Sternbildern Schwan und Leier.[26] Das Weltraumteleskop Kepler beobachtete dort einen Himmelsausschnitt und wies bis dahin die meisten Exoplaneten nach.
HD 189733 ist ein relativ heller Stern (7.676 mag), dessen Exoplanet HD 189733 b auch von Amateurastronomen nachgewiesen werden kann.[27]

Literatur

Mathias Scholz: Planetologie extrasolarer Planeten. Springer Spektrum, Springer-Verlag Berlin Heidelberg 2014, ISBN 978-3-642-41748-1, S. 112ff.
Valerio Bozza, Luigi Mancini, Alessandro Sozzetti: Methods of Detecting Exoplanets: 1st Advanced School on Exoplanetary Science. Springer, 2016, ISBN 978-3-319-27456-0.

Weblinks

interaktives Webapplet zur Simulation verschiedener Transitkurven (Adobe Flash)
Exoplanet-style transit light curve of Venus auf YouTube. Zeitrafferaufnahme des Venustransits 2012 mit Helligkeitskurve
Gibt es extrasolare Planeten? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 17. Jan. 1999. (kurze Erklärung der Methode gegen Ende der Episode)
Methoden der Exoplanetenentdeckung - Die Transitmethode. Artikel und Applet zur Simulation von Exoplanetentransits auf beltoforion.de.

Einzelnachweise

Exoplanet and Candidate Statistics. In: NASA Exoplanet Archive. Abgerufen am 4. August 2019.
Will all the stars Kepler observes have transiting planets? In: Kepler FAQ. (nasa.gov [abgerufen am 8. Juli 2016]).
Jeff Hecht: The truth about exoplanets. In: Nature. Band 503, 18. Februar 2016, S. 272–274, doi:10.1038/530272a.
Frequently Asked Questions from the Public about the Kepler Mission. (nasa.gov [abgerufen am 8. Juli 2016]).
Mathias Scholz: Planetologie extrasolarer Planeten. Springer Spektrum, Springer-Verlag Berlin Heidelberg 2014, ISBN 978-3-642-41748-1, S. 112–173.
exoplanets.org Histogramm der Umlaufdauer (orbital period) aller Transitplaneten (Filter: "Transit = 1") plottbar.
About Transits. In: About Kepler. (nasa.gov [abgerufen am 8. Juli 2016]).
Don’t the stars vary more than the change caused by a transit? In: Kepler FAQ. (nasa.gov [abgerufen am 8. Juli 2016]).
Valerio Bozza, Luigi Mancini, Alessandro Sozzetti: Methods of Detecting Exoplanets: 1st Advanced School on Exoplanetary Science. Springer, 2016, ISBN 978-3-319-27456-0, S. 117.
Do you need several transits to find a planet? In: Kepler FAQ. (nasa.gov [abgerufen am 8. Juli 2016]).
Radial Velocity: The First Method that Worked. (planetary.org [abgerufen am 8. Juli 2016]).
Atmospheres of exoplanets. (exoplanets.ch Homepage des Observatoire de Genève der Universität in Genf [abgerufen am 4. August 2019]).
Kurze Beschreibung der Methodik unter dem Menüpunkt der Transitmethode.(exoplanets.nasa.gov [abgerufen am 8. Juli 2016])
Bruce L. Gary: HAT-P-7: AXA Light Curves & Finder Charts & All-Sky Photometry Results (brucegary.net [abgerufen am 8. Juli 2016])
W. J. Borucki et al.: Kepler’s Optical Phase Curve of the Exoplanet HAT-P-7b. In: Science. Vol. 325, 7. August 2009, S. 709 f., doi:10.1126/science.1178312 (sciencemag.org).
Jason W. Barnes: Transit Lightcurves of Extrasolar Planets Orbiting Rapidly-Rotating Stars. In: The Astrophysical Journal. Band 705, Nr. 1, 2009, S. 683–692, doi:10.1088/0004-637X/705/1/683, arxiv:0909.1752.
Adriana Valio: Starspot detection from planetary transits observed by CoRoT. In: RevMexAA (Serie de Conferencias). 2009 (researchgate.net).
Jason A. Dittmann, Laird M. Close, Elizabeth M. Green, Mike Fenwick: A Tentative Detection of a Starspot During Consecutive Transits of an Extrasolar Planet from the Ground: No Evidence of a Double Transiting Planet System Around TrES-1. In: Astrophys.J. Band 701, 2009, S. 756–763, doi:10.1088/0004-637X/701/1/756, arxiv:0906.4320.
James R. A. Davenport, Leslie Hebb, Suzanne L. Hawley: Using Transiting Planets to Model Starspot Evolution. 2014, arxiv:1408.5201.
Jordi Miralda-Escudé: Orbital Perturbations of Transiting Planets: A Possible Method to Measure Stellar Quadrupoles and to Detect Earth-Mass Planets. In: The Astrophysical Journal. Band 564, Nr. 2, 2002, S. 1019–1023, doi:10.1086/324279.
Matthew J. Holman, Norman W. Murray: The Use of Transit Timing to Detect Extrasolar Planets with Masses as Small as Earth. In: Science. 2005, arxiv:astro-ph/0412028.
Markus Janson: A Systematic Search for Trojan Planets in the Kepler data. doi:10.1088/0004-637X/774/2/156, arxiv:1307.7161.
Michael Hippke, Daniel Angerhausen: A statistical search for a population of Exo-Trojans in the Kepler dataset. In: The Astrophysical Journal Letters. Band 811, Nr. 1, 2015, doi:10.1088/0004-637X/811/1/1, arxiv:1508.00427.
Eric B. Ford, Matthew J. Holman: Using Transit Timing Observations to Search for Trojans of Transiting Extrasolar Planets. In: The Astrophysical Journal Letters. Band 664, Nr. 1, 2007, S. L51–L54, doi:10.1086/520579, arxiv:0705.0356.
A. Simon, K. Szatmáry, and Gy. M. Szabó: Determination of the size, mass, and density of "exomoons" from photometric transit timing variations. In: Astronomy & Astrophysics. Band 470, Nr. 2, 2007, S. 727–731, doi:10.1051/0004-6361:20066560.
Kepler's Field Of View In Targeted Star Field nasa.gov
David Schneider: DIY Exoplanet Detector – You don’t need a high-powered telescope to spot the signature of an alien world. In: IEEE Spectrum. 28. November 2014, abgerufen am 18. Februar 2018.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[exoplanetstats-1] Exoplanet and Candidate Statistics. In: NASA Exoplanet Archive. Abgerufen am 4. August 2019.

[2] Will all the stars Kepler observes have transiting planets? In: Kepler FAQ. (nasa.gov [abgerufen am 8. Juli 2016]).

[nature-hecht-3] Jeff Hecht: The truth about exoplanets. In: Nature. Band 503, 18. Februar 2016, S. 272–274, doi:10.1038/530272a.

[keplerfaq-4] Frequently Asked Questions from the Public about the Kepler Mission. (nasa.gov [abgerufen am 8. Juli 2016]).

[scholz-5] Mathias Scholz: Planetologie extrasolarer Planeten. Springer Spektrum, Springer-Verlag Berlin Heidelberg 2014, ISBN 978-3-642-41748-1, S. 112–173.

[exoplanets.orgplots-6] xoplanets.org Histogramm der Umlaufdauer (orbital period) aller Transitplaneten (Filter: "Transit = 1") plottbar.

[keplerabouttransits-7] About Transits. In: About Kepler. (nasa.gov [abgerufen am 8. Juli 2016]).

[8] Don’t the stars vary more than the change caused by a transit? In: Kepler FAQ. (nasa.gov [abgerufen am 8. Juli 2016]).

[9] Valerio Bozza, Luigi Mancini, Alessandro Sozzetti: Methods of Detecting Exoplanets: 1st Advanced School on Exoplanetary Science. Springer, 2016, ISBN 978-3-319-27456-0, S. 117.

[10] Do you need several transits to find a planet? In: Kepler FAQ. (nasa.gov [abgerufen am 8. Juli 2016]).

[plansoc-11] Radial Velocity: The First Method that Worked. (planetary.org [abgerufen am 8. Juli 2016]).

[12] Atmospheres of exoplanets. (exoplanets.ch Homepage des Observatoire de Genève der Universität in Genf [abgerufen am 4. August 2019]).

[13] Kurze Beschreibung der Methodik unter dem Menüpunkt der Transitmethode.(exoplanets.nasa.gov [abgerufen am 8. Juli 2016])

[14] Bruce L. Gary: HAT-P-7: AXA Light Curves & Finder Charts & All-Sky Photometry Results (brucegary.net [abgerufen am 8. Juli 2016])

[15] W. J. Borucki et al.: Kepler’s Optical Phase Curve of the Exoplanet HAT-P-7b. In: Science. Vol. 325, 7. August 2009, S. 709 f., doi:10.1126/science.1178312 (sciencemag.org).

[barnes-16] Jason W. Barnes: Transit Lightcurves of Extrasolar Planets Orbiting Rapidly-Rotating Stars. In: The Astrophysical Journal. Band 705, Nr. 1, 2009, S. 683–692, doi:10.1088/0004-637X/705/1/683, arxiv:0909.1752.

[17] Adriana Valio: Starspot detection from planetary transits observed by CoRoT. In: RevMexAA (Serie de Conferencias). 2009 (researchgate.net).

[18] Jason A. Dittmann, Laird M. Close, Elizabeth M. Green, Mike Fenwick: A Tentative Detection of a Starspot During Consecutive Transits of an Extrasolar Planet from the Ground: No Evidence of a Double Transiting Planet System Around TrES-1. In: Astrophys.J. Band 701, 2009, S. 756–763, doi:10.1088/0004-637X/701/1/756, arxiv:0906.4320.

[19] James R. A. Davenport, Leslie Hebb, Suzanne L. Hawley: Using Transiting Planets to Model Starspot Evolution. 2014, arxiv:1408.5201.

[20] Jordi Miralda-Escudé: Orbital Perturbations of Transiting Planets: A Possible Method to Measure Stellar Quadrupoles and to Detect Earth-Mass Planets. In: The Astrophysical Journal. Band 564, Nr. 2, 2002, S. 1019–1023, doi:10.1086/324279.

[21] Matthew J. Holman, Norman W. Murray: The Use of Transit Timing to Detect Extrasolar Planets with Masses as Small as Earth. In: Science. 2005, arxiv:astro-ph/0412028.

[22] Markus Janson: A Systematic Search for Trojan Planets in the Kepler data. doi:10.1088/0004-637X/774/2/156, arxiv:1307.7161.

[23] Michael Hippke, Daniel Angerhausen: A statistical search for a population of Exo-Trojans in the Kepler dataset. In: The Astrophysical Journal Letters. Band 811, Nr. 1, 2015, doi:10.1088/0004-637X/811/1/1, arxiv:1508.00427.

[24] Eric B. Ford, Matthew J. Holman: Using Transit Timing Observations to Search for Trojans of Transiting Extrasolar Planets. In: The Astrophysical Journal Letters. Band 664, Nr. 1, 2007, S. L51–L54, doi:10.1086/520579, arxiv:0705.0356.

[25] A. Simon, K. Szatmáry, and Gy. M. Szabó: Determination of the size, mass, and density of "exomoons" from photometric transit timing variations. In: Astronomy & Astrophysics. Band 470, Nr. 2, 2007, S. 727–731, doi:10.1051/0004-6361:20066560.

[26] Kepler's Field Of View In Targeted Star Field nasa.gov

[27] David Schneider: DIY Exoplanet Detector – You don’t need a high-powered telescope to spot the signature of an alien world. In: IEEE Spectrum. 28. November 2014, abgerufen am 18. Februar 2018.