Tag-Nacht-Grenze

Die Tag-Nacht-Grenze ist die Grenze zwischen der durch einen Stern wie die Sonne angestrahlten Lichtseite und der unbeleuchteten Schattenseite eines Himmelskörpers, insbesondere eines Planeten oder Mondes. Der Anblick dieser Licht-Schatten-Grenze wird in der Astronomie und Meteorologie auch Terminator (lat. ‚Abgrenzer‘) oder Separator (lat. ‚Trenner‘) genannt. In der Funktechnik, insbesondere beim Amateurfunk, wird die Tag-Nacht-Grenze auch als Greyline (deutsch wörtlich „graue Linie“) bezeichnet.

Erde und Mond beide ungefähr zur Dichotomie (halbe Phase bei Phasenwinkel 90°; Bild aufgenommen von der Raumsonde Galileo [NASA])

Die Sonne von der Tag-Nacht-Grenze aus gesehen (Sonnenaufgang über dem Hoggar im Süden Algeriens)

Die Lage des Terminators in Bezug auf einen Betrachter ergibt sich aus dem Phasenwinkel und bestimmt die Phase des Himmelskörpers, seine Lichtgestalt für den Betrachter. So heißen die Mondphasen bei den Phasenwinkeln 0°, 90° und 180° Voll-, Halb- bzw. Neumond.

Grundlagen

Ursache und Aussehen

Studie der Mondsichel von Leonardo da Vinci, Rötel, vor 1510

Beleuchtet eine Lichtquelle einen Körper, so liegen alle Bereiche seiner Oberfläche im Schatten, die vom Licht nicht direkt erreicht werden. Nimmt man zur Vereinfachung an, dass parallele Lichtstrahlen auf eine Kugel treffen, so wird dadurch die Kugel in eine im Licht und eine im Schatten liegende Halbkugel geteilt. Die Trennungslinie bildet einen Großkreis. Dieser erscheint durch seine räumliche Lage und die perspektivische Verzerrung im Allgemeinen als eine halbe Ellipse, deren andere Hälfte auf der Rückseite des Körpers liegt. Bei besonderen Betrachtungswinkeln erscheint die trennende Linie als Gerade oder als Kreis.

Das bekannteste Beispiel einer solchen Grenzlinie zwischen der Licht- und Schattenseite eines Himmelskörpers ist die Innenseite der Mondsichel, die ihre Gestalt mit den Mondphasen ändert. Leonardo da Vinci beschrieb die Natur des Mondlichts als von der Mondkugel reflektiertes Sonnenlicht – und damit auch diese Linie – mit den Worten:

„Der Mond hat kein Licht von sich aus,
und soviel die Sonne von ihm sieht, so viel beleuchtet sie;
und von dieser Beleuchtung sehen wir so viel, wie viel davon uns sieht“

– Leonardo da Vinci[1]

Auch auf der Erde gibt es einen solchen Terminator, der die von der Sonne beschienene Seite von der dunklen Nachtseite trennt. Hier gibt es jedoch zusätzlich Zeitspannen, in denen die Sonne knapp unter dem Horizont ist, an denen aber durch die Streuung des Sonnenlichts in der Erdatmosphäre der Himmel noch hell ist, die Dämmerung. Durch sie ist die Tag-Nacht-Grenze der Erde, von außerhalb betrachtet, keine scharfe Linie, sondern hat eine deutliche Unschärfe. Sie ist nachtseitig zu einer Zone mit einer Breite von bis zu einigen hundert Kilometern, der Dämmerungszone, verstrichen.

Auf dem Mond gibt es keine Atmosphäre und deshalb auch keine Dämmerung. Wenn dort die Sonne untergegangen ist, wird es schlagartig dunkel. Der Terminator des Mondes zeigt so scharfe Licht-Schatten-Grenzen auf dem Oberflächenrelief. Eine gewisse Unschärfe des Terminators gibt es jedoch auch durch die Rauigkeit des Geländes, sowie dadurch, dass die Lichtquelle (die Sonne) nicht punktförmig ist und somit ihre Lichtstärke während des Sonnenauf- und -untergangs allmählich zu- und abnimmt. Letzterer Effekt ist bei sonnennahen Körpern wie dem Merkur am stärksten, weil von diesen Körpern aus der scheinbare Durchmesser der Sonne am größten ist.

Bewegung und Bedeutung

Dadurch, dass der Himmelskörper sein Zentralgestirn auf einer bestimmten Umlaufbahn umkreist und dabei eine bestimmte Eigenrotation (mit einer bestimmten Achsneigung zur Ebene der Umlaufbahn) ausführt, bewegt sich die Tag-Nacht-Grenze in einer bestimmten Weise über die Oberfläche des Himmelskörpers. Sie zeigt dabei an, wo es auf der Oberfläche des Himmelskörpers gerade Lichter Tag oder Nacht ist. Durch den Durchgang der Tag-Nacht-Grenze durch einen gegebenen Ort ist für diesen Ort Anfang und Ende des lichten Tages und damit auch die jeweilige Tageslänge und Sonnenscheindauer definiert.

Auf der Erde verschiebt sich die Tag-Nacht-Grenze in Äquatornähe mit ungefähr 1.670 km/h gen Westen und erreicht nach etwa 24 Stunden wieder die gleiche Stellung am selben Ort. Die Zeitspanne für diesen einen Zyklus aus Tag und Nacht ist für alle Orte auf der Erde gleich, wenn sie nicht in den Polarregionen liegen. Durch die Neigung der Erdachse gegen die Ekliptik kann es in den geographischen Breiten jenseits der Polarkreise vorkommen, dass während 24 Stunden kein Wechsel zwischen Tag und Nacht stattfindet – weil die Tag-Nacht-Grenze den Ort nicht passiert. Es herrscht dann Polartag oder Polarnacht.

Bildbeispiele

Der Terminator auf dem Merkur
Terminator des Mondes (Erdmond) –
Details von Relief mit Kratern
Doppelter Terminator auf Mimas (Saturnmond I) – oben solarer Terminator, rechts durch Widerschein (indirektes Sonnenlicht) des Saturn
Terminator des Titan (Saturnmond VI) – unscharfe Zone sowie Aufscheinen seiner Atmosphäre.
Cassini, April 2007

Phasenwinkel Φ und Phase k

Abhängig von dem Winkel, den Lichtquelle und Beobachter in Bezug auf den beleuchteten Himmelskörper bilden, wird ein unterschiedlich großer Teil von dessen beleuchteter Hälfte für den Beobachter sichtbar als Lichtgestalt einer bestimmten Phase. Dieser Zusammenhang lässt sich mathematisch beschreiben über den Winkel im Raum, den Phasenwinkel, und auch über den sichtbaren Anteil der beleuchteten Scheibenfläche, die Phase.

Wenn der Beobachter am Ort der Lichtquelle stünde oder auf der Linie der Projektionsachse, so wäre der Phasenwinkel gleich 0°, er sähe dann genau auf die beleuchtete Hälfte, die Scheibe erschiene vollständig beleuchtet (beleuchteter Anteil also 1 von 1 oder 1/1), somit wäre die Phase gleich 1 und würde „volle Phase“ genannt, beispielsweise Vollmond für den Mond.

Neumond dagegen oder „neue Phase“ ist Phase gleich 0 (Anteil 0/1 oder 0 von 1), somit kein Teil der Scheibe beleuchtet, der Beobachter sieht also genau auf die unbeleuchtete Hälfte und steht so zur Lichtquelle, dass der Himmelskörper exakt auf einer Linie dazwischen liegt, der Phasenwinkel beträgt nun 180°.

Der Phasenwinkel wird also gemessen zwischen Lichtquelle Sonne (S) und Beobachter (B) bezogen auf den Himmelskörper als Objekt (O) im Scheitelpunkt – vom Objekt aus gesehen ist es der Winkel, unter dem S und B erscheinen:[2]

\Phi =\sphericalangle {\overline {OS}}\,{\overline {OB}}

Wenn bei Betrachtung eines entfernten Objektes die Abstandswerte bekannt sind, lässt sich der Phasenwinkel daraus errechnen:[2]

\Phi =\arccos \;{\frac {r^{2}+\Delta ^{2}-R^{2}}{2\cdot r\cdot \Delta }}

mit (beleuchtet)

0^{\circ }<\Phi <180^{\circ }

(unbeleuchtet)

Dabei sei:

R

… Abstand vom Baryzentrum/Lichtquelle zum Beobachter

r

… Abstand vom Baryzentrum/Lichtquelle zum Objekt

\Delta

… Abstand vom Beobachter zum Objekt

Über den Phasenwinkel lassen sich sowohl Terminator als auch Phase angeben.

Die Phase kann daneben wie schon erwähnt auch als der beleuchtete Anteil der scheinbaren Gesamtfläche wiedergegeben werden, beziehungsweise als Beleuchtungsdefekt aufgefasst werden:[2]

k=\arccos \;{\frac {(r^{2}+\Delta )^{2}-R^{2}}{4\cdot r\cdot \Delta }}

mit (beleuchtet)

1>k>0

(unbeleuchtet)

Der Phasenwinkel ist nur dann exakt 0° oder exakt 180°, wenn die drei Objekte genau auf einer Linie liegen. Da dies aber praktisch nicht vorkommt, erreicht der Phasenwinkel nur minimale Werte nahe bei 0° oder maximale von nahezu 180°.

Bei Vernachlässigung von Neigung und Exzentrizität der Bahn entspricht der hier besprochene geometrische Phasenwinkel $\Phi$ (ergänzt um ein Vorzeichen für einen Wertebereich von −180° bis +180°) dem Phasenwinkel $\omega t$ zur Beschreibung des periodischen Vorgangs.

Phasenwinkel und Elongation

Der Phasenwinkel liegt der Sichtlinie vom Himmelskörper zum Beobachter an und entspricht jener Elongation, unter der vom Objekt aus betrachtet der Beobachter gesehen würde.[3] Die vom Beobachter aus gesehene Elongation hingegen – also der Winkel, unter dem Objekt und Lichtquelle für ihn erscheinen – bestimmt nicht die Phase, sondern wird gebraucht, um den scheinbaren Abstand vom anstrahlenden Stern zum Himmelskörper und dessen Sichtbarkeit zu berechnen.[4] Im Besonderen kann bei Phasenwinkeln nahe 180° – und damit ja sehr geringer Elongation für den Beobachter – ein Durchgang oder eine Okkultation eintreten.

Hauptphasen und Phasenzyklus

Lichtgestalt der Erde im Jahreslauf oder Erdphasen für einen heliozentrisch ortsfesten Beobachter im Weltall (nicht größengetreue Darstellung)

Die Phasen hängen ab von der jeweiligen Stellung des Beobachters zum Himmelskörper wie zur Sonne als deren Konstellation und können regelmäßig aufeinanderfolgen in einem Zyklus; die auf den Beobachtungsort bezogene Dauer eines ganzen Phasen-Zyklus wird synodische Periode genannt.

In Abhängigkeit vom Phasenwinkel zeigen sich unterschiedliche Phasen, die nach ihrer Lichtgestalt benannt werden; die folgenden werden auch als Hauptphasen bezeichnet und stellen besondere Konstellationen dar (wie die Syszygien als Stellungen in gemeinsamer Ebene oder auf gleicher Linie).[4]

Volle Phase, $\Phi _{\mathrm {min} }=0^{\circ }:$ Stehen von dem Himmelskörper aus gesehen Sonne und Beobachter in derselben Richtung in einer Ebene, so sieht der Beobachter nur die Tagseite des Himmelskörpers und der Terminator fällt auf den Außenrand der gesehenen Scheibe. Diese Phase wird als voll bezeichnet. Für einen Beobachter auf der Erde stehen dann beispielsweise innere Planeten in oberer Konjunktion, äußere Planeten entweder in Konjunktion oder in Opposition, der Mond in Opposition.
Halbe Phase, $\Phi =90^{\circ }:$ Bei einem Phasenwinkel von 90° erblickt der Beobachter den Terminator so, dass dieser als Gerade erscheint. Die Scheibe wird anscheinend in zwei Hälften geschieden, eine halbkreisförmige Tagseite und eine ebensolche Nachtseite. Diese Phase wird auch Halbphase oder Dichotomie (dĭchŏtŏmos ‚entzweigeschnitten‘) genannt; sie tritt bei den äußeren Planeten nicht auf. Diese Stellung ist nicht zu verwechseln mit der Quadratur.
Neue Phase, $\Phi _{\mathrm {max} }=180^{\circ }:$ Wenn der Phasenwinkel nahezu maximal ist, stehen Himmelskörper und Sonne vom Beobachter aus gesehen in derselben Richtung in einer Ebene. Innere Planeten stehen dann in unterer Konjunktion, die anderen Planeten und der Mond in Konjunktion, zwischen Sonne und Beobachter; sie kehren ihm so ihre Nachtseite zu. Die (ekliptikale) Elongation beim Beobachter ist dann 0, daher bildet diese Phase im Fachgebrauch üblicherweise den Nullpunkt zur Berechnung von synodischen Perioden. Diese Phase heißt nur in Bezug auf den Mond Neu- und bleibt sonst unbenannt; sie ist nur möglich, wenn der Himmelskörper zwischen Beobachter und Lichtquelle tritt, wie der Erdmond oder innere Planeten. Das Präfix ‚Neu-‘ wird ansonsten nur noch bei der Bezeichnung Neulicht gebraucht, für die schmale Mondsichel etwa anderthalb Tage nach Neumond.

Zwischen diesen Hauptphasen hat der Terminator die Form eines Ellipsenbogens und gibt der Lichtgestalt die bekannte Sichelform oder einen fälschlich als „eiförmig“ bezeichneten Umriss, sowohl vor der vollen Phase (hin zunehmend) als auch nach der vollen Phase (her abnehmend) innerhalb eines Phasenzyklus.

Die Phase wird üblicherweise geozentrisch-ekliptikal angegeben: Die Zeiten für die wahre Beobachtung auf der Erdoberfläche weichen jeweils leicht davon ab, auch für den exakten Termin $\Phi _{\mathrm {max} }$ des Mondes, Neumond.

Geometrische Figur des Terminators

Auf einem kugelförmigen Körper bildet die Projektion von Licht eine runde Fläche, deren Rand ein Kreis ist. Dessen Durchmesser wird bei punktförmiger Lichtquelle mit wachsendem Abstand zum Körper größer und würde im Grenzfall unendlicher Entfernung – mit parallel einfallenden Strahlen ohne Ablenkung – am größten sein, der eines sogenannten Großkreises. Damit wäre die belichtete Hälfte der Kugeloberfläche von einer ebenso großen unbelichteten Hemisphäre abgesetzt. Die gleiche Teilung käme auch zustande bei einer flächigen Lichtquelle, die rechtwinklig abstrahlt und als Scheibe mit gleichem Radius wie der Körper in rechtem Winkel zu diesem steht – egal in welcher Entfernung. Die tatsächlichen Projektionsbedingungen können jeweils als Näherung an diese idealen Fälle verstanden werden und der Einfall von Lichtstrahlen dann vereinfacht als annähernd parallel.

Bei Himmelskörpern ohne Atmosphäre wird Licht weder beim Einfall noch nach der Reflexion abgelenkt und so auf einem kugelförmigen Körper eine Fläche mit kreisförmiger Begrenzung angestrahlt, von der reflektiertes Licht dann ein Bild entwirft als Anblick des Körpers, in der Astronomie auch Scheibe[2] (englisch disk) genannt.

Abhängig von dem Abstand des Beobachters und dem Winkel, unter dem die beleuchtete Halbkugel gesehen wird, erscheint auf deren Bild die Begrenzungslinie – der Terminator – nun je nach Phase als Kreis, als Ellipsenbogen, als Gerade oder gar nicht. Der Scheibenrand als äußerer Umfang der Scheibe und der Terminator als innere Aufteilung der Scheibenfläche bestimmen zusammen die Lichtgestalt eines beleuchteten Himmelskörpers, seinen Anblick oder Aspekt. Je nach Perspektive beziehungsweise Phase erscheint die Scheibe voll, halb oder nicht beleuchtet, wenn der Terminator vom elliptischen Bogen nun zum Kreis wird oder zur Geraden oder aber unsichtbar. Die Hauptachse jener Ellipse, als deren Bogen der Terminator erscheint, ist gleich dem scheinbaren Durchmesser $d$ der Scheibe, die kleine Halbachse errechnet sich näherungsweise zu $d\cdot k$ .

Dass eine feine Mondsichel manchmal hörnchenfömig wirkt, zur Luna cornuta wird, als seien die Spitzen nach innen gebogen, liegt an Überstrahlungseffekten (Irradiation) und der Überhöhung von Kontrasten durch unsere visuelle Wahrnehmung; so wird die helle schmale Mondgestalt überzeichnet abgehoben von ihrer verschieden dunklen Umgebung, einerseits dem nachtschwarzen Hintergrund, andererseits dem von Erdschein schwach beleuchteten Anteil des Mondes. Zudem wird das Mondlicht noch auf dem Weg durch die Erdatmosphäre gestreut. Die Hörnchenform der Erdsichel auf einigen Aufnahmen aus dem Weltraum kommt vor allem durch Brechungs- und Streuungseffekte zustande – so erscheinen aus dem All die schneebedeckten polaren Zonen aufgehellt und als verlängerte Spitzen. Stärker noch wird die Hörnchentäuschung bei der Venus, die zwar ebenfalls eine Atmosphäre hat, deren dunkle Seite aber immer unsichtbar bleibt, weil sie keinerlei Widerschein eines nahen Himmelskörpers erhält.[5]

Keine ellipsenförmige Begrenzung, keine Phase, sondern: Mondfinsternis 3. März 2007, Eintritt in Kernschatten der Erde

Die ideale Schattengrenze kann wie folgt berechnet werden (Programmcode: C):

xscale = cos(2 * PI * ph)
for (i = 0; i < RADIUS; i++) {
	cp = RADIUS * cos(asin((double) i / RADIUS));
	if (ph < 0.5) {
		rx = (int) (CENTER + cp);
		lx = (int) (CENTER + xscale * cp);
	} else {
		lx = (int) (CENTER - cp);
		rx = (int) (CENTER - xscale * cp);
	}
}

Weltkarte mit Tag-Nacht-Grenze, kurz nach der (nördlichen) Frühlings-Tagundnachtgleiche: Am Nordpol herrscht schon Polartag.

[rx, i] … Koordinaten des dunklen Scheibenrands
[lx, i] … Koordinaten des Terminators
als kartesische Koordinaten (hier: ganzzahlig pixelweise)
mit:

ph ……… Phase

RADIUS … Radius der Scheibe

CENTER … x-Koordinate des Scheibenmittelpunkts

Quelle: J. Walker’s Moontool,[6] nach Meeus[7] /Duffett-Smith[8]

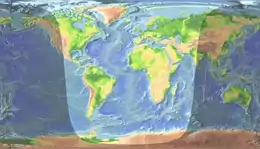
Mit der Projektion auf eine Karte nimmt der Terminator oder Separator dann komplexere Formen an. Auf eine Plattkarte projiziert zeigt die Licht-Schatten-Grenzlinie einen bogigen Verlauf etwa in Form einer verzerrten Sinus-Kurve und kann zu dem Termin der Tagundnachtgleiche in zwei parallele Linien zerfallen.

Im Übrigen sind die tatsächlichen Verhältnisse zu berücksichtigen, unter denen die Tag-Nacht-Grenze doch nur annähernd einen Großkreis bildet beziehungsweise der Terminator eine Ellipse mit großer Halbachse von nur nahezu dessen Radius: Denn die von einer punktförmigen Quelle ausgehenden Strahlen beleuchten nicht ganz die eine Hälfte einer Kugel, Brechungen in einer Atmosphäre verlagern die Grenzlinie, Streuungen machen sie unscharf, und flächige Ausdehnungen der Lichtquelle – wie der Sonne − führen zum Einfall von Licht aus verschiedenen Winkeln beziehungsweise können mehr beleuchten als exakt eine Halbkugel. Für allgemeine astronomische Betrachtungen dürfen aber Lichtstrahlen von der Sonne wegen des großen Abstandes verglichen mit dem Durchmesser der beleuchteten Himmelskörper als parallel einfallend angenommen werden.

Himmelsmechanische Zusammenhänge

Ein Stern hebt auf dem angestrahlten Himmelskörper eine Seite im Licht hervor und ab von der im Schatten. Die Abgrenzung von Licht- und Schattenseite wird abhängig vom Ort des Beobachters unter zwei grundsätzlich verschiedenen Blickwinkeln betrachtet:

In der Außenperspektive, das reflektierte Licht eines beleuchteten Himmelskörpers beobachtend, wird die Licht-Schatten-Grenze zum Terminator, der die Erscheinungsform der Lichtgestalt bestimmt. Innerhalb des Scheibenumfanges setzt er hell von dunkel ab und markiert so die Phase. Dieser Anblick hängt ab von dem Raumwinkel, den Stern und Himmelskörper in Bezug auf den Beobachtungsort bilden, beispielsweise Sonne und Mond zu Erde. Bei deren Rotationen um die eigene Achse ändert sich dieser Winkel fast nicht, wohl aber bei den Bewegungen von Mond und von Erde als Lauf um die Sonne. Die dadurch veränderte Phase zeigt sich auf der betrachteten Mondscheibe als Verlagerung des Terminators. Eine fortlaufende Reihe solcher Phasenänderungen bis zur Wiederholung bildet einen Phasen-Zyklus, der in diesem Fall auch Monat heißt.

In der Binnenperspektive, so auf der Oberfläche des angestrahlten Himmelskörpers der Lichtquelle unmittelbar exponiert, wird die Grenze zwischen Licht und Schatten zur Tag-Nacht-Grenze, die für einen Ort der Oberfläche bestimmt, ob er belichtet wird und direktes Licht den Boden erreichen kann. Dort mögen Formen leben, deren Aktivität durch Lichtenergie beeinflusst wird – sei es, dass sie der schädigenden Wirkung ausweichen oder dass sie energetische Effekte für sich nutzbar machen. Ob für jene Tag oder Nacht ist, hängt ab von dem Winkel, den Stern und Oberfläche des Himmelskörpers bilden in Bezug auf den Standort des Beobachters. Auf der Erde wäre es beispielsweise der Stand der Sonne über dem Meeresspiegel an einem Strand. Während der Umlaufbewegung der Erde im Orbit ändert sich dieser Winkel, und auch bei ihrer Drehung um die eigene Achse. Auf der Erdoberfläche wird dadurch die Tag-Nacht-Grenze verschoben; die fortgesetzte Verschiebung mit zweimaligem Wechsel zwischen hell und dunkel bis hin zu der Wiederholung einer ähnlichen Belichtungsphase am gleichen Ort bildet dann einen ganzen Tag-Nacht-Zyklus, der auch als voller Tag bezeichnet wird.

Die Tag-Nacht-Grenze kann sich verschieben, wenn der Körper in Bewegung ist. Liefe er dabei um die Lichtquelle ohne eigene Rotation, so bewegte sich die Licht-Schatten-Grenze während eines vollen Umlaufes zwei Mal über seine Oberfläche. Für einen stationären Beobachter auf diesem Körper wäre dann ein Tag-Nacht-Zyklus abgelaufen, der eben solange wie ein Jahr auf dieser Bahn dauerte. Angenommen, der Körper würde nun während einer Umlaufperiode genau einmal um sich selbst rotieren – und dies um eine Achse, die im rechten Winkel zur Bahnebene steht – so gibt es zwei Möglichkeiten: Dreht er sich in demselben Sinn, mit dem er umläuft, dann wendet er der umlaufenen Lichtquelle dauernd die gleiche Seite zu. Bei einer solchen gebundenen Rotation dauert sein Tag also wenn nicht ewig, dann so lange, bis der Stern als Lichtquelle erlischt – falls der Körper dann noch existiert. Dreht er sich jedoch im Gegensinn zur Umlaufrichtung, dann besteht sein Jahr aus zwei Tagen (und zwei Nächten).
Je nachdem also, ob für einen Körper die Eigenrotationsrichtung mit der Umlaufrichtung im Orbit übereinstimmt oder nicht, kann für eine orbitale Periode, in seinem Jahr, entweder ein Tag wegfallen oder ein Tag dazukommen. Anders ausgedrückt: Die Anzahl vollständiger Eigenumdrehungen ist nie gleich der Zahl an Tagen bezogen auf das Zentralgestirn, sondern entweder plus oder minus 1 innerhalb eines Jahres. Im Fall der Erde heißt das, dass ein Sonnentag nicht einer ganzen Rotationsperiode entspricht, sondern etwa 1/365 daran fehlt.

Wenn die Rotationsachse des Himmelskörpers exakt senkrecht auf seiner Bahnebene stünde, also mit einer Inklination gleich 0, so verliefe die Tag-Nacht-Grenze genau durch beide Pole. In diesem Fall gäbe es hinsichtlich der geographischen Breite auf diesem Himmelskörpers keinen Unterschied in der Zeitspanne von Tag oder Nacht, denn innerhalb eines Sonnentages wäre für alle Orte die Tag-Nacht-Grenze zweimal überschritten.
Wenn die Rotationsachse aber nicht genau senkrecht auf der Bahnebene des Himmelskörpers steht, ändern sich die Zeitspannen von lichtem Tag beziehungsweise Nacht von einem Tag-Nacht-Zyklus zum nächsten. Je weiter ein Ort vom Äquator entfernt liegt, desto größer werden die Unterschiede, die während eines Laufes um die Sonne auftreten. Um die Pole herum gibt es dann sogar Bereiche der Oberfläche, innerhalb deren die Tag-Nacht-Grenze bei manchen Rotationsperioden gar nicht überschritten wird. Die Grenzen dieser Gebiete definieren die Polarkreise.

Terminator der Erde

Unschärfe des Erdterminators
aus ISS, Flughöhe etwa 390 km (211 NM)

Auf dem Weg durch die Erdatmosphäre wird Licht gebrochen und gestreut, sodass es infolge der Brechung (Refraktion) um etwa einen halben Grad einen weiteren Bereich der Erdoberfläche erreicht und wegen seiner Streuung daneben Dämmerungszonen auftreten. Die Licht-Schatten-Grenze auf der Erdkugel fasst also tagseitig einen größeren Bereich als nachtseitig und ist zudem nachtseits unscharf.

Ein Teil des Lichts wird von der belichteten Erdoberfläche zurückgeworfen (Reflexion), als diffuse Rückstrahlung – je nach Oberflächenbeschaffenheit und Einfallswinkel ein unterschiedlich großer Anteil. Diese Albedo der Erde beträgt insgesamt zurzeit etwa ein Drittel (ca. 31 %) des einfallenden Sonnenlichtes, mit erheblichen Unterschieden im Rückstrahlvermögen zum Beispiel von Neuschneedecken (ca. 85 %) und von Wasserspiegeln bei Winkeln über 45° (ca. 5 %). Das reflektierte Licht passiert die Atmosphäre dann ein zweites Mal mit Brechung und Streuung, bevor ein Bild der Tag-Nacht-Grenze entworfen wird als Terminator auf der Erdscheibe – gesehen von außen mit Perspektive aus dem All.

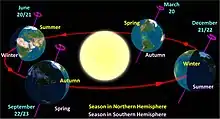
Die Rotationsachse der Erde steht nicht senkrecht zur Bahnebene, sondern in einem Winkel von etwa 66,5°, die Schiefe der Ekliptik beträgt damit etwa 23,5°. Während der Terminator einen Punkt am Äquator noch ziemlich genau alle 12 Stunden durchwandert, sodass lichter Tag und Nacht dort etwa gleich lange dauern, zeitigen schon in den gemäßigten Breiten die Auswirkungen der Ekliptikschiefe deutliche Unterschiede in den Längen von Tag und Nacht.

Zu den Sonnenwenden oder Solstitien sind im Sommer auf der nördlichen Halbkugel die lichten Tage am längsten (Sommersonnenwende, um den 21. Juni) – wie auf der südlichen Halbkugel dann die Nächte – und im Winter die Tage am kürzesten (Wintersonnenwende, um den 21. Dezember) – während auf der südlichen Hemisphäre dann der längste Tag ist. Jeweils ungefähr ein Vierteljahr nach diesen Terminen sind lichter Tag und Nacht gleich lang (Tagundnachtgleiche oder Äquinoktium, um den 20. März beziehungsweise um den 23. September). Die Tageslängen schwanken in mäßigen geographischen Breiten beispielsweise von 45° etwa zwischen 8 Stunden und 16 Stunden, entsprechend die Nachtlängen. Ab etwa 66,5° nördliche oder südliche Breite, den Polarkreisen, können dann Polartage mit Mitternachtssonne beziehungsweise die Polarnächte auftreten.

Gegen die Pole hin nimmt auch die Dauer der Dämmerung zu – sie beträgt schon bei 45° Breite bis zu anderthalb Stunden, als astronomische Dämmerung um die Wintersonnenwende; übertragen auf die Erdoberfläche entspricht dies einer Zone von über hundert Kilometern und die sogenannten weißen Nächte treten daher auch schon in Breiten unterhalb der Polarkreise auf.

Die vielfältigen Erscheinungen bei Untergang und Aufgang der Sonne entstehen als astronomische Phänomene durch Streuung und Brechung in jenen Schichten der Atmosphäre, die von der geometrischen Terminatorebene durchschnitten werden.

Erste Bilder von Mond und Erdsichel machte Lunar Orbiter 1 am 23. August 1966
Jahreszeitliche Schwankung der Tag-Nacht-Grenze, bezogen auf die Ekliptikalebene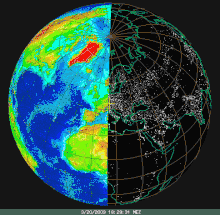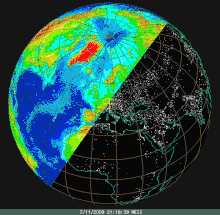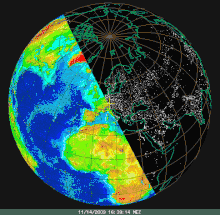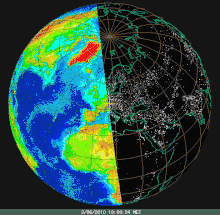
Tag-Nacht-Grenze von Sonnenuntergang im Jahreslauf, nun aber geostationär dargestellt für Zentraleuropa
Von der ISS in Ebene des Terminators aus gesehen erleuchtet gestreutes Licht die Erdatmosphäre[9]

Terminator des Mondes

Details am Terminator des Mondes

Wenn die Sonne untergegangen ist, wird es auf dem Mond schlagartig dunkel – doch dauert der Sonnenuntergang auf dem Mond durch dessen langsame Rotation etliche Stunden. Der Terminator aber bildet eine scharfe Linie. Von der Erde aus lässt sich die Wanderung der Tag-Nacht-Grenze des Mondes sehr gut verfolgen: Sie dauert einen Monat lang, eine Spanne der Mondphasen von Vollmond – abnehmendem Halbmond – Neumond – zunehmendem Halbmond – bis Vollmond. In diesem synodischen Mondmonat rückt der Terminator jede Nacht einige Grad vor (durchschnittlich mit ungefähr 12,6° in 24 h).

Dabei liegt die Schattenlinie des Mondes, die ungefähr rechtwinklig zur Ekliptik steht, von den mittleren geographischen Breiten der Erde aus gesehen zumeist so, dass der Mond jeweils nach links oder rechts ab- oder zuzunehmen scheint. Eine genau waagrecht zum Horizont liegende Mondsichel, auch Mondschiffchen genannt, kann von äquatornäheren Regionen unterhalb knapp 29° Breite aus zu sehen sein, wenn die Mondbahn senkrecht zum Horizont steht. Auch bei einem höheren Breitengrad mag die um gut 5° gegen die Ekliptik geneigte Bahnebene des Mondes noch relativ steile Stellungen zum Horizont erreichen – schwankend um rund 10° im Laufe von nahezu 19 Jahren und maximal zur großen Mondwende – doch keine senkrechten mehr und so erscheint eine liegende Mondsichel meistenfalls etwas gekippt. Nur sehr feine Sicheln können unter besonderen Bedingungen bei hoher ekliptischer Breite des Mondes waagrecht liegend gesehen werden.

Gegenüber Standorten der nördlichen Hemisphäre zeigt sich die Mondfigur bei gleicher Phase von der Südhalbkugel her betrachtet nun in umgekehrter horizontaler Orientierung – nicht wegen des Terminators, der nahezu dieselbe Lage hat, sondern weil der Beobachter gegenüber Beobachtern auf der Nordhalbkugel auf dem Kopf steht oder umgekehrt und beide die gleiche Lichtgestalt des Mondes je in ihrem topozentrischen Bezugssystem mit verschiedenem Zenit verorten. So scheint der abnehmende Mond dem Einen nach links und dem Anderen nach rechts zu weisen.

Eine häufige, dem Mondbeobachter geläufige Täuschung ist die, dass beispielsweise der Halbmond in Kulmination nicht genau auf die Sonne zu zeigen scheint, die dann knapp unter dem Horizont steht, sondern vermeintlich darüber weist: Die Verbindungsgerade Sonne–Mond scheint gekrümmt zu sein. Das ist ein Interpretationsirrtum. Tatsächlich handelt es sich um die Wirkung der Perspektive.[10]

Sofern der Phasenwinkel nicht exakt 0° wird, erscheint der Himmelskörper auch nicht vollständig erleuchtet. Der Mond etwa ist auch zu Vollmond nicht voll ausgeleuchtet, typische Werte liegen bei 99,96 %; nur bei kleinster ekliptikaler Breite – wie bei den Mondfinsternissen – würde er seiner maximal möglichen Ausleuchtung nahekommen, dann aber wird er ja durch den Erdschatten verfinstert und ist deshalb nicht voll beleuchtet.

Gerade noch sichtbare Mondsichel des aufgehenden, abnehmenden Mondes gut einen Tag vor Neumond kurz vor Sonnenaufgang

Auch die theoretisch sichtbare sehr schmale Sichel der Phase kurz vor oder nach Neumond ist tatsächlich nur schwer wahrzunehmen, weil der Mond dann sehr nahe bei der Sonne und so mit ihr am Taghimmel stehend überstrahlt wird – ausgenommen eine sehr kurze Zeitspanne in der Dämmerung. Beobachtbar ist die knapp über dem Horizont stehende feine Sichel des abnehmenden Mondes kurz vor Sonnenaufgang, die des zunehmenden kurz nach Sonnenuntergang. Die Sichtung der Mondsichel letztmals vor oder erstmals nach Neumond bildet die Basis mancher Uhrzeit- und Kalenderrechnung, so als Altlicht der altägyptischen und als Neulicht des heutigen islamischen Kalenders. Der sonnenabgewandte Teil des Mondes kann für uns sichtbar werden, da Reflexionen des Sonnenlichtes an der Erde und ihrer Atmosphäre, das Erdlicht, den Mond indirekt bescheinen und so auch die erdzugewandte Schattenseite des Mondes nicht ganz im Dunkeln lassen. Dass die Mondsichel unter Umständen als hörnchenförmig wahrgenommen werden kann, wird Luna cornuta genannt.[5]

Große Bedeutung hat der Terminator des Mondes für die Selenographie (Mondkartierung): Die gestochen scharfe Line zerfällt an ihrem Rand in zahlreiche Ränder der Krater und anderer Erhebungen, die an der Tag-Nacht-Grenze im Schattenbereich noch gerade beleuchtet sich als helle Bögen von der unbeleuchteten Mondoberfläche abheben oder aber schon in der Dunkelheit liegen und sich als Verdunklungen in der Tagseite abzeichnen. Bekannte Licht-Schatten-Effekte sind zum Beispiel der Goldene Henkel oder Lunar X.

Noch bis in die 2000er Jahre hinein waren genaue Zeichnungen der Schattenwürfe und deren Verzeichnung in Karten die einzige Möglichkeit, die dreidimensionale Topographie des Mondes zu ermitteln. Seit den Lunar-Orbiter-Missionen und der inzwischen hochauflösend möglichen photographischen Kartierung des Mondes arbeiten nur mehr Kreise engagierter Hobbyastronomen nach dieser Methode, um Detailfragen zu einzelnen Oberflächenformen zu klären.[11] Erst mit Sonden wie der chinesischen Chang’e-1 2007 und dem Lunar Reconnaissance Orbiter 2009, die mit Stereofotografie und Laserscanning für Altimetrie ausgerüstet wurden, ist die detailgetreue Mondtopographie nicht mehr von der visuellen Terminator-Beobachtung abhängig.

Detailphoto des Mondes (Mosaik aus 5 Aufnahmen) 10. Februar 2008, Frankreich
Dasselbe, überbelichtet: Deutlich erkennbar einige Abweichungen von der idealen Ellipsenform

Siehe auch: ComputerHotline - Lune-2008-05-14 – Durchgang des Mondes durch eine feststehende Kamera (ogg-video, 1:30)

Siehe auch

Weblinks

Wiktionary: Terminator – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Tag-Nacht-Grenze – Sammlung von Bildern, Videos und Audiodateien

World Sunlight Map. Zeigt die aktuelle Tag-Nacht-Grenze mit aktuellen Wolkenbildern. Auch in Mercator-, Mollweide-, Peters- und quadratischer Projektion.
John Walkers Earth and Moon Viewer zeigt die Tag- und Nachthälften auf einer Karte, einstellbar auf beliebige Zeiten und Koordinaten (Onlineversion von Home Planet).
Desktop Earth. Real-time Desktop Backgrounds. Automatisch aktualisierte Bilder der Tag-Nacht-Grenze als Desktop-Hintergrundbild.

Einzelnachweise

J. P. Richter: The Notebooks of Leonardo da Vinci. 1886, Abschnitt 896. Of the Moon, S. 157 (englisch, Gutenberg eText, sacred-texts.com)., della luna (italienisch/englisch). Abgerufen am 21. Februar 2011. Deutsch zitiert nach
Schlichting: Mondphasen im Apfelbaum. In: Spektrum der Wissenschaft. Nr. 9/10, S. 32.
Wolfgang Vollmann: Physische Wandelgestirn-Daten. In: Hermann Mucke (Hrsg.): Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. Zeiss Planetarium der Stadt Wien und Österreichischer Astronomischer Verein, Wien 1992, S. 185–196.
Vergleiche auch das angeführte Leonardo-Zitat, das in diesem Sinne als Merkspruch verstanden werden kann.
Norbert Pachner: Die Hauptstellungen der Wandelgestirne. Tafeln zur Abschätzung der Sichtbarkeitsverhältnisse. In: Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. S. 153–178 (veraltet, beruht noch auf Francou Bretagnon: VSOP 87).
Vgl. dazu: H. Joachim Schlichting: Mondphasen im Apfelbaum. In: Spektrum der Wissenschaft. Nr. 9/10, September 2010, S. 32 f. (spektrum.de).
Ders.: Warum die Sonne (k)ein Loch in die Welt brennt. In: Spektrum der Wissenschaft. Nr. 9/09, S. 38 f.
John Walker: mooncalc.c. Moontool for Windows – Astronomical Calculation Routines. In: Moontool/Homeplanet. Quellcode. 15. März 1999, Routine UPDATEICON – Update tray icon (englisch, Weblink siehe im Wikipedia-Artikel zum Programm).
Jean Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 1991, ISBN 0-943396-35-2 (englisch).
Peter Duffett-Smith: Practical Astronomy With Your Calculator. 3. Auflage. Cambridge University Press, Cambridge 1981, ISBN 0-521-28411-2 (englisch).
Vgl. auch: Datei:Sunset from the ISS.JPG, mit noch stärkerer Herauszeichnung der atmosphärischen Schichten.
Georg Glaeser und Karlheinz Schott: Geometric Considerations About Seemingly Wrong Tilt of Crescent Moon. In: KoG. Nr. 13, 2009 (englisch, srce.hr [abgerufen am 10. April 2019]). M. Wagenschein: Verstehen lehren. Beltz, Weinheim 1992, Verdunkelndes Wissen, S. 63. Zitiert in U. Backhaus: Von der Beobachtung astronomischer Phänomene zu eigenen Messungen. Koblenz, Einleitung, S. 2 (Online [PDF; 328 kB; abgerufen am 4. September 2021]). und in Ders.: Die Bewegung des Mondes. Vortragsmanuskript MNU-Tagung Bremerhaven. Hrsg.: Universität Duisburg-Essen. 14. November 2005, Abbildung 2: Sonne und Mond laufen im Laufe eines Tages gemeinsam über den Himmel, S. 3 (Online [PDF; 1,4 MB; abgerufen am 4. September 2021]).
Manfred Holl: Geschichte der Mondkarten. (Webbook) In: Astronomiehistorische Themen. Abgerufen im Jahr 2010.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[leo-1] J. P. Richter: The Notebooks of Leonardo da Vinci. 1886, Abschnitt 896. Of the Moon, S. 157 (englisch, Gutenberg eText, sacred-texts.com)., della luna (italienisch/englisch). Abgerufen am 21. Februar 2011. Deutsch zitiert nach
Schlichting: Mondphasen im Apfelbaum. In: Spektrum der Wissenschaft. Nr. 9/10, S. 32.

[Vollmann-2] Wolfgang Vollmann: Physische Wandelgestirn-Daten. In: Hermann Mucke (Hrsg.): Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. Zeiss Planetarium der Stadt Wien und Österreichischer Astronomischer Verein, Wien 1992, S. 185–196.

[Anm._Leo-3] Vergleiche auch das angeführte Leonardo-Zitat, das in diesem Sinne als Merkspruch verstanden werden kann.

[Pachner-4] Norbert Pachner: Die Hauptstellungen der Wandelgestirne. Tafeln zur Abschätzung der Sichtbarkeitsverhältnisse. In: Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. S. 153–178 (veraltet, beruht noch auf Francou Bretagnon: VSOP 87).

[Anm._Hörnchen-5] Vgl. dazu: H. Joachim Schlichting: Mondphasen im Apfelbaum. In: Spektrum der Wissenschaft. Nr. 9/10, September 2010, S. 32 f. (spektrum.de).
Ders.: Warum die Sonne (k)ein Loch in die Welt brennt. In: Spektrum der Wissenschaft. Nr. 9/09, S. 38 f.

[Walker-6] John Walker: mooncalc.c. Moontool for Windows – Astronomical Calculation Routines. In: Moontool/Homeplanet. Quellcode. 15. März 1999, Routine UPDATEICON – Update tray icon (englisch, Weblink siehe im Wikipedia-Artikel zum Programm).

[Meeus-7] Jean Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 1991, ISBN 0-943396-35-2 (englisch).

[Duffett-Smith-8] Peter Duffett-Smith: Practical Astronomy With Your Calculator. 3. Auflage. Cambridge University Press, Cambridge 1981, ISBN 0-521-28411-2 (englisch).

[Anm._Streuung-9] Vgl. auch: Datei:Sunset from the ISS.JPG, mit noch stärkerer Herauszeichnung der atmosphärischen Schichten.

[Backhaus-10] Georg Glaeser und Karlheinz Schott: Geometric Considerations About Seemingly Wrong Tilt of Crescent Moon. In: KoG. Nr. 13, 2009 (englisch, srce.hr [abgerufen am 10. April 2019]). M. Wagenschein: Verstehen lehren. Beltz, Weinheim 1992, Verdunkelndes Wissen, S. 63. Zitiert in U. Backhaus: Von der Beobachtung astronomischer Phänomene zu eigenen Messungen. Koblenz, Einleitung, S. 2 (Online [PDF; 328 kB; abgerufen am 4. September 2021]). und in Ders.: Die Bewegung des Mondes. Vortragsmanuskript MNU-Tagung Bremerhaven. Hrsg.: Universität Duisburg-Essen. 14. November 2005, Abbildung 2: Sonne und Mond laufen im Laufe eines Tages gemeinsam über den Himmel, S. 3 (Online [PDF; 1,4 MB; abgerufen am 4. September 2021]).

[Holl-11] Manfred Holl: Geschichte der Mondkarten. (Webbook) In: Astronomiehistorische Themen. Abgerufen im Jahr 2010.