Beurteilung eines binären Klassifikators

Bei einer Klassifizierung werden Objekte anhand von bestimmten Merkmalen durch einen Klassifikator in verschiedene Klassen eingeordnet. Der Klassifikator macht dabei im Allgemeinen Fehler, ordnet also in manchen Fällen ein Objekt einer falschen Klasse zu. Aus der relativen Häufigkeit dieser Fehler lassen sich quantitative Maße zur Beurteilung eines Klassifikators ableiten.

Häufig ist die Klassifikation binärer Natur, d. h., es gibt nur zwei mögliche Klassen. Die hier diskutierten Gütemaße beziehen sich ausschließlich auf diesen Fall. Solche binären Klassifikationen werden häufig in Form einer Ja/Nein-Frage formuliert: Leidet ein Patient an einer bestimmten Krankheit oder nicht? Ist ein Feuer ausgebrochen oder nicht? Nähert sich ein feindliches Flugzeug oder nicht? Bei Klassifikationen dieser Art gibt es zwei mögliche Arten von Fehlern: Ein Objekt wird der ersten Klasse zugeordnet, obwohl es der zweiten angehört, oder umgekehrt. Die hier beschriebenen Kennzahlen bieten dann eine Möglichkeit, die Zuverlässigkeit des zugehörigen Klassifikators (Diagnoseverfahren, Brandmelder, Fliegerradar) zu beurteilen.

Ja-Nein-Klassifikationen weisen Ähnlichkeiten zu statistischen Tests auf, bei denen zwischen einer Nullhypothese und einer Alternativhypothese entschieden wird.

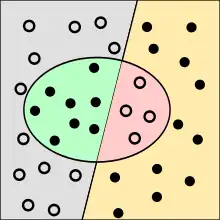
Wahrheitsmatrix: Richtige und falsche Klassifikationen

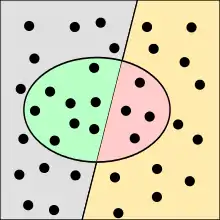
Ein Test soll kranke und gesunde Menschen voneinander unterscheiden. Jeder Mensch wird durch einen Punkt dargestellt, der links (krank) bzw. rechts (gesund) der schwarzen Linie liegt. Alle hier durch Punkte repräsentierte Menschen wurden getestet.
Die Punkte im Oval sind die von dem Test als krank klassifizierten Menschen. Richtig bewertete Fälle sind grün oder gelb, falsch bewertete rot oder grau unterlegt.

Um einen Klassifikator zu bewerten, muss man ihn in einer Reihe von Fällen anwenden, bei denen man zumindest im Nachhinein Kenntnis über die „wahre“ Klasse der jeweiligen Objekte hat. Ein Beispiel für so einen Fall ist ein medizinischer Labortest, mit dem festgestellt werden soll, ob eine Person eine bestimmte Krankheit hat. Später wird durch aufwändigere Untersuchungen festgestellt, ob die Person tatsächlich an dieser Krankheit leidet. Der Test stellt einen Klassifikator dar, der die Personen in die Kategorien „krank“ und „gesund“ einordnet. Da es sich um eine Ja/Nein-Frage handelt, sagt man auch, der Test fällt positiv (Einordnung „krank“) oder negativ (Einordnung „gesund“) aus. Um zu beurteilen, wie gut geeignet der Labortest für die Diagnose der Krankheit ist, wird nun bei jedem Patienten dessen tatsächlicher Gesundheitszustand mit dem Ergebnis des Tests verglichen. Dabei können vier mögliche Fälle auftreten:

Richtig positiv: Der Patient ist krank, und der Test hat dies richtig angezeigt.
Falsch negativ: Der Patient ist krank, aber der Test hat ihn fälschlicherweise als gesund eingestuft.
Falsch positiv: Der Patient ist gesund, aber der Test hat ihn fälschlicherweise als krank eingestuft.
Richtig negativ: Der Patient ist gesund, und der Test hat dies richtig angezeigt.

Im ersten und letzten Fall war die Diagnose also richtig, in den anderen beiden Fällen liegt ein Fehler vor. Die vier Fälle werden in verschiedenen Kontexten auch anders benannt. So sind auch die englischen Begriffe true positive, false positive, false negative und true negative gebräuchlich. Im Rahmen der Signalentdeckungstheorie werden richtig positive Fälle auch als hit, falsch negative Fälle als miss und richtig negative Fälle als correct rejection bezeichnet.

Es wird nun gezählt, wie häufig jede der vier möglichen Kombinationen von Testergebnis (ermittelte Klasse) und Gesundheitszustand (tatsächliche Klasse) vorgekommen ist. Diese Häufigkeiten werden in eine sogenannte Wahrheitsmatrix (auch Konfusionsmatrix genannt) eingetragen:

Wahrheitsmatrix (Konfusionsmatrix)
	Person ist krank ( $r_{\text{p}}+f_{\text{n}}$ )	Person ist gesund ( $f_{\text{p}}+r_{\text{n}}$ )
Test positiv ( $r_{\text{p}}+f_{\text{p}}$ )	richtig positiv ( $r_{\text{p}}$ )	falsch positiv ( $f_{\text{p}}$ )	∑: 100 % der positiven Tests
Test negativ ( $f_{\text{n}}+r_{\text{n}}$ )	falsch negativ ( $f_{\text{n}}$ )	richtig negativ ( $r_{\text{n}}$ )	∑: 100 % der negativen Tests
	∑: 100 % der kranken Personen	∑: 100 % der gesunden Personen

Anmerkungen: $f$ steht für „falsch“ (genauer: für die Anzahl an falschen Einstufungen); $r$ steht für „richtig“ (genauer: für die Anzahl an richtigen Einstufungen); der Index ${\text{p}}$ steht für „positiv“; der Index ${\text{n}}$ steht für „negativ“. Also: $r_{\text{p}}$ steht für „richtig positiv“ (genauer: für die Anzahl an richtigerweise als positiv Eingestuften) usw.

Diese Matrix ist ein einfacher Spezialfall einer Kontingenztafel mit zwei binären nominalen Variablen – dem Urteil des Klassifikators und der tatsächlichen Klasse. Sie kann auch für Klassifikationen mit mehr als zwei Klassen eingesetzt werden, dann wird bei $N$ Klassen aus einer 2×2-Matrix eine $N\times N$ -Matrix.

Statistische Gütekriterien der Klassifikation

Durch Berechnung verschiedener relativer Häufigkeiten können aus den Werten der Wahrheitsmatrix nun Kenngrößen zur Beurteilung des Klassifikators berechnet werden. Diese können auch als Schätzungen der bedingten Wahrscheinlichkeit für das Eintreten des entsprechenden Ereignisses interpretiert werden. Die Maße unterscheiden sich hinsichtlich der Grundgesamtheit, auf die sich die relativen Häufigkeiten beziehen: So können etwa nur all die Fälle in Betracht gezogen werden, in denen die positive bzw. negative Kategorie tatsächlich vorliegt, oder man betrachtet die Menge aller Objekte, die als positiv bzw. negativ klassifiziert werden (Summe über die Einträge einer Zeile der Wahrheitsmatrix). Diese Wahl hat gravierende Auswirkungen auf die berechneten Werte, insbesondere dann, wenn eine der beiden Klassen insgesamt viel häufiger vorkommt als die andere.

Sensitivität

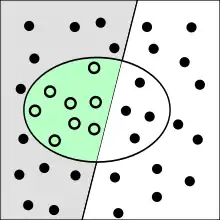
Der Bereich mit Kreisen anstelle von Punkten repräsentiert die Sensitivität eines Tests. Links vom schwarzen Strich sind die kranken, rechts die gesunden Menschen abgebildet. Die Punkte im Oval repräsentieren die vom Test als krank eingestuften Personen.

Die Sensitivität (auch Richtig-positiv-Rate, Empfindlichkeit oder Trefferquote; englisch sensitivity, true positive rate, recall oder hit rate) gibt die Wahrscheinlichkeit an, mit der ein positives Objekt korrekt als positiv klassifiziert wird. Beispielsweise entspricht die Sensitivität bei einer medizinischen Diagnose dem Anteil an tatsächlich Kranken, bei denen die Krankheit auch erkannt wurde. Die Sensitivität eines Tests gibt an, mit welcher Wahrscheinlichkeit ein Infizierter auch tatsächlich erkannt wurde. Beispielsweise bedeutet eine Sensitivität eines Tests auf ein Virus von 98 %, dass (bei ausreichend großer Anzahl an durchgeführten Tests und unabhängig von den Testvorbedingungen) 98 % der Infizierten erkannt und 2 % der Infizierten nicht erkannt würden. 2 % (der Infizierten, welche getestet wurden, und nicht aller Getesteten) wären dann also falsch negativ.

Die Sensitivität entspricht der geschätzten bedingten Wahrscheinlichkeit

P({\text{positives Testergebnis}}|{\text{tatsächlich krank}})={\frac {r_{\text{p}}}{r_{\text{p}}+f_{\text{n}}}}

.

Im Kontext des statistischen Hypothesentests wird die Sensitivität des Tests als Trennschärfe des Tests bezeichnet, obwohl der Begriff Trennschärfe in diesem Kontext eine allgemeinere Verwendung hat, die im vorliegenden Kontext nicht anwendbar ist.

Falsch-negativ-Rate

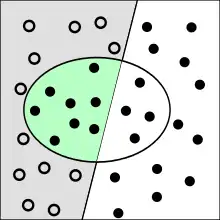
Der Bereich mit Kreisen anstelle von Punkten repräsentiert die Falsch-negativ-Rate eines Tests. Links vom schwarzen Strich sind die kranken, rechts die gesunden Menschen abgebildet. Die Punkte im Oval repräsentieren die vom Test als krank eingestuften Personen.

Entsprechend gibt die Falsch-negativ-Rate (englisch false negative rate oder miss rate) den Anteil der fälschlich als negativ klassifizierten Objekte an der Gesamtheit der positiven Objekte an. Also im Beispiel die tatsächlich Kranken, die aber als gesund diagnostiziert werden.

Die Falsch-negativ-Rate entspricht der geschätzten bedingten Wahrscheinlichkeit

P({\text{negatives Testergebnis}}|{\text{tatsaechlich krank}})={\frac {f_{\text{n}}}{r_{\text{p}}+f_{\text{n}}}}

.

Zusammenhang

Da sich beide Maße auf den Fall beziehen, dass in Wirklichkeit die positive Kategorie vorliegt (erste Spalte der Wahrheitsmatrix), addieren sich die Sensitivität und die Falsch-negativ-Rate zu 1 bzw. 100 %.

{\text{Sensitivitaet}}+{\text{Falsch-negativ-Rate}}=1

Spezifität

Der Bereich mit Kreisen anstelle von Punkten repräsentiert die Spezifität eines Tests. Links vom schwarzen Strich sind die kranken, rechts die gesunden Menschen abgebildet. Die Punkte im Oval repräsentieren die vom Test als krank eingestuften Personen.

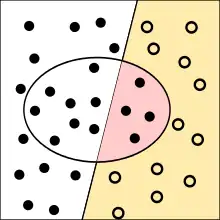
Die Spezifität (auch Richtig-negativ-Rate oder kennzeichnende Eigenschaft; englisch: specificity, true negative rate oder correct rejection rate) gibt die Wahrscheinlichkeit an, mit der ein negatives Objekt korrekt als negativ klassifiziert wird. Beispielsweise entspricht die Spezifität bei einer medizinischen Diagnose den Anteil an Gesunden, bei denen auch festgestellt wurde, dass keine Krankheit vorliegt. Die Spezifität eines Tests gibt an, mit welcher Wahrscheinlichkeit ein Nicht-Infizierter auch tatsächlich erkannt würde. Beispielsweise bedeutet eine Spezifität eines Tests auf ein Virus von 98 %, dass (bei ausreichend großer Anzahl an durchgeführten Tests und unabhängig von den Testvorbedingungen) 98 % der Nicht-Infizierten tatsächlich erkannt und 2 % der Nicht-Infizierten fälschlich als infiziert ausgewiesen würden. 2 % (der getesteten Nicht-Infizierten, nicht der Getesteten insgesamt) wären dann also falsch positiv.

Die Spezifität entspricht der geschätzten bedingten Wahrscheinlichkeit

P({\text{negatives Testergebnis}}|{\text{tatsaechlich gesund}})={\frac {r_{\text{n}}}{r_{\text{n}}+f_{\text{p}}}}

.

Falsch-positiv-Rate

Der Bereich mit Kreisen anstelle von Punkten repräsentiert die Falsch-positiv-Rate eines Tests. Links vom schwarzen Strich sind die kranken, rechts die gesunden Menschen abgebildet. Die Punkte im Oval repräsentieren die vom Test als krank eingestuften Personen.

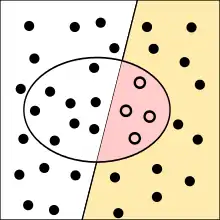
Entsprechend gibt die Falsch-positiv-Rate (auch Ausfallrate; englisch fallout oder false positive rate) den Anteil der fälschlich als positiv klassifizierten Objekte an, die in Wirklichkeit negativ sind. Im Beispiel würde dann ein tatsächlich Gesunder zu Unrecht als krank diagnostiziert. Es wird also die Wahrscheinlichkeit für einen Fehlalarm angegeben.

Die Falsch-positiv-Rate entspricht der geschätzten bedingten Wahrscheinlichkeit

P({\text{positives Testergebnis}}|{\text{tatsaechlich gesund}})={\frac {f_{\text{p}}}{r_{\text{n}}+f_{\text{p}}}}

.

Zusammenhang

Da sich beide Maße auf den Fall beziehen, dass in Wirklichkeit die negative Kategorie vorliegt (zweite Spalte der Wahrheitsmatrix), addieren sich die Spezifität und die Falsch-positiv-Rate zu 1 bzw. 100 %.

{\text{Spezifitaet}}+{\text{Falsch-positiv-Rate}}=1

Positiver und negativer Vorhersagewert

Während Sensitivität und Spezifität eines medizinischen Tests epidemiologisch und gesundheitspolitisch relevante Kenngrößen sind (beispielsweise bei der Frage, ob ein Einsatz im Screening zur Früherkennung von Krankheiten sinnvoll ist), ist im konkreten Fall für Patient und Arzt der Vorhersagewert entscheidend. Nur er beantwortet einem positiv/negativ Getesteten die Frage, mit welcher Wahrscheinlichkeit er denn nun wirklich krank/gesund ist.

Positiver Vorhersagewert

Positiver Vorhersagewert

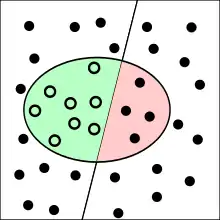
Der positive Vorhersagewert (auch Relevanz, Wirksamkeit, Genauigkeit, positiver prädiktiver Wert; englisch: precision oder positive predictive value; Abkürzung: PPV) gibt den Anteil der korrekt als positiv klassifizierten Ergebnisse an der Gesamtheit der als positiv klassifizierten Ergebnisse an (erste Zeile der Wahrheitsmatrix). Beispielsweise gibt der positive Vorhersagewert eines medizinischen Tests an, welcher Anteil der Personen mit positivem Testergebnis auch tatsächlich krank ist.

Der positive Vorhersagewert entspricht der geschätzten bedingten Wahrscheinlichkeit

P({\text{tatsaechlich krank}}|{\text{positives Testergebnis}})={\frac {r_{\text{p}}}{r_{\text{p}}+f_{\text{p}}}}

.

Komplement des positiven Vorhersagewerts ist die als bedingte Wahrscheinlichkeit wie folgt zu formulierende Falscherkennungsrate (englisch: false discovery rate; Abkürzung: FDR):

P({\text{tatsaechlich gesund}}|{\text{positives Testergebnis}})={\frac {f_{\text{p}}}{r_{\text{p}}+f_{\text{p}}}}

.

Negativer Vorhersagewert

Negativer Vorhersagewert

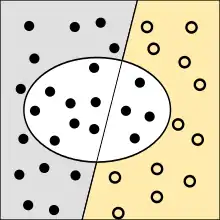
Entsprechend gibt der negative Vorhersagewert (auch Segreganz oder Trennfähigkeit; englisch: negative predictive value; Abkürzung: NPV) den Anteil der korrekt als negativ klassifizierten Ergebnisse an der Gesamtheit der als negativ klassifizierten Ergebnisse an (zweite Zeile der Wahrheitsmatrix). Im Beispiel entspricht das dem Anteil der Personen mit negativem Testergebnis, der auch tatsächlich gesund ist.

Der negative Vorhersagewert entspricht der geschätzten bedingten Wahrscheinlichkeit

P({\text{tatsaechlich gesund}}|{\text{negatives Testergebnis}})={\frac {r_{\text{n}}}{r_{\text{n}}+f_{\text{n}}}}.

Komplement des negativen Vorhersagewerts ist die als bedingte Wahrscheinlichkeit wie folgt zu formulierende Falschauslassungsrate (englisch: false omission rate; Abkürzung: FOR):

P({\text{tatsaechlich krank}}|{\text{negatives Testergebnis}})={\frac {f_{\text{n}}}{r_{\text{n}}+f_{\text{n}}}}

.

Zusammenhänge

Anders als die anderen Paare von Gütemaßen addieren sich der negative und der positive Vorhersagewert nicht zu 1 bzw. 100 %, da jeweils von unterschiedlichen Fällen ausgegangen wird (tatsächlich positiv bzw. tatsächlich negativ, d. h. unterschiedliche Spalten der Wahrheitsmatrix). Die Vorhersagewerte können aus Sensitivität $s$ und Spezifität $z$ berechnet werden, dazu muss aber die Prätestwahrscheinlichkeit $p$ (entspricht bei Krankheiten der Prävalenz in der untersuchten Population) bekannt sein oder geschätzt werden. Der positive Vorhersagewert profitiert von einer hohen Prätestwahrscheinlichkeit, der negative Vorhersagewert von einer niedrigen Prätestwahrscheinlichkeit. Ein positives medizinisches Testergebnis hat also eine viel höhere Aussagekraft, wenn der Test auf Verdacht durchgeführt wurde, als wenn er allein dem Screening diente.

Vierfeldertafel mit relativen Häufigkeiten und Berechnung der Vorhersagewerte
	krank	gesund	Summe	Vorhersagewert
positiv	$s\cdot p$	$(1-z)\cdot (1-p)$	$s\cdot p+(1-z)\cdot (1-p)$	${\frac {s\cdot p}{s\cdot p+(1-z)\cdot (1-p)}}$
negativ	$(1-s)\cdot p$	$z\cdot (1-p)$	$(1-s)\cdot p+z\cdot (1-p)$	${\frac {z\cdot (1-p)}{(1-s)\cdot p+z\cdot (1-p)}}$
Summe	$p$	$1-p$	$1$

Die für ein Kollektiv ermittelten positiven und negativen Vorhersagewerte sind auf andere Kollektive nur dann übertragbar, wenn die relative Häufigkeit der positiven Fälle dort dieselbe ist. Beispiel: Wurden zur Bestimmung des positiven Vorhersagewerts 100 HIV-Patienten und 100 gesunde Kontrollpatienten untersucht, so ist der Anteil an HIV-Patienten in dieser Gruppe (50 %) weit von der HIV-Prävalenz in der BRD (0,08 %) entfernt (siehe dazu auch das unten genannte Zahlenbeispiel). Die Vorhersagewerte wären also völlig andere, wenn derselbe Test an einem zufällig ausgewählten Menschen durchgeführt wird.

Likelihood-Quotienten

Einfacher als die Wahrscheinlichkeit des Vorliegens einer Krankheit lässt sich die Chance (Odd) des Vorliegens einer Krankheit berechnen. Ein positives Testergebnis vergrößert die Chance, krank zu sein, um einen Faktor (Odds-Ratio), der als Likelihood-Quotient (LQ) oder Bayes-Faktor bezeichnet und folgendermaßen berechnet wird:[1]

\mathrm {LQ} _{\text{positiv}}={\frac {\text{Sensitivität}}{1-{\text{Spezifität}}}}

Die Chance $o({\text{krank}}|{\text{positiv}})$ , bei positivem Testergebnis tatsächlich krank zu sein, beträgt somit

o({\text{krank}}|{\text{positiv}})=o_{\text{vor dem Test}}\cdot {\frac {\text{Sensitivität}}{1-{\text{Spezifität}}}}

.

Da kleine Chancen näherungsweise mit Wahrscheinlichkeiten gleichgesetzt werden können, lässt sich der positive Vorhersagewert oft über das Produkt von Prätestwahrscheinlichkeit und Bayes-Faktor abschätzen.

Ein negatives Testergebnis verändert die Chance analog um den Bayes-Faktor

\mathrm {LQ} _{\text{negativ}}={\frac {1-{\text{Sensitivität}}}{\text{Spezifität}}}

.

Ein weiteres sich aus den beiden obengenannten Kenngrößen ableitendes und damit ebenfalls prävalenzunabhängiges Maß der Leistungsfähigkeit eines Tests ist das sogen. Diagnostische Chancenverhältnis (DOR) (engl. diagnostic odds ratio), das sich wie folgt berechnet:

\mathrm {DOR} ={\frac {\mathrm {LQ} _{\text{positiv}}}{\mathrm {LQ} _{\text{negativ}}}}={\frac {{\text{Sensitivitaet}}\cdot {\text{Spezifitaet}}}{(1-{\text{Sensitivitaet}})\cdot (1-{\text{Spezifitaet}})}}

.

Korrekt- und Falschklassifikationsrate

Die Korrektklassifikationsrate (auch Vertrauenswahrscheinlichkeit oder Treffergenauigkeit; englisch: accuracy) gibt den Anteil aller Objekte an, die korrekt klassifiziert werden. Der restliche Anteil entspricht der Falschklassifikationsrate (auch Größe des Klassifikationsfehlers). Im Beispiel der Diagnose wäre die Korrektklassifikationsrate der Anteil an richtig positiven und richtig negativen Diagnosen an der Gesamtzahl der Diagnosen, die Falschklassifikationsrate hingegen der Anteil der falsch positiven und falsch negativen Diagnosen.

Korrektklassifikationsrate

Korrektklassifikationsrate

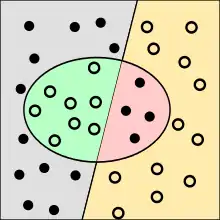
Die Korrektklassifikationsrate entspricht der geschätzten Wahrscheinlichkeit

P({\text{richtig klassifiziert}})={\frac {\text{richtig klassifiziert}}{\text{alle Faelle}}}={\frac {r_{\text{p}}+r_{\text{n}}}{r_{\text{p}}+f_{\text{p}}+r_{\text{n}}+f_{\text{n}}}}

.

Falschklassifikationsrate

Falschklassifikationsrate

Die Falschklassifikationsrate entspricht der geschätzten Wahrscheinlichkeit

P({\text{falsch klassifiziert}})={\frac {\text{falsch klassifiziert}}{\text{alle Faelle}}}={\frac {f_{\text{p}}+f_{\text{n}}}{r_{\text{p}}+f_{\text{p}}+r_{\text{n}}+f_{\text{n}}}}

.

Zusammenhang

Die Korrekt- und die Falschklassifikationsrate addieren sich entsprechend zu 1 oder 100 %.

{\text{Korrektklassifikationsrate}}+{\text{Falschklassifikationsrate}}=1

Kombinierte Maße

Da sich die verschiedenen Gütemaße gegenseitig beeinflussen (siehe Abschnitt Probleme), wurden verschiedene kombinierte Maße vorgeschlagen, die eine Beurteilung der Güte mit einer einzigen Kennzahl erlauben. Die im Folgenden vorgestellten Maße wurden im Kontext des Information Retrieval entwickelt (siehe Anwendung im Information Retrieval).

F-Maß

Das F-Maß kombiniert Genauigkeit (precision, $P$ ) und Trefferquote (recall, $R$ ) mittels des gewichteten harmonischen Mittels:

F=2\cdot {\frac {P\cdot R}{P+R}}

Neben diesem auch als $F_{1}$ bezeichneten Maß, bei dem Genauigkeit und Trefferquote gleich gewichtet sind, gibt es auch andere Gewichtungen. Der Allgemeinfall ist das Maß $F_{\alpha }$ (für positive Werte von $\alpha$ ):

F_{\alpha }=(1+\alpha ^{2})\cdot {\frac {P\cdot R}{\alpha ^{2}\cdot P+R}}

Beispielsweise gewichtet $F_{2}$ die Trefferquote viermal so hoch wie die Genauigkeit und $F_{0{,}5}$ die Genauigkeit viermal so hoch wie die Trefferquote.

Effektivitätsmaß

Das Effektivitätsmaß $E$ entspricht ebenfalls dem gewichteten harmonischen Mittel. Es wurde 1979 von Cornelis Joost van Rijsbergen eingeführt. Die Effektivität liegt zwischen 0 (beste Effektivität) und 1 (schlechte Effektivität). Für einen Parameterwert von $\alpha =0$ ist $E$ äquivalent zur Trefferquote, für einen Parameterwert von $\alpha =1$ äquivalent zur Genauigkeit.

E=1-{\frac {1}{\alpha \left({\frac {1}{P}}\right)+(1-\alpha ){\frac {1}{R}}}}

Funktionsgraphen

Funktionsgraphen von

{\color [rgb]{1,0,0}f_{1}(x)={\tfrac {x}{x+1}}}

und

{\color [rgb]{0,0,1}f_{2}(x)={\tfrac {1}{x+1}}}

Für die sechs Kennzahlen Sensitivität, Falsch-negativ-Rate, Spezifität, Falsch-positiv-Rate, positiver Vorhersagewert und negativer Vorhersagewert lassen sich normierte, zweidimensionale Funktionsgraphen darstellen:

Betrachtet man beispielsweise das Verhältnis von $r_{\text{p}}$ zu $f_{\text{n}}$ und setzt

x_{\text{pn}}:={\frac {r_{\text{p}}}{f_{\text{n}}}}

,

so erhält man für die Sensitivität

{\text{Sensitivitaet}}={\frac {r_{\text{p}}}{r_{\text{p}}+f_{\text{n}}}}={\frac {x_{\text{pn}}\cdot f_{\text{n}}}{x_{\text{pn}}\cdot f_{\text{n}}+f_{\text{n}}}}={\frac {x_{\text{pn}}}{x_{\text{pn}}+1}}={\color [rgb]{1,0,0}f_{1}(x_{\text{pn}})}={\color [rgb]{0,0,1}f_{2}\left({\frac {1}{x_{\text{pn}}}}\right)}

und für die Falsch-negativ-Rate

{\text{Falsch-negativ-Rate}}={\frac {f_{\text{n}}}{r_{\text{p}}+f_{\text{n}}}}={\frac {f_{\text{n}}}{x_{\text{pn}}\cdot f_{\text{n}}+f_{\text{n}}}}={\frac {1}{x_{\text{pn}}+1}}={\color [rgb]{0,0,1}f_{2}(x_{\text{pn}})}={\color [rgb]{1,0,0}f_{1}\left({\frac {1}{x_{\text{pn}}}}\right)}

,

wobei die beiden Funktionen ${\color [rgb]{1,0,0}f_{1}(x)}$ und ${\color [rgb]{0,0,1}f_{2}(x)}$ , deren Graphen hier abgebildet sind, definiert sind als:

${\color [rgb]{1,0,0}f_{1}(x):={\frac {x}{x+1}}}$
${\color [rgb]{0,0,1}f_{2}(x):={\frac {1}{x+1}}}$

Diese Vorgangsweise ist nur deshalb möglich, weil die Sensitivität die Eigenschaft besitzt, dass es für ihren Wert nicht auf die beiden konkreten Einzelwerte $r_{\text{p}}$ und $f_{\text{n}}$ ankommt, sondern ausschließlich auf deren Verhältnis ${\tfrac {r_{\text{p}}}{f_{\text{n}}}}$ (bzw. dessen Kehrwert ${\tfrac {f_{\text{n}}}{r_{\text{p}}}}$ ). Daher kann die Sensitivität, die – als zweistellige Funktion formuliert – von den zwei Variablen $r_{\text{p}}$ und $f_{\text{n}}$ abhängt, auch als einstellige Funktion in Abhängigkeit von $x_{\text{pn}}:={\tfrac {r_{\text{p}}}{f_{\text{n}}}}$ (bzw. ${\tilde {x}}_{\text{pn}}:={\tfrac {f_{\text{n}}}{r_{\text{p}}}}$ ) dargestellt werden, wodurch sich zweidimensionale Funktionsgraphen zeichnen lassen. Dasselbe gilt auch für die Falsch-negativ-Rate.

Für die übrigen vier Kennwerte lässt sich analog vorgehen (wobei zu beachten ist, dass für $x$ verschiedene Verhältnisse verwendet werden), wie die folgende tabellarische Zusammenfassung zeigt:

Zusammenfassung
Kennzahl	Verhältnis	Formel
Sensitivität	$x_{\text{pn}}:={\frac {r_{\text{p}}}{f_{\text{n}}}}$	${\frac {r_{\text{p}}}{r_{\text{p}}+f_{\text{n}}}}={\frac {x_{\text{pn}}}{x_{\text{pn}}+1}}={\color [rgb]{1,0,0}f_{1}(x_{\text{pn}})}={\color [rgb]{0,0,1}f_{2}\left({\frac {1}{x_{\text{pn}}}}\right)}$
Falsch-negativ-Rate	$x_{\text{pn}}:={\frac {r_{\text{p}}}{f_{\text{n}}}}$	${\frac {f_{\text{n}}}{r_{\text{p}}+f_{\text{n}}}}={\frac {1}{x_{\text{pn}}+1}}={\color [rgb]{0,0,1}f_{2}(x_{\text{pn}})}={\color [rgb]{1,0,0}f_{1}\left({\frac {1}{x_{\text{pn}}}}\right)}$
Spezifität	$x_{\text{np}}:={\frac {r_{\text{n}}}{f_{\text{p}}}}$	${\frac {r_{\text{n}}}{r_{\text{n}}+f_{\text{p}}}}={\frac {x_{\text{np}}}{x_{\text{np}}+1}}={\color [rgb]{1,0,0}f_{1}(x_{\text{np}})}={\color [rgb]{0,0,1}f_{2}\left({\frac {1}{x_{\text{np}}}}\right)}$
Falsch-positiv-Rate	$x_{\text{np}}:={\frac {r_{\text{n}}}{f_{\text{p}}}}$	${\frac {f_{\text{p}}}{r_{\text{n}}+f_{\text{p}}}}={\frac {1}{x_{\text{np}}+1}}={\color [rgb]{0,0,1}f_{2}(x_{\text{np}})}={\color [rgb]{1,0,0}f_{1}\left({\frac {1}{x_{\text{np}}}}\right)}$
Positiver Vorhersagewert	$x_{\text{pp}}:={\frac {r_{\text{p}}}{f_{\text{p}}}}$	${\frac {r_{\text{p}}}{r_{\text{p}}+f_{\text{p}}}}={\frac {x_{\text{pp}}}{x_{\text{pp}}+1}}={\color [rgb]{1,0,0}f_{1}(x_{\text{pp}})}={\color [rgb]{0,0,1}f_{2}\left({\frac {1}{x_{\text{pp}}}}\right)}$
Negativer Vorhersagewert	$x_{\text{nn}}:={\frac {r_{\text{n}}}{f_{\text{n}}}}$	${\frac {r_{\text{n}}}{r_{\text{n}}+f_{\text{n}}}}={\frac {x_{\text{nn}}}{x_{\text{nn}}+1}}={\color [rgb]{1,0,0}f_{1}(x_{\text{nn}})}={\color [rgb]{0,0,1}f_{2}\left({\frac {1}{x_{\text{nn}}}}\right)}$

Probleme

Gegenseitige Beeinflussungen

Es ist nicht möglich, alle Gütekriterien unabhängig voneinander zu optimieren. Insbesondere sind die Sensitivität und die Spezifität negativ miteinander korreliert. Zur Veranschaulichung dieser Zusammenhänge ist es hilfreich, die Extremfälle zu betrachten:

Wenn eine Diagnose fast alle Patienten als krank klassifiziert (liberale Diagnose), ist die Sensitivität maximal, denn es werden die meisten Kranken auch als solche erkannt. Allerdings wird gleichzeitig auch die Falsch-positiv-Rate maximal, da auch fast alle Gesunden als krank eingestuft werden. Die Diagnose hat also eine sehr geringe Spezifität.
Wird hingegen fast niemand als krank eingestuft (konservative Diagnose), ist umgekehrt die Spezifität maximal, allerdings auf Kosten einer geringen Sensitivität.

Wie konservativ oder liberal ein Klassifikator optimalerweise sein sollte, hängt vom konkreten Anwendungsfall ab. Aus diesem leitet sich beispielsweise ab, welche der Fehlklassifikationen die schwererwiegenden Folgen hat. Bei der Diagnose einer schlimmen Krankheit oder sicherheitsrelevanten Anwendungen wie einem Feueralarm ist es wichtig, dass kein Fall unentdeckt bleibt. Bei einer Recherche durch eine Suchmaschine hingegen kann es wichtiger sein, möglichst wenige Resultate zu bekommen, die für die Suche irrelevant sind, also falsch-positive Resultate darstellen. Die Risiken der verschiedenen Fehlklassifikationen lassen sich zur Bewertung eines Klassifikators in einer Kostenmatrix angeben, mit der die Wahrheitsmatrix gewichtet wird. Eine weitere Möglichkeit besteht in der Verwendung kombinierter Maße, bei denen sich eine entsprechende Gewichtung einstellen lässt.

Um die Auswirkungen verschieden konservativer Tests für ein konkretes Anwendungsbeispiel darzustellen, können ROC-Kurven erstellt werden, in denen die Sensitivität für verschiedene Tests gegen die Falsch-positiv-Rate aufgetragen wird. Im Rahmen der Signalentdeckungstheorie spricht man auch von einem verschieden konservativ gesetzten Kriterium.

Seltene Positiv-Fälle

Darüber hinaus wird auch ein extremes Ungleichgewicht zwischen tatsächlich positiven und negativen Fällen die Kenngrößen verfälschen, wie es etwa bei seltenen Krankheiten der Fall ist. Ist beispielsweise die Anzahl der an einem Test teilnehmenden Kranken erheblich geringer als die der Gesunden, so führt dies im Allgemeinen zu einem geringen Wert im positiven Vorhersagewert (siehe dazu das unten angeführte Zahlenbeispiel). Daher sollte in diesem Fall alternativ zu den Vorhersagewerten der Likelihood-Quotient angegeben werden.

Dieser Zusammenhang ist bei verschiedenen Labortests zu bedenken: Preiswerte Screening-Tests werden so justiert, dass eine möglichst kleine Anzahl falsch negativer Ergebnisse vorliegt. Die produzierten falsch positiven Testergebnisse werden anschließend durch einen (teureren) Bestätigungstest identifiziert. Für schwerwiegende Erkrankungen sollte immer ein Bestätigungstest durchgeführt werden. Dieses Vorgehen ist für die Bestimmung von HIV sogar gefordert.

Unvollständige Wahrheitsmatrix

Ein weiteres Problem bei der Beurteilung eines Klassifikators besteht darin, dass häufig nicht die gesamte Wahrheitsmatrix ausgefüllt werden kann. Insbesondere ist oft die Falsch-negativ-Rate nicht bekannt, etwa wenn bei Patienten, die eine negative Diagnose erhalten, keine weiteren Tests durchgeführt werden und eine Krankheit unerkannt bleibt, oder wenn ein eigentlich relevantes Dokument bei einer Recherche nicht gefunden wird, weil es nicht als relevant klassifiziert wurde. In diesem Fall können nur die als positiv klassifizierten Ergebnisse ausgewertet werden, d. h., es kann nur der positive Vorhersagewert berechnet werden (siehe dazu auch das unten angeführte Zahlenbeispiel). Mögliche Lösungen für dieses Problem werden im Abschnitt Anwendung im Information Retrieval besprochen.

Klassifikationsbewertung und statistische Testtheorie

	Binäre Klassifikation	Statistischer Test
Ziel	Auf Basis einer Stichprobe werden Beobachtungen (Objekte) einer der beiden Klassen zugeordnet.	Mittels einer Zufallsstichprobe werden zwei sich ausschließende Hypothesen (Null- und Alternativhypothese) über die Grundgesamtheit geprüft.
Vorgehen	Der Klassifikator ist eine aus der Stichprobe geschätzte Regressionsfunktion mit zwei möglichen Ergebniswerten.	Der Prüfwert wird mittels einer Teststatistik aus der Zufallsstichprobe berechnet und mit kritischen Werten, die aus der Verteilung der Teststatistik berechnet werden, verglichen.
Ergebnis	Für eine Beobachtung wird eine Klassenzugehörigkeit vorhergesagt.	Aufgrund des Vergleiches von Prüfwert und kritischen Werten kann die Alternativhypothese angenommen oder verworfen werden.
Fehler	Die Qualität eines Klassifikators wird mit der Falschklassifikationsrate (falsch positiv und falsch negativ) im Nachhinein beurteilt.	Vor der Testdurchführung wird die Größe des Fehlers 1. Art (fälschlich Annahme der Alternativhypothese) festgelegt. Daraus werden die kritischen Werte berechnet. Der Fehler 2. Art (fälschlich Ablehnung der Alternativhypothese) ist immer unbekannt bei der Testdurchführung.

Klassifikationsbewertung zur Beurteilung der Qualität statistischer Tests

Mit Hilfe der Klassifikationsbewertung kann die Qualität eines statistischen Tests beurteilt werden:

Generiert man viele Stichproben unter Gültigkeit der Nullhypothese, so sollte die Annahmerate der Alternativhypothese dem Fehler 1. Art entsprechen. Aber bei komplizierten Tests kann man oft nur eine obere Grenze für den Fehler 1. Art angeben, sodass der „wahre“ Fehler 1. Art nur mit einer solchen Simulation abgeschätzt werden kann.
Generiert man viele Stichproben unter Gültigkeit der Alternativhypothese, so ist die Ablehnungsrate der Alternativhypothese eine Schätzung des Fehlers 2. Art. Dies ist beispielsweise von Interesse, wenn man zwei Tests für einen Sachverhalt hat. Wenn die Alternativhypothese gilt, dann bevorzugt man den Test, der einen kleineren Fehler 2. Art hat.

Statistische Tests zur Beurteilung einer Klassifikation

Man kann statistische Tests einsetzen, um zu überprüfen, ob eine Klassifikation statistisch signifikant ist, d. h., ob bezüglich der Grundgesamtheit die Einschätzung des Klassifikators unabhängig von den tatsächlichen Klassen ist (Nullhypothese) oder ob er signifikant mit ihnen korreliert (Alternativhypothese).

Im Fall von mehreren Klassen kann dafür der Chi-Quadrat-Unabhängigkeitstest verwendet werden. Dabei wird geprüft, ob die Einschätzung des Klassifikators unabhängig von den tatsächlichen Klassen ist oder signifikant mit ihnen korreliert. Die Stärke der Korrelation wird durch Kontingenzkoeffizienten abgeschätzt.

Im Fall einer binären Klassifikation wird der Vierfeldertest verwendet, ein Spezialfall des Chi-Quadrat-Unabhängigkeitstests. Hat man nur wenige Beobachtungswerte, sollte der Exakte Fisher-Test verwendet werden. Die Stärke der Korrelation kann mit dem Phi-Koeffizient abgeschätzt werden.

Lehnt der Test die Nullhypothese ab, bedeutet es jedoch nicht, dass der Klassifikator gut ist. Es bedeutet nur, dass er besser ist als (zufälliges) Raten. Ein guter Klassifikator sollte auch eine möglichst hohe Korrelation aufweisen.

In Diettrich (1998) werden fünf Tests untersucht zum direkten Vergleich von Missklassifikationsraten von zwei unterschiedlichen Klassifikatoren:[2]

Ein einfacher Zweistichproben-t-Test für unabhängige Stichproben,
ein Zweistichproben-t-Test für verbundene Stichproben,
ein Zweistichproben-t-Test für verbundene Stichproben mit 10-fach-Kreuzvalidierung,
der McNemar-Test und
ein Zweistichproben-t-Test für verbundene Stichproben mit 5-fach-Kreuzvalidierung und modifizierter Varianzberechnung (5x2cv).

Als Ergebnis der Untersuchung von Güte und Fehler 1. Art der fünf Tests ergibt sich, dass sich der 5x2cv-Test am besten verhält, jedoch sehr rechenaufwendig ist. Der McNemar-Test ist etwas schlechter als der 5x2cv-Test, jedoch deutlich weniger rechenaufwendig.

Anwendung im Information Retrieval

Ein spezieller Anwendungsfall der hier beschriebenen Maße ist die Beurteilung der Güte von Treffermengen einer Recherche beim Information Retrieval. Dabei geht es um die Beurteilung, ob ein gefundenes Dokument, etwa beim Webmining durch Suchmaschinen, entsprechend einem definierten Kriterium relevant ist. In diesem Zusammenhang sind die oben definierten Bezeichnungen „Trefferquote“ (engl. recall), „Genauigkeit“ (engl. precision) und „Ausfallquote“ (engl. fallout) gebräuchlich. Die Trefferquote gibt den Anteil der bei einer Suche gefundenen relevanten Dokumente und damit die Vollständigkeit eines Suchergebnisses an. Die Genauigkeit beschreibt mit dem Anteil relevanter Dokumente an der Ergebnismenge die Genauigkeit eines Suchergebnisses. Der (weniger gebräuchliche) Ausfall bezeichnet den Anteil gefundener irrelevanter Dokumente an der Gesamtmenge aller irrelevanten Dokumente, er gibt also in negativer Weise an, wie gut irrelevante Dokumente im Suchergebnis vermieden werden. Statt als Maß können Trefferquote, Genauigkeit und Ausfall auch als Wahrscheinlichkeit interpretiert werden:

Trefferquote ist die Wahrscheinlichkeit, mit der ein relevantes Dokument gefunden wird (Sensitivität).
Genauigkeit ist die Wahrscheinlichkeit, mit der ein gefundenes Dokument relevant ist (Positiver Vorhersagewert).
Ausfall ist die Wahrscheinlichkeit, mit der ein irrelevantes Dokument gefunden wird (Falsch-positiv-Rate).

Eine gute Recherche sollte möglichst alle relevanten Dokumente finden (richtig positiv) und die nicht relevanten Dokumente nicht finden (richtig negativ). Wie oben beschrieben, hängen die verschiedenen Maße jedoch voneinander ab. Im Allgemeinen sinkt mit steigender Trefferrate die Genauigkeit (mehr irrelevante Ergebnisse). Umgekehrt sinkt mit steigender Genauigkeit (weniger irrelevante Ergebnisse) die Trefferrate (mehr relevante Dokumente, die nicht gefunden werden). Je nach Anwendungsfall sind die unterschiedlichen Maße zur Beurteilung mehr oder weniger relevant. Bei einer Patentrecherche ist es beispielsweise wichtig, dass keine relevanten Patente unentdeckt bleiben – also sollte der Negative Vorhersagewert möglichst hoch sein. Bei anderen Recherchen ist es wichtiger, dass die Treffermenge wenige irrelevante Dokumente enthält, d. h., der Positive Vorhersagewert sollte möglichst hoch sein.

Im Kontext des Information Retrieval wurden auch die oben beschriebenen kombinierten Maße wie der F-Wert und die Effektivität eingeführt.

Genauigkeit-Trefferquote-Diagramm

Zur Einschätzung eines Retrieval-Verfahrens werden meist Trefferquote und Genauigkeit gemeinsam betrachtet. Dazu werden im sogenannten Precision-Recall-Diagramm (PR-Diagramm) für verschieden große Treffermengen zwischen den beiden Extremen Genauigkeit auf der $y$ -Achse und Trefferquote auf der $x$ -Achse eingetragen. Dies ist vor allem leicht bei Verfahren möglich, deren Treffermenge durch einen Parameter gesteuert werden kann. Dieses Diagramm erfüllt einen ähnlichen Zweck wie die oben beschriebene ROC-Kurve, die man in diesem Zusammenhang auch als Trefferquote-Fallout-Diagramm bezeichnet.

Der (höchste) Wert im Diagramm, an dem der Precision-Wert gleich dem Treffer-Wert ist – also der Schnittpunkt des Genauigkeit-Trefferquote-Diagramms mit der Identitätsfunktion – wird der Genauigkeit-Trefferquote-Breakeven-Punkt genannt. Da beide Werte voneinander abhängen, wird auch oft der eine bei fixiertem anderem Wert genannt. Eine Interpolation zwischen den Punkten ist allerdings nicht zulässig, es handelt sich um diskrete Punkte, deren Zwischenräume nicht definiert sind.

Beispiel

In einer Datenbank mit 36 Dokumenten sind zu einer Suchanfrage 20 Dokumente relevant und 16 nicht relevant. Eine Suche liefert 12 Dokumente, von denen tatsächlich 8 relevant sind.

	Relevant	Nicht relevant	Summe
Gefunden	08	04	12
Nicht gefunden	12	12	24
Summe	20	16	36

Trefferquote und Genauigkeit für die konkrete Suche ergeben sich aus den Werten der Wahrheitsmatrix.

Trefferquote: ⁸⁄₍₈₊₁₂₎ = ⁸⁄₂₀ = ²⁄₅ = 0,4
Genauigkeit: ⁸⁄₍₈₊₄₎ = ⁸⁄₁₂ = ²⁄₃ ≈ 0,67
Fallout: ⁴⁄₍₄₊₁₂₎ = ⁴⁄₁₆ = ¹⁄₄ = 0,25

Praxis und Probleme

Ein Problem bei der Berechnung der Trefferquote ist die Tatsache, dass man nur selten weiß, wie viele relevante Dokumente insgesamt existieren und nicht gefunden wurden (Problem der unvollständigen Wahrheitsmatrix). Bei größeren Datenbanken, bei denen die Berechnung der absoluten Trefferquote besonders schwierig ist, wird deswegen mit der relativen Trefferquote gearbeitet. Dabei wird die gleiche Suche mit mehreren Suchmaschinen durchgeführt, und die jeweils neuen relevanten Treffer werden zu den nicht gefundenen relevanten Dokumenten addiert. Mit der Rückfangmethode kann abgeschätzt werden, wie viele relevante Dokumente insgesamt existieren.

Problematisch ist auch, dass zur Bestimmung von Trefferquote und Genauigkeit die Relevanz eines Dokumentes als Wahrheitswert (ja/nein) bekannt sein muss. In der Praxis ist jedoch oft die Subjektive Relevanz von Bedeutung. Auch für in einer Rangordnung angeordnete Treffermengen ist die Angabe von Trefferquote und Genauigkeit oft nicht ausreichend, da es nicht nur darauf ankommt, ob ein relevantes Dokument gefunden wird, sondern auch, ob es im Vergleich zu nicht relevanten Dokumenten genügend hoch in der Rangfolge eingeordnet wird. Bei sehr unterschiedlich großen Treffermengen kann die Angabe durchschnittlicher Werte für Trefferquote und Genauigkeit irreführend sein.

Weitere Anwendungsbeispiele

HIV in der BRD

Das Ziel eines HIV-Tests sollte die möglichst sichere Erkennung eines Infizierten sein. Aber welche Konsequenzen ein falsch positiver Test haben kann, zeigt das Beispiel eines Menschen, der sich auf HIV testen lässt und dann aufgrund eines falsch-positiven Ergebnisses Suizid begeht.

Bei einer angenommenen Genauigkeit von 99,9 % des nicht-kombinierten HIV-Tests sowohl für positive als auch negative Ergebnisse (Sensitivität und Spezifität = 0,999) und der aktuellen Verbreitung von HIV (Stand 2009) in der deutschen Bevölkerung (82.000.000 Einwohner, davon 67.000 HIV-positiv) wäre ein allgemeiner HIV-Test verheerend: bei nicht-kombiniertem HIV-Test würden nämlich von 67.000 tatsächlich Erkrankten lediglich 67 HIV-Infizierte fälschlicherweise nicht erkannt, aber ca. 82.000 Personen würden fälschlicherweise als HIV-positiv diagnostiziert. Von 148.866 positiven Ergebnissen wären etwa 55 % falsch positiv, also mehr als die Hälfte der positiv Getesteten. Somit liegt die Wahrscheinlichkeit, dass jemand, der nur mit dem ELISA-Test positiv getestet würde, auch wirklich HIV-positiv wäre, bei nur 45 % (positiver Vorhersagewert). Dieser angesichts der sehr geringen Fehlerrate von 0,1 % niedrige Wert liegt darin begründet, dass HIV nur bei etwa 0,08 % der Bundesbürger auftritt.

ELISA-Test	HIV positiv	HIV negativ	Summe
HIV-Test positiv	66.933	81.933	148.866
HIV-Test negativ	67	81.851.067	81.851.134
Summe	67.000	81.933.000	82.000.000

Herzinfarkt in den USA

In den USA werden pro Jahr etwa vier Millionen Frauen und Männer wegen Schmerzen in der Brust unter der Verdachtsdiagnose Herzinfarkt in eine Klinik eingewiesen. Im Verlauf der aufwendigen und teuren Diagnostik stellt sich dann heraus, dass von diesen Patienten nur etwa 32 % tatsächlich einen Infarkt erlitten haben. Bei 68 % war die Diagnose Infarkt nicht korrekt (falsch positive Verdachtsdiagnose). Andererseits werden in jedem Jahr etwa 34.000 Patienten aus dem Krankenhaus entlassen, ohne dass ein tatsächlich vorhandener Herzinfarkt erkannt wurde (ca. 0,8 % falsch negative Diagnose).

Auch in diesem Beispiel ist die Sensitivität der Untersuchung ähnlich hoch, nämlich 99,8 %. Die Spezifität lässt sich nicht ermitteln, weil die falsch-positiven Ergebnisse der Untersuchung nicht bekannt sind. Bekannt sind nur die falsch-positiven Eingangsdiagnosen, die auf der Angabe „Herzschmerz“ fußen. Betrachtet man ausschließlich diese Eingangsdiagnose, dann ist die Angabe der 34.000 Patienten, die fälschlich entlassen werden, wertlos, denn sie haben hiermit nichts zu tun. Man benötigt nämlich die Zahl der Falsch-Negativen, also jener Personen mit Herzinfarkt, die nicht eingewiesen wurden, weil sie keinen Herzschmerz hatten.

Siehe auch

Literatur

Allgemein

Hans-Peter Beck-Bornholdt, Hans-Hermann Dubben: Der Hund, der Eier legt. Erkennen von Fehlinformation durch Querdenken. ISBN 3-499-61154-6.
Gerd Gigerenzer: Das Einmaleins der Skepsis. Berliner Taschenbuch Verlag, Berlin 2004, ISBN 3-8333-0041-8.

Information Retrieval

John Makhoul, Francis Kubala, Richard Schwartz und Ralph Weischedel: Performance measures for information extraction. In: Proceedings of DARPA Broadcast News Workshop. Herndon, VA Februar 1999, S. 249–252 (psu.edu).
R. Baeza-Yates und B. Ribeiro-Neto: Modern Information Retrieval. New York 1999, ACM Press, Addison-Wesley, ISBN 0-201-39829-X, Seiten 75 ff.
Christa Womser-Hacker: Theorie des Information Retrieval III: Evaluierung. In R. Kuhlen: Grundlagen der praktischen Information und Dokumentation. 5. Auflage. Saur, München 2004, Seiten 227–235. ISBN 3-598-11675-6, ISBN 3-598-11674-8
C. V. van Rijsbergen: Information Retrieval. 2nd Edition. Butterworth, London / Boston 1979, ISBN 0-408-70929-4.
Jesse Davis und Mark Goadrich: The Relationship Between Precision-Recall and ROC Curves. In: 23rd International Conference on Machine Learning (ICML), 2006. doi:10.1145/1143844.1143874

Weblinks

Wie gut ist ein SARS-CoV-2 Testresultat? Interaktive Veranschaulichung eines binären Klassifikators von der Projektgruppe Wissenschaftskommunikation (P1) des Robert Koch-Instituts
Corona-Schnelltest-Ergebnisse verstehen. Infografik des Robert Koch-Institut mit Vergleich von hohen und niedrigen Inzidenzen. (Memento vom 18. November 2020 im Internet Archive)
Leseprobe aus Gerd Gigerenzer: Das Einmaleins der Skepsis
Information Retrieval – C. J. van Rijsbergen 1979
Tücken der Statistik: Denken Sie immer falsch positiv! (fiktives Scharlach-Screening als anschauliches Beispiel)
Anschauliche Beschreibung der Problematik von Fehlschlüssen
Diagnostisches Testen am Beispiel erklärt

Einzelnachweise

Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/ Heidelberg 2018, ISBN 978-3-662-56657-2, S. 192
Thomas G. Dietterich: Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. In: Neural Computation. Band 10, Nr. 7, 1. Oktober 1998, S. 1895–1923, doi:10.1162/089976698300017197.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/ Heidelberg 2018, ISBN 978-3-662-56657-2, S. 192

[2] Thomas G. Dietterich: Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. In: Neural Computation. Band 10, Nr. 7, 1. Oktober 1998, S. 1895–1923, doi:10.1162/089976698300017197.