Sekundentheodolit
Als Sekundentheodolit wird in der Geodäsie ein besonders genauer, aber noch handlicher Theodolit bezeichnet. Er ist eine Entwicklung aus dem ersten Drittel des 20. Jahrhunderts, doch kam der Begriff erst um 1950 auf – unter anderem durch die bahnbrechenden Entwicklungen des genialen Mechanikers Heinrich Wild.
Der Instrumententyp entstand durch die Weiterentwicklung des großen (noch offen gebauten) Triangulationstheodoliten, der wie sein mit geschlossenem Gehäuse gebauter Nachfolger eine Messgenauigkeit um ±1″ hatte.

Zur Erfolgsgeschichte des Sekundentheodolits
Entscheidend für die gleiche Genauigkeit bei etwa einem Drittel der Masse (z. B. DKM2-A nur rund 5 kg) waren unter anderem folgende Faktoren:
Entscheidende Verbesserungen von 1900 bis 1950
- Die geschlossene Hülle, die thermische Einflüsse auf die Alhidade, die Fernrohrachsen und die metallenen Bauteile der Ablesung stark verringerte.
- Die bessere Anbringung der Libellen (auch gute Libellen wandern um ca. ein Pars (etwa 10–30″) zur Seite, wenn sich eines ihrer Enden gegenüber dem anderen durch die Sonnenstrahlung um 1° erwärmt)
- bessere Konstruktionen der Stehachse und der Kippachse
- mechanisch und thermisch stabiler montierte Rektifikationsschrauben, z. B. für die optische Achse (Kollimations- bzw. Zielachsenfehler)
- Teilkreise aus Glas (statt Metall mit Silbereinlage), die auch geringere zyklische und zufällige Fehler hatten
- Ersatz der offenen, mit Nonius ausgerüsteten Ablesemikroskope und Meßspindeln – der sog. Mikrometerschrauben – durch abgedeckte, teilweise optisch arbeitende Ablesefernrohre
- das von H. Wild um 1930 erfundene Doppelkreis-Prinzip für die abzulesende Richtung (erstmals beim DKM1 realisiert, der daraufhin so klein wie ein Reisetheodolit konstruiert werden konnte. Er war genau deshalb kein großer Markterfolg, denn viele Geodäten zweifelten an seiner Genauigkeit).
Astronomische Vorläufer-Instrumente: ortsfest und gekühlt
Vorläufer der zur Mitte des 19. Jahrhunderts zum Einsatz kommenden Triangulations- und astronomischen Theodolite waren im Wesentlichen die großen Universalinstrumente, die wiederum konstruktiv bei den Passageninstrumenten und den Meridiankreisen der Observatorien Anleihen genommen hatten. Da aber ein astronomisches Instrument i. A. keinen großen Schwankungen der Temperatur ausgesetzt ist (die Kuppeln der Sternwarten bleiben tagsüber relativ kühl) und auch nur selten transportiert werden, sind die thermisch verursachten Nachteile der ersten Triangulationstheodolite (um 1850) nur allzu verständlich. Immerhin kamen bis dato fast alle berühmten Geodäten (z. B. Gauß, Bouguer, Cassini, Lambert und die „Stars“ der Pariser Akademie) aus dem Kreis der Astronomen oder Mathematiker.
Für technische Neuerungen trugen neben einigen optisch sehr versierten Feinmechanikern auch die Erfahrungen mit dem geodätischen Außendienst-Einsatz von kleinen Instrumenten bei, so durch einige perfekt konstruierte Bauteile von damaligen Dioptern und der Kippregel, durch Weiterentwicklungen des Azimutalquadranten (Prototypen bereits um 1500), der Bordaschen Instrumente und einigen – heute in völlige Vergessenheit geratenen – Sonderkonstruktionen. Etwa gleichzeitig mit den „Sekunden-fähigen“, aber nun tragbaren Universal-Messgeräten wurden auch Repetitionstheodolite entwickelt, mit denen man durch Addition von Winkeln die Messgenauigkeit auf das Zwei- bis Dreifache erhöhen konnte.
Optische und elektronische Streckenmessung
Bis zum Anfang des 20. Jahrhunderts waren die Theodolite nur für Winkel-, nicht aber für Streckenmessung geeignet. Doch kamen mit der Etablierung moderner Maschinen- und Bautechniken, die dem Instrumentenbau kräftige Impulse gaben, geodätische Instrumente auf den Markt, die mit Zusätzen für die optische Entfernungsmessung ausgerüstet waren. Sie arbeiteten durch Messung des parallaktischen Winkels an einer Zwei-Meter-Basislatte und splitteten sich bald in solche mit horizontaler und vertikaler Messlatte auf: erstere erzielten höhere Genauigkeit und wurden für die Landesvermessung eingesetzt, letztere in der Bauvermessung und der Ingenieurgeodäsie. Heute sind diese Geräte – obwohl sie auch nach 50 Jahren noch klaglos funktionieren – zu reinen Liebhaber- oder Museumsstücken geworden, denn sie konnten sich gegen die in den 1960er-Jahren aufkommenden elektronischen „Distanzer“ (auf Basis von Mikrowellen, Infrarot und bald auch Lasern) nicht lange behaupten.
Näheres kann u. a. im Dortmunder Museum für Vermessungstechnik (Förderkreis Vermessungstechnisches Museum e. V., D-44137 Stadt Dortmund) in Erfahrung gebracht werden, auf dessen Webseiten einige der erwähnten Konstruktionen in guten Fotos dokumentiert sind. Genaue Universalinstrumente wurden ab 1850 für Triangulation und Astronomie gebaut.
Heutige Sekundentheodolite
Unter- und Oberbau
Ein moderner Sekundentheodolit hat zwar prinzipiell fast denselben Aufbau wie die bis gegen 1950 verkauften „Schraubendampfer“ (ein von TU-Studenten geprägter Spitzname). Die geschlossene Bauweise macht ihn jedoch 1) genauer, 2) thermisch stabiler und 3) weniger anfällig für Stöße. In den 1970er Jahren war der „Star“ einer Geodäsie-Messe ein Wild T2, der in seiner Metallbombe einen Sturz über eine 100 Meter hohe Felswand „überlebt“ hatte. Er musste von Wild Heerbrugg nur geringfügig nachjustiert werden. Der Behälter sah allerdings aus wie eine Ziehharmonika.
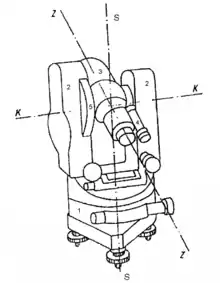
Der Theodolit-Unterbau oder Limbus (meist etwas konisch ausgeführt) enthält den Horizontalkreis (1) und die vertikale Stehachse (S). Darauf ist die Alhidade drehbar gelagert – der sog. Oberbau, zwischen dessen Stützen (2) sich das Messfernrohr (3) um die horizontale Kippachse (K) drehen lässt. Für beide Achsen gibt es jeweils eine Klemmung und eine Feinbewegung. Letztere ist oft zweigängig ausgeführt, um sehr feine Einstellungen zu ermöglichen. Die Ablesung der zum jeweiligen Zielpunkt eingestellten Winkel erfolgt optisch mit 2 × 2 Planplatten und zugehörigen Mikrometern, die etwa an den mit (4) und (5) sitzen.
Das Fernrohr hat eine Apertur um die 40 mm, eine Vergrößerung von 30–35 fach und ein Fadennetz, das eigentlich eine mikrofotografisch hergestellte oder elektronisch geätzte Strichplatte ist. Dieses äußerst präzise Glasplättchen (engl. reticule) befindet sich bei optisch unendlich entfernten Zielen im gemeinsamen Brennpunkt von Objektiv und Okular. Ist der Zielpunkt (ob Detail- oder Polygonpunkt, Messlatte oder Bodenpunkt, tut optisch nichts zur Sache) näher als etwa 100 Meter, ist er durch eine Innenfokussierung scharfzustellen. Zu diesem Zweck ist im hinteren Fernrohrviertel eine Fokussierlinse eingebaut, die sich mit einem äußerst präzise gefertigten Innenzylinder genau entlang der Zielachse (Z) verschieben lässt. Die Fokussierschraube sitzt meist am Oberrand des Fernrohrs oder ist als griffiger, auch bei Nacht leicht zu findender Rändelring ausgeführt. Sie verschiebt nicht mehr (wie bei den Theodoliten vor 1950) den Okularteil mit der Strichplatte, sondern ändert die Brennweite des Objektivs.
Anmerkung zur potentiellen Messgenauigkeit
Die Verschiebung der inneren Fokussierlinse kann nicht völlig linear erfolgen. Daher hierzu eine Anmerkung, die sich für erfahrene Beobachter erübrigt: Obwohl alle diese mechanisch-optischen Bauteile mit Toleranzen unter etwa ein µm gefertigt sind, gibt es immer eine geringe Abweichung aus der optischen Achse (siehe auch Alignement), bzw. einen Totgang. Um die 1″-Genauigkeit wahren zu können, muss der Geodät die letzte feine Drehung der Fokussierung immer im selben Sinn (üblicherweise im Uhrzeiger) tun. Andernfalls kommt es zu systematischen Zielfehlern, die etwa 3–5″ erreichen können. Auch eine häufige Scharfstellung zwischen verschieden entfernten Messpunkten ist ungünstig, wenn man letzte Genauigkeit (etwa 0,5 mm auf 100–200 Meter) erreichen will. Besser ist es, eine geringe Unschärfe in Kauf zu nehmen und dafür das messende Auge genau in der optischen Achse zu halten (leicht erkennbar am symmetrischen Gesichtsfeld). Bei Blendung durch starken Sonnenschein oder bei schlechtem Kontrast der angezielten Punkte usw. ist diese Arbeitsweise natürlich erschwert.
Eine andere Methode, um diese optisch unvermeidliche kleine Fehlerquelle zu umgehen, wäre die Messung der Detailpunkte in einer Art ringförmigen Abfolge (d. h., der Figurant stellt die Messlatte nicht auf die räumlich hintereinander einzumessenden Punkte, sondern umkreist den überm Polygon- oder Festpunkt aufgestellten Theodolit auf 1–3 Ringwegen). Dagegen spricht aber die anzustrebende Sequenzierung der Messungen, und dass die restlichen Kreisteilungsfehler und Rutscheffekte etwas mehr wirksam werden könnten.
Denn die Punktfolge muss meistens kodiert werden (Straßenrand, Einbauten, Hausecken usw.) oder zumindest auf der Feldskizze in eine gute Ordnung gebracht werden, um nichts zu vergessen. Am besten ist es – auch im Sinne der Wirtschaftlichkeit – wenn der Ingenieur schon länger vor Beginn der Messungen die Wahl der geeignetsten Messmittel und Messmethoden erkundet und sich allenfalls mit alternativen Programmen im Theodolitsystem vertraut macht. Auch muss es nicht immer der bewährte Polygonzug mit anschließender Polaraufnahme sein: Manchmal ist die freie Stationierung des Messgerätes vorzuziehen, oder eine zwei- statt einfacher Kontrolle mit Sperrmaßen, oder bei besonders heiklen Projekten ein Netzausgleich. Entsprechende Erfahrung vorausgesetzt, lassen viele moderne Digitaltheodolite auch zwischendurch eine gewisse Änderung der Vorgangsweise zu.
Stativ und Aufstellung
Der Unterbau des Theodolits sitzt auf der Grundplatte, die am Stativ aufgesetzt und mit drei Fußschrauben und der Libelle auf der Alhidade (zwischen den zwei Fernrohrstützen) genau horizontiert wird.
Erfolgt dies zu flüchtig, bei starker Sonnenstrahlung oder unter Vibrationen (z. B. auf einer Brücke), so bleibt ein merklicher Stehachsenfehler zurück. Er wirkt ähnlich wie eine Lotabweichung (die allerdings nur in steilem Gelände eine wesentliche Rolle spielt). Wenn dieser an sich unvermeidliche Aufstellungsfehler z. B. δ = 10″ beträgt (typisch bei einer Alhidadenlibelle mit Parswert 20″), so bewirkt die nicht genaue Stehachse einen Messfehler, der mit dem Tangens des Höhenwinkels h ansteigt. Bei 10″ wird also wegen δ·tanh < 1″ bereits ab Höhenwinkeln von h = 5,7° etwas von der Genauigkeit eines Sekundentheodolits „verschenkt“.
Neben der horizontalen Aufstellung ist auch die genaue Zentrierung über dem Polygon- oder Vermessungspunkt wesentlich. Dazu hat jeder moderne Theodolit und jedes Tachymeter ein optisches Lot – ein kleines Zielfernrohr, das bei korrekt aufgestelltem Unterbau genau in die Lotrichtung schaut. Zur Aufgabe, den Theodolit auf ebenem Gelände oder gar auf einem Steilhang aufzustellen, gibt es mehrere Methoden, die u. a. in den Hochschulskripten der Geodäsie-Institute angeführt sind (siehe z. B. Weblink Nr. 2).
Andere Typen von Theodoliten
Wie aus obigen Ausführungen zu ersehen, ist ein Sekundentheodolit oder -tachymeter für den überwiegenden Teil der Vermessungsprojekte geeignet. Dennoch ist es manchmal besser, ein weniger genaues Instrument zu wählen, wenn die Arbeit damit ausreichend genau, aber etwas schneller vonstattengeht. Für hochpräzise Netze bei technischen Großprojekten oder in einer auf < 0,1 mm einzumessenden Maschinenhalle kann aber auch ein noch genaueres Messmittel erforderlich sein. Daher folgende kleine Liste:
- Bautheodolit: sehr robust, leicht, einfach zu bedienen (ca. ±10″)
- Tachymeter: mit integriertem Entfernungsmesser (Reichweite einige Hektometer). Hat seit etwa 1990 digitale Ablesung und eine automatische Neigungskompensation der Stehachse (neuere Sekundentheodolite ebenfalls). Winkelgenauigkeit etwa ±2″ oder ±1 mm auf 100 m.
- Präzisions- oder Sekundentheodolit (±1″, für 90 % der Ingenieurgeodäsie)
- Robotik-Theodolit (automatisch oder funkgesteuert), Genauigkeit um ±1″; ideal für ständige Überwachungs-Aufgaben wie Deformationsmessungen an großen oder sensiblen Bauten, für Kohlen-Tagebaue oder für drohende Felsstürze, Hangrutschungen etc.
- Universalinstrument, z. B. DKM3 und Wild T4 (bis zu ±0,2″) für Präzisionsnetze, seltenere, aber extreme Deformationsmessungen etwa von Staumauern, Kühltürmen oder Hochhäusern, ferner für die Astrogeodäsie, früher auch für Stellartriangulation. Mit entsprechendem Aufwand sind terrestrische Netze auf ±1 mm pro Kilometer möglich, doch wird man solche Vorgaben heute eher mit GPS angehen.
- Theodolit-ähnlich gebaut sind auch manche Passageninstrumente und Sondergeräte für Militär- und Satellitengeodäsie (z. B. das Moonwatch-Apogee oder die früheren Kinetheodolite). Sie sind teilweise auch zur Verfolgung rascher Bewegungen ausgelegt, aber mit geringerer Genauigkeit (bis etwa 5″).
Typische Größe der Instrumentenfehler
Bei jedem Theodolit spielen 4 Arten von feinmechanischen bzw. operativen Fehlern eine Rolle, die sich nur teilweise verringern lassen:
- Stehachsenfehler (operationell): nur durch sorgfältiges Horizontieren klein zu halten, oder nachträgliche Reduktion (über Libellen oder Kompensatoren)
- Kippachsenfehler (Justier- bzw. Herstellungsfehler): Kippachse des Fernrohrs nicht exakt senkrecht zur Stehachse, großteils eliminierbar durch zwei Kreislagen.
- Zielachsenfehler (heikler Justierfehler), wenn die optische Achse des Fernrohrs nicht exakt senkrecht auf seine Kippachse steht. Zu etwa 90 % eliminierbar durch zwei Kreislagen.
- Höhenindexfehler: Der Nullpunkt für die Zenitwinkelmessung liegt nicht genau in der Lotrechten. Großteils eliminierbar durch Versicherungslibelle (bei älteren Instrumenten) oder durch gravitative Kompensatoren (ein- oder zweiachsig bzw. mit öligen Fluidspiegeln).
Weitere Steigerungen der Messgenauigkeit sind möglich durch
- wiederholtes Messen, insbesondere mit verschiedenen Teilkreisstellungen
- Bei mehreren Sätzen; nach der Hälfte den Theodolit am Stativteller um 180° verdrehen (Reduzieren der Taumelfehler der Stehachse)
- oder (nach vorheriger Analyse der Achsfehler) durch nachträgliche Reduktion berücksichtigen.
Beobachtung und Genauigkeit: Zur Fehlereliminierung werden die Ziele in einem so genannten Satz oder in gemessen (manchmal auch in Halbsätzen, etwa bei Messungen zur Sonne). Ein Satz besteht dabei aus zwei Messreihen (zwei Halbsätzen), wobei für die zweite Messreihe das Fernrohr durchgeschlagen (um die Kippachse zur anderen Geräteseite gedreht) wird, der Oberbau um 180° gedreht und die Ziele erneut anvisiert wird. Dadurch erfolgen die Ablesungen der Zielrichtungen an gegenüberliegenden Stellen der Teilkreise (also mit etwa 180° = 200 Gon Differenz), wodurch der Geodät einige der immer vorhandenen, kleinen systematischen Fehler bei der Winkelberechnung eliminieren kann. Einige andere lassen sich von erfahrenen Beobachtern verringern, etwa gewisse Fehlereinflüsse der Kreisteilung, der Fernrohrbiegung und diverse thermische Fehler.
Was den Gegenstand der Beobachtungen betrifft, unterscheidet man
- Horizontalwinkel: Ein Horizontalwinkel besteht aus Richtungsbeobachtungen zu mindestens zwei Zielen,
- Zenitwinkel: (Zenitdistanz) oder auch Vertikalwinkel,
- Winkeldifferenzen: Entfernungsmessung mit Reichenbachfäden, gewisse Kontrollmessungen
- Messung mit beweglichem Fadennetz: nur bei speziellen Theodoliten, siehe unpersönliches Mikrometer.
Theodolite, die auch eine elektronische Entfernungsmessung erlauben (abgekürzt EDM, heißen Tachymeter oder – bei Ausrüstung mit GIS-Modulen oder mit GPS – auch Totalstationen).