Parkettierung mit Fünfecken

Die Parkettierung mit Fünfecken (auch Kachelung/Pflasterung/Flächenschluss mit Pentagonen) ist eine lückenlose, überlappungsfreie geometrische und monohedrale Parkettierung, bei der alle Elemente (Kacheln) kongruent (deckungsgleich) zueinander und von der Form eines und desselben Fünfecks sind.

Die 15 bisher bekannten Typen der ebenen Parkettierung mit kongruenten, konvexen Fünfecken

Der Fall der ebenen Parkettierung mit kongruenten (deckungsgleichen), konvexen Fünfecken ist deshalb besonders interessant, weil die in Frage kommenden Formen (Typen) seit einem Jahrhundert untersucht werden, diese nicht abschließend klassifiziert sind und 5 der derzeit bekannten 15 verschiedenen Typen von der Amateur-Mathematikerin Marjorie Rice und einem Informatiker gefunden wurden, die durch Artikel von Martin Gardner in der populärwissenschaftlichen Zeitschrift Scientific American zu ihren Nachforschungen inspiriert worden waren.

Monohedrale Parkettierung mit n-Ecken (n = 3, n = 4, n ≥ 6)

Im Gegensatz zu den Fünfecken ist die Frage der monohedralen Parkettierung der Ebene mit n-Gonen für n≠5 vollständig geklärt.

Alle Formen von Dreiecken[A 1] und konvexen Vierecken „parkettieren die Ebene“ (englisch „tile the plane“).

Bezüglich der Polygone mit einer Eckenzahl $n\geq 6$ bewies Reinhardt bereits 1918,[1] dass es einerseits genau drei Typen von konvexen Sechsecken (Hexagonen) gibt, die parkettieren können, und dass es andererseits unmöglich ist, die Ebene mit einem konvexen Siebeneck (Heptagon), Achteck (Oktagon) oder einem höheren Polygon zu parkettieren.

Monohedrale Parkettierung der Ebene mit Fünfecken

Im Gegensatz zu den Parkettierungen mit anderen konvexen Polygonen ist die Parkettierung der Ebene mit Fünfecken noch nicht abschließend geklärt. Siehe auch Abschnitt über die Arbeiten von Michaël Rao.

Bezeichnungen

Bei der monohedralen Parkettierung fordert man Kongruenz unter den parkettierenden Kacheln, jedoch mit der Protokachel nur Ähnlichkeit. Abhängig von der Anzahl der Freiheitsgrade des Kacheltyps kann es unähnliche Protokacheln geben, die zum selben Kacheltyp gehören. Der Kacheltyp ist durch ein System von Beziehungen zwischen Winkeln einerseits und Seitenverhältnissen andererseits charakterisiert. Zu einem Kacheltyp kann es Parkettierungen geben, die sich in wesentlichen Eigenschaften unterscheiden.

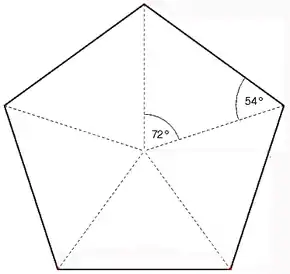
Ein kongruentes Fünfeck ist durch sieben Bestimmungsstücke (7 unabhängige Parameter) bestimmt, ein ähnliches durch sechs. Bei ähnlichen Fünfecken sind Längenverhältnisse (von sich entsprechenden Seiten und Diagonalen) und sich entsprechende Winkel gleich. Hat man vier (Eck-)Winkel, dann ist der fünfte immer durch die Winkelsumme des Fünfecks von 540° bestimmt.

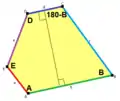
Im Folgenden werden die (Größen der) Winkel mit großen lateinischen Buchstaben A, B, C, D, E bezeichnet, so dass A+B+C+D+E = 540° ist. Die Orientierung ist standardmäßig die „mathematische“, also entgegen dem Uhrzeigersinn (obwohl es viele Typen gibt mit Parkettierungen, in denen beide Orientierungen vorkommen). (Die Längen von) Seiten, die in diesem Umlaufsinn auf eine Ecke zulaufen, werden üblicherweise mit dem entsprechenden kleinen Buchstaben bezeichnet, so dass bspw. b die Länge der Seite AB ist.

Die Geschlossenheit des Polygonzugs BCDEAB erfordert:

c cos(B) – d cos(B+C) + e cos(B+C+D) + a cos(–A) = b und

c sin(B) – d sin(B+C) + e sin(B+C+D) + a sin(–A) = 0 .

Geschichtliches

Nach der Dissertation von Reinhardt, der 1918 die ersten 5 Fünfeck-Typen beschrieb,[1] vergingen 50 Jahre, bis das Thema ab den späten 1960er bis in die Mitte der 1980er Jahre wieder aufgenommen und um neun Typen erweitert wurde. Danach vergingen 30 Jahre, bis mit einem eigens zu diesem Zweck erstellten Computerprogramm 2015 ein weiterer Fünfeck-Typ, Typ 15, gefunden wurde. Man kann die konvexen Fünfecke, die geeignet sind, eine Ebene in kongruenter Weise zu parkettieren, in bisher 15 disjunkte Klassen (Typen) einteilen.[2]
Es ist derzeit aber nicht geklärt, ob es noch mehr solcher Typen von Fünfecken gibt.

Regelmäßiges Fünfeck

Dennoch sind Aussagen zu speziellen Aspekten gemacht worden:

Die Parkettierung einer euklidischen Ebene mit regelmäßigen Fünfecken ist unmöglich, da bei einem regelmäßigen Fünfeck der Innenwinkel 108° kein ganzzahliger Teiler des Vollwinkels 360° ist.
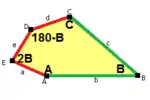
Hirschhorn und Hunt publizierten 1985 Zusammenhänge für Winkelsummen, die essenzielle Bedingungen für die Parkettierung mit Fünfecken sind: Ein gleichseitiges konvexes Fünfeck parkettiert dann und nur dann, wenn es zwei Winkel besitzt, deren Summe 180° ist, oder wenn es das einzigartige gleichseitige konvexe Fünfeck ist, welches (in den Bezeichnungen des Typs 7 in der nachfolgenden Tabelle) die Winkel A≈99,929°, B≈89,264°, C≈144,561°, D≈70,878° und E≈135,368°[A 2] besitzt, wobei B+2E = 2C+D = 2A+B+D = 360°.[3]
Olga Bagina konnte zeigen, dass es nur 8 konvexe Kante-an-Kante-Parkettierungstypen (edge-to-edge tiling) geben kann,[4][5] ein Resultat, das mit Referenz auf Bagina, aber in unabhängiger Weise von Teruhisa Sugimoto[6] bestätigt wurde.

Im Folgenden werden die 15 bekannten Typen monohedraler Parkettierung der Ebene mit Fünfecken ungefähr in ihrer Entdeckungsreihenfolge resp. mit aufsteigender Typennummer vorgestellt.

Reinhardt (1918)

Die fünf konvexen Fünfeck-Typen von K. Reinhardt (1918)[A 3]
1	2	3	4	5
p2 (2222)	pgg (22×)	p3 (333)	p4 (442)	p6 (632)

B+C=180° A+D+E=360°[A 4]	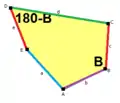c=e B+D=180°	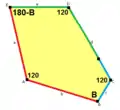a=b, d=c+e A=C=D=120°	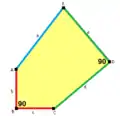b=c, d=e B=D=90°	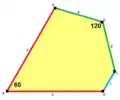a=b, d=e A=60°, D=120°
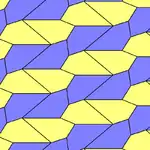
2er-Kachelmuster	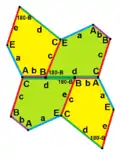4er-Kachelmuster	3er-Kachelmuster	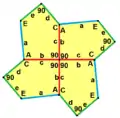4er-Kachelmuster	6er-Kachelmuster

Im Jahr 1918 beschäftigte sich Karl Reinhardt, Assistent von David Hilbert, in seiner Dissertation[1] mit der „Zerlegung einer Ebene in gleicheckige, einer Gattung angehörige Normalpolygone“, wobei er besonders Fünf- und Sechsecke behandelte.

Kershner (1968) und James (1975)

Konvexe Fünfeck-Typen
von R. B. Kershner (1968) und R. E. James (1975)[A 3]
6	7	8	10
p2 (2222)	pgg (22×)		p2 (2222)

a=d=e, b=c B+D=180°, 2B=E	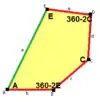b=c=d=e B+2E=2C+D=360°	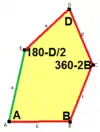b=c=d=e 2B+C=D+2E=360°	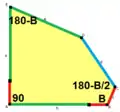a=b=c+e A=90, B+E=180° B+2C=360°[A 5]
4er-Kachelmuster	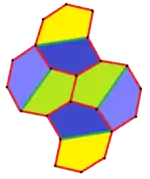8er-Kachelmuster	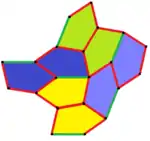8er-Kachelmuster	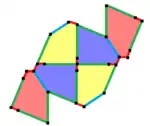6er-Kachelmuster
Richard B. Kershner			Richard E. James

Der Mathematiker Richard B. Kershner fand 1968 drei weitere konvexe Fünfecke (Typen 6 bis 8), mit denen Parkettierung möglich ist, und kam zu der Überzeugung, dass mit den nun bekannten acht Typen die Liste von ebenen, parkettierungsfähigen Fünfecken komplett sei.[7]

Richard E. James III, damals Informatiker bei der Control Data Corporation, hatte von Kershners Entdeckung in Martin Gardners Kolumne Mathematical Games in Scientific American gelesen und daraufhin 1975 ein weiteres Fünfeck (Typ 10) gefunden,[8][9] wodurch er Kershners Aussage der kompletten Liste widerlegte. Durch den Ansatz von James konnte auch im Nachhinein erklärt werden, welches Parkettierungssystem Kershner übersehen hatte.[10]

Rice (1976/77)

Die vier konvexen Fünfeck-Typen von Marjorie Rice (1976/77)[A 3]
9	11	12	13
pgg (22×)

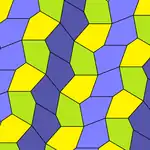b=c=d=e 2A+C=D+2E=360°	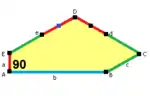2a+c=d=e A=90°, 2B+C=360° C+E=180°	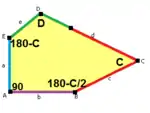2a=d=c+e A=90°, 2B+C=360° C+E=180°	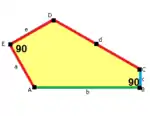d=2a=2e B=E=90°, 2A+D=360°
8er-Kachelmuster	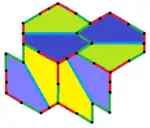8er-Kachelmuster	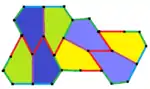8er-Kachelmuster	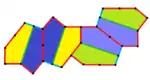8er-Kachelmuster

Angeregt durch Martin Gardners Kolumne Mathematical Games in Scientific American im Juli und Dezember 1975, begann Marjorie Rice, Hausfrau[11] und Autodidaktin in Bezug auf mathematische Geometrie, sich mit Parkettierung mit Fünfecken zu beschäftigen. Sie entwickelte ihre eigene Notation für Fünfecke und fand auf diese Weise eine weitere, bisher unbekannte Fünfeckform (Typ 9), die sie Gardner zuschickte.
Gardner leitete die Arbeit von Rice weiter an die Mathematik-Professorin Doris Schattschneider, die mit Rice in Kontakt trat und in den folgenden Jahren Rices Ergebnisse publizierte.[10][12]

In den Jahren 1976/77 entdeckte Rice mit ihrer Methode insgesamt vier neue Pentagon-Typen. Sie setzte Fünfeck-Typen auch künstlerisch um, indem sie Escher-artige Bildelemente auf diese Fünfecke übertrug:[13] Beispiele sind Typ 1,[14] Typ 2[15] und Typ 13.[16]

Der Eingangsbereich des Hauptgebäudes der Mathematical Association of America in Washington, D.C. wurde in den 1990er Jahren mit einem der von Rice gefundenen Fünfecke gefliest.[17]

Stein (1985) und Mann / McLoud / Von Derau (2015)

Konvexe Fünfecke von R. Stein (1985) und C. Mann / J. McLoud / D. Von Derau (2015)[A 3]
14	15
p2 (2222)	pgg (22×)

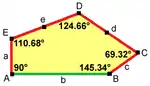2a=2c=d=e A=90°, D=cos⁻¹(^3−√57⁄₈)≈124,66° B=270°−D, C=360°−2B	a=c=e, b=2a, d=a√2+√3 A=150°, B=60° C=135°, D=105°, E=90°
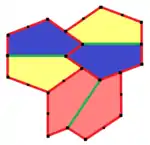6er-Kachelmuster	12er-Kachelmuster
Stein (1985)	Mann/McLoud/ Von Derau (2015)

Der deutsche Mathematikstudent Rolf Stein[18] fand 1985 den Typ 14, der in Folge von Schattschneider analysiert und publiziert wurde.[12] Seine Kacheln sind vollständig bestimmt.

2015 entdeckten das Mathematiker-Ehepaar Casey Mann und Jennifer McLoud sowie deren Student David Von Derau von der University of Washington in Bothell mittels eines Computerprogramms einen 15. Typ.[19][11][20]

Sie berücksichtigten dabei die Ergebnisse von Hirschhorn und Hunt[3] sowie von Bagina[4] und verwendeten einen Algorithmus, der nach Parkettierungen mit nicht gleichseitigen Fünfecken suchte, die nicht Kante-an-Kante sind.[21] Von Derau implementierte das Programm und bereits in der Debugging-Phase wurde das neue Fünfeck, Typ 15, gefunden.

Michaël Rao (2017)

Dass zwei Jahre lang kein weiteres Fünfeck gefunden wurde, kann an den Erkenntnissen von Michaël Rao liegen, wonach ein „16. Fünfeck“ nicht mehr existiert, bzw. immer nur eine Variante der bekannten 15 Fünfecke ist.[22] Da bisher noch kein wissenschaftliches Peer-Review seiner Beweisführung vorliegt (wohl aber positive Einzelmeinungen),[23] kann die Suche danach zu Ende sein – die abschließende Bestätigung steht aber derzeit noch aus.

Anzahl der Freiheitsgrade

In seiner Dissertation[1] nahm Reinhardt eine Klassifizierung[24] der Kacheltypen bezüglich der Längenverhältnisse ihrer fünf Seiten vor:

R-I Alle fünf Seiten sind verschieden.
R-II Unter den fünf Seiten sind zwei gleiche; die anderen sind von diesen und untereinander verschieden.
R-III₁ Unter den fünf Seiten sind drei gleiche; die anderen sind von diesen und untereinander verschieden.
R-III₂ Unter den fünf Seiten sind zwei Paare gleicher, untereinander aber verschiedener; die letzte ist von diesen verschieden.
R-IV₁ Unter den fünf Seiten sind vier gleiche; die letzte ist von diesen verschieden.
R-IV₂ Unter den fünf Seiten sind drei gleiche und, davon verschieden, noch zwei gleiche.
R-V Alle fünf Seiten sind einander gleich.

Alle 15 hier beschriebenen Parkettierungstypen sind isohedral, was bedeutet, dass es unter den Abbildungen der Parkettierung auf sich selbst zu jedem Paar von Kacheln eine Abbildung gibt, die eine Kachel in die andere überführt; kurz: dass die gesamte Parkettierung von jeder Kachel aus gesehen „gleich aussieht“. Viele der 15 Parkettierungstypen sind mehrfach isohedral (mehrfach transitiv).

Typ	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Freiheitsgrade[25]	5	4	1	2	2	1	1	1	1	1	1	1	1	0	0
Reinhardt-Klasse	R-I	R-II	R-II	R-III₂	R-III₂	R-IV₂	R-IV₁	R-IV₁	R-II	R-IV₁	R-II	R-I	R-II	R-III₂	R-III₁
Kante-an-Kante[A 6]	beides	beides	nein	ja	ja	ja	ja	ja	ja	nein	nein	nein	nein	nein	nein
k-isohedral[26]	1	1	1	1	1	2	2	4	2	3	2	2	2	3	3
nicht-konvex[A 7]	ja	ja	nein	ja	ja	ja	ja	ja	ja	nein	nein	nein	ja	nein	nein

Beim Kacheltyp 1 gibt es auch nichtperiodische Fünfeck-Parkettierungen.

Spezielle Fälle

Nichtperiodische Fünfeck-Parkettierung

Die Hirschhorn-Parkettierung durch kongruente Fünfecke

Auch nichtperiodische Parkettierungen lassen sich mit kongruenten Fünfecken konstruieren, wie dieses Beispiel (rechts) mit 6-zähliger Drehsymmetrie von Michael Hirschhorn illustriert mit A = 140°, B = 60°, C = 160°, D = 80°, E = 100°.[27]

2016 wurde durch Bernhard Klaassen gezeigt, dass jede Drehsymmetrie der Ebene durch eine monohedrale Parkettierung aus ein und derselben Klasse von Fünfecken repräsentiert werden kann.[28][29] Hier sind Beispiele für 5-zählige und 7-zählige Drehsymmetrie angegeben.

Zerlegungsprinzip für jede n-zählige Drehsymmetrie mit n>2
Fünfeck-Parkettierung mit 5-zähliger Drehsymmetrie	Fünfeck-Parkettierung mit 7-zähliger Drehsymmetrie

Alle diese Beispiele zeigen an Stellen, wo sich mehrere Fünfeck-Kanten zu einem Geradenstück fortsetzen lassen, dass mit der zugrunde liegenden Fünfeck-Form auch eine periodische Parkettierung möglich ist, und zwar gehört diese zum Parkettierungstyp 1.

Fünfeck-Parkettierung von Sechsecken

Fünfeck/Sechseck-Parkettierung

Einige Sechsecke können durch einfache geometrische Operationen als Parkettierung mit Fünfecken dargestellt werden.

Beispielsweise lässt sich ein regelmäßiges Sechseck durch einen seitenvertikalen Schnitt in zwei Typ-1-Fünfecke zerlegen. Weitere Unterteilung in drei (Typ 3), vier (Typ 4) und neun (Typ 3) kongruente Fünfecke ist möglich.

Duale Fünfeck-Parkettierungen

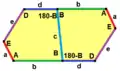
Es gibt drei isohedrale Fünfeck-Parkettierungen (d. h. Parkettierungen mit kacheltransitiver Symmetriegruppe), die dual sind zu Parkettierungen der oben gezeigten Art. Diese (dualen) Parkettierungen sind immer Kante-an-Kante und haben als Protokachel einen Spezialfall höherer Symmetrie unter den oben gezeigten 15 Kacheltypen.

Parkettierung dual zu Typ 5	Parkettierung dual zu Typ 4	Parkettierung dual zu Typ 5

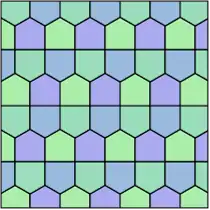Prismatische Parkettierung	Kairo-Parkettierung[A 8]	Floret- oder Rosetten-Parkettierung[A 9]
Kachel vom Typ 1[1]	Kachel vom Typ 4[1]	Kachel vom Typ 1, 2 als auch 5[1]
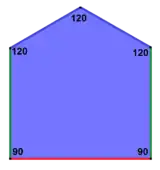120°, 120°, 120°, 90°, 90° 1 Freiheitsgrad	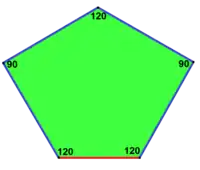120°, 90°, 120°, 90°, 120° b = c = d = e, a = b(√3-1)	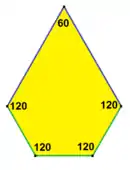60°, 120°, 120°, 120°, 120° a = b = 2c = 2d = 2e

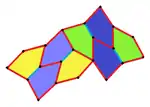
Parkettierung mit kongruenten, konkaven Fünfecken in der Ebene

Abb. Pentagon von Livio 2-isohedral

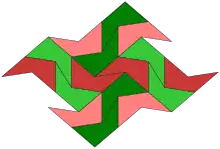
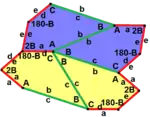
Sind die kongruenten Fünfecke konkav (also nichtkonvex), d. h., mindestens ein Innenwinkel ist überstumpf (größer als 180°), dann sind weitere Parkettierungen möglich. Ein Beispiel dafür ist das Pentagon von Livio,[A 10] zu dem Parkettierungen mit außerordentlich unterschiedlichen Topologien gefunden wurden.[30]

Auf der dortigen Seite 3 zeigt Figure 3 zwei (periodische) 1-isohedrale Parkettierungen: Zu jedem Paar von Fünfecken gibt es eine Kongruenzabbildung, die das eine Fünfeck in das andere überführt.

In der (periodischen) Parkettierung der Abbildung „Pentagon von Livio 2-isohedral“ sind den Fünfecken vier Farben zugeordnet: dunkelgrün, hellgrün, dunkelrot, hellrot. Parallelverschiebungen und Punktspiegelungen (Drehungen um 180°) bilden die Fünfecke in solche gleicher Farbe und gleicher Helligkeit ab. Die dunklen Fünfecke haben gleichen Drehsinn (der sehr spitzen Ecke folgt im Gegenuhrzeigersinn die überstumpfe) und die hellen entgegengesetzte. Mit einer Achsenspiegelung lässt sich der Drehsinn umkehren, und zwar lassen sich (mit einer zusätzlichen Parallelverschiebung) helle Fünfecke auf dunkle gleicher Farbe abbilden und umgekehrt. Es gibt aber keine Kongruenzabbildung der Parkettierung, die grüne auf rote Fünfecke abbildet, denn bei allen grünen gibt es zwei benachbarte Seiten, die sich als Geraden in die roten Nachbarfünfecke fortsetzen lassen; bei den roten gibt es auch zwei solche Seiten, die sind aber nicht benachbart. Es gibt also zwei Bahnen der Parkettierung, die Bahn der grünen und die der roten Fünfecke, weshalb die Parkettierung als 2-isohedral anzusehen ist.

Die obere rechte Abbildung der Figure 4 auf Seite 4 in Tessellations[30] zeigt eine aperiodische Parkettierung mit demselben Pentagon von Livio.

Sphinx-Parkettierung („reptile“)

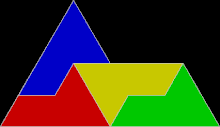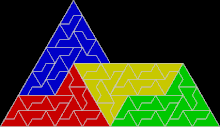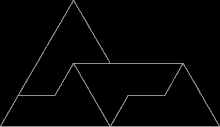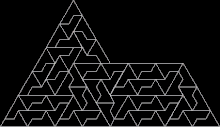
Ein anderes Beispiel ist die sogenannte Sphinx-Parkettierung, eine aperiodische Parkettierung mit einem konkaven Fünfeck, das sich aus kleineren Versionen seiner selbst parkettiert.[A 11]

Fünfeck-Parkettierung in der hyperbolischen Geometrie

Regelmäßige Fünfeck-Parkettierung

Dodekaeder

Ein Dodekaeder kann man als regelmäßige Parkettierung der Oberfläche einer Kugel mit 12 regelmäßigen Fünfecken verstehen. Das dazugehörige Schläfli-Symbol ist {5,3}, d. h., drei Fünfecke liegen aneinander und bilden jeweils eine Ecke.

Auf einer hyperbolischen Ebene gibt es unendlich viele Parkettierungen mit regelmäßigen Fünfecken, beispielsweise Parkettierung 4. Ordnung mit dem Schläfli-Symbol {5,4}, d. h., vier Fünfecke liegen aneinander und bilden jeweils eine Ecke. Höhere Ordnungen regelmäßiger Parkettierung {5,n} können in dieser Weise konstruiert werden, theoretisch bis {5,∞}.

Kugel	Hyperbolische Ebene
{5,3}	{5,4}	{5,5}	{5,6}	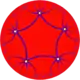{5,7}	{5,8}	…{5,∞}

Unregelmäßige Fünfeck-Parkettierung

Auf einer hyperbolischen Ebene kann es unendlich viele dualstrukturale einheitliche Parkettierungen mit isogonalen unregelmäßigen fünfeckigen Flächen geben. Nach M. Cundy und A. Rollett werden sie mit V3.3.p.3.q beschrieben.[31]

Ordnungen p-q der pentagonalen Floret-Parkettierung
7-3	8-3	9-3	…	5-4	6-4	7-4	…	5-5
V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.9	…	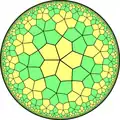V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	…	V3.3.5.3.5	…

Physikalische Ergänzung: Quasikristalle

Aus der Physik ist die strikte Aussage bekannt, dass es zwar sechszählige Kristallstrukturen gibt, aber keine fünfzähligen. Deshalb war es eine Überraschung und wurde 2011 mit einem Nobelpreis ausgezeichnet, als Dan Shechtman und Mitarbeiter 1984 fünfzählige Reflexe entdeckten, die sogenannten Quasikristallen zugeordnet sind, einer regelmäßig-unregelmäßigen Anordnung inkommensurabler Einheiten (Näheres bei den angegebenen Links).

Literatur

David Wells: The Penguin Dictionary of Curious and Interesting Geometry. Penguin Books, London 1991, ISBN 0-14-011813-6.
David Klarner: Mathematical Recreations: A Collection in Honor of Martin Gardner. Dover Publications, Mineola 1998, ISBN 0-486-40089-1.

Siehe auch

Penrose-Parkettierung

Weblinks

Commons: Parkettierung mit Fünfecken – Sammlung von Bildern, Videos und Audiodateien

Parkettierung mit Fünfecken.
Eric W. Weisstein: Pentagon Tiling. In: MathWorld (englisch).
The 14 Different Types of Convex Pentagons that Tile the Plane. (englisch).
Tilings with a convex pentagonal tile. (englisch).

Quellen

Karl Reinhardt: Über die Zerlegung der Ebene in Polygone. Inaugural-Dissertation, zur Erlangung der Doktorwürde der Hohen Naturwissenschaftlichen Fakultät der Königlichen Universität zu Frankfurt am Main, Robert Noske, Borna-Leipzig (1918). Bitte beachten: Auf S. 77 befindet sich ein Fehler. Die Winkelsumme γ + δ für die ersten beiden Parkettierungstypen muss π sein, und nicht 2π (wie angegeben).
Eyder Peralta: With Discovery, 3 Scientists Chip Away At An Unsolvable Math Problem. Bei: NPR.org. 14. August 2015, abgerufen am 21. August 2015.
M. D. Hirschhorn und D. C. Hunt: Equilateral convex pentagons which tile the plane. In: Journal of Combinatorial Theory. Series A, Band 39 (1), Mai 1985, S. 1–18.
Olga Bagina: Мозаики из выпуклых пятиугольников. (Tilings of the plane with convex pentagons.) Vestnik (russ.) (2011), Band 4 (48), S. 63–73, ISSN 2078-1768.
Olga Bagina: Tiling the plane with congruent equilateral convex pentagons. In: Journal of Combinatorial Theory. 2004, Band 105 (2), S. 221–232.
Teruhisa Sugimoto: Convex pentagons for edge-to-edge tiling, I. Forma, Band 27 (1) (2012), S. 93–103.
Richard Kershner: On paving the plane. In: American Mathematical Monthly. Band 75, S. 839–844.
George E. Martin: Transformation Geometry: An Introduction to Symmetry. Springer Science & Business Media, 1982, ISBN 978-0-387-90636-2, S. 126 (google.com).
M. Gardner: On Tessellating The Plane With Convex Polygon Tiles. In: Scientific American. Band 233 (1), S. 112–117, Munn & Company (1975).
Doris Schattschneider: Tiling the Plane with Congruent Pentagons. In: Mathematics Magazine. Band 51 (1), S. 29–44 (1978).
Alex Bellos: Attack on the pentagon results in discovery of new mathematical tile. In: TheGuardian.com, 11. August 2015, abgerufen am 10. September 2015.
Doris Schattschneider: A new pentagon tiler. In: Mathematics Magazine. Band 58 (5), S. 308 (1985). Diese neue Fünfeck-Parkettierung zierte auch die Vorderseite des Mathematics Magazine.
Michele Emmer, Doris Schattschneider: M.C. Escher’s Legacy: A Centennial Celebration. Springer, 2007, ISBN 978-3-540-28849-7, S. 244–251 (google.com).
Roses von Marjorie Rice.
Fishes von Marjorie Rice.
Butterflies von Marjorie Rice.
Ivars Peterson: Tiling with Pentagons. In: The Mathematical Tourist. 5. Juni 2010, abgerufen am 14. September 2015.
Derrick Niederman: Number Freak: From 1 to 200 – The Hidden Language of Numbers Revealed. Penguin Publishing Group, 2009, ISBN 978-1-101-13548-8, S. 83 (google.com).
Robert Gast: Das magische Pentagon. In: Sueddeutsche.de, 12. August 2015, abgerufen am 14. September 2015.
Eyder Peralta: With Discovery, 3 Scientists Chip Away At An Unsolvable Math Problem. In: NPR.org. 14. August 2015, abgerufen am 11. September 2015.
Casey Mann: 15th Pentagon. In: reddit.com, 1. August 2015, abgerufen am 14. September 2015.
Pentagon Tiling Proof Solves Century-Old Math Problem. Bei: quantamagazine.org. 11. Juli 2017, abgerufen am 13. Juli 2017.
100 Jahre altes Matherätsel. Das Ende der Fünfeck-Saga. Bei: spektrum.de. 13. Juli 2017, abgerufen am 13. Juli 2017.
Bei 6 der 7 Klassen dieser seiner hier wörtlich zitierten »Einteilung der Fünfecke« auf S. 76 verwendet Reinhardt tatsächlich das Wort »verschieden«. Gemeint ist aber zweifellos »möglicherweise verschieden«, also bei R-I: »die Seitenverhältnisse sind beliebig«.
Jaap Scherphuis © 2009–2017 Tilings
Tilings with a convex pentagonal tile k-isohedral (k∈{1,2,3,4}) eingefärbte Parkettierungen mit Fünfecken
Doris Schattschneider: Tiling the Plane with Congruent Pentagons. In: Mathematics Magazine. 1978, Fig. 12.
Bernhard Klaassen: Rotationally symmetric tilings with convex pentagons and hexagons. In: Elemente der Mathematik. Band 71, Nr. 4, 2016, ISSN 0013-6018, S. 137–144, doi:10.4171/em/310 (ems-ph.org).
Bernhard Klaassen: Rotationally Symmetric Tilings with Convex Pentagons and Hexagons. In: arXiv [math]. 2016, arxiv:1509.06297.
Chaim Goodman-Strauss: Tessellations. (PDF) Abgerufen am 24. April 2021.
M. und A. Rollett: Mathematical Models. Tarquin Pub., Stradbroke (England) 1952 (3. Ausgabe 1989), 3.7 The Archimedean Polyhedra. S. 101–115 und S. 118–119, Tabelle I, Nets of Archimedean Duals. V.a.b.c… as vertically-regular symbols.

Kommentare

Dreiecke mit geraden Linien sind immer konvex.
Die Geschlossenheit des gleichseitigen Polygonzugs erfordert:
cos(B) – cos(B+C) + cos(B+C+D) + cos(A) = 1 und

sin(B) – sin(B+C) + sin(B+C+D) – sin(A) = 0.
Daraus ergibt sich nach den Einsetzungen B = 360° – 2E, D = 360° – 2C, A = –180° + E + C zunächst –sin(C) = 2sin(E)/(1–2cos(E)) und schließlich für x := 2cos(E)
x⁴ – 10x² + 2x + 19 = 0.
Erklärungen zu der Tabelle:
- Die erste Zeile bezeichnet den Typ des Fünfecks („Kacheltyp“).
- Die zweite Zeile bezeichnet die ebene kristallographische Gruppe (oder Ornamentgruppe) einer Parkettierung der Ebene mit diesem Typ. Es kann aber weitere Parkettierungen geben, die hiervon abweichen.
- Die dritte Zeile zeigt eine Parkettierung mit diesem Fünfeck-Typ.
- Die vierte Zeile charakterisiert ein Fünfeck des zu definierenden Typs durch lineare Gleichungen von Seitenverhältnissen resp. von Winkeln: Alle Fünfecke, die die darunter stehenden Bedingungen erfüllen, gehören zum Typ. Die maximal sechs Bedingungen definieren keine Kongruenz, sondern höchstens Ähnlichkeit. Sind es weniger als sechs unabhängige Bedingungen, dann gehören auch unähnliche Fünfecke zum selben Typ.
- Die fünfte Zeile zeigt ein aus mehreren Fünfecken des Kacheltyps zusammengesetztes Kachelmuster, aus dem sich eine der gezeigten Parkettierungen ausschließlich durch Translationen herstellen lässt.
- Die letzte Zeile nennt ggf. den/die Entdecker des Typs.
Diese zweite Beziehung ist wegen der Gesamtwinkelsumme von 540° eine unmittelbare Folge der ersten. Im Ergebnis lässt dieser Typ fünf Freiheitsgrade, bspw. drei Winkel und zwei Seitenverhältnisse.
Dann ist E+2D=E+540°-2C=E+540°+B-360°=360°. Also sind die Bedingungen invariant gegen Spiegelung an der Ad-Achse.
ja = nur Kante-an-Kante; nein = es gibt keine Parkettierung Kante-an-Kante; beides = es gibt beides
nein = es gibt nur konvexe Parkettierungen
In Englisch Cairo tiling; diese Art der Pflasterung trägt diesen Namen seit 1971 und kann tatsächlich an mehreren Orten in Kairo gefunden werden, wie auf David Bailey’s World of Escher-like Tessellations (Memento des Originals vom 2. Oktober 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 dokumentiert wird.
Die Benennung nimmt Bezug auf das Muster, das wie eine 6-blättrige Blüte aussieht.
Es erfüllt die Bedingungen:
a=b=c=d=e und

2A+E = B+C+2D = B+C+E = 360°,
Bedingungen, die keinen Freiheitsgrad lassen und es in den konvexen Typ 2 einordnen. Aus ihnen folgt zunächst E = 2D, A = 180°–D, C = 360°–B–2D, B = 180°–3D und wegen der Geschlossenheit des Polygonzugs cos(3D)+cos(2D)+1 = 0, woraus man 4cos²(D)+2cos(D)–3 = 0, also D = cos⁻¹(^√13–1⁄₄) ≈ 49,35368° ausrechnet.
Diese geometrischen Formen, die aus kleineren Formen ihrer selbst zusammengesetzt sind, werden – eingeführt durch Solomon W. Golomb (Replicating Figures in the Plane. In: The Mathematical Gazette. Band 48, Nr. 366 (1964), S. 403–412) – im Englischen rep-tile oder reptile genannt, ein Wortspiel mit dem Begriff repetitive tile ‚sich wiederholende Kachel‘.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[KRDiss-2] Karl Reinhardt: Über die Zerlegung der Ebene in Polygone. Inaugural-Dissertation, zur Erlangung der Doktorwürde der Hohen Naturwissenschaftlichen Fakultät der Königlichen Universität zu Frankfurt am Main, Robert Noske, Borna-Leipzig (1918). Bitte beachten: Auf S. 77 befindet sich ein Fehler. Die Winkelsumme γ + δ für die ersten beiden Parkettierungstypen muss π sein, und nicht 2π (wie angegeben).

[NPR-3] Eyder Peralta: With Discovery, 3 Scientists Chip Away At An Unsolvable Math Problem. Bei: NPR.org. 14. August 2015, abgerufen am 21. August 2015.

[HuH-5] M. D. Hirschhorn und D. C. Hunt: Equilateral convex pentagons which tile the plane. In: Journal of Combinatorial Theory. Series A, Band 39 (1), Mai 1985, S. 1–18.

[OB-6] Olga Bagina: Мозаики из выпуклых пятиугольников. (Tilings of the plane with convex pentagons.) Vestnik (russ.) (2011), Band 4 (48), S. 63–73, ISSN 2078-1768.

[7] Olga Bagina: Tiling the plane with congruent equilateral convex pentagons. In: Journal of Combinatorial Theory. 2004, Band 105 (2), S. 221–232.

[8] Teruhisa Sugimoto: Convex pentagons for edge-to-edge tiling, I. Forma, Band 27 (1) (2012), S. 93–103.

[12] Richard Kershner: On paving the plane. In: American Mathematical Monthly. Band 75, S. 839–844.

[13] George E. Martin: Transformation Geometry: An Introduction to Symmetry. Springer Science & Business Media, 1982, ISBN 978-0-387-90636-2, S. 126 (google.com).

[14] M. Gardner: On Tessellating The Plane With Convex Polygon Tiles. In: Scientific American. Band 233 (1), S. 112–117, Munn & Company (1975).

[DS1978-15] Doris Schattschneider: Tiling the Plane with Congruent Pentagons. In: Mathematics Magazine. Band 51 (1), S. 29–44 (1978).

[AlexBellos-16] Alex Bellos: Attack on the pentagon results in discovery of new mathematical tile. In: TheGuardian.com, 11. August 2015, abgerufen am 10. September 2015.

[Schattschneider1985-17] Doris Schattschneider: A new pentagon tiler. In: Mathematics Magazine. Band 58 (5), S. 308 (1985). Diese neue Fünfeck-Parkettierung zierte auch die Vorderseite des Mathematics Magazine.

[EmmerSchattschneider2007-18] Michele Emmer, Doris Schattschneider: M.C. Escher’s Legacy: A Centennial Celebration. Springer, 2007, ISBN 978-3-540-28849-7, S. 244–251 (google.com).

[19] Roses von Marjorie Rice.

[20] Fishes von Marjorie Rice.

[21] Butterflies von Marjorie Rice.

[22] Ivars Peterson: Tiling with Pentagons. In: The Mathematical Tourist. 5. Juni 2010, abgerufen am 14. September 2015.

[23] Derrick Niederman: Number Freak: From 1 to 200 – The Hidden Language of Numbers Revealed. Penguin Publishing Group, 2009, ISBN 978-1-101-13548-8, S. 83 (google.com).

[24] Robert Gast: Das magische Pentagon. In: Sueddeutsche.de, 12. August 2015, abgerufen am 14. September 2015.

[25] Eyder Peralta: With Discovery, 3 Scientists Chip Away At An Unsolvable Math Problem. In: NPR.org. 14. August 2015, abgerufen am 11. September 2015.

[26] Casey Mann: 15th Pentagon. In: reddit.com, 1. August 2015, abgerufen am 14. September 2015.

[27] Pentagon Tiling Proof Solves Century-Old Math Problem. Bei: quantamagazine.org. 11. Juli 2017, abgerufen am 13. Juli 2017.

[28] 100 Jahre altes Matherätsel. Das Ende der Fünfeck-Saga. Bei: spektrum.de. 13. Juli 2017, abgerufen am 13. Juli 2017.

[29] Bei 6 der 7 Klassen dieser seiner hier wörtlich zitierten »Einteilung der Fünfecke« auf S. 76 verwendet Reinhardt tatsächlich das Wort »verschieden«. Gemeint ist aber zweifellos »möglicherweise verschieden«, also bei R-I: »die Seitenverhältnisse sind beliebig«.

[30] Jaap Scherphuis © 2009–2017 Tilings

[32] Tilings with a convex pentagonal tile k-isohedral (k∈{1,2,3,4}) eingefärbte Parkettierungen mit Fünfecken

[34] Doris Schattschneider: Tiling the Plane with Congruent Pentagons. In: Mathematics Magazine. 1978, Fig. 12.

[35] Bernhard Klaassen: Rotationally symmetric tilings with convex pentagons and hexagons. In: Elemente der Mathematik. Band 71, Nr. 4, 2016, ISSN 0013-6018, S. 137–144, doi:10.4171/em/310 (ems-ph.org).

[36] Bernhard Klaassen: Rotationally Symmetric Tilings with Convex Pentagons and Hexagons. In: arXiv [math]. 2016, arxiv:1509.06297.

[Chaim_Goodman-Strauss-40] Chaim Goodman-Strauss: Tessellations. (PDF) Abgerufen am 24. April 2021.

[42] M. und A. Rollett: Mathematical Models. Tarquin Pub., Stradbroke (England) 1952 (3. Ausgabe 1989), 3.7 The Archimedean Polyhedra. S. 101–115 und S. 118–119, Tabelle I, Nets of Archimedean Duals. V.a.b.c… as vertically-regular symbols.

[1] Dreiecke mit geraden Linien sind immer konvex.

[4] Die Geschlossenheit des gleichseitigen Polygonzugs erfordert:
cos(B) – cos(B+C) + cos(B+C+D) + cos(A) = 1 und

sin(B) – sin(B+C) + sin(B+C+D) – sin(A) = 0.
Daraus ergibt sich nach den Einsetzungen B = 360° – 2E, D = 360° – 2C, A = –180° + E + C zunächst –sin(C) = 2sin(E)/(1–2cos(E)) und schließlich für x := 2cos(E)
x⁴ – 10x² + 2x + 19 = 0.

[Haupttabelle-9] Erklärungen zu der Tabelle:
Die erste Zeile bezeichnet den Typ des Fünfecks („Kacheltyp“).

Die zweite Zeile bezeichnet die ebene kristallographische Gruppe (oder Ornamentgruppe) einer Parkettierung der Ebene mit diesem Typ. Es kann aber weitere Parkettierungen geben, die hiervon abweichen.

Die dritte Zeile zeigt eine Parkettierung mit diesem Fünfeck-Typ.

Die vierte Zeile charakterisiert ein Fünfeck des zu definierenden Typs durch lineare Gleichungen von Seitenverhältnissen resp. von Winkeln: Alle Fünfecke, die die darunter stehenden Bedingungen erfüllen, gehören zum Typ. Die maximal sechs Bedingungen definieren keine Kongruenz, sondern höchstens Ähnlichkeit. Sind es weniger als sechs unabhängige Bedingungen, dann gehören auch unähnliche Fünfecke zum selben Typ.

Die fünfte Zeile zeigt ein aus mehreren Fünfecken des Kacheltyps zusammengesetztes Kachelmuster, aus dem sich eine der gezeigten Parkettierungen ausschließlich durch Translationen herstellen lässt.

Die letzte Zeile nennt ggf. den/die Entdecker des Typs.

[35] Die erste Zeile bezeichnet den Typ des Fünfecks („Kacheltyp“).

[36] Die zweite Zeile bezeichnet die ebene kristallographische Gruppe (oder Ornamentgruppe) einer Parkettierung der Ebene mit diesem Typ. Es kann aber weitere Parkettierungen geben, die hiervon abweichen.

[37] Die dritte Zeile zeigt eine Parkettierung mit diesem Fünfeck-Typ.

[38] Die vierte Zeile charakterisiert ein Fünfeck des zu definierenden Typs durch lineare Gleichungen von Seitenverhältnissen resp. von Winkeln: Alle Fünfecke, die die darunter stehenden Bedingungen erfüllen, gehören zum Typ. Die maximal sechs Bedingungen definieren keine Kongruenz, sondern höchstens Ähnlichkeit. Sind es weniger als sechs unabhängige Bedingungen, dann gehören auch unähnliche Fünfecke zum selben Typ.

[39] Die fünfte Zeile zeigt ein aus mehreren Fünfecken des Kacheltyps zusammengesetztes Kachelmuster, aus dem sich eine der gezeigten Parkettierungen ausschließlich durch Translationen herstellen lässt.

[40] Die letzte Zeile nennt ggf. den/die Entdecker des Typs.

[10] Diese zweite Beziehung ist wegen der Gesamtwinkelsumme von 540° eine unmittelbare Folge der ersten. Im Ergebnis lässt dieser Typ fünf Freiheitsgrade, bspw. drei Winkel und zwei Seitenverhältnisse.

[11] Dann ist E+2D=E+540°-2C=E+540°+B-360°=360°. Also sind die Bedingungen invariant gegen Spiegelung an der Ad-Achse.

[31] = nur Kante-an-Kante; nein = es gibt keine Parkettierung Kante-an-Kante; beides = es gibt beides

[33] = es gibt nur konvexe Parkettierungen

[37] In Englisch Cairo tiling; diese Art der Pflasterung trägt diesen Namen seit 1971 und kann tatsächlich an mehreren Orten in Kairo gefunden werden, wie auf David Bailey’s World of Escher-like Tessellations (Memento des Originals vom 2. Oktober 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 dokumentiert wird.

[38] Die Benennung nimmt Bezug auf das Muster, das wie eine 6-blättrige Blüte aussieht.

[39] Es erfüllt die Bedingungen:
a=b=c=d=e und

2A+E = B+C+2D = B+C+E = 360°,
Bedingungen, die keinen Freiheitsgrad lassen und es in den konvexen Typ 2 einordnen. Aus ihnen folgt zunächst E = 2D, A = 180°–D, C = 360°–B–2D, B = 180°–3D und wegen der Geschlossenheit des Polygonzugs cos(3D)+cos(2D)+1 = 0, woraus man 4cos²(D)+2cos(D)–3 = 0, also D = cos⁻¹(^√13–1⁄₄) ≈ 49,35368° ausrechnet.

[41] Diese geometrischen Formen, die aus kleineren Formen ihrer selbst zusammengesetzt sind, werden – eingeführt durch Solomon W. Golomb (Replicating Figures in the Plane. In: The Mathematical Gazette. Band 48, Nr. 366 (1964), S. 403–412) – im Englischen rep-tile oder reptile genannt, ein Wortspiel mit dem Begriff repetitive tile ‚sich wiederholende Kachel‘.