Winkelsumme

Mit der (Innen-)Winkelsumme einer ebenen geometrischen Figur ist meistens die Summe aller Innenwinkel der Figur gemeint.

Beispiele und deren Winkelsummen

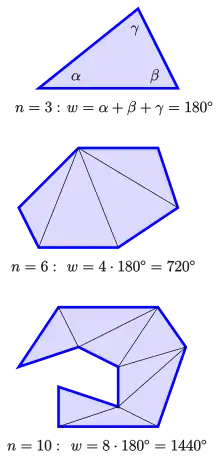
Winkelsumme in der euklidischen Geometrie

Für ein nicht-überschlagendes Polygon in der euklidischen Ebene ist seine Winkelsumme durch die Formel

(n\cdot 180^{\circ })-360^{\circ }=(n-2)\cdot 180^{\circ }

gegeben, wobei $n$ für die Zahl der Ecken des Polygons steht.

Beispiele

Aus der Formel ergeben sich für die Werte der Winkelsummen für Drei-, Vier- und Fünfecke:

für Dreiecke ( $n=3$ ): $(n-2)\cdot 180^{\circ }=(3-2)\cdot 180^{\circ }=180^{\circ }$
für Vierecke ( $n=4$ ): $(n-2)\cdot 180^{\circ }=(4-2)\cdot 180^{\circ }=360^{\circ }$
für Fünfecke ( $n=5$ ): $(n-2)\cdot 180^{\circ }=(5-2)\cdot 180^{\circ }=540^{\circ }$

Dreiecke

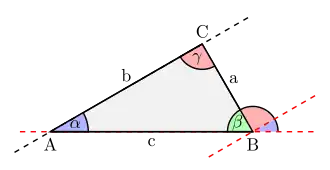
Zum Beweis der Winkelsumme im Dreieck:
Die beiden blauen Winkel sind gleich groß, da es sich um Stufenwinkel an Parallelen handelt, die beiden roten weil sie Wechselwinkel an Parallelen sind. Da alle drei Winkel an B den gestreckten Winkel bilden gilt:

\alpha +\beta +\gamma =180^{\circ }

Dass die Summe der Innenwinkel im Dreieck 180° ist, folgt aus den Axiomen der euklidischen Geometrie (siehe Grafik).[1] Die Winkelsumme im Dreieck ist als Lehrsatz mit Beweis in den Elementen des Euklid überliefert, der Mathematikhistoriker Thomas Heath hält es aber für möglich, dass sie bereits Thales von Milet bekannt war, wie es auch Moritz Cantor annahm.[2]

Allgemein

Man kann ein konvexes $n$ -Eck mit Hilfe eines Punktes im Innern in $n$ Teildreiecke teilen, die dann insgesamt eine Winkelsumme von $n\cdot 180^{\circ }$ haben. Allerdings muss man hiervon noch den Vollwinkel um diesen Punkt abziehen, also

n\cdot 180^{\circ }-360^{\circ }=n\cdot 180^{\circ }-2\cdot 180^{\circ }=\mathbf {(n-2)\cdot 180^{\circ }} .

Alternativ kann man sagen, dass von einer Ecke aus $(n-3)$ Diagonalen ausgehen, die das Polygon in $(n-2)$ Teildreiecke teilen, deren Winkelsumme also $(n-2)\cdot 180^{\circ }$ ist. Damit ist die Formel gezeigt.[3]

Für ein nicht-konvexes Polygon funktioniert dieser Ansatz allerdings nicht.

Für ein nicht-überschlagenes n-Eck (einfaches Polygon) ist es aber dennoch immer möglich, es so in n-2 Dreiecke aufzuteilen, dass deren gesamte Winkelsumme der Summe der Innenwinkel des Polygons entspricht.[4] Denn jedes nicht-überschlagene n-Eck lässt sich in Dreiecke zerlegen (siehe erstes Bild). Solch eine Zerlegung besteht immer aus n-2 Dreiecken[5]. Jeder Innenwinkel ist also entweder ein Dreieckswinkel oder Summe von solchen. Summiert man alle Innenwinkel auf, tritt jeder Dreieckswinkel genau einmal auf. Also gilt auch hier die obige Formel.

Winkelsumme in der nichteuklidischen Geometrie

In einer nichteuklidischen Ebene mit positiver Krümmung, beispielsweise auf der Oberfläche einer Kugel, beträgt die Winkelsumme stets mehr als die angegebenen Werte. Je größer das Polygon, desto größer ist im Allgemeinen die Abweichung. Beispiel: Auf der Erde hat das Dreieck, das vom Äquator, vom Nullmeridian und vom 90. Längengrad gebildet wird, die Winkelsumme 270°.

In einer nichteuklidischen Ebene mit negativer Krümmung, zum Beispiel auf einer Sattelfläche, beträgt die Winkelsumme stets weniger als die angegebenen Werte. Sie kann sogar Werte annehmen, die beliebig nahe bei 0 liegen.

Literatur

Roselyn Berman, Martin Berman: Concave Polygons. In: The Mathematics Teacher, Band 56, Nr. 6 (1963) S. 403–406 (JSTOR)

Weblinks

Sum of interior angles of a polygon - Video der Khan Academy (Video, Englisch mit deutschen Untertiteln, 9:10 Min.)
Geometrie-Quiz - Die Winkelsumme eines 100-Ecks. Spiegel Online, 10. April 2008

Einzelnachweise

Übersetzung des Beweises aus Euklids "Elemente": I.32 auf I 31 (Memento vom 24. Juni 2013 im Internet Archive).
A History of Greek Mathematics: Volume 1. "From Thales to Euclid". Clarendon Press, Oxford, 1921 (Nachdruck Dover 2012), S. 134
https://www.cliffsnotes.com/study-guides/geometry/polygons/angle-sum-of-polygons (abgerufen 19. April 2021)
Arnfried Kemnitz: Mathematik zum Studienbeginn: Grundlagenwissen für alle technischen, mathematisch-naturwissenschaftlichen und wirtschaftswissenschaftlichen Studiengänge. Springer, 2010, ISBN 9783834812933, S. 132
Handbook of Discrete and Computational Geometry, Second Edition, Heausg. Csaba D. Toth, Joseph O'Rourke, Jacob E. Goodman, Verlag CRC Press, 2004, ISBN 1420035312, S., 586, Theorem 26.2.1 .

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Übersetzung des Beweises aus Euklids "Elemente": I.32 auf I 31 (Memento vom 24. Juni 2013 im Internet Archive).

[2] A History of Greek Mathematics: Volume 1. "From Thales to Euclid". Clarendon Press, Oxford, 1921 (Nachdruck Dover 2012), S. 134

[3] ttps://www.cliffsnotes.com/study-guides/geometry/polygons/angle-sum-of-polygons (abgerufen 19. April 2021)

[4] Arnfried Kemnitz: Mathematik zum Studienbeginn: Grundlagenwissen für alle technischen, mathematisch-naturwissenschaftlichen und wirtschaftswissenschaftlichen Studiengänge. Springer, 2010, ISBN 9783834812933, S. 132

[5] Handbook of Discrete and Computational Geometry, Second Edition, Heausg. Csaba D. Toth, Joseph O'Rourke, Jacob E. Goodman, Verlag CRC Press, 2004, ISBN 1420035312, S., 586, Theorem 26.2.1 .