Optischer Fluss
Der optische Fluss einer Bildsequenz ist das Vektorfeld der in die Bildebene projizierten Geschwindigkeit von sichtbaren Punkten des Objektraumes im Bezugssystem der Abbildungsoptik.
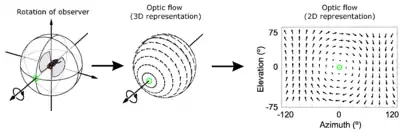

Der optische Fluss ist eine wichtige Repräsentation von Bewegungsinformation in frühen Stufen der Bildverarbeitung. Sie unterstützt, wie die Segmentierung nach Farben und Texturen, die Zuordnung von Punkten zu Objekten. Anwendungsbeispiele sind die optische Computermaus, die Bildstabilisierung von Kameras, die Motion Compensation in der Videokompression und die Sichtnavigation von Robotern und Tieren.
Als optischer Fluss wird auch das Ergebnis eines Algorithmus oder das eingesetzte Verfahren bezeichnet. Wichtige Methoden sind differentielle Verfahren, die in der Regel bildpunktweise arbeiten, und blockweise arbeitende Verfahren.
Methodik
Der lokale optische Fluss wird aus Mustern im Bild in einer mehr oder weniger großen Umgebung eines betrachteten Bildpunktes geschätzt. Aus dem lokalen Gradienten kann nur die zum Gradienten parallele Komponente des Flussvektors bestimmt werden. Dieses grundsätzliche Problem bezeichnet man als Aperturproblem.
Ob der interessierende Vektor genau bestimmt werden kann, hängt also davon ab, ob innerhalb des betrachteten Gebietes G Grauwert-Gradienten in unterschiedliche Richtungen vorliegen. Außerdem ist es notwendig, eine Modellvorstellung davon zu haben, welchen prinzipiellen Verlauf der optische Fluss innerhalb des betrachteten Gebietes haben kann. Im einfachsten Fall wird angenommen, dass der optische Fluss innerhalb kleiner Gebiete als konstant betrachtet werden kann. Kompliziertere Verläufe des Flussfeldes, z. B. affine Modelle, sind möglich und werden in leistungsfähigen Verfahren eingesetzt. Ein Interest-Operator liefert jene Punkte, deren Flussvektor besonders sicher bestimmt werden kann. In einigen Ansätzen wird nur an diesen ausgewählten Punkten der Fluss berechnet (feature point tracking).
Weitere Verfahren sind das kleinste-Quadrate-Matching und die Blockkorrelation (minimierte Summe der absoluten Differenzen, normalisierte Kreuzkorrelation). Eine Sonderform der blockweisen Bewegungsschätzung ist die auf der Fourier-Transformation aufbauende Phasenkorrelation (Inversion des normalisierten Kreuzleistungsdichtespektrums).
Der optische Fluss ist ein äußerst grundlegendes Konzept, das in der einen oder anderen Form in der Videoverarbeitung verwendet wird. Optische Flussmethoden basieren auf der Berechnung von Schätzungen der Bewegung der Bildintensitäten über die Zeit in einem Video. Die Strömungsfelder können dann analysiert werden, um Segmentierungen in Regionen zu erzeugen, die mit sich bewegenden Objekten verbunden sein können.
Es können Algorithmen verwendet werden, um unabhängig bewegte Objekte selbst bei Kamerabewegungen zu erkennen und abzugrenzen. Natürlich sind auf optischem Fluss basierende Techniken rechenintensiv und erfordern daher schnelle Hardware- und Softwarelösungen für die Implementierung. Da der optische Fluss grundsätzlich eine Differenzgröße ist, ist seine Schätzung sehr anfällig für Rauschen. Eine Verbesserung der Rauschempfindlichkeit kann zu einer Erhöhung der Komplexität führen. Daher müssen auf Smart-Kameras basierende Videoüberwachungssysteme, die Berechnungen des optischen Flusses verwenden, mit erheblichen Ressourcen ausgestattet sein, beispielsweise einem digitalen Signalprozessor, einem Field Programmable Gate Array oder einem anderen speziellen Beschleunigungsgerät. Videoüberwachungssysteme mit erheblichen intelligenten Fähigkeiten werden ins Auge gefasst und realisiert, weil solche Technologien in die Smart-Kamera-Technologie eingeführt werden.[1]
Differenzieller optischer Fluss
Die Berechnung des optischen Flusses mittels differenzieller Methoden geht auf das 1981 am Massachusetts Institute of Technology entwickelte Verfahren von Berthold Horn und Brian Schunck[2] zurück.
Man nimmt an, dass die Helligkeit an entsprechenden Stellen der Einzelbilder in der Bildsequenz konstant ist. Dann folgt aus der Ableitung
als notwendige Bedingung die Bestimmungsgleichung für die Geschwindigkeiten (siehe Kontinuitätsgleichung):
Die Lösung dieser Gleichung ist im Sinne von Jacques Hadamard ein schlecht gestelltes Problem. Daher wird von der Lösung zusätzlich Glattheit gefordert.
Es gibt mehrere Methoden, den optischen Fluss zu bestimmen, darunter:
- Lucas-Kanade-Methode
- Horn-Schunck-Methode
Einige bekannte Algorithmen zur Berechnung des optischen Flusses sind in der OpenCV-Bibliothek implementiert.
Anwendungen
- Objektverfolgung: wir Menschen können ein sich bewegendes Objekt einfach anhand seiner Bewegung erkennen. Auf diese Weise können wir ebenfalls verschiedene Objekte aufgrund ihrer unterschiedlichen Bewegung voneinander unterscheiden. Die Berechnung des optischen Fluss wird deswegen oft unterstützend eingesetzt, um zuerst ein bestimmtes Objekt zu identifizieren, und anschließend deren Bewegung innerhalb einer Bildsequenz zu verfolgen. Dabei wird angenommen, dass die Gradienten-Vektoren eines Objekts zwischen zwei Bildern in etwa gleich groß sind und innerhalb der Bildfolge sich gleichmäßig aber nicht sprunghaft ändern.
- Bildsegmentierung: genau wie bei der Objektverfolgung wird die Idee auch bei der Segmentierung eines Bildes eingesetzt. So lässt sich z. B. der unbewegte Hintergrund identifizieren oder verschiedene Bereiche mit ähnlichen Bewegungsmustern.
- Mobile Roboter: mit Kameras ausgerüstete mobile Roboter müssen in ihrer Umgebung navigieren, Hindernisse erkennen und umfahren. Dabei kommen Methoden zur Berechnung des optischen Flusses zum Einsatz zur Objektverfolgung und Bildsegmentierung.
- Videokompression: einige Verfahren zur Videokompression nutzen die Tatsache aus, dass sich aufeinander folgende Bilder kontinuierlich oder teilweise gar nicht verändern. Die Bewegung wird mittels optischem Fluss berechnet und gespeichert. Unbewegte Bildbereiche können damit entfallen und werden einfach vom letzten Einzelbild übernommen. Dadurch lässt sich die Größe des Videos reduzieren.
- Bewegungserfassung: der optische Fluss kommt auch bei Techniken zur Bewegungserfassung zum Einsatz. Dazu zählen z. B. die Erkennung von Gestik und Mimik oder die Erfassung komplexer Bewegungen einer ganzen Person zur realistischen Computeranimation bei Trickfilmen.
Optischer Fluss in der Natur
Bei Insekten
Bienen und andere Insekten mit Facettenaugen nutzen den optischen Fluss, um
- geradeaus zu fliegen: Die Drehrate wird so geregelt, dass Attraktor und Repeller des optischen Flusses einander diametral gegenüberliegen.
- Hindernissen auszuweichen: Die Flugrichtung wird in eine Richtung mit geringem optischen Fluss geändert.
- Abstände zu schätzen: Je größer bei gegebener Fluggeschwindigkeit das Maximum des optischen Flusses, desto geringer der Abstand. Fliegen können so an der Zimmerdecke landen, indem sie sich rechtzeitig in die Rückenlage drehen.
Physiologie beim Menschen
Ähnlich wie bei Insekten hilft uns der optische Fluss im Fußgänger- und Straßenverkehr: Wir nehmen die Bewegung der anderen Verkehrsteilnehmer aus den Augenwinkeln wahr und berücksichtigen sie unbewusst bei der eigenen Fortbewegung. So erkennen wir z. B. Objekte, die sich auf uns zu bewegen, an einem divergenten Fluss, d. h. das Vektorfeld strebt von einem Zentrum nach außen. Oder einfach gesagt: das Objekt wird größer.
Literatur
- Amar Mitiche, J. K. Aggarwal: Computer Vision Analysis of Image Motion by Variational Methods, Springer, Cham/Heidelberg/New York/Dordrecht/London 2014, ISBN 978-3-319-00711-3 (eBook)
Weblinks
- centeye.com: What is "Optical Flow"? (Memento vom 17. April 2010 im Internet Archive) (englisch)
- Optical Flow (englisch)
Einzelnachweise
- ScienceDirect: Optical Flow
- Berthold K. P. Horn, Brian G. Schunck: Determining optical flow. In: Artificial Intelligence. 17 (1-3), 1981, S. 185–203. doi:10.1016/0004-3702(81)90024-2.