Segmentierung (Bildverarbeitung)
Die Segmentierung ist ein Teilgebiet der digitalen Bildverarbeitung und des Computer-Sehens. Die Erzeugung von inhaltlich zusammenhängenden Regionen durch Zusammenfassung benachbarter Pixel oder Voxel entsprechend einem bestimmten Homogenitätskriterium bezeichnet man als Segmentierung.
Einordnung
Segmentierung ist im Prozess des maschinellen Sehens üblicherweise der erste Schritt der Bildanalyse und kommt nach der Bildvorverarbeitung. Der Ablauf ist also
Szene → Bildaufnahme → Bildvorverarbeitung → Segmentierung → Merkmalsextraktion → Klassifizierung → Aussage
Eigenschaften
Man spricht von einer vollständigen Segmentierung, wenn jedes Pixel mindestens einem Segment zugeordnet wird. Bei einer überdeckungsfreien Segmentierung wird jedes Pixel höchstens einem Segment zugeordnet. Bei einer vollständigen und überdeckungsfreien Segmentierung ist jedes Pixel also genau einem Segment zugeordnet. Eine Segmentierung nennt man zusammenhängend, wenn jedes Segment ein zusammenhängendes Gebiet bildet.
Verfahren
Es sind viele Verfahren zur automatischen Segmentierung bekannt. Grundsätzlich werden sie oft in pixel-, kanten- und regionenorientierte Verfahren eingeteilt. Zusätzlich unterscheidet man modellbasierte Verfahren, bei denen man von einer bestimmten Form der Objekte ausgeht, und texturbasierte Verfahren, bei denen auch eine innere homogene Struktur der Objekte berücksichtigt wird. Die Grenzen zwischen den Verfahren sind oft fließend. Auch kann man verschiedene Verfahren kombinieren, um bessere Ergebnisse zu erzielen.
Stattdessen kann man auch in einem manuellen Verfahren die Segmentierung ausführen, d. h., ein Mensch nimmt die Einteilung vor. Da die automatischen Verfahren weit von Perfektion entfernt sind, gibt es auch die Möglichkeit zur semi-automatischen Bearbeitung.
Pixelorientierte Verfahren
Pixelorientierte Verfahren treffen für jeden einzelnen Bildpunkt die Entscheidung, ob er zu einem bestimmten Segment gehört oder nicht. Diese Entscheidung kann – muss aber nicht – durch die Umgebung beeinflusst sein. Punktorientierte Verfahren sind meist einfach zu berechnen und deswegen schnell, liefern per se aber zunächst keine zusammenhängenden Segmente. Von Segmentierung spricht man, wenn auf einem binarisierten Bild einzelne Objekte abzählbar werden. Jedes segmentierte Objekt wird dann z. B. durch eine Lauflängencodierung der binarisierten Pixel beschrieben. Die Binarisierung ist die Vorstufe einer Segmentierung.
Das verbreitetste Binarisierungsverfahren ist sicherlich das Schwellwert-Verfahren. Dieses Verfahren beruht auf einem Schwellwert, der am besten über ein Histogramm bestimmt wird.
 Beispielbild |
 Bild nach Binarisierung mit Schwellwert 90 |
In der Abbildung ist der Hintergrund heller als das schwarze Objekt. Im einfachsten Fall ergibt sich der Schwellwert der Binarisierung aus dem Mittelwert von dunkelstem und hellstem Grauwert im Bild. Die Segmentierung ist häufig die Vorstufe einer Klassifikation.
Kantenorientierte Verfahren
In diesen Verfahren wird im Bild nach Kanten oder Objektübergängen gesucht. Viele Algorithmen liefern noch keine geschlossenen Kantenzüge, diese müssen erst mit weiteren Verfahren zusammengefügt werden, damit sie Objekte einschließen. Eigentlich liegen Kanten immer zwischen den Pixelregionen eines Bildes. Die Ergebnisse eines Algorithmus können Polygone (bzw. Linien oder in besonderen Fällen Kurven) sein, aber manche Operationen liefern die Kanten auch als andersfarbige Pixel. Bei der Software OpenCV wird jedes segmentierte Objekt durch einen umschließenden Polygonzug beschrieben. Eine Segmentierung kann auch dazu dienen, ein Bild in eine Vordergrundebene und eine Hintergrundebene einzuteilen.
Mit Verfahren wie dem Sobel-Operator und dem Laplace-Operator, sowie einer Gradientensuche lassen sich zu einer Kante gehörige Pixel finden. Diese sind aber in der Regel zunächst noch lose und müssen mit Kantenverfolgungsalgorithmen komplettiert werden. Ein populäres Verfahren zur Erzeugung einer zusammenhängenden Objektsilhouette oder zumindest von Kantenzügen aus den Kantenpixeln ist das Live-Wire-Verfahren von E. Mortensen, W. A. Barrett und J. K. Udupa. Die Idee kann anschaulich gesprochen mit einem Navigationssystem verglichen werden, welches einen optimalen Weg vom Start- zum Zielort ermittelt. Optimal bedeutet im Kontext der Segmentierung, dass der Weg zwischen Start und Ziel immer über die stärksten Kantenpixel führt. Die Wahl eines optimalen Weges ist ein Standardproblem der Informatik und kann beispielsweise mit einer Breitensuche gelöst werden.
Es gibt immer eine Kante zwischen zwei benachbarten Regionen mit verschiedenen Graustufenwerten. Die Kanten können als diskontinuierliche (unterbrochene) lokale Merkmale eines Bildes betrachtet werden. Diese Diskontinuität kann man verwenden, um Kanten zu erkennen und somit eine Grenze des Objekts zu definieren. Dies hilft bei der Erkennung der Formen mehrerer Objekte, die in einem bestimmten Bild vorhanden sind. Das geschieht in mehreren Schritten:
- Es wird eine Faltungsmatrix (auch Filterkern genannt) definiert
- Der Filter wird oben auf das Bild gelegt
- Die elementweise Multiplikation wird ausgeführt
- Die Faltungsmatrix wird pro ausgewähltem Schritt verschoben
- Faltungen durchführen, bis alle Pixel der Eingabe verwendet wurden
Die Werte der Faltungsmatrix definieren die Ausgabe der Faltung. Eine solche Faltungsmatrix ist der Sobel-Operator, der typischerweise zur Erkennung von Kanten verwendet wird. Der Sobel-Operator hat zwei Faltungsmatrizen – eine zum Erfassen der horizontalen Kanten und eine andere zum Erfassen der vertikalen Kanten. Die Kantenerkennung funktioniert, indem diese Filter über das angegebene Bild übertragen werden.[1]
Ein ebenfalls sehr bekanntes Verfahren ist die Wasserscheidentransformation, die auf Graustufenbildern arbeitet und immer geschlossene Kantenzüge liefert. Weitere Verfahren sind parallele und sequentielle Kantenextraktion, optimale Kantensuche, der Felzenszwalb-Huttenlocher-Algorithmus, Active Shape Models und Snakes.
Regionenorientierte Verfahren
Eine einfache Möglichkeit, verschiedene Objekte zu segmentieren, besteht darin, ihre Pixelwerte zu verwenden. Die Pixelwerte unterscheiden sich für die Objekte und den Bildhintergrund, wenn ein scharfer Kontrast zwischen ihnen besteht. In diesem Fall kann ein Schwellenwert festlegelegt werden. Die Pixelwerte, die diesen Schwellenwert unter- oder überschreiten, können entsprechend als Objekt oder Hintergrund klassifiziert werden. Diese Technik wird als Schwellenwertsegmentierung bezeichnet. Wenn das Bild in zwei Bereiche (Objekt und Hintergrund) unterteilt werden soll, kann man einen einzigen Schwellenwert, den globalen Schwellenwert, definieren. Wenn es außer dem Hintergrund mehrere Objekte gibt, muss man mehrere Schwellenwerte definieren. Diese Schwellenwerte werden als lokale Schwellenwerte bezeichnet.
Wenn z. B. der Pixelwert über einem Schwellenwert liegt, und in diesem Beispiel das Objekt heller ist, als der Hintergrund, gehört das Pixel zu einem bestimmten Objekt. Wenn der Pixelwert kleiner als der Schwellenwert ist, wird er als Hintergrund behandelt, weil er dunkler ist, als das Objekt. Die Zuordnung was Objekt und was Hintergrund ist (hell oder dunkel?), hängt natürlich vom Bildinhalt ab. Die Vorteile dieser Methode sind, dass die Berechnungen einfach sind und schnell berechnet werden können. Wenn das Objekt und der Hintergrund einen hohen Kontrast aufweisen, funktioniert diese Methode sehr gut. Dieser Ansatz unterliegt jedoch einigen Einschränkungen. Wenn es keine signifikanten Graustufenunterschiede gibt oder die Helligkeitswerte verschiedener Objekte sich überlappen, wird es sehr schwierig, die Pixel den Objekten zuzuordnen.[1]
Die regionenorientierten Verfahren betrachten Punktmengen als Gesamtheit und versuchen dadurch zusammenhängende Objekte zu finden. Häufige Verwendung finden Verfahren wie Region Growing, Region-Splitting, Pyramid Linking und Split and Merge.
Mathematisch anspruchsvoller kann das Bild nicht als Matrix von Pixeln, sondern als stetige Funktion verstanden werden, die beispielsweise das Einheitsquadrat in den Farbraum abbildet (z. B.: für ein Graustufenbild).
Energiemethoden ordnen jeder möglichen Segmentierung des Bildes einen reellen Energiewert zu und suchen ein Minimum dieses Energiefunktionals. Dabei wird unter einer Segmentierung ein Bild mit Bereichen gleichförmiger (oft konstanter) Farbintensität verstanden, zwischen den Regionen trennt eine Menge . Es können je nach Anwendungsfeld verschiedene Energien verwendet werden. Meist gehen ein:
- Der Unterschied zwischen Segmentierung und Originalbild, z. B.
- Ein Maß für die Länge der Kanten zwischen einzelnen Segmentierungsbereichen, beispielsweise , das zweidimensionale Hausdorff-Maß als Länge der Segmentierungskante.
- Wenn die Segmentierungsbereiche keine konstante Intensität besitzen müssen: Ein Maß für Intensitätsunterschiede wie beispielsweise .
Mögliche Lösungsverfahren sind dann:
- Graph-Cut-Verfahren, die zwar vom kontinuierlichen Modell ausgehen, dennoch einen diskreten Algorithmus ergeben,
- Variationsmethoden, die einen Abstieg der Energiefunktion als Lösung einer partiellen Differentialgleichung erreichen.
Erstere sind derzeit für kleinere Bilder in Echtzeit (30 fps) durchführbar, bieten jedoch maximal Pixelgenauigkeit. Der Variationsansatz erlaubt hingegen auch Subpixelgenauigkeit. Diese ist insbesondere bei diagonalen Kanten ausgesprochen hilfreich, weil bei diskreten Verfahren stets Treppeneffekte erzeugt werde, die mit dem Variationsansatz vermieden werden. Es werden derzeit Methoden erforscht, die Variationsansätze auf den Prozessoren von Grafikkarten (Graphic Processing Unit, GPU) zu lösen. Es werden Geschwindigkeitsvorteile von einem Faktor 5 bis 40 vorausgesagt, womit die Variationsansätze erheblich schneller wären.
Kontinuierliche Methoden werden erst seit etwa 2002 mit sichtbarem Erfolg erforscht und sind deshalb in Endbenutzersoftware noch nicht zu finden.
Cluster-Verfahren


Der k-Means-Algorithmus ist eine iterative Technik, mit der ein Bild in k Cluster aufgeteilt wird. Der grundlegende Algorithmus hat folgende Schritte:
- Wähle k Cluster-Zentren, entweder zufällig oder basierend auf einer heuristischen Methode
- Weise jedes Pixel in dem Bild dem Cluster zu, der den Abstand zwischen dem Pixel und dem Clusterzentrum minimiert
- Berechnen die Cluster-Zentren erneut, indem alle Pixel im Cluster gemittelt werden
- Wiederhole die Schritte 2 und 3, bis die Konvergenz erreicht ist, d. h. keine Pixel das Cluster wechseln
In diesem Fall ist der Abstand die quadratische oder absolute Differenz zwischen einem Pixel und einem Clusterzentrum. Der Unterschied basiert typischerweise auf Pixelfarbe, Intensität, Textur und Ort oder einer gewichteten Kombination dieser Faktoren. k kann manuell, zufällig oder von einer Heuristik ausgewählt werden. Dieser Algorithmus konvergiert immer, gibt jedoch nicht immer die optimale Lösung zurück. Die Qualität der Lösung hängt von der initialen Menge von Clustern und dem Wert von k ab.
Modellbasierte Verfahren
Hierbei wird ein Modell der gesuchten Objekte zugrunde gelegt. Dies kann beispielsweise die Form betreffen. Man setzt also Wissen über das Bild mit ein. Ein bekanntes Verfahren ist die Hough-Transformation, mit deren Hilfe man Punkte zu Linien oder Kreisen zusammenfügen kann, indem man sie in einem Parameterraum abbildet. Es finden weiterhin statistische Modelle und Segmentierung über Templates (Template-Matching) Verwendung. Bei letzterem Verfahren wird im Bild nach gegebenen Vorlagen gesucht.
Texturorientierte Verfahren
Manche Bildobjekte besitzen keine einheitliche Farbe, sondern eine einheitliche Textur. Beispielsweise kann ein Objekt Rillen besitzen, die dann in der Fotografie als abwechselnde Streifen dunkler und heller Farbe erscheinen. Damit diese Objekte nicht in viele kleine Objekte anhand der Textur zerlegt werden, benutzt man Ansätze, mit denen man versucht, diesem Problem zu begegnen. Diese Verfahren sind teilweise im Grenzbereich zur Klassifikation oder erlauben gleichzeitige Segmentierung und Klassifizierung.
- Cooccurrence-Matrizen (Haralick-Matrizen)
- Texturenergiemaße (Texture-Energy-Measure)
- Lauflängenmatrizen (Run-Length-Matrix)
- fraktale Dimensionen und Maße
- Markow-Random-Fields und Gibbs-Potentiale
- strukturelle Ansätze
- signaltheoretische Konzepte
Probleme
Oftmals ist die Qualität einer Segmentierung nicht optimal. In diesen Fällen kann man ein besseres Verfahren wählen, oder man kann die Ergebnisse optimieren, indem man eine Vorbearbeitung (auch Preprocessing) oder eine Nachbearbeitung anschließt. Beides kann sowohl automatisch (wenn man die Probleme des Prozesses bereits identifiziert hat) als auch per Hand erfolgen.
Ein Problem vieler Segmentierungsalgorithmen ist die Anfälligkeit für wechselnde Beleuchtung innerhalb des Bildes. Dies kann dazu führen, dass immer nur ein Bildteil korrekt segmentiert wird, in den anderen Bildteilen die Segmentierung aber unbrauchbar ist. Helligkeitsunterschiede kann man mit einer Vorbearbeitung ausgleichen, zum Beispiel indem man eine Shading-Korrektur anwendet.
Häufige Probleme sind beispielsweise Übersegmentierung (zu viele Segmente) und Untersegmentierung (zu wenige Segmente). Dem kann man begegnen, indem man das Verfahren um Wissen der zu verarbeitenden Daten anreichert, im einfachsten Fall kann man die erwartete Anzahl der Segmente angeben. Außerdem kann man einen nachfolgenden Klassifikationsschritt einfügen, um gleich klassifizierte Segmente zusammenzufassen. Natürlich können die Segmente auch per Hand zusammengefasst werden.
Viele der vorgestellten Algorithmen (Schwellwertverfahren, Wasserscheidentransformation) arbeiten nur auf einkanaligen Graustufenbildern. Bei der Verarbeitung von Mehrkanalbildern (zum Beispiel Farbbildern) bleiben Informationen ungenutzt. Man benötigt weitere Bearbeitungsschritte, um mehrere einkanalige Segmentierungen zusammenzufassen.
Anwendungen
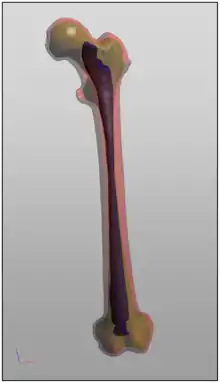
Segmentierung ist oft der erste Schritt der Bildanalyse für eine anschließende Weiterverarbeitung der Daten, beispielsweise eine Klassifizierung.
Die Anwendungen für solche Verfahren sind vielfältig. Am häufigsten werden derzeit automatische Segmentierungen in der Medizin angewandt, zum Beispiel in der Computertomographie oder in der Magnetresonanztomographie. Auch in der Geodatenverarbeitung werden Segmentierungen verwendet, beispielsweise werden Satellitenbilder oder Luftbilder (siehe Fernerkundung) zu geometrischen Daten segmentiert. Auch zur automatischen optischen Qualitätskontrolle von Werkstücken (zum Beispiel: Ist das Bohrloch an der richtigen Stelle?) wird Segmentierung verwendet. Ebenfalls wird Segmentierung in der Schrifterkennung (OCR) verwendet, um durch Binarisierung des gescannten Bildes Schrift vom Hintergrund zu trennen. Ein weiteres Thema ist die Gesichtserkennung.
Software
Bildverarbeitungsprogramme
Bildverarbeitungsprogramme wie das freie Scikit-image[2] bieten Segmentierungsalgorithmen und 'höhere' Bildverarbeitungsalgorithmen auf der Basis verschiedener Segmentierungsalgorithmen an. Mit diesen Programmen kann man zum Beispiel in einer Robotik-Anwendung Positionen von Objekten ermitteln (siehe Bildverarbeitung).
Bildbearbeitungsprogramme
Viele Bildbearbeitungsprogramme, wie das freie GIMP und das kostenlose IrfanView bieten einfache Segmentierungsalgorithmen an, wie etwa nach Schwellwertverfahren oder Kantendetektion mit Sobel- oder Laplace-Operatoren.
Schrifterkennung und Spezialsoftware
Schrifterkennungsprogramme können als ersten Schritt eine Segmentierung einsetzen, um die Schrift vom Hintergrund zu trennen.
Bei der Spezialsoftware zur Segmentierung von Bildern sind auch Medizin und Geoinformatik häufige Zieleinsatzgebiete.
Literatur
- Rafael C. Gonzalez, Richard E. Woods: Digital Image Processing. Addison-Wesley, Redding 1992, ISBN 0-201-50803-6. (englisch)
- Rainer Steinbrecher: Bildverarbeitung in der Praxis. Oldenbourg, München und Wien 1993, ISBN 3-486-22372-0.
- Thomas Bräunl, Stefan Feyrer, Wolfgang Rapf, Michael Reinhardt: Parallele Bildverarbeitung. Addison-Wesley, Bonn 1995, ISBN 3-89319-951-9.
- Thomas Lehmann, Walter Oberschelp, Erich Pelikan, Rudolf Repges: Bildverarbeitung für die Medizin. Springer, Berlin und Heidelberg 1997, ISBN 3-540-61458-3.
- Bernd Jähne: Digitale Bildverarbeitung. 5. Auflage. Springer, Berlin 2002, ISBN 3-540-41260-3.
Weblinks
- Verfolgung von farblich markierten Objekten (PDF; 400 kB)
Einzelnachweise
- Pulkit Sharma, Analytics Vidhya: Computer Vision Tutorial: A Step-by-Step Introduction to Image Segmentation Techniques (Part 1)
- scikit-image.org: Module: segmentation — skimage docs. Abgerufen am 8. September 2018 (englisch).