Kartennetzentwurf
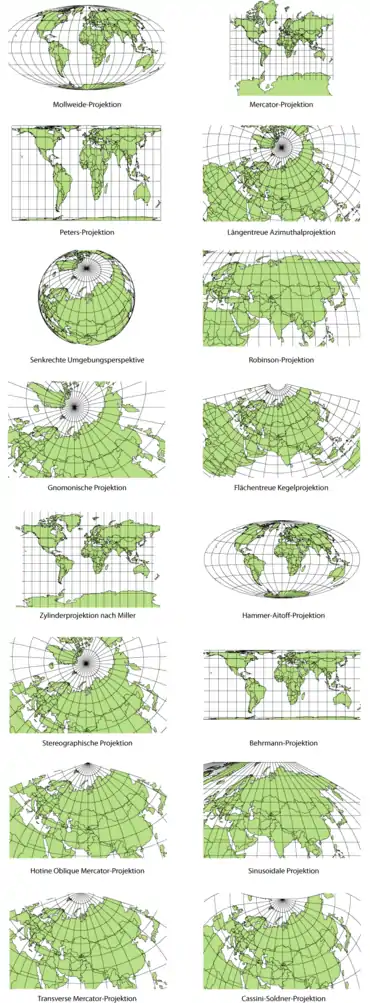
Ein Kartennetzentwurf (auch Kartenprojektion oder Kartenabbildung genannt) ist eine Methode in der Kartografie, mit der man die gekrümmte Oberfläche der (dreidimensionalen) Erde auf die flache (zweidimensionale) Karte überträgt.
Vorgehen
Der Prozess der Modellbildung geschieht mit Hilfe von Abbildungsvorschriften, die man mathematisch ausdrücken kann. Kartenprojektionen kann man auch anschaulich graphisch oder geometrisch erklären.
In der modernen Entwicklung hin zur Geodateninfrastruktur (Technologie und Terminologie) bilden Kartennetzentwürfe eine spezielle Gattung von Koordinatenreferenzsystemen und stellen dabei eine Konversionsmethode eines mathematischen Erdmodells in die Ebene dar. Es sind über 400 verschiedene Abbildungen bekannt.
Bei der Nutzung von Kartennetzentwürfen sind grundsätzlich drei Schritte notwendig:
- Auswahl eines geeigneten Modells (normalerweise wählt man zwischen einer Kugel und einem Ellipsoid) für die Form der Erde oder des abzubildenden Gegenstandes (beispielsweise anderer planetarischer Körper)
- Umwandlung der geographischen Koordinaten (Länge und Breite) in ein kartesisches Koordinatensystem (x und y oder Rechtswert und Hochwert)
- Skalierung der Karte (in der manuellen Kartografie kam dieser Schritt an zweiter Stelle, bei der digitalen Kartografie kann er zuletzt kommen)
Kategorien
Grundsätzlich klassifiziert man Kartennetzentwürfe entweder nach
- der Abbildungsfläche
- der Lage der Abbildungsfläche
- den Abbildungseigenschaften (Verzerrungseigenschaften)
- echten bzw. unechten (Pseudo)abbildungen.
Viele Netzentwürfe wurden nach ihren Erfindern benannt (siehe Liste von Kartennetzentwürfen)
Klassifikation nach Abbildungsflächen
Auswahl der Abbildungsfläche
Die meisten Kartennetzentwürfe sind keine Projektionen in physikalischer Hinsicht. Sie beruhen eher auf mathematischen Formeln. Um jedoch das Konzept der Kartenprojektion zu verstehen, ist es hilfreich, sich einen Globus mit einer Lichtquelle vorzustellen. Diese Lichtquelle projiziert die Punkte, Linien und Flächen des Globus auf eine Hilfsfläche, die sich einfach in die Ebene abrollen lässt.
Als Hilfsfläche kann man entweder eine Ebene, eine Kegel-, eine Zylinder- oder eine andere Fläche nutzen. Durch die Projektion der Globuselemente auf diese Hilfsfläche erhält man ein flaches Abbild. Allerdings muss man Kegel- und Zylinderfläche vorher noch in die Ebene abrollen. Grundsätzlich kann man alle Kartenprojektionen nach der Art der genutzten Hilfsfläche unterscheiden.
Schließlich ist es von Bedeutung, ob die Hilfsfläche modellhaft den Globus berührt oder schneidet. Bei einer zylindrischen Abbildung berührt (in normaler Lage) die Abbildungsfläche den Globus rund um den Äquator (an dieser Stelle gibt es auch keine Verzerrungen), ein Schnittzylinder schneidet dagegen den Globus an den nördlichen und südlichen Breitenkreisen. Das Prinzip gilt für alle Abbildungshilfsflächen.
| Hilfsfläche | Projektionsname | Beispiel |
|---|---|---|
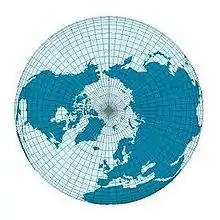
| Ebene | azimutale Abbildung Azimutalprojektion |
 |
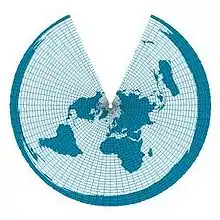
| Kegel | konische Abbildung Kegelprojektion |
 |
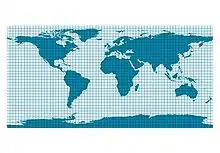
| Zylinder | zylindrische Abbildung Zylinderprojektion |
 |
Azimutale Abbildungen
Bei einer azimutalen Abbildung berührt die Bildebene die Erde an einem Punkt. Viele azimutale Abbildungen sind echte perspektivische Projektionen (Zentralprojektionen), das heißt, sie können auch geometrisch konstruiert werden.
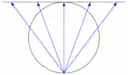 Stereografische Projektion
Stereografische Projektion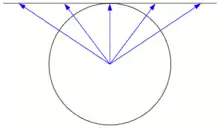 Gnomonische Projektion
Gnomonische Projektion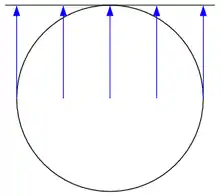 Orthografische Projektion (unendlich ferner Zentralpunkt)
Orthografische Projektion (unendlich ferner Zentralpunkt)
Der wahre Anblick der Erdkugel (oder eines anderen Himmelskörpers) ist kartographisch wenig geeignet, nicht nur ist er weder längen-, winkel- oder flächentreu, er zeigt auch nur einen begrenzten Ausschnitt einer Hemisphäre (der halben Oberfläche). Ein geostationärer Satellit beispielsweise hat eine Ausleuchtungszone von theoretisch maximal nur 42 % der Erdoberfläche, von über dem Pol aus sähe man den Äquator nicht. Folgende geometrische Projektionen mit einem Projektionszentrum sind üblich, um diesen Missstand zu beheben:
- Orthografische Azimutalprojektion, auch allgemein „Parallelprojektion“ genannt, bei der die Projektionsstrahlen parallel sind. Das Projektionszentrum liegt sozusagen im Unendlichen. Sie wird zur anschaulichen Darstellung der Erdkugel, sowie zur Darstellung anderer Himmelskörper (Mond, Planeten) verwendet.
- Stereografische Projektion (konforme azimutale Projektion), bei der das Projektionszentrum gegenüber dem Berührungspunkt liegt. Sie wird u. A. wegen der Winkeltreue für Sternkarten verwendet.
- Gnomonische Projektion, auch „Zentralprojektion“ genannt („zentral“ bezieht sich hier auf das Zentrum der Erde), bei der das Projektionszentrum im Erdmittelpunkt liegt. Sie bildet alle Großkreise als Geraden ab. Daher wird sie gerne in der Navigation verwendet, um die kürzeste Verbindung zwischen zwei Punkten zu finden.
 Mittabstandstreue Azimutalprojektion
Mittabstandstreue Azimutalprojektion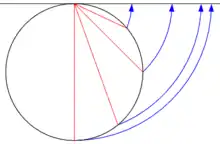 Lambertsche Azimutalprojektion
Lambertsche Azimutalprojektion
Weitere Abbildungen sind rein mathematisch definiert. Sie lassen sich in der Regel nicht mit Zirkel und Lineal geometrisch konstruieren. Dafür besitzen sie spezielle Eigenschaften, die von den geometrischen Projektionen nicht erreicht werden. Verwendung finden vor allem:
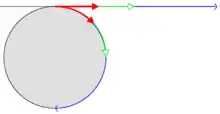
- Mittabstandstreue Azimutalprojektion (äquidistante azimutale Projektion), bei der die Abstände vom Kartenmittelpunkt unverzerrt wiedergegeben werden. Sie wird z. B. von Funkdiensten genutzt: Die Antenne steht im Berührungspunkt, und man kann so leicht die Himmelsrichtung und die Entfernung zu seinem Funkpartner ermitteln.
- Flächentreue Azimutalprojektion nach J.H. Lambert. Sie wird u. a. bei Atlaskarten verwendet.
Unter Unechte azimutale Abbildungen fasst man alle mathematischen Konstruktionen zusammen, die den echten Azimutalprojektionen ähneln.
Kegelabbildungen (konische Abbildungen)
Bei konischen Abbildungen (Kegelprojektionen) wird die Erde auf einen Kegel abgebildet. Die Kegelachse verläuft durch den Erdmittelpunkt. Die Lage der beiden Schnitt- oder des Berührkreises bestimmt Form und Lage des Kegels. Azimutale und zylindrische Abbildungen sind Grenzfälle der allgemeinen Kegelabbildung. Für Kegel in normaler Lage gilt:
- Öffnungswinkel → 180°: azimutale Abbildung
- Öffnungswinkel → 0°: zylindrische Abbildung
- Längentreue Kegelprojektion
- Lamberts winkeltreue Kegelprojektion
- Albers-Kegelprojektion (flächentreu)
Unechte Kegelabbildungen sind ebenfalls konoide Konstruktionen, wie die Herzform (Bonnesche Projektion, Stab-Wernersche Projektion).
Zylinderabbildungen
Zylinderprojektionen werden mit Hilfe eines Zylinders um die Erde konstruiert.
- längentreue Zylinderprojektion, rechteckige Plattkarte (Rektangularprojektion), und insbesondere die quadratische Plattkarte (geographische Projektion)
- Mercator-Projektion
- flächentreue Zylinderprojektion oder (Gall-)Peters-Projektion
- Miller-Zylinderprojektion
- Lamberts flächentreue Zylinderprojektion
Beim Gauß-Krüger- und beim UTM-Koordinatensystem werden transversale Zylinderprojektionen (liegende Zylinderachse) genutzt.
Unechte Zylinderabbildungen sind mathematisch konstruierte Abbildungen, bei denen der Mittelmeridian und alle Breitenkreise gerade oder zumindest gestreckte Linien sind.
Klassifikation nach Lage bzw. Aspekt der Abbildungsfläche
Nachdem die Wahl der Hilfsfläche feststeht, muss nun über ihre Lage entschieden werden. Zur Beschreibung nutzt man die Erdachse und die Masselinie des Hilfskörpers. Bei einer Ebene ist das die Senkrechte, bei einem Zylinder die Mittellinie und bei einem Kegel die Mittellinie durch die Spitze. Die unterschiedlichen Abbildungsflächen lassen sich an beliebigen Stellen an die Kugeloberfläche anlegen. Die Wahl der Lage (= Aspekt der Abbildungsfläche) wird durch den abzubildenden Teil der Erdoberfläche bestimmt, für den die Abbildung optimiert werden soll:
- normale Abbildungen
- transversale Abbildungen
- schiefachsige Abbildungen.
| Lage/Aspekt | Beschreibung | Beispiel |
|---|---|---|
| normal oder polständig | Achse der Hilfsfläche entspricht Erdachse |  |
| transversal oder querachsig, äquatorständig | Achse der Hilfsfläche liegt senkrecht zur Erdachse | 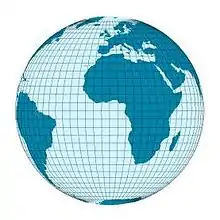 |
| schiefachsig oder schiefständig | Achse der Hilfsfläche liegt schief zur Erdachse | 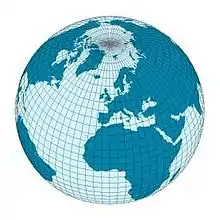 |
Klassifikation nach Abbildungseigenschaften (Verzerrungseigenschaften)
Eine Karte sollte möglichst exakt das Original wiedergeben. Bei der Abbildung der Kugel auf die Ebene sind allerdings Verzerrungen unvermeidlich. (Mathematisch: Die Gaußsche Krümmung ist eine Invariante unter Isometrien; die Kugelfläche mit Radius r besitzt die Krümmung 1/r², die Ebene hingegen die Krümmung 0, folglich kann es keine Isometrie zwischen Kugelfläche und Ebene geben.) Dieses Phänomen kann man sich mit Hilfe einer Orange vorstellen: Selbst wenn man es schafft, diese in einem Stück zu schälen, kann man die Schale (Erdoberfläche) nur mit starkem Drücken flach bekommen (Papier) und nimmt dabei Verzerrungen in Kauf (die Schale dehnt sich, reißt oder faltet sich). Dieses Phänomen der Verzerrung lässt sich differenzialgeometrisch begründen. Zur Beschreibung der lokalen Verzerrungseigenschaften in einem Punkt wird die Tissotsche Indikatrix (Verzerrungsellipse) verwendet.
Somit können sich die Länge einer Strecke, die Größe und Form einer Fläche oder der Winkel zwischen zwei Linien durch die Kartenprojektion verändern. Demzufolge kann auch der Maßstab auf einer Karte variieren. Ein populäres Beispiel ist die nahezu riesige Darstellung von Grönland bei der Mercatorprojektion. Diese Verzerrungen lassen sich niemals vollständig beseitigen. Sämtliche Kartenprojektionen enthalten mindestens eine Form dieser Verzerrungen, weshalb man sich für bestimmte Vor- und Nachteile unter diesen Abbildungseigenschaften entscheiden muss:
- längentreue (äquidistante) Abbildung – einige Strecken sind korrekt abgebildet (beispielsweise für Streckenmessungen)
- flächentreue (äquivalente) Abbildung – alle Flächen sind dem Maßstab entsprechend korrekt abgebildet
- winkeltreue (konforme) Abbildung (beispielsweise zur Navigation oder für die Geodäsie)
- vermittelnde Verzerrungseigenschaften – Kompromisse zwischen Längen-, Flächen- und Winkeltreue.
Die Längentreue kann bei ebenen Karten nur begrenzt erreicht werden: in bestimmte Richtungen oder an bestimmten Punkten. Alle echten Abbildungen sind an den Berühr- bzw. Schnittkreisen längentreu. Eine absolute Längentreue in allen Punkten und allen Richtungen ist nicht möglich. Bei winkeltreuen Abbildungen ist die Längenverzerrung an einem bestimmten Punkt in jede Richtung (Azimut) gleich groß.
Der Globus bietet die Möglichkeit, alle metrischen Eigenschaften in einem bestimmten Maßstab nahezu korrekt wiederzugeben. Aufgrund des sehr kleinen Maßstabes reicht als Näherung für die Erdfigur – einem leicht abgeflachten Rotationsellipsoid – eine Kugel.
Längentreue Abbildungen
Diese Abbildungen sind nicht absolut längentreu, sondern lassen nur entlang weiterer Linien als den Berühr- bzw. Schnittkreisen längentreue Messungen zu.
- Quadratische Plattkarte und rechteckige Plattkarte (abstandstreue Zylinderabbildungen) – entlang der Meridiane
- Mittabstandstreue Azimutalprojektion – vom Mittelpunkt bzw. entlang der Radien
- Orthografische Azimutalprojektion – entlang der Kreise um den Berührpunkt
- Längentreue Kegelprojektion
- Sinusoidal-Projektion – entlang der Breitenkreise und des Mittelmeridians
- Werner Cordiform
Flächentreue Abbildungen
Diese Abbildungen stellen die Größe einer Fläche (z. B. eines Kontinents) korrekt dar. Die Form kann allerdings sehr stark verzerrt werden. Insbesondere am Kartenrand neigen diese Abbildungen zu starken Formverzerrungen.
- Peters-Projektion (Zylinder-Projektion, auch Gall-Peters-Projektion oder Gall-Projektion genannt)
- Projektion nach Walter Behrmann
- Albers-Kegelprojektion
- Flächentreue Azimutalprojektion nach J. H. Lambert
- Mollweide-Projektion von Carl Brandan Mollweide
- Hammer-Aitov-Projektion
- Briesemeister-Projektion
- Sinusoidal-Projektion
- Eckert-II-, -IV- und -VI-Projektion
- Goode-Projektion (zerschnittene Karten)
Winkeltreue Abbildungen
Winkeltreue Abbildungen werden insbesondere bei der Navigation in der Schifffahrt und im Flugverkehr zur Erstellung von Karten benötigt, aber auch in der Kristallographie.
Vermittelnde Abbildungen
Da keine Kartenabbildung alle Verzerrungen vollständig aufhebt, wurden einige vermittelnde Abbildungen als Kompromiss entwickelt. Bei ihnen wurde versucht die Verzerrungen zu minimieren.
- Kawraiski-VII-Projektion von Wladimir Kawraiski
- Eckert-I-, -III- und -V-Projektion (gleichabständige Breitenkreise)
- Robinson-Projektion
- Van-der-Grinten-Projektion
- Miller-Zylinderprojektion
- Winkel-Tripel-Projektion
- Wagner-IX-Projektion (auch Aitov-Wagner-Projektion genannt)[1][2]
Unechte Abbildungen (Pseudo-Abbildungen)
In normaler Lage bleiben bei echten Abbildungen die Längenkreise Geraden, die Breitenkreise werden als dazu rechtwinklige konzentrische Kreise, Kreisbögen oder Geraden abgebildet. Alle anderen Abbildungen fallen in die Gruppe der unechten bez. Pseudo-Abbildungen.
Unechte azimutale Abbildungen
- Aitov-Projektion 1889
- Hammer-Planisphäre (flächentreu)
Unechte Kegelabbildungen
- Bonnesche Projektion, unechte Kegelabbildung (Herzform)
- Stab-Wernersche Projektion, unechte Kegelabbildung (Herzform)
Unechte Zylinderabbildungen
Im Unterschied zu den echten Zylinderabbildungen sind die Meridianbilder (meist)(p) gekrümmte Linien.
- Globularprojektionen: Darunter fasst man alle frühen antiken und prämodernen Kartenentwürfe zusammen, denen noch fundierte mathematische Kenntnisse der Projektionsgeometrie fehlen. Es handelt sich durchwegs um empirische Hilfsnetze auf Basis wohlgeformter einfacher Kurven in einem Kreis.[3]
- Sinusoidal-Projektion
- Mollweide-Projektion von Carl Brandan Mollweide
- Eckert-Projektionen (I–VI) von Max Eckert-Greifendorff
- Robinson-Projektion
- Goode-Projektion (zerschnittene Karte)
Zerlappte Netze
- Goode-Projektion (zerschnittene Karte)
- Dymaxion-Projektion von Buckminster Fuller
- Waterman-Weltkarte
- Cahill-Keyes-Weltkarte
Abbildungen in der Praxis
- Schweizer Landeskoordinaten
- Gauß-Krüger-Koordinatensystem für Deutschland und Österreich
- UTM-Koordinatensystem – Universale Transversale Mercatorprojektion (weltumspannendes Zonensystem)
Literatur
- Eugen Kuntz: Kartennetzentwurfslehre. Herbert Wichmann Verlag, Karlsruhe 1983
- Karlheinz Wagner: Kartographische Netzentwürfe. Bibliographisches Institut Mannheim, 2. Auflage 1962
- Annoni et al.: Map Projections For Europe. European Commission (EUR 20120) (PDF-Datei; 19 MB)
Weblinks
- Kartennetzentwürfe (Böhm-Wanderkarten)
- Kartennetzentwürfe (Seite von M. Panitzki)
- Kartenprojektionen Europas (MapRef.org) (engl./teilw. deutsche Inhalte)
- Map Projection Overview (engl.), sehr umfassend
- Mathematical Cartography
- Hans Havlicek’s Picture Gallery of Map Projections
- verschiedene Projektionen im Panotools wiki
- Cartographical Map Projections (engl.)
- Gallery of Map Projections
- Kartennetzentwürfe vergleichen
Einzelnachweise
- http://www.progonos.com/furuti/MapProj/Dither/ProjMAz/projMAz.html#Wagner9 Info: Nicht erreichbar am 13. Oktober 2021.
- John J. G. Savard: The Aitoff-Wagner Projection. In: Miscellaneous Projections. 2012. Auf Quadibloc.com (englisch), abgerufen am 13. Oktober 2021.
- Rolf Böhm: Kartenprojektionen – Globularprojektionen, auf boehmwanderkarten.de;
Carlos Alberto Furuti: Map Projection: Premodern Projections: Globular Projections, auf progonos.com.