Robinson-Projektion
Die Robinson-Projektion ist ein Kartennetzentwurf, der 1961 von dem US-amerikanischen Kartographen Arthur H. Robinson entwickelt wurde.
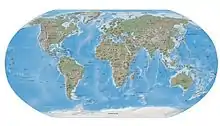
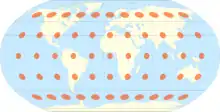
Die Robinson-Projektion ist eine vermittelnde Abbildung. Sie stellt keine Projektion im eigentlichen Sinne dar und sie basiert nicht wie andere Kartennetzentwürfe (z. B. Mercatorprojektion) auf einer geschlossenen mathematischen Formel, sondern auf einer Tabelle von Referenzpunkten, die empirisch ermittelt wurden. Alle Punkte zwischen diesen Referenzpunkten werden durch Interpolation ermittelt.
Der Vorteil der Robinson-Projektion ist, dass sie sehr natürlich wirkt. Sie weist nur im Bereich der Pole relativ große Abweichungen in Winkel und Fläche auf, die mit dem Abstand vom Zentralmeridian zunehmen. Sie ist jedoch in keinem Bereich verzerrungsfrei.
Geschichte
Die Robinson-Projektion geht auf eine Anfrage des US-amerikanischen Kartenverlags Rand McNally zurück, der 1961 an Robinson herantrat, um eine Projektion auszuwählen, die, neben anderen Bedingungen, ununterbrochen, möglichst verzerrungsarm und „augenfreundlich“ für den Betrachter sein sollte. Robinson konnte keine bekannte Projektion finden, die diese Kriterien erfüllte, und so beauftragte Rand McNally ihn mit der Entwicklung einer solchen.
Seit den 1960er Jahren wird die Robinson-Projektion in Karten von Rand McNally verwendet. Die National Geographic Society verwendete sie von 1988 bis 1998 für ihre Weltkarten, setzt seit 1998 jedoch stattdessen die Winkel-Tripel-Projektion ein.
Beschreibung
Die Robinson-Projektion wird nicht durch eine geometrische Projektion oder durch eine geschlossene Formel beschrieben, sondern durch Vorgabe von festen Werten für die Längen und Abstände der Breitenkreise von 0° bis 90° in Schritten von 5°. Breitenkreise werden als Geraden dargestellt, die parallel zum Äquator sind. Auch die Pole sind gerade Linien, ihre Länge beträgt das 0,5322fache der Äquatorlänge. Der Zentralmeridian, der als einziger Meridian auf eine gerade Linie abgebildet wird, besitzt von Pol zu Pol die 0,5072-fache Äquatorlänge. Punkte zwischen den vorgegebenen Punkten werden interpoliert, wobei unterschiedliche Interpolationsverfahren angewendet werden.[1]
Die folgende Tabelle gibt die Längen und Abstände der Breitenkreise an. Die Länge ist bezogen auf die Äquatorlänge, der Abstand auf den Abstand der Pollinie vom Äquator. Um diesen Abstand im selben Maßstab wie die Länge der Breitenkreise anzugeben, muss er mit der halben Länge des Zentralmeridians (0,2536) multipliziert werden.
| Breitengrad | Länge des Breitenkreises | Abstand vom Äquator |
|---|---|---|
| 00 | 1,0000 | 0,0000 |
| 05 | 0,9986 | 0,0620 |
| 10 | 0,9954 | 0,1240 |
| 15 | 0,9900 | 0,1860 |
| 20 | 0,9822 | 0,2480 |
| 25 | 0,9730 | 0,3100 |
| 30 | 0,9600 | 0,3720 |
| 35 | 0,9427 | 0,4340 |
| 40 | 0,9216 | 0,4958 |
| 45 | 0,8962 | 0,5571 |
| 50 | 0,8679 | 0,6176 |
| 55 | 0,8350 | 0,6769 |
| 60 | 0,7986 | 0,7346 |
| 65 | 0,7597 | 0,7903 |
| 70 | 0,7186 | 0,8435 |
| 75 | 0,6732 | 0,8936 |
| 80 | 0,6213 | 0,9394 |
| 85 | 0,5722 | 0,9761 |
| 90 | 0,5322 | 1,0000 |
Einzelnachweise
- Ningchuan Xiao: GIS Algorithms. Sage, Los Angeles/London/New Delhi/Singapore/Washington DC 2016, ISBN 978-1-4462-7432-3, S. 33–45.