Gnomonische Projektion
Eine gnomonische Projektion ist eine Zentralprojektion, bei der das Projektionszentrum im Mittelpunkt des abzubildenden Körpers liegt.
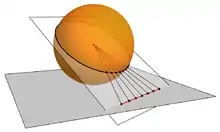
Die gnomonische Projektion wird verwendet:
- in der Kartografie mit Projektionszentrum im Erdmittelpunkt für Kartennetzentwürfe, vor allem für gnomonische Azimutalprojektionen, bei denen die Projektionsfläche eine Ebene ist (s. u.)
- in der Kristallografie mit Projektionszentrum im Mittelpunkt des Kristalls.
Die Art der Projektions- bzw. Abbildungsfläche ist prinzipiell beliebig; antikes Beispiel ist die Innenfläche einer Kugel bei einer der ältesten Sonnenuhren, der Skaphe. Je nach Geometrie der Abbildungsfläche wird die Abbildung jedoch zu allen oder zu einzelnen Rändern hin stark verzerrt; für topografische Karten ist die gnomonische Projektion deshalb nicht geeignet.
Etymologie und Historisches
Der Begriff gnomonische Projektion leitet sich ab von Gnomon (γνόμον), dem griechischen Wort für den Schattenstab einer Sonnenuhr, bei der die Himmelssphäre mit der Sonne zentral aus der Gnomonspitze (Nodus) auf das Zifferblatt abgebildet wird.
Mit der Spitze des Gnomons als schattenwerfendes Projektionszentrum wurde z. B. bereits in der Antike der Stand der Sonne in einer Sonnenuhr abgebildet und zur Anzeige der Tageszeit benutzt. Eine Konstruktionsvorschrift für eine Sonnenuhr, die einen Gnomon enthält, ist als Das Analemma des Vitruv überliefert.
Gnomonische Azimutalprojektion
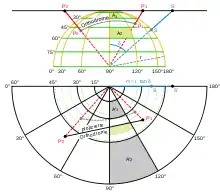
Gnomonische Azimutalprojektionen sind „geradentreu“, d. h. alle Großkreise auf der Erdoberfläche und damit alle Orthodromen werden als Geraden abgebildet. Will man von einem Punkt auf kürzestem Weg zu einem anderen navigieren, so kann man daher in einer Karte mit gnomonischer Azimutalprojektion die Wegstrecke durch Verbinden der Punkte mit einer geraden Linie ermitteln. Deshalb werden diese Karten zusammen mit winkeltreuen Karten in der Navigation zur See und in der Luft sowie in der Funknavigation angewendet.
Die Kristallografie nutzt aus, dass Pole tautozonaler Flächen in gnomonischer Azimutalprojektion auf Geraden liegen.
Die gnomonische Azimutalprojektion erlaubt die Abbildung des am Projektionszentrum beginnenden offenen Halbraumes, in dem die Abbildungsebene liegt. Ein in der Begrenzung des Halbraumes liegender Großkreis wird ins Unendliche projiziert (z. B. in der Abb. rechts der Äquator). Aufgrund Verzerrungen, die mit steigender Entfernung vom Mittelpunkt der Projektion stark zunehmen, beschränkt man die Projektion meist auf einen Winkelbereich von höchstens 60° um die Mittelachse.
Gnomonische Projektionen in der Kartografie
Normale (polare) Lage
Ist die Projektionsebene einer gnomonischen Azimutalprojektion in normaler Lage, d. h., sie berührt die Erde in einem Pol, so werden die Breitenkreise als konzentrische Kreise um den Pol und die Meridiane als radiale Geraden abgebildet. Der Kartennetzentwurf lässt sich mit Hilfe von Zirkel und Lineal ausführen.
Die Abbildungsgleichungen in dieser Lage lauten für die Polarkoordinaten der Karte:
mit
- Azimut
- geographischer Länge
- Maßstabsfaktor
- Radius
- Breitenkomplement = 90° − geographische Breite.
Transversale Lage
Der Berührungspunkt liegt auf dem Äquator. Die Meridiane werden als parallele Geraden abgebildet, die Breitenkreise als Hyperbeln. Der Äquator wird zu einer Geraden, welche die Meridiane senkrecht schneidet.
Schiefe Lage
Die Karte berührt einen beliebigen Punkt der Erdoberfläche (hier Japan). Sie bildet die Meridiane ebenfalls als Geradenbündel ab, die Breitenkreise werden zu Kegelschnitten.
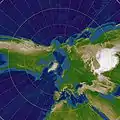Normale Lage:
Nordpol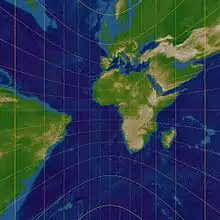
Transversale Lage:
Äquator (0° geogr. Länge)
Schiefe Lage:
Japan
Veranschaulichung
Wenn man einen Globus von innen beleuchtet (mit nahezu punktförmiger Lichtquelle im Zentrum des Globus), so dass die Globusoberfläche an eine ebene Wand oder die Zimmerdecke projiziert wird, so entspricht dieses Abbild an der Wand der gnomonischen Azimutalprojektion.
Wenn die Globusachse senkrecht zur Decke steht, bilden sich alle Parallelkreise als konzentrische Kreise ab, bei schräger Lage als Ellipsen und Hyperbeln; die Meridiane bleiben hingegen gerade.
Weblinks
- Institut für diskrete Mathematik und Geometrie der TU Wien: gnomonische Azimutalprojektion der Erde – interaktiv
- Institut für diskrete Mathematik und Geometrie der TU Wien: gnomonische Kegelprojektion der Erde – interaktiv
- Böhm Wanderkarten: Gnomonische Azimutalprojektion – u. a. in verschiedenen Lagen