Fischaugenobjektiv

Das Fischauge (englisch fisheye beziehungsweise fisheye lens) bezeichnet in der Fotografie ein spezielles Objektiv, das mit der dazu nötigen Verzeichnung ein komplettes Gesichtsfeld abbilden kann. Im Gegensatz zu konventionellen Nicht-Fischaugen-Objektiven, die eine senkrecht zur optischen Achse stehende Objektebene proportional abbilden (gnomonische Projektionsweise, siehe unten: Abbildungsfunktionen), bilden Fischaugenobjektive eine Hemisphäre oder mehr, mit deutlichen aber nicht übermäßigen Verzerrungen, auf der Bildebene ab. Gerade Linien, die nicht durch die Bildmitte laufen, werden gekrümmt abgebildet; die Abbildung ist stark tonnenförmig (siehe Verzeichnung). Es bildet Flächenverhältnisse oder radiale Abstände meist getreuer ab als ein gewöhnliches, gnomonisch projizierendes Weitwinkelobjektiv und besitzt einen sehr großen Bildwinkel (meist 180° in der Bilddiagonalen, im Extremfall sogar bis zu 220°, bei Entwürfen sogar 270° und 310°[1]). Bildwinkel von 180° oder mehr sind mit der konventionellen Projektionsweise nicht erreichbar. Trotz der außergewöhnlich großen Bildwinkel ist der Helligkeitsabfall zum Bildrand hin leichter korrigierbar, als bei Weitwinkelobjektiven, weil der Abbildungsmaßstab zum Bildrand nicht so stark zunimmt, und das Licht nicht so große Flächen ausleuchten muss.

Modernes Fischaugen-Zoomobjektiv mit einer Brennweite von 8–15 mm

Lichtstarkes Fischaugenobjektiv Laowa 4 mm f/2,8 von Venus Optics mit einem Bildwinkel von 210° und einem Gewicht von 135 Gramm für Micro Four Thirds

Auf der Photokina 1970 vorgestellt und 1972–1983 gefertigt.
Das Fisheye-Nikkor 6mm f/2.8 hatte den bisher größten Bildwinkel von 220° im KB-Format.

Das weltweit erste in Serie produzierte Fischaugenobjektiv wurde 1962 von Nikon vorgestellt (Fisheye-Nikkor 1:8, f = 8 mm).[2] Das Objektiv ragte weit in das Kameragehäuse hinein, so dass der Spiegel hochgeklappt und arretiert, und ein externer Sucher am Blitzsteckschuh befestigt werden musste.

Mittlerweile gibt es eine Vielzahl an Herstellern, die Fischaugenobjektive produzieren. Für einäugige Spiegelreflexkameras sind sie meist als Retrofokusobjektive ausgeführt, damit der Spiegel zwischen Verschluss und Hinterlinse genug Platz hat.

Moderne spiegellose Kamerasysteme mit erheblich kürzeren Auflagemaßen ermöglichen durch den geringen Abstand von Optik und Sensor weniger Aufwand für Retrofokuskonstruktionen. Das verringert Gewicht und Preis oder ermöglicht bei gleichem Aufwand größere Bildwinkel oder höhere Lichtstärken[3].

Miniaturfischaugenobjektive für sehr kleine Sensoren, wie sie in Überwachungskameras oder Action-Camcorder eingesetzt werden, sind noch preiswerter, so dass noch größere Bildwinkel bis 280°[4] angeboten werden, und nicht mehr kosten, als ein 180°-Retrofokus-Fischaugenobjektiv für das Kleinbildformat. Inzwischen gibt es auch vergrößerte Varianten von Miniaturfischaugen mit Bildwinkeln bis zu 250° für spiegellose Systemkameras.[5]

Typen

**Tafel 1: Typen der Formatausnutzung**
zirkular		beschnittener Kreis	Vollformat
circular		cropped circle	full frame

3:2	52 % Sensor	78 % Bildfeld, 92 % Sensor	59 % Bildfeld
4:3	59 % Sensor	86 % Bildfeld, 90 % Sensor	61 % Bildfeld
Zirkular-Fischauge für das Kleinbildformat			Vollformat-Fischauge mit rudimentärer Streulichtblende
Aufnahme mit Zirkular-Fischauge		Kleinbild-Zirkular-Fischauge an DX-Format-Kamera	Innenraum mit Vollformat-Fischauge fotografiert

Man unterscheidet Fischaugen-Objektive einerseits nach ihrer Projektionsart (siehe Abbildungsfunktionen weiter unten) und nach ihrem Bildkreisdurchmesser im Verhältnis zum Aufnahmeformat.

Zirkular

Fischaugenobjektive, deren Bildkreisdurchmesser (höchstens) so groß ist wie die kürzere Kante des Aufnahmeformates der Kamera, heißen Zirkular-Fischauge (auch „Kreisbild-Fischauge“ oder „Rundbild-Fischauge“), weil sie ein kreisrundes Bild innerhalb des rechteckigen Aufnahmeformates entwerfen. Der Bildkreis des Objektivs wird zu 100 % genutzt. In Tafel 1 ist die größtmögliche Sensorausnutzung angegeben; sie fällt durch einen praktisch etwas kleineren Bildkreis geringer aus. Um den Bildkreis nicht zu beschneiden, haben Zirkular-Fischaugen keine Streulichtblende. Zirkulare Fischaugen sind die erste Wahl, wenn möglichst viel von der Umgebung (gewöhnlich eine Halbkugel) erfasst werden soll. Die zuerst entwickelten Fischaugenobjektive waren Zirkular-Fischaugen. Mangels eines Vollformat-Fischauges einen rechteckigen Bereich auszuschneiden verringert die Sensor- oder Filmausnutzung weiter auf maximal 31 % (3:2) oder 36 % (4:3) und wäre denkbar ungünstig.

Vollformat

Fischaugenobjektive, deren Bildkreisdurchmesser (mindestens) so groß ist wie die Diagonale des Aufnahmeformates der Kamera, heißen „Vollformat-Fischauge“ (auch „Diagonal-Fischauge“ wegen der Doppeldeutigkeit des Begriffs „Vollformat“ für Sensorausnutzung oder Sensorgröße). Sie erreichen ihren größten Bildwinkel (gewöhnlich 180°) nur über die Bilddiagonale; ihre horizontalen und vertikalen Bildwinkel sind entsprechend kleiner und Teile des Bildfeldes des Objektivs werden nicht genutzt. Der Sensor wird dagegen zu 100 % ausgenutzt. Die Streulichtblende fällt sehr klein aus und begrenzt das Bildfeld auf einen annähernd rechteckigen Bereich, der nur wenig über das vorgesehene Aufnahmeformat reicht. Als Fischaugen in der allgemeinen Fotografie populär wurden, begannen die Kamerahersteller Vollformat-Fischaugen zu entwickeln. Das rechteckige Format ist am angenehmsten für die direkte Wiedergabe der originalen Bilder (ohne Umrechnung).

Beschnittener Kreis

Wenn die Kamera nicht das Sensorformat hat, für das das Fischaugenobjektiv vorgesehen ist, ändern sich Bildwinkel und Formatausnutzung. Mit bestimmten Kombinationen lässt sich ein nutzbares Bildfeld in Form eines beschnittenen Kreises als Zwischenformat von Kreis- und Vollbild erzielen. Es ergeben sich eine gute Sensorausnutzung und meist weniger Verluste beim rechteckigen Beschneiden der in einen anderen Projektionstyp umgewandelten Bilder.

Entweder wird ein Zirkular-Fischauge für das Kleinbildformat an einer APS-C- oder DX-Kamera oder ein Vollformat-Fischauge für das DX-Format an einer vollformatigen Kleinbildkamera verwendet. Im zweiten Fall beschneidet die Streulichtblende das Bild und muss abgenommen werden. Wenn sie nicht abnehmbar ist, kann sie mit einem Werkzeug gekürzt werden (Rasur des Objektivs). Einige Fischaugen-Zoomobjektive können ebenfalls einen beschnittenen Kreis erzielen.

Im Idealfall ist das Bildfeld ein zweiseitig beschnittener Kreis. Der Bildkreisdurchmesser ist dann (höchstens) so groß wie die längere Seite des Aufnahmeformates. Der Bildwinkel wird z. B. beim Querformat an den runden Bildkanten sowohl diagonal als auch horizontal maximal; nur vertikal ist er kleiner. In der Praxis gibt es auch den dreiseitig beschnittenen Kreis, wenn der Sensorbereich nicht mittig zum Bildkreis ist (z. B. flächentreues Sigma 8 mm Fisheye [älteres Modell mit Blende F/4] und Kamera mit APS-C-Sensor), oder den vierseitig beschnittenen Kreis, wenn die Abbildungsfunktion einen größeren Bildkreis erzeugt (z. B. winkellineares Canon 8-15 mm Fisheye bei 8 mm und Kamera mit APS-C-Sensor).

Bei der Umwandlung in die stereografische Projektion kann man nach dem rechteckigen Beschneiden ein Vollformatbild mit 180° diagonalem Bildwinkel erhalten (Von einem Vollformatbild ausgehend, wäre die stereografische Projektion kissenförmig. Das rechteckige Beschneiden würde die Kissenspitzen entfernen und damit den diagonalen Bildwinkel reduzieren). Evtl. sind Bildwinkel von 180° nicht mehr mit dem Originalformat, sondern nur mit einem breiteren Format (z. B. 16 : 9) des umgewandelten Bildes möglich.

Brennweite

Vollformat-Fischaugen haben für das Kleinbildformat Brennweiten von etwa 16 mm und liegen damit im Bereich starker Weitwinkelobjektive. Für das gängige APS-C- oder DX-Format digitaler Spiegelreflexkameras mit Cropfaktor 1,5…1,6 beträgt die Brennweite je nach Projektionsart etwa 8 bis 10 mm.

Zirkular-Fischaugen haben die kürzeren Brennweiten. Die Brennweite liegt beim Kleinbildformat bei etwa 8 mm und beim APS-C- oder DX-Format bei etwa 4,5 mm.

Zoom-Fischaugen schließen mit ihrem Brennweitenbereich das zirkulare und das vollformatige Fischauge ein, wenn sie für diesen Zweck ausgelegt und für das vorgesehene Aufnahmeformat verwendet werden.[6] Oder sie schließen die Lücke zwischen einem Vollformat-Fischauge und einem Weitwinkel- oder Universal-Zoomobjektiv und behalten dabei die tonnenförmige Verzeichnung im gesamten Zoombereich.[7]

Fischaugen für andere Formate (z. B. Mittelformat – Cropfaktor ca. 0,5 oder FourThirds – Cropfaktor 2) haben proportional zur Formatgröße entsprechend andere Brennweiten.

Bildwirkung

Fischaugen-Bild (links) und entzerrte Aufnahme (rechts)

Ein Fischaugenbild soll dem Bild entsprechen, welches ein Fisch hat, der von unten durch die Wasseroberfläche oder seitlich aus einem Aquarium schaut; so ist auch der Name des Objektivs entstanden (siehe unten Abschnitt Unterwasserblick).

Zwischen visueller Betrachtung des Objektes und der Betrachtung des Bildes gibt es Abweichungen, weil man durch Kopf- und Augenbewegung immer zentral auf jedes Detail schaut und es verzerrungsfrei wahrnimmt, die Optik aber Randdetails schräg erfasst.

Krümmung

Die Abbildung einer langen, geraden Straße auf ganzer Länge muss folgende widersprüchliche Eigenschaften im Bild vereinen: In Bildmitte sind die Straßenränder parallel, und an beiden Bildseiten laufen die Straßenränder zu Fluchtpunkten zusammen. Das ist nur mit tonnenförmiger Verzeichnung möglich. Sie ist eine Voraussetzung für Fischaugen, denn nur so sind Bildwinkel von 180° und mehr möglich.

Geraden durch die Bildmitte bleiben Geraden. Bei Geraden außerhalb der Bildmitte wird die Krümmung desto stärker, je weiter sie an der Mitte vorbeigehen. Lange Kanten im Randbereich weisen eine starke Richtungsänderung auf. Das verfremdet vor allem sehr große Objekte.

Einsetzen kann man das Fischauge für Objekte, die kaum gerade Linien haben, z. B. für Panoramaaufnahmen von Landschaften. Für Objekte mit vielen geraden Kanten (Architektur) ist ein Fischauge nicht zu empfehlen. In Innenräumen ist der große Bildwinkel praktisch, weil man mit einem Bild einen ganzen Raum abbilden kann. Entweder akzeptiert man dann die gebogenen Linien, oder man wandelt das Bild so um, dass z. B. die Senkrechten und die zentralen Fluchtlinien gerade werden (Pannini-Projektion[8][9]).

Personen am Bildrand stehen scheinbar krumm. Sie erscheinen nach außen durchgebogen. Dies kann man als Kompromiss für eine geringe Deformation der Köpfe (siehe Abschnitt Deformation) hinnehmen. Alternativ beseitigt eine geeignete Umwandlung (z. B. in die Pannini-Projektion) die Durchbiegung des Körpers bei ein wenig mehr verzerrten Köpfen.

Skalierung

Nebeneinander liegende Objekte gleicher Größe werden je nach Lage im Bildfeld unterschiedlich groß dargestellt. Sie weisen unterschiedliche Abbildungsmaßstäbe auf, so dass man von einer Maßstabsverzerrung sprechen kann.

Die hier gemeinte Skalierung entspricht der Kartografie und ist anders definiert als die Maßstabsverzerrung in der konventionellen Fotografie.

Maßstabsverzerrung in der konventionellen Fotografie ist die lokale Größenänderung bei der Abbildung einer senkrecht zur optischen Achse stehenden Objektebene auf die Bildebene. Das führt nebenbei auch zur Verzeichnung. Ohne Maßstabsverzerrung können bei dieser Betrachtungsweise auch Superweitwinkelobjektive sein. So werden auch seitliche Kreise, die senkrecht zur optischen Achse stehen, im gleichen Maßstab abgebildet, als stünden sie in der Mitte (und bleiben Kreise). Der Maßstab in der konventionellen Fotografie hängt von dem auf die optische Achse projizierten Abstand ab und nicht von der tatsächlichen (schrägen) Entfernung von der Eintrittspupille und beschreibt die Größe senkrecht zur optischen Achse.

Ersetzt man die ebenen Kreise durch räumliche Kugeln[10], liegen die gesehenen Kugelhorizonte auf zur Eintrittspupille konzentrischen Kugelschalen und nicht mehr auf der Ebene der vorherigen Kreise. Der schrägstehende Kugelhorizont führt bei der Projektion auf die Objektebene zu einer elliptischen (bei großen Objekten eiförmigen) Deformation und zu einer Vergrößerung. Fischaugen beziehen sich nicht auf eine Objektebene (eher auf eine Objektschale), wodurch die Größenänderung anders ausfällt.

Skalierung beschreibt die Größenänderung eines kleinen Details auf einer zur Eintritsspupille konzentrischen Kugelschale in Relation zur mittigen Abbildung. Die Skalierung bezieht sich auf ein Objekt mit gleicher direkter Entfernung zur Eintrittspupille und auf die senkrecht zur Objektrichtung erscheinende Größe. Die Abweichung vom Maßstab in der Bildmitte ist die Skalierung. Sie ändert scheinbar die Tiefenstaffelung nebeneinander liegender Objekte. Die Berechnung einer Tissotschen Indikatrix macht die Skalierung über die Größe der Verzerrungsellipsen deutlich (Skalierung ist proportional zur Wurzel der Flächen der Verzerrungsellipsen).

Beim konventionellen Superweitwinkel werden Randdetails, bezogen auf die direkte Entfernung, größer dargestellt. So tritt die Bildmitte in den Hintergrund, und es entsteht ein scheinbar zu tiefer Raum. Das führt dazu, dass ein quadratischer Raum wie ein Korridor aussieht. Beim Fischauge ist die Skalierung von Randdetails je nach Abbildungstyp deutlich kleiner, ganz aufgehoben (flächentreu) oder im Extremfall gegenläufig (orthographisch: Tiefenkompression). Die scheinbare Tiefe des quadratischen Raumes ändert sich wenig. Er erscheint dafür auseinandergebogen (siehe Abschnitt Krümmung).

Tiefendehnung

Hintereinanderliegende Objekte (an der gleichen Bildstelle) scheinen auseinanderzurücken. Dieser Effekt ist unabhängig davon, ob das Objektiv ein Fischauge oder ein Superweitwinkel ist. Mit der bei allen Fischaugen kurzen Brennweite ist die Tiefendehnung sehr ausgeprägt, so dass der Vordergrund sehr gut aus dem Hintergrund herausgelöst werden kann. Durch den Fischaugen-Bildwinkel von 180° kann man für extreme Effektbilder sehr nahe an das Objekt gehen und bekommt sogar bei Frontlinsenkontakt meist das gesamte Objekt auf das Bild.

Deformation

Die Deformation ist eine anders definierte optische Verzerrung als die Verzeichnung.

Verzeichnung beschreibt die Verzerrung auf einer zur optischen Achse senkrechten Fläche bei der Abbildung. Verzeichnungsfrei können auch Superweitwinkelobjektive sein. So werden auch seitliche Kreise, die senkrecht zur optischen Achse liegen, wieder als Kreise abgebildet.

Ersetzt man die ebenen Kreise durch räumliche Kugeln[10], liegen die gesehenen Kugelhorizonte auf zur Eintrittspupille konzentrischen Kugelschalen und nicht mehr auf der Ebene der vorherigen Kreise. Der schrägstehende Kugelhorizont führt bei der Projektion auf die Objektebene zu einer elliptischen (bei großen Objekten eiförmigen) Deformation. Fischaugen beziehen sich nicht auf eine Objektebene (eher auf eine Objektschale), wodurch die Deformation anders ausfällt.

Deformation beschreibt die Verzerrung eines kleinen Details auf einer zur Eintrittspupille konzentrischen Kugelschale. Die Berechnung einer Tissotschen Indikatrix macht die Deformation über die Streckung der Verzerrungsellipsen deutlich (Verhältnis von Haupt und Nebenachse).

Während bei konventionellen Weitwinkelobjektiven räumliche Randdetails von der Mitte weg auseinandergezogen sind, machen Fischaugen das Gegenteil und stauchen diese. Die Deformation ist nicht so stark und erst bei stärkerer seitlicher Lage wahrnehmbar. Damit ist das Fischauge gut für Aufnahmen innerhalb einer Menschenmenge oder von Personen an einem Tisch geeignet. Dabei sollte man aber keiner Person zu nahe kommen, um entstellende Effekte zu vermeiden. Für eine möglichst perfekte Personendarstellung empfiehlt sich die Umwandlung in die winkeltreue Abbildung (keine Stauchung kleiner Objekte).

Abbildungsfunktionen

Die Abbildungsfunktion bestimmt die Eignung für einen bestimmten Einsatzzweck. Bei der Umrechnung in andere Darstellungen oder beim Zusammenfügen zu Panoramen ist die richtige Abbildungsfunktion entscheidend für die Qualität des Endergebnisses.

Fundamentale Abbildungen

Verschiedene Abbildungsfunktionen

Unterschiedliche Verzeichnung

Von den vielen möglichen Abbildungsfunktionen zeichnen sich die fundamentalen durch die originalgetreue Wiedergabe bezüglich eines Parameters aus. Der Projektionstyp einer Optik ist der Name der Projektion der ähnlichsten fundamentalen Abbildung.

Zum Vergleich – normales (Nicht-Fischauge-)Objektiv:

gnomonisch (verzeichnungsfrei)
wirkt wie die Lochkamera. Gerade Linien sind auch auf dem Bild gerade. Große Bildwinkel erfordern bei Retrofokusobjektiven einen extremen Aufwand und führen zu sehr hohen Preisen für ein solches Objektiv.

Ultraweitwinkelobjektive können die Brennweiten von Fischaugen-Objektiven haben; sie sind aber wegen ihrer Abbildungsart trotzdem keine Fischaugen.

Räumliche Objekte nahe dem Bildrand werden verzerrt abgebildet: Sie sind in radialer Richtung gestreckt. Sie erscheinen am seitlichen Bildrand daher in der Abbildung zu breit, und am Bildrand stehende Personen werden dann zum Beispiel dicker abgebildet, als sie sind, und bekommen „Eierköpfe“.[10]

Ebene Objektflächen, die genau senkrecht zur optischen Achse stehen, werden maßstabstreu und verzeichnungsfrei abgebildet. Gibt es mehrere solcher Flächen, dann hat jede Fläche entsprechend ihrer auf die optische Achse projizierten Entfernung einen eigenen Maßstab.

Fischaugen können verschiedene Abbildungsfunktionen haben. Es folgen einige Spezialfälle:

winkeltreu (stereografisch)
wäre ideal für die meisten fotografischen Zwecke, denn Objekte am Bildrand werden nur geringfügig verzerrt. Objekte, deren Abbild in allen Richtungen nur wenig ausgedehnt ist, werden praktisch unverzerrt abgebildet. Personen z. B. werden mit den richtigen Proportionen wiedergegeben, weder zu schlank noch zu dick. Ein Objekt erscheint am Bildrand jedoch größer als in der Bildmitte, bei gleicher Entfernung von der Kamera, d. h. Objekte am Rand erscheinen näher, als sie sind. Für gängige digitale Spiegelreflexkameras bietet Samyang Optics eine Optik mit annähernd winkeltreuer Abbildung an.[11][12] Sie wird unter verschiedenen Markennamen angeboten, in Deutschland unter „Walimex“. Für andere Fischaugen-Typen kann die winkeltreue Abbildung durch Software realisiert werden. Populär ist die als „Little planet“[13] bezeichnete stereografische Darstellung mit dem Nadir in Bildmitte, die aber ein Fischauge mit weit über 180° Bildwinkel erfordert oder mit Panoramasoftware erzeugt werden kann.
äquidistant (linear geteilt)
Solche Objektive ermöglichen Winkelmessungen auf dem Bild in radialer Richtung (z. B. für Sternkarten). Diese Abbildungsart eignet sich besonders für extreme Bildwinkel über 180°. Mittige Objekte werden nicht so klein wie bei der winkeltreuen Abbildung; und Objekte am Bildrand werden im Gegensatz zur flächentreuen Abbildung radial nicht komprimiert. Sie wirken in radialer Richtung dennoch gestaucht, weil sie quer zur radialen Richtung vergrößert sind. Personen erscheinen etwas schlanker, als sie sind. Der Abstand von Objekten am Bildrand wird weniger unterschätzt als bei winkeltreuer Abbildung.

Die meisten Rundbild-Fischaugen, wie z. B. das Canon FD 1:5,6 / 7,5 mm, bilden so ab. Software zur Panoramaerstellung, beispielsweise Hugin, gehen von dieser Projektionsart aus.

Bei einer Umrechnung in diesen Projektionstyp sind mathematisch Bildwinkel über 360° möglich. Dabei wiederholt sich die Darstellung in ringförmigen Zonen (Mehrfachabbildung).

flächentreu (equisolid angle = raumwinkelgleich)
Es entsteht das gleiche Bild, als wäre an der Kameraposition eine verspiegelte Kugel platziert, die man aus großer Entfernung, verglichen mit ihrem Durchmesser, betrachtet. Die Fläche, die das Abbild eines Objekts auf dem Bild einnimmt, ist proportional zum Raumwinkel, in dem es von der Kameraposition aus gesehen erscheint. Die Entfernungen der Objekte von der Kamera werden deshalb richtig eingeschätzt. Solche Objektive eignen sich besonders, um im Bild Bedeckungsgrade zu bestimmen (z. B. durch Vegetation oder durch Bebauung, oder zur Bewölkungsgradbestimmung). Die radiale Stauchung von randnahen Objekten ist noch etwas größer als bei äquidistanter Projektion. Viele Vollformat-Fischaugen bilden (annähernd) flächentreu ab.
orthografisch
wirkt wie eine Kugel, die aus großer Entfernung betrachtet wird, und auf die die Umgebung projiziert wurde, mit dem Kugelmittelpunkt als Projektionszentrum. Solche Objektive ermöglichen die Analyse von Beleuchtungsverhältnissen. Seitliche Lichtbereiche tragen weniger zur Helligkeit auf einer senkrecht zur optischen Achse angeordneten Ebene bei und werden entsprechend kleiner abgebildet. Standardmäßig wird der maximal mögliche und für die Beleuchtungsanalyse erforderliche Bildwinkel von 180° abgebildet, obwohl die Verzerrungen nur innerhalb von 120° erträglich sind. Für die bildmäßige Fotografie ist dieser Typ wegen der ausgeprägten Verzerrungen eher unvorteilhaft, Objekte nahe dem Bildrand werden radial noch weit stärker gestaucht als bei flächentreuer Abbildung.

Das Nikon OP Fish-eye NIKKOR 1:5,6/10 mm folgt dieser Projektionsweise („OP“ = orthographic projection); es besitzt eine asphärische Frontlinse, um diese schwierige Projektionsart zu realisieren. Auch Fischaugen-Vorsätze haben meistens eine annähernd orthografische Projektion.

Parameter

Umgebungskugel mit Motivmitte und Z-Achse nach hinten (Stereobild für Kreuzblick)

Kugelkoordinaten

Ebene Polarkoordinaten und kartesische Transformation

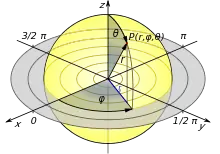
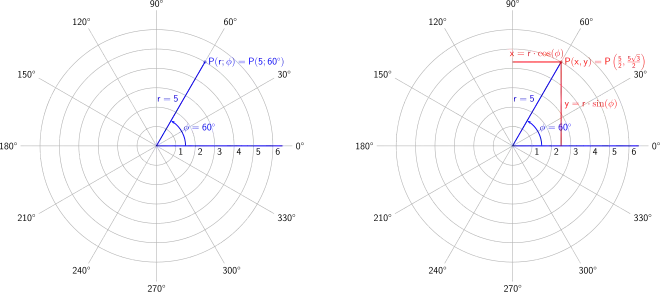
Die Umgebung wird in Kugelkoordinaten erfasst, wobei die z-Achse die optische Achse des Objektivs ist und auf die Mitte des zu fotografierenden Bereichs zeigt. Der Koordinatenursprung ist die Eintrittspupille. Die Lage eines Objektes wird mit $(r,\varphi ,\theta )$ bestimmt. Der Kugelradius $r$ hat theoretisch keinen Einfluss auf die Abbildungsfunktion (reale Objektive: siehe Abschnitt Hinweise). So können alle Objekte auf genau einen Abstand skaliert werden, und es entsteht eine Umgebungskugel. Für den Radius der Umgebungskugel wählt man die Brennweite des Objektivs ( $r$ = $f$ ).

In kartesischen Koordinaten liegt die Bildebene bei $z$ = $f$ und berührt die Umgebungskugel am Pol ( $\theta =0$ ). Auf das Bild werden ebene Polarkoordinaten angewendet. Die Lage eines Bilddetails ist durch $(r,\phi )$ beschrieben. In dieser geometrischen Anordnung lassen sich die Abbildungsfunktionen gut veranschaulichen und meist auch konstruieren. Die Objektkoordinaten $\varphi$ (Azimut) und $\theta$ (Polarwinkel) bilden sich in den Bildkoordinaten $\phi$ (Azimut) und $r$ (Radius) ab.

Das Prinzip ist das gleiche wie beim azimutalen Kartennetzentwurf der Erde. Dort gilt $\phi =\varphi$ . Jedoch wird die Umgebungskugel im Gegensatz zur Erdkugel von innen betrachtet. Die Vorderseite der Bildebene zeigt die Umgebung dann spiegelbildlich. Für die hier erforderliche rückwärtige Betrachtung sind die Bildkoordinaten (polar und 2D-kartesisch) anders orientiert, so dass die Azimut-0°-Richtung und der Azimut-Umlaufsinn sich zwischen Umgebung und Bild unterscheiden kann. Azimut-Winkelabstände werden unverfälscht abgebildet, und Abbildungsfunktion und Azimut beeinflussen sich nicht. Damit liegt eine azimutale Abbildung vor.

Die Abbildungsfunktion $\mathbf {g}$ beschreibt, wie ein Objekt im Polarwinkel $\theta$ auf dem Bild um Radius $r$ aus der Mitte verschoben erscheint. Das Objektiv hat die (zentrale) Brennweite $f$ . Mit $f$ = 1 wird aus $\mathbf {g}$ die normierte Abbildungsfunktion $\mathbf {h}$ .

r=\mathbf {g} (\theta ,f)=f\cdot \mathbf {h} (\theta )

Seitliche Objekte erscheinen, auf dem Bild verglichen mit der Mittenlage, in anderer Größe, die sich meist auch meridional und sagittal unterscheidet.

meridionale Skalierung:

S_{m}={\frac {\mathrm {d} \mathbf {h} (\theta )}{\mathrm {d} \theta }}

sagittale Skalierung:

S_{s}={\frac {\mathbf {h} (\theta )}{\sin \theta }}

Daraus lassen sich Raumwinkelskalierung $S_{\Omega }$ , lineare (effektive) Skalierung $S$ und Deformation $D$ ableiten:

S_{\Omega }=S_{m}\cdot S_{s}

S={\sqrt {S_{\Omega }}}

D={\frac {S_{m}}{S_{s}}}

Bei den fundamentalen Abbildungsfunktionen fällt auf, dass es eine Potenz $B$ zwischen Deformation und Skalierung gibt, die unabhängig von $\theta$ ist: $D=S^{B}$ . Weil $D$ und $S$ aus $S_{m}$ und $S_{s}$ abgeleitet sind, ergibt sich auch zwischen $S_{m}$ und $S_{s}$ eine $\theta$ -unabhängige Potenz $N$ mit $S_{m}=S_{s}^{N}$ . Dieses $N$ wird zur Kennzahl der jeweiligen fundamentalen Funktion.

B={\frac {2\,(N-1)}{N+1}}

(Balance zwischen Deformation und Skalierung)

Der Krümmungsfaktor $C$ (curvature) ist die Krümmungszunahme im paraxillaren Bereich.

C={\frac {N-2}{3-N}}

(Krümmung negativ bei tonnenförmiger Verzeichnung)

Die Spezialfälle C = 0 (krümmungsfrei, verzeichnungsfrei), D = 1, S_m = 1, S = 1, S_s = 1 (konstanter Maßstab der jeweiligen Größe) führen zu den fünf fundamentalen Grundfunktionen des vorherigen Abschnitts und der folgenden Tabelle. Keine dieser Grundfunktionen kann mehr als einen Spezialfall abdecken. Gnomonische (C = 0) Normal- und Teleobjektive erfüllen scheinbar alle Spezialfälle, weil die Maßstäbe D, S_m, S und S_s wegen des kleinen Bildwinkels nur wenig vom Wert eins abweichen, wodurch die Abweichungen kaum wahrgenommen oder durch die Betrachtungsperspektive kompensiert werden (Bildbetrachtungswinkel ähnlich Aufnahmewinkel).

Tabelle 1: Fundamentale Funktionen
Projektionstyp (fundamental)	gnomonisch	Fischauge
Projektionstyp (fundamental)	gnomonisch	winkeltreu	äquidistant	flächentreu	orthografisch
Beispiel Zylindertunnel
Skizze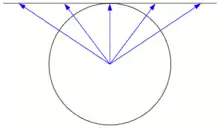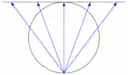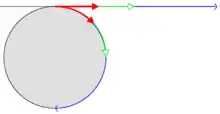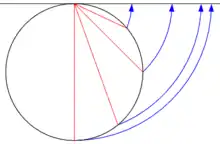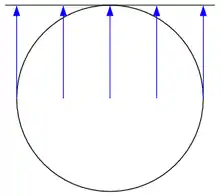
$N$	$2$	$1$	$0$	$-1$	$\infty$
$B$	${\tfrac {2}{3}}$	$0$	$-2$	$\infty$	$2$
$C$	${\boldsymbol {C}}=0$	$-{\tfrac {1}{2}}$	$-{\tfrac {2}{3}}$	$-{\tfrac {3}{4}}$	$-1$
Abbildungsfunktion	${\boldsymbol {r=f\tan \theta }}$	${\boldsymbol {r=2f\tan {\frac {\theta }{2}}}}$	${\boldsymbol {r=f\,\theta }}$	${\boldsymbol {r=2f\sin {\frac {\theta }{2}}}}$	${\boldsymbol {r=f\sin \theta }}$
meridionale Skalierung	$S_{m}={\frac {1}{\cos ^{2}\theta }}$	$S_{m}={\frac {1}{\cos ^{2}{\frac {\theta }{2}}}}$	${\boldsymbol {S_{m}=1}}$	$S_{m}=\cos {\frac {\theta }{2}}$	$S_{m}=\cos \theta$
sagittale Skalierung	$S_{s}={\frac {1}{\cos \theta }}$	$S_{s}={\frac {1}{\cos ^{2}{\frac {\theta }{2}}}}$	$S_{s}={\frac {\theta }{\sin \theta }}$	$S_{s}={\frac {1}{\cos {\frac {\theta }{2}}}}$	${\boldsymbol {S_{s}=1}}$
Skalierung (effektiv)	$S={\frac {1}{\sqrt {\cos ^{3}\theta }}}$	$S={\frac {1}{\cos ^{2}{\frac {\theta }{2}}}}$	$S={\sqrt {\frac {\theta }{\sin \theta }}}$	${\boldsymbol {S=1}}$	$S={\sqrt {\cos \theta }}$
Deformation	$D={\frac {1}{\cos \theta }}$	${\boldsymbol {D=1}}$	$D={\frac {\sin \theta }{\theta }}$	$D=\cos ^{2}{\frac {\theta }{2}}$	$D=\cos \theta$
Bildwinkel ${\boldsymbol {\alpha _{\text{max}}}}$	< 180°	< 360°	360° (und mehr)	360°	180°
$\alpha _{\text{stark}}$	102° ¹⁾	180° ¹⁾	217° ²⁾	180° ²⁾	120° ²⁾
$\alpha _{\text{mittel}}$	75° ¹⁾	131° ¹⁾	159° ²⁾	131° ²⁾	90° ²⁾
$\alpha _{\text{schwach}}$	54° ¹⁾	94° ¹⁾	115° ²⁾	94° ²⁾	66° ²⁾
Bildkreis ${\boldsymbol {\alpha }}$ = 180°	$\varnothing \infty$	$\varnothing 4f$	$\varnothing \pi f$	$\varnothing {\sqrt {8}}f$	$\varnothing 2f$
$\alpha$ = 360°		$\varnothing \infty$	$\varnothing 2\pi f$	$\varnothing 4f$
Fläche vorn : hinten		$1:\infty$	$1:3$	$1:1$

¹⁾ begrenzt durch Skalierung S
²⁾ begrenzt durch Deformation D

Die Skizze in der Tabelle ist so zu verstehen, dass die Szene erst auf eine Kugeloberfläche projiziert wird, mit der Kugelmitte als Projektionszentrum, um dann wie dargestellt von der Kugel auf die Bildebene abgebildet zu werden.

$\alpha _{\text{stark}}$ , $\alpha _{\text{mittel}}$ und $\alpha _{\text{schwach}}$ sind Beispiel-Bildwinkel. Mit stark, mittel und schwach ist die Stärke der Verzerrung durch die Skalierung $S$ und die Deformation $D$ gemeint. Sie liegt innerhalb folgender willkürlich gewählter Bereiche:

stark		$0{,}5\dotsc 2$
mittel		${\sqrt {0{,}5}}\dotsc {\sqrt {2}}$
schwach		${\sqrt[{4}]{0{,}5}}\dotsc {\sqrt[{4}]{2}}$

In der Bildmitte ist der betreffende Wert 1 (verzerrungsfrei) und wird zum Rand je nach Projektionstyp und Kenngröße stetig kleiner oder größer. Noch größere Bildwinkel sind mit einer fundamentalen Zwischenfunktion möglich (Abschnitt Mathematische Modelle weiter unten). Bei der gnomonischen Projektion passen diese Bereiche gut zur Einteilung in Superweitwinkel, gemäßigtes Weitwinkel und Normalobjektiv.

Parametrische Abbildungen

Handelsübliche Fischaugen werden nicht für Messzwecke, sondern für Fotografen entwickelt. Im oberen Kennlinienbereich sind einige Prozent Abweichung zu den fundamentalen Grundfunktionen möglich, um den Aufwand und damit Gewicht und Preis zu begrenzen. Eine bessere Annäherung an die reale Kennlinie kann mit Modellen erreicht werden, die auch Zwischen- und Spezialfunktionen über ein oder mehrere Parameter ermöglichen.

Bei den meist nicht-fundamentalen Abbildungen ist $N$ (siehe Kapitel Parameter) nicht allein von entsprechenden Parametern abhängig, sondern auch von $\theta$ . Die Umrechnung der Parameter nach $N$ zu Vergleichszwecken erfolgen dann für $\theta =0$ und ergibt $N_{0}=N(\theta =0)$ . Die nicht-fundamentale Funktion entspricht bei kleineren $\theta$ -Werten der entsprechenden fundamentalen Zwischenfunktion und nimmt bei größeren $\theta$ -Werten einen anderen Verlauf.

Tabelle 2: Parametrische Funktionen
Abbildungstyp (parametrisch)	allgemeine fundamentale Funktion	Beispiele für nichtfundamentale Funktionen
Abbildungstyp (parametrisch)	allgemeine fundamentale Funktion	Polynom	winkelskaliert	verschobenes Projektionszentrum	Fisch-Sicht (Kapitel Unterwasserblick)
Skizze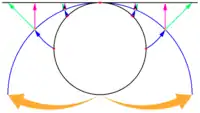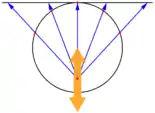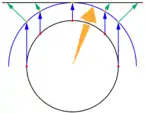
Parameter	$N$	$a_{3}...a_{2i+1}$	$L$	$Z$	Brechungsindex $n$
$N$	${\color {Gray}N}$	${\color {Gray}{\frac {\ln {S_{m}}}{\ln {S_{s}}}}}$
$N_{0}=N(\theta {\to }0)$	${\color {Gray}N}$	${\frac {18a_{3}}{6a_{3}+1}}$	${\frac {L\max(6L,-3L)}{L\max(2L,-L)+1}}$	$Z+2$	$3-n^{2}$
$B$	${\color {Gray}{\frac {2N-2}{N+1}}}$	${\color {Gray}{\frac {\ln D}{\ln S}}}$
$B_{0}=B(\theta {\to }0)$	${\color {Gray}{\frac {2N-2}{N+1}}}$	${\frac {24a_{3}-2}{24a_{3}+1}}$	${\frac {L\max(8L,-4L)-2}{L\max(8L,-4L)+1}}$	${\frac {2(Z+1)}{Z+3}}$	${\frac {4-2n^{2}}{4-n^{2}}}$
$C$	${\color {Gray}{\frac {N-2}{3-N}}}$	${\frac {6a_{3}-2}{3}}$	${\frac {L\max(2L,-L)-2}{3}}$	${\frac {Z}{1-Z}}$	${\frac {1-n^{2}}{n^{2}}}$
Abbildungsfunktion	… entwickelt aus ${\boldsymbol {{\frac {\mathrm {d} r}{\mathrm {d} \theta }}=\left({\frac {r}{\sin \theta }}\right)^{N}}}$ mit ${\tfrac {\mathrm {d} r}{\mathrm {d} \theta }}$ = f bei θ = 0 und r = 0	${\boldsymbol {r=f\cdot \sum _{i=0}^{n-1}a_{2i+1}\,\theta ^{2i+1}}}$ mit a₁ = 1	${\boldsymbol {r=f\,{\frac {\sin(L\,\theta )}{L\,\cos(\max(L,0)\cdot \theta )}}}}$	${\boldsymbol {r=f\,{\frac {(1-Z)\sin \,\theta }{\cos \,\theta -Z}}}}$	${\boldsymbol {r=f{\frac {\sin \theta }{\sqrt {1-{\frac {\sin ^{2}\theta }{n^{2}}}}}}}}$
meridionale Skalierung	${\color {Gray}S_{m}={\frac {\mathrm {d} r}{f\mathrm {d} \theta }}}$	$S_{m}=\sum _{i=0}^{n-1}(2i+1)\,a_{2i+1}\,\theta ^{2i}$	$S_{m}={\frac {\cos(\min(0,L)\cdot \theta )}{\cos ^{2}(\max(L,0)\cdot \theta )}}$	$S_{m}={\frac {(1-Z)(1-Z\cos \theta )}{(\cos \theta -Z)^{2}}}$	$S_{m}={\frac {\cos \theta }{(1-{\frac {\sin ^{2}\theta }{n^{2}}})^{1{,}5}}}$
sagittale Skalierung	${\color {Gray}S_{s}={\frac {r}{f\sin \theta }}}$		$S_{s}={\frac {\sin(L\theta )}{L\sin \theta \cos(\max(L,0)\cdot \theta )}}$	$S_{s}={\frac {1-Z}{\cos \theta -Z}}$	$S_{s}={\frac {1}{\sqrt {1-{\frac {\sin ^{2}\theta }{n^{2}}}}}}$
Skalierung (effektiv)	${\color {Gray}S={\sqrt {S_{m}\cdot S_{s}}}}$		$S={\sqrt {\frac {\sin(L\theta )\cos(\min(0,L)\cdot \theta )}{L\sin \theta \cos ^{3}(\max(L,0)\cdot \theta )}}}$	$S=(1-Z){\sqrt {\frac {1-Z\cos \theta }{(\cos \theta -Z)^{3}}}}$	$S={\frac {\sqrt {\cos \theta }}{1-{\frac {\sin ^{2}\theta }{n^{2}}}}}$
Deformation	${\color {Gray}D={\frac {S_{m}}{S_{s}}}}$		$D={\frac {L\sin \theta \cos(\min(0,L)\cdot \theta )}{\sin(L\theta )\cos ^{2}(\max(L,0)\cdot \theta )}}$	$D={\frac {1-Z\cos \theta }{\cos \theta -Z}}$	$D={\frac {\cos \theta }{1-{\frac {\sin ^{2}\theta }{n^{2}}}}}$
Bildwinkel ${\boldsymbol {\alpha _{\text{max}}}}$			${\frac {180^{\circ }}{\|L\|}}$	$2\arccos {\frac {Z}{\max(1,Z^{2})}}$	$180^{\circ }$ bei $n>1$
$\alpha _{\text{stark}}$	245° bei N = ${\tfrac {1}{3}}$		244° bei L = 0,2684	236° bei Z = −1,2734
$\alpha _{\text{mittel}}$	182° bei N = ${\tfrac {1}{3}}$		181° bei L = 0,2587	178° bei Z = −1,43
$\alpha _{\text{schwach}}$	132° bei N = ${\tfrac {1}{3}}$		131° bei L = 0,2542	130° bei Z = −1,536

grauer Text: allgemeingültige Formel, wenn es keine spezielle Formel gibt
Einige Formeln können Sonderfälle, wie z. B. L = 0, nicht berechnen. Die Sonderfall-Formeln sind im Interesse der Übersichtlichkeit nicht aufgenommen worden. Mit der max-und-min-Funktion werden mehrere parameterbereichabhängige Formeln zu einer vereint.

$\alpha _{\text{stark}}$ , $\alpha _{\text{mittel}}$ und $\alpha _{\text{schwach}}$ sind die Bildwinkel für $B(\theta ={\tfrac {\alpha }{2}})=-1$ , bei denen Skalierung $S$ und Deformation $D$ folgende willkürlich gewählte Werte haben:

stark	$D\approx 0{,}5$	$S\approx 2$
mittel	$D\approx {\sqrt {0{,}5}}$	$S\approx {\sqrt {2}}$
schwach	$D\approx {\sqrt[{4}]{0{,}5}}$	$S\approx {\sqrt[{4}]{2}}$

Mathematische Modelle

fundamentale Zwischenfunktion

Für fundamentale Funktionen bleibt die Balance zwischen Deformation und Skalierung unabhängig von

\theta

. Das Gleiche gilt auch für

N

, so dass

N

zum Parameter wird und beliebige Zwischenfunktionen bilden kann. Basierend auf

S_{m}=S_{s}^{N}

ergibt sich das Richtungsfeld (gewöhnliche Differentialgleichung)

{\frac {\mathrm {d} r}{\mathrm {d} \theta }}=\left({\frac {r}{\sin \theta }}\right)^{N}

.

Für

\theta \to 0

wird die Anfangsbedingung

{\frac {\mathrm {d} r}{\mathrm {d} \theta }}=f

festgelegt, die die Feldlinie der gewünschten Funktion selektiert. Über ein numerisches Verfahren kann die Funktionskurve der Abbildungsfunktion entwickelt werden. Mit dem Parameter

N

kann jede fundamentale Zwischenfunktion gebildet werden, außer mit N = 3 und N =

\infty

. Damit sind auch alle fundamentalen Grundfunktionen mit Ausnahme der orthografischen eingeschlossen. Die Berechnung ist aufwendig.

Bei gleichzeitiger Grenzwertigkeit von Deformation und Skalierung (

B=-1

,

N={\tfrac {1}{3}}

,

C=-{\tfrac {5}{8}}

) bekommt man die größtmöglichen Bildwinkel

\alpha _{\text{stark}}

,

\alpha _{\text{mittel}}

und

\alpha _{\text{schwach}}

(Werte siehe Tabelle 2). Der andere Fall gleichzeitiger Grenzwertigkeit

B=1

ist unbrauchbar (

C=\infty

,

\alpha _{\text{max}}=

0°).

skalierte Winkelfunktion

Bei einigen fundamentalen Funktionen haben die Winkelfunktion einen Faktor 0,5 oder 1 vor dem Winkel

\theta

. Mit diesem Faktor als Parameter

L

(Linearitätsfaktor, eigentlich Nichtlinearität) lassen sich die Tangens- und Sinusfunktionen skalieren.[14] Das Vorzeichen wählt zwischen Tangens und Sinus.

positive L:

r=f\,{\frac {\tan(L\,\theta )}{L}}

mit L= +

{\sqrt {\tfrac {N_{0}}{6-2\,N_{0}}}}

für 0<N₀<3

negative L:

r=f\,{\frac {\sin(L\,\theta )}{L}}

mit L= –

{\sqrt {\tfrac {N_{0}}{N_{0}-3}}}

für entweder N₀<0 oder N₀>3

Die beiden Fälle können mit der max-Funktion zu einer Formel zusammengefasst werden:

L\neq 0

:

r=f\,{\frac {\sin(L\,\theta )}{L\,\cos(\max(L,0)\cdot \theta )}}

mit weiterhin N₀-abhängig getrennter L-Berechnung wie oben.

L = 0 erfordert eine Sonderbehandlung mit

r=f\,\theta

. Somit sind alle fundamentalen Grundfunktionen eingeschlossen.

Das Thoby-Fisheye[15] ist auch eine skalierte Winkelfunktion und berechnet sich folgendermaßen:

r=k_{1}\,f_{\text{Nenn}}\sin(k_{2}\,\theta )

.

Für das AF DX Fisheye-Nikkor 10.5mm f/2.8G ED (

f_{\text{Nenn}}=10{,}5\,\mathrm {mm}

) wurden die Werte

k_{1}=1{,}47

und

k_{2}=0{,}731

empirisch gefunden.

k_{1}

müsste eigentlich

{\tfrac {1}{k}}_{2}

sein, wenn statt der auf dem Objektiv aufgedruckten Nennbrennweite die zu

k_{2}

passendste Brennweite verwendet wird. Dann lässt sich die weiter oben angegebene, allgemeine Formel mit

f=k_{1}k_{2}f_{\text{Nenn}}\approx

11.28 mm und

L

= - 0,731 anwenden. Die geringe Abweichung von

k_{1}

zu

{\tfrac {1}{k}}_{2}

, bzw.

f

zu

f_{\text{Nenn}}

deutet auf eine Skalierte Funktion (siehe weiter unten) hin.

Polynom

Abbildungsfunktionen sind zentralsymmetrisch und somit ungerade:

r=f\cdot \sum _{i=0}^{n-1}a_{2i+1}\,\theta ^{2i+1}

mit

a_{1}

=1 ,

a_{3}

=

{\tfrac {N_{0}}{18-6N_{0}}}

und weiteren ungeraden Gliedern.

n\,

ist die Anzahl der Polynomglieder. Parameter sind

a_{3}

,

a_{5}

…

a_{2n-1}

(

a_{1}

ist konstant). Für eine gute Nachbildung einer Optik sind mehrere Glieder und damit Parameter notwendig.

Aus Einfallswinkel-Bildradius-Punkten lässt sich ein Polynom berechnen, das so viele Koeffizienten hat, wie Punkte vorliegen. Aus einer analytischen Funktion lässt sich eine unendliche Polynomreihe herleiten, aber die vorliegenden Punkte weichen immer ein wenig von einer analytischen Funktion ab. Dadurch wird das Polynom mit steigender Punktzahl immer welliger. Es besteht die Gefahr einer oszillierenden Kurve mit riesigen Wellenbergen und -tälern zwischen den genau gebildeten Punktwerten.

Eine Spline-Interpolation, basierend auf niedergradigen Polynomstücken, führt zu einer besseren aber komplizierteren Lösung. Mit auf der Spline platzierten Stützstellen, die von Tschebyschow-Punkten abgeleitet sind, lässt sich ein annähernd fehleroptimiertes Polynom erzeugen. Die Stützstellen liegen (wegen des ungeraden Polynoms in

\theta ^{2}

-Skalierung) an den Bereichsgrenzen sehr eng zusammen und in der Mitte weiter auseinander, so dass die flachen Wellen in der Mitte und die steilen Wellen am Rand gleich hoch sind. Unter Umständen kann dann noch ein Nachjustieren der Stützstellen erforderlich sein, um dieses Optimum zu erreichen. Der Polynomgrad sollte nur so hoch sein, wie es die Genauigkeit (z. B. Bildpixelgröße) erfordert.

Geometrische Modelle

verschobenes Projektionszentrum

Diese Funktion beruht auf der Projektion einer Umgebungskugel auf eine Bildebene von einem Projektionszentrum, das von der Mitte der Umgebungskugel längs der optischen Achse verschoben ist. Mit der z-Achse als optische Achse wird der z-Wert des Projektionszentrums zum Parameter Z.

r=f\,{\frac {(1-Z)\sin \,\theta }{\cos \,\theta -Z}}

mit Z = N₀ – 2

Diese Funktion schließt folgende fundamentale Grundfunktionen ein: gnomonisch, winkeltreu, orthografisch. Auch wenn die Funktionen „äquidistant“ und „flächentreu“ nur näherungsweise erreicht werden können, passt das Modell gut. Bei diesem Modell werden die Randbereiche stärker komprimiert. Das ist meist auch bei realen Objektiven so.

Die Allgemeine Paniniprojektion benutzt in der Horizontalen diese Methode, aber die Formel enthält den Parameter d (Distanz, Z = − d).[9] Der Panoramaviewer "krpano" ermöglicht einen Fischaugeeffekt durch Überblendung von geradlinig (gnomonisch) nach fischaugenverzerrt mit Hilfe des Parameters view.distortion (Verzerrung, Z = − view.distortion).[16] Und auch die Raumverzerrung bei fast lichtschneller Bewegung lässt sich mit dieser Formel beschreiben (

Z=-{\tfrac {v}{c}}

).

Konstruktive Modelle

Optikrechnung

Wenn der Aufbau des optischen Systems bekannt ist, lässt sich der Verlauf von Lichtstrahlen berechnen. Parameter sind hier die Abfolge von Linsenflächen (Scheitelposition, Krümmungsradius und Brechungsindex des nachfolgenden Mediums), sowie die Lage von Aperturblende und Bildebene. Es ist sicherzustellen, dass der Strahl durch das Zentrum der Aperturblende geht. Für jeden Einfallswinkel oder bei Rückwärtsrechnung für jeden Bildpunkt ist der Strahlverlauf durch das optische System zu berechnen. Aus Einfallswinkel und Bildebenen-Auftreffpunkt ergibt sich die Abbildungsfunktion. Im Vergleich zu den anderen Abbildungsfunktionen sind statt eines Rechenschritts mehrere Rechenschritte entsprechend der Anzahl der Grenzflächen erforderlich. Dennoch ist die Rechnung noch relativ einfach, da im Gegensatz zur Optikentwicklung keine Rechnung mit breiten Strahlbündeln oder Wellenfronten, meridionalen und sagittalen Bildschalen oder Aberrationen notwendig ist.

Interpolationskurve

Basierend auf der Optikrechnung, wird eine Tabelle mit einer ausreichenden Anzahl von Einfallswinkel-Bildradius-Paaren erstellt. Diese Paare bilden eine Reihe von Punkten, die mit einer Spline-Interpolation durch Polynomstücke verbunden werden. Damit sinkt der Rechenaufwand gegenüber der reinen Optikrechnung. Einige Hersteller veröffentlichen solche Tabellen.[5]

Korrigierende Modelle

Abweichungspolynom

Statt mit einem hochgradigen Polynom ein Fischaugenobjektiv sehr genau zu simulieren, ist es günstiger, die Optik mit einem einfachen Modell anzunähern. Die noch verbleibende Abweichung der realen Optik gegenüber dem Modell beschreibt ein Polynom:

r=f\,\sum _{i=0}^{n-1}a_{2i+1}\left({\frac {r_{\rm {Modell}}}{f}}\right)^{2i+1}

(

n\,

ungerade Glieder)

Parameter sind

a_{1}=1

,

a_{3}={\frac {N_{0}}{18-6\,N_{0}}}-{\frac {N_{0,{\rm {Modell}}}}{18-6\,N_{0,{\rm {Modell}}}}}

und weitere Koeffizienten bis

a_{2n-1}

. Die Modellfunktion muss innerhalb des gesamten Bildfeldes eineindeutig (eine Bijektive Funktion) sein. Als Modellfunktion eignet sich die ähnlichste fundamentale Abbildung oder eine parametrische Abbildung mit nur einem, aber passend gewähltem Parameter. Das Abweichungspolynom ist dann weniger aufwendig. Wenn die Modellfunktion im paraxillaren Bereich mit der echten Optik gut übereinstimmt, wird

a_{3}=0

. Jedoch hat die Eineindeutigkeit der Modellfunktion absoluten Vorrang gegenüber der paraxillaren Übereinstimmung.

Sonderfall: Wenn die Modellfunktion winkellinear (äquidistant) ist, haben Polynom und Abweichungspolynom die gleichen Koeffizienten.

Separate Abweichungspolynome für Rot, Grün und Blau können die Farbquerfehler der Optik erfassen. Dafür werden meist

a_{1}

oder/und

a_{3}

der einzelnen Farbkanäle leicht gegeneinander variiert. Manchmal beschränkt man sich nur auf die Farbfehlererfassung und ignoriert die allgemeine Abweichung, wenn z. B. keine Panoramen erstellt werden sollen.

Zum Abweichungspolynom invers ist das Korrekturpolynom

r_{\rm {Modell}}=f\,\sum _{i=0}^{n-1}b_{2i+1}\left({\frac {r}{f}}\right)^{2i+1}

(

n\,

ungerade Glieder).

Für

a_{1}\approx 1

und bei den folgenden Gliedern

|a_{2i+1}|\ll 1

(

i\geqq 1

) lässt sich das Korrekturpolynom mit

b_{1}={\frac {1}{a_{1}}}

und

b_{2i+1}=-a_{2i+1}

(

i\geqq 1

) hinreichend genau erzeugen. Mit dem Korrekturpolynom kann das Bild in die gewählte Modellfunktion umgerechnet und im Farbquerfehler reduziert werden – meist als erste Stufe zur Umrechnung in einen anderen Projektionstyp.

Skalierte Funktion

Manchmal stehen nur wenige nicht ganz passende Abbildungsfunktionen zur Verfügung. Meist weichen sie einseitig ab. Mit einer abweichenden Brennweite

f_{\text{adapted}}

kann eine Abbildungsfunktion so optimiert werden, dass die tatsächliche Abbildungsfunktion gekreuzt wird und die Abweichungen beiderseits gleich und damit möglichst klein sind. Die Brennweite

f_{\text{adapted}}

wird zum Parameter. Voraussetzung ist, dass die tatsächliche Funktion wenigstens mit einigen Punkten bekannt ist. Durch die veränderte Brennweite werden Mittendetails in der Größe falsch interpretiert (stört meistens nicht).

Scheinfunktion

Manchmal stehen nur wenige nicht ganz passende nichtparametrische Abbildungsfunktionen zur Verfügung. Für diese kann die Brennweite

f_{\text{pseudo}}

so optimiert werden, dass sich bestimmte transformierte Bildeigenschaften verbessern.

Beispielsweise wird man für die flächentreue Abbildung die Brennweite solange variieren, bis z. B. eine gnomonische Umrechnung gerade Kanten ergibt – nachfolgend als Geraderechnen bezeichnet. Wird die umgerechnete Linie wellig, kann man auch probeweise die orthografische, winkellineare und winkeltreue Abbildung optimieren und sich für die Abbildungsfunktion entscheiden, die beim Geraderechnen die geringste Welligkeit hervorruft. Statt auf Geradlinigkeit kann man z. B. auch auf Deformationsfreiheit durch winkeltreue Umrechnung optimieren.

f_{\text{pseudo}}

hat dann einen anderen Wert. Das Geraderechnen ist jedoch die einfachere und sehr feinfühlige Methode, womit

f_{\text{pseudo}}

auf Prozentbruchteile genau bestimmt werden kann (durch Vergleich mit einer eingezeichneten Linie).

Das Geraderechnen ermöglicht eine nahezu perfekte gnomonische Umrechnung. Mit der gleichen Brennweite in die winkeltreue Abbildung umzurechnen führt zu einem geringen, aber bemerkbaren Fehler. Beim Versuch, Panoramen zu erstellen, gibt es schon größere Probleme. Grund dafür ist, dass im Gegensatz zu einer skalierten Funktion keine Anpassung an die wahre Abbildungsfunktionskurve erfolgt und durch die falsche Brennweite auch die Winkel der Objekte falsch interpretiert werden.

Durch ein Foto einer Testanordnung mit bekanntem objektseitigen Winkel können die wahre Brennweite

f

und die wahre Abbildungsfunktion bestimmt werden. Dazu muss aber auch der falsche Winkel

\theta _{\text{pseudo}}

über die inverse Schein-Abbildungsfunktion aus dem Bild berechnet werden.

In der gnomonischen Umrechnung gilt:

r=f\tan \theta =f_{\text{pseudo}}\tan \theta _{\text{pseudo}}

Damit kann die wahre Brennweite bestimmt werden:

f=f_{\text{pseudo}}{\frac {\tan \theta _{\text{pseudo}}}{\tan \theta }}

Wir definieren einen Korrekturfaktor

k={\frac {f}{f_{\text{pseudo}}}}={\frac {\tan \theta _{\text{pseudo}}}{\tan \theta }}

,

der zum Parameter wird, um die wahre Brennweite benutzen zu können.

Mit den normierten Abbildungsfunktionen

\mathbf {h_{\text{pseudo}}}

und

\mathbf {h}

können die scheinbare und die wahre Abbildungsfunktion verglichen werden.

r=f\,\mathbf {h} (\theta )=f_{\text{pseudo}}\mathbf {h_{\text{pseudo}}} (\theta _{\text{pseudo}})={\frac {f}{k}}\mathbf {h_{\text{pseudo}}} (\arctan(k\tan \theta ))

(Methode Geraderechnen)

Kernstück der Korrektur ist

\theta _{\text{pseudo}}=\arctan(k\tan \theta )

. Damit wird die Winkelkennlinie wellenförmig verbogen, wobei die Werte für 0°, 90° und 180° bestehen bleiben. Das ist eine ganz spezielle Korrektur, die nicht jede parametrische Abbildungsfunktionen leisten kann.

Eine Scheinfunktion nimmt durch eine falsche Brennweiteneingabe eine versteckte Korrektur vor. Es funktioniert nur die Umrechnung, für die die Scheinfunktion optimiert wurde. Das Herauslösen der wahren Korrektur ermöglicht eine neue parametrische Abbildungsfunktion, die für alle Umrechnungen funktioniert.

Beispiele für gerade-gerechnete Scheinfunktionen (links Scheinfunktion, rechts aufgelöst zur wahren Funktion):

r=2\,f_{\text{pseudo}}\sin \left({\frac {\theta _{\text{pseudo}}}{2}}\right)={\frac {2\,f}{k}}\sin \left({\frac {\arctan(k\tan \theta )}{2}}\right)

scheinbar flächentreu

r=f_{\text{pseudo}}\,\theta _{\text{pseudo}}={\frac {f}{k}}\arctan(k\tan \theta )

scheinbar äquidistant

Die Auswirkungen einer falschen Brennweite zeigen, dass es für alle anderen Funktionen wichtig ist, die wahren Winkel und Brennweiten zu bestimmen. Dazu ist ein Foto einer Testanordnung unumgänglich. Mit der wahren Brennweite gibt es weniger Probleme beim Umrechnen. Die aufgelösten Scheinfunktionen (mit den substituierten Ausdrücken für wahre Winkel und Brennweiten) können problemlos verwendet werden und werden durch k parametrisch. Bereits parametrische Funktionen können ebenso mit dem Parameter k aufgerüstet werden, um die Funktionskurve noch besser an die reale Optik anzupassen.

Hinweise

Abbildungsfunktionen realer Fischaugen weichen von den fundamentalen Grundfunktionen mehr oder weniger ab. Bei hohen Anforderungen an die Genauigkeit sind parametrische Funktionen anzuwenden. Die Funktion „verschobenes Projektionszentrum“ ist recht gut geeignet. Ansonsten kann man sich auch mit Scheinfunktionen behelfen.

Die Abbildungsfunktionen müssen im deformationsfreien Zentrum der Abbildung (der Bildpunkt in dem weder horizontale noch vertikale Linien gebogen werden) ihre Nullstelle haben. Dieser Punkt liegt versetzt zur Bildmitte und bei realen Objektiven auch nicht genau auf der optischen Achse des Fischauges oder genau auf der Mitte des Bildkreises eines Zirkularfischauges. Wird dieser Versatz beim Geraderechnen nicht berücksichtigt, sind alle Linien in die gleiche Richtung gebogen. Testaufnahmen im Quer- und Hochformat mit Linien am oberen und unteren Rand können helfen, mit Rechenversuchen den senkrechten und seitlichen Versatz zwischen deformationsfreiem Zentrum und Bildmitte zu bestimmen. Bei normalen Ansprüchen kann die Mitte eines Bildkreises oder die Lage der optische Achse verwendet werden. Die Bildmitte ist durch den Sensoreinbau und die Lage des genutzten Anteils des Sensorbereichs gegenüber dem Bajonett verschoben und sollte nur bei geringen Ansprüchen verwendet werden.

Die Abbildungsfunktionen gelten nur für ausreichend weit entfernte Objekte. Die Eintrittspupille von Fischaugen ist nicht ortsfest, sondern wandert mit wachsendem Einfallswinkel auf einem Bogen nach vorn und zur Seite des einfallenden Strahls.[17] Für nahe Objekte kommt es zu einem Parallaxenfehler, sie werden von der verlagerten Eintrittspupille in einem größeren Einfallswinkel und kleinerem Abstand gesehen, als von der frontalen Eintrittspupille zu erwarten wäre. Nahe Objekte werden so radial zusätzlich gestreckt. Das kompensiert die Randstauchung der meisten Fischaugen mehr oder weniger. Die Abbildungsfunktion verändert sich abstandabhängig. Nahe gerade Kanten sind deshalb als Referenz zum Geraderechnen ungeeignet. Eine geeignete Referenz ist z. B. der Meereshorizont.

Bei den Umrechnungen wird oft vom Bild ausgehend, also rückwärts gerechnet. Dementsprechend sind inverse Abbildungsfunktionen zu verwenden. Bei der Rückwärtsrechnung wird anstelle des Einfallswinkels entweder direkt in eine Zielfunktion oder in einen 3D-Raumpunkt (Rückprojektion) umgerechnet.

Umwandlung

Wenn die für Fischaugenobjektive typischen Verzerrungen nicht als gestalterisches Element gewünscht sind, können digitale Fischaugen-Aufnahmen mit Hilfe von Bildverarbeitungsprogrammen entzerrt werden. Dies geht jedoch meist mit abnehmender Qualität zum Bildrand hin, oder mit einer Einschränkung des abgebildeten Sichtfeldes einher.

Es gibt unterschiedliche Projektionen,[18] in die ein Fischaugenbild umgewandelt werden kann:

azimutal ist eine Gruppe folgender Projektionen: gnomonisch, winkeltreu, winkellinear, flächentreu und orthografisch (Kapitel Fundamentale Abbildungen). Konventionelle Objektive und Fischaugenobjektive bilden idealerweise so ab. Parametrische azimutale Funktionen, wie skalierte Winkelfunktion und verschobenes Projektionszentrum, können Quelle einer Umrechnung sein, aber nicht ein erstrebenswertes Ziel.

Linien durch die Bildmitte (z. B. Fluchtlinien) bleiben gerade und in Originalrichtung. Zentrumskreise bleiben kreisförmig. Eine verkantete Aufnahme kann auch nach der Umrechnung ganz einfach durch eine Bildrotation korrigiert werden.

Würfelnetz: Der Spezialfall Kreuzform (Cubic cross)[19] ist die Abwicklung eines Umgebungswürfels und enthält aneinanderhängende gnomonische Projektionen.

An den Würfel-Faltkanten werden die Bild-Linien geknickt abgebildet. Andere Kanten müssen zum Abwickeln aufgeschnitten werden. Punkte beiderseits solcher Kanten schwenken auseinander und verlieren ihre Nachbarschaft. Der Spezialfall Kreuzform benötigt für die Darstellung der 6 Teilbilder eine Bildfläche von 4 × 3 Teilbildbreiten. Das hat den Nachteil, dass nur 50 % der Bildfläche genutzt werden.

Der Spezialfall Reihe hat sämtliche Teilbilder nebeneinander und ist keine Abwicklung. Das resultierende Bild hat ein Seitenverhältnis von 6:1 und besteht z. B. aus der Anordnung vorn-rechts-hinten-links-oben-unten. Die Bildfläche wird zu 100 % genutzt. Einige Panoramabetrachter erkennen auf Grund dieses Seitenverhältnisses die "Würfel-Projektion" und können sie zusätzlich zum Kugelpanorama (2:1) als Quelle nutzen.

Panorama ist eine Gruppe zylindrischer Projektionen, die auf eine Ebene abgewickelt werden. Mit üblicherweise senkrechter Zylinderachse ergibt sich eine horizontale winkellineare Teilung. In vertikaler Richtung (Achsrichtung) wird entsprechend einer Funktion, aber vom Umlaufwinkel unabhängig skaliert. Entsprechend dieser Skalierung gibt es folgende Panoramen: gnomonisch (Zylinderabwicklung), winkeltreu (Mercator), winkellinear (Kugelpanorama), flächentreu (Lambert).

Vertikale Linien in Achsrichtung bleiben gerade. Alle Richtungen um die Achse sind gleichberechtigt. Eine verkantete Aufnahme führt zu einem wellenförmigen Horizont und zu S-förmigen Vertikalen. Der maximal mögliche Bildwinkel ist 360° horizontal und 180° vertikal.

Transversale Panoramen funktionieren genauso, jedoch ist die Zylinderachse waagerecht, so dass horizontale Linien gerade bleiben. Der maximal mögliche Bildwinkel ist 180° horizontal und 360° vertikal.

Vielfach gnomonisches Panorama[20] (Multiple rectilinear panorama) nach Dersch ist eine Projektion auf eine prismatische Mantelfläche, die abgewickelt wird.

Wie beim Panorama sind auch hier die Vertikalen gerade. Horizontale Linien sind nicht mehr gekrümmt, sondern an den Kanten der Mantelfläche geknickt (evtl. mit Verrundung) und dazwischen gerade. Die Mantelfläche ist passend für jedes Bild einzurichten. Bei einer Häuserfront z. B. sind die Knickkanten auf die Grenzen zwischen den Einzelhäusern zu legen.

In Gegensatz zum Würfelnetz muss nichts aufgeschnitten werden.

Pannini-Projektion[9] (alternative Schreibweise: Panini-Projektion[8]) ist eine Zylinderprojektion, die nicht abgewickelt, sondern auf die Bildebene umprojiziert wird. In horizontaler Umlaufrichtung ist die Funktion analog einer azimutalen Projektion (winkeltreu, winkellinear, orthografisch, oder verschobenes Projektionszentrum). In vertikaler Achsrichtung ist die Projektion gnomonisch und zum seitlichen Winkel so skaliert, dass zentrale Fluchtlinien gerade sind und im Originalwinkel verlaufen.

Vertikale Linien in Achsrichtung und zentrale Fluchtlinien sind gerade. Eine verkantete Aufnahme verbiegt nicht zentrische Vertikalen S-förmig.

Bei sehr großem vertikalen Bildwinkel kann in vertikaler Achsrichtung die gnomonische durch die Mercatorprojektion ersetzt werden, um Verzerrungen zu mildern. Das ist dann keine echte Pannini-Projektion mehr und wird z. B. veduta mercator[18] genannt. Schräge Fluchtlinien sind dann auch leicht S-förmig.

Rundrechteck-Projektion[21] nach Chang, Hu, Cheng, Chuang ist die Projektion eines vierkantigen Ellipsoids auf die Bildebene. Als Sonderfälle sind auch die azimutale Projektion und die Pannini-Projektion möglich.

Ein kreisförmiges 180° Bildfeld wird in ein Rechteck umgeformt, wobei die Ecken zur Vermeidung scharfkantiger Knicke verrundet werden. Die Rechteckdiagonalen teilen das Bildfeld in vier Dreiecke. Im oberen und unteren Dreieck werden horizontale Linien gerade. Im linken und rechten Dreieck werden vertikale Linien gerade. Es sind Bildwinkel von über 180° möglich.

Rechteck[18] nach Wieden ist die Überlagerung eines normalen und eines transversalen Panoramas.

Durch die Übernahme der x-Werte aus dem einen und der y-Werte aus dem anderen Panorama erreicht man sowohl gerade horizontale und gerade vertikale Linien unabhängig von der Lage im Bild. Schräge Linien verlaufen S-förmig und werden zum Bildrand in die 45° oder 135°-Richtung gebogen. Der Öffnungswinkel ist auf 180° begrenzt. Entsprechend der Panorama-Art kann die Rechteck-Projektion winkeltreu, winkellinear, oder flächentreu sein.

RectFish[22] ist eine Projektion, die ein oben und unten beschnittenes zirkulares Bildfeld in das Rechteck des Bildformates einpasst.

Es wird möglichst viel vom Originalbild behalten. Wie beim Panorama werden senkrechte Linien gerade. Die horizontale Teilung aber bleibt nichtlinear, und die radiale Randkompression bleibt auch.

Es sind gibt weitere Projektionen,[23] in die umgerechnet werden kann, z. B. die Quincunx-Kartenprojektion (Beispielfoto 360° in der englischen Ausgabe – abgerufen am 20. Dezember 2015). Je nach Motiv ist die eine oder die andere Projektion besser geeignet.

In schwierigen Fällen ist auch die Richtung der Kamera per Software zu ändern, um z. B. stürzende Linien zu korrigieren oder Verkantungen auszugleichen. Diese Korrektur erfolgt, indem das Bild über die Quell-Abbildungsfunktion in den 3D-Raum auf die Umgebungskugel oder eine Bildschale zurück projiziert wird, der Raum über eine Transformationsmatrix gedreht wird, und dann der gerade oder passend gedrehte Raum über die Ziel-Abbildungsfunktion wieder auf die Bildebene zurückgerechnet wird.

Anwendungen

Wissenschaftler und Ressourcen-Manager (z. B. Biologen, Förster, Geographen und Meteorologen) verwenden Fischaugenobjektive, um in der Ökophysiologie einen halbkugelförmigen Bereich der Pflanzenvegetation zu erfassen oder die potentielle kurzwellige Einstrahlung aus der Horizontüberhöhung (engl. sky view factor) sowie der daraus abzuleitenden langwelligen Ausstrahlung zu prognostizieren. Aus der Analyse dieser Bilder können relevante Strukturparameter von Baumkronen abgeleitet werden wie Blattflächenindex (LAI), Blattwinkelverteilung und bodennahe Lichtverfügbarkeit. Fischaugenobjektive helfen auch bei der Auswertung des Waldzustands, der Erfassung der Überwinterungsplätze von Monarchfaltern und der Verwaltung von Weinbergen. In der Topoklimatologie kann aus Horizontüberhöhung von Bodensenken die Entstehung von tiefen Frösten bei Inversionswetterlagen abgeleitet werden, sowie Aussagen über Ursachen von Kaltluftsee-Phänomenen gemacht werden (Funtensee).[24]
Aus Daten der aus georeferenzierten Fischaugenaufnahmen gewonnenen Parameter des sky view factors werden in der Stadtklimatologie meteorologische Zusammenhänge der Strahlungsbilanz städtischer Wärmeinseln untersucht.
Meteorologen bestimmen die Bewölkung (Bedeckungsgrad des Himmels).
Astronomen nehmen einen großen Teil des Himmels auf und erfassen damit Sternbilder, Milchstraße, Meteore, Polarlichter und die Lichtverschmutzung.
Viele Planetarien verwenden Fischaugen-Projektionsobjektive, um den Nachthimmel oder andere digitale Inhalte auf das Innere einer Kuppel zu projizieren.
Überwachungskameras mit Fischaugenobjektiv können einen ganzen Raum auf einmal erfassen. Im Gegensatz zu schwenkbaren Kameras gibt es keinen zeitweise toten Bereich und keinen anfälligen Antrieb.
Video-Türsprechanlagen mit besonders großem Bildwinkel (Türspion-Funktion).
Beim IMAX-Dome-System (zuvor 'OMNIMAX') erfolgt die Filmaufnahme durch ein Zirkular-Fischaugenobjektiv, und die Projektion des Kinofilms durch eine ähnliche Optik auf eine halbkugelförmige Leinwand.
Fotografen und Videofilmer verwenden Fischaugenobjektive um die Kamera für Action-Aufnahmen so nah wie möglich an die entscheidende Stelle zu bringen und dabei auch noch den Gesamtzusammenhang aufzunehmen. Zum Beispiel wird beim Skateboarden auf das Brett fokussiert, und der Skater ist trotzdem im Bild zu sehen.
Das erste Musikvideo, das vollständig mit einem Fischaugenobjektiv aufgenommen wurde, war der Song „Shake Your Rump“ von den Beastie Boys im Jahr 1989.
Flugsimulatoren und visuelle Gefechtsimulatoren verwenden Fischaugen-Projektionsobjektive um eine lückenlose Umgebung für Piloten, Fluglotsen oder militärisches Personal zum Trainieren zu erstellen
In der Computergrafik können Zirkular-Fischaugen verwendet werden, um ein Environment Mapping der physischen Welt zu erstellen. Ein komplettes 180-Grad-Fischaugenbild kann die Hälfte eines Kubischen Environment Mappings mit einem entsprechenden Algorithmus füllen. Environment Maps können verwendet werden, um 3D-Objekte eingebettet in virtuellen Panoramen wiederzugeben.
Kompakte digitale Panoramakameras sind meist mit zwei Miniatur-Fischaugenobjektiven und zwei Bildsensoren ausgestattet, die gleichzeitig ausgelöst werden. Die Kompaktbauweise sorgt für eine geringe Parallaxe, und der Bildwinkel von etwa 210° für eine Überlappungszone. Beides erleichtert das automatische Stitching.

Galerie

Beispielaufnahmen mit Fischaugenobjektiven
Weltraumaufnahme eines tropischen Wirbelsturms über den Bahamas.
Das Hauptschiff der Basilika Saint-Julien de Brioude in der Auvergne.
Luftaufnahme der Burg Diósgyőr in Ungarn.
Der Moul Wasserfall im Wells Gray Provincial Park (British Columbia, Kanada) aus der benachbarten Felshöhle aus gesehen.
Hemisphärische Aufnahme der Nachthimmels mit der Milchstraße im Sternenpark Westhavelland.
Riesen-Lebensbaum am Giant Cedar Trail im Mount-Revelstoke-Nationalpark (British Columbia, Kanada).

Alternativen

Linsensysteme

Fischaugen-Vorsatzobjektiv für Smartphone

Innenraum mit Smartphone und Fischaugen-Vorsatzoptik fotografiert

Um den Fischaugen-Effekt zu erzielen, sind auch spezielle Vorsätze erhältlich, die vorn auf ein normales Objektiv aufgeschraubt, aufgerastet, geklemmt (Klipps oder Klammer) oder (z. B. beim Smartphone) magnetisch angeheftet werden. Die Kombination aus normalem Objektiv und Vorsatz verhält sich dann wie ein Fischauge. Die Vorsätze gibt es als Vorsatzobjektiv und als Vorsatzlinse.

Vorsatzobjektiv

Ein Fischaugenvorsatz (Fischaugenkonverter) ist ein stark verkleinernder Weitwinkelkonverter mit tonnenförmiger Verzeichnung. Er besteht aus mehreren Linsen und funktioniert wie ein umgekehrt benutztes Galilei-Fernrohr. Die zur Abbildung nötige Brechkraft kommt ausschließlich vom nachfolgenden Objektiv.

Um den Verlust an Bildqualität gering zu halten, muss sich die Eintrittspupille des Objektivs in einem bestimmten Abstand zum Vorsatz befinden und darf nicht zu groß sein (abblenden). Nur bei einem bestimmten Abstand zwischen Vorsatz und Objektiv wird eine Bildposition durch die passend dazu korrigierte Stelle der Hinterlinse des Vorsatzes gesehen. Von der Eintrittspupille des Objektivs aus gesehen, sollte der Bildfeldrand genau auf den Hinterlinsenrand passen (gilt für Fischaugenvorsätze). Je nach Objektiv oder Smartphone ist der Abstand oft nicht optimal, und die Bildqualität verschlechtert sich dann erheblich. Neuere Smartphone-Kameras haben durch ihre lichtstärkeren Objektive eine größere Öffnung, die in Verbindung mit Vorsatzobjektiven auch zu schlechterer Bildqualität führt.

Zoomobjektive mit Fischaugenvorsatz können im gesamten Brennweitenbereich verwendet werden, wobei der Fischaugeneffekt in der Weitwinkelstellung sichtbar wird. Bei schlecht korrigierten Vorsätzen kann das Bild im stärkeren Telebereich unscharf sein.

Ein Türspion funktioniert ähnlich, jedoch übernimmt das Auge die Funktion des nachfolgenden Objektivs.

Vorsatzlinse

Eine speziell geformte Zerstreuungslinse, oft Semi-Fisheye genannt, erzeugt ein verkleinertes virtuelles Bild mit tonnenförmiger Verzeichnung. Durch die ziemlich plane Vorderseite wird der gesamte Bereich vor der Linse (180°-Bildwinkel) im Glas auf den zweifachen Winkel der optischen Totalreflexion (ca. 80°) gebrochen. Eine halbkugelförmige Vertiefung auf der Rückseite belässt oder verkleinert weiterhin diesen Bildwinkel beim Austritt aus dem Glas. Diese Linse hat eine negative Brennweite, und das nachfolgende Objektiv muss auf extreme Nahdistanz (wenige Zentimeter) fokussieren. Nicht jedes Objektiv kann das. Zoomobjektive können bestenfalls im Weitwinkelbereich so nah fokussieren. Vorsatzlinsen sind nicht zoomfähig. Die Qualität ist noch schlechter als bei einem Vorsatzobjektiv.

Spiegel

Spiegelbilder auf konvexen Spiegeln sind wie bei Fischaugenobjektiven tonnenförmig verzerrt. Aus großem Abstand betrachtet, erzeugt eine Spiegelkugel eine flächentreue (engl.: „equi-solid“) Abbildung. Die Rückseite eines Parabolspiegels erzeugt eine winkeltreue Abbildung. Mit entsprechenden Spiegelformen sind auch andere Abbildungsarten möglich. Wegen der Selbstabbildung der Fotoausrüstung ist nur eine ringförmige Zone nutzbar.

Vorteile: Es sind Bildwinkel über 180° problemlos möglich. Damit können 360°-Zylinderpanoramen aus einem Bild oder Video (bewegtes Panorama) erzeugt werden. Bei Videos ist es zeitlich nicht möglich, zwischen den Bildphasen mehrere Bilder zum späteren Zusammensetzen (dem sog. Stitching) zu machen.
Nachteile: Der Fotoapparat (evtl. auch Stativ und Fotograf) ist in der Mitte des Spiegelbildes zu sehen. Mit einem langbrennweitigen Makro- oder Teleobjektiv kann diese Fläche zwar klein gehalten, aber nicht vermieden werden, wenn man nur ein Einzelbild statt eines Panoramas anstrebt.; Der Bereich hinter dem Spiegel geht verloren. Das ist kein echter Nachteil, denn Linsen-Fischaugen können auch nicht ganz nach hinten sehen.; Spiegel-Fischaugen gibt es nicht auf dem freien Markt. Man muss durch Eigenbau passende Lösungen schaffen.

Es gibt aber auch fertig konfektionierte omnidirektionale Kameras mit katadioptrischem System. Dabei wird eine Linsenoptik mit einem Spiegel ergänzt. So entsteht ein abgestimmtes kompaktes System, das meist auch die Kamera mit einschließt. Für Panoramen sollte die Linsenoptik nach oben gerichtet sein, mit dem Spiegel darüber. Ein dünnwandiger Glaszylinder trägt den Spiegel (einzelne Spiegelstützen würden das Panorama unterbrechen). Das Ringpanorama kann in ein normales Panorama umgerechnet werden. Nadir (von der Linsenoptik verdeckt) und Zenit (vom Spiegel verdeckt) sind nicht abbildbar. Es sind auch mehrere Spiegel möglich, oder die Spiegelung erfolgt innerhalb eines Glaskörpers durch Totalreflexion oder Spiegelbeschichtung.

Unterwasserblick

Wasser ideal n = 1,33349

Wasser real n ist farbabhängig.

Wenn ein Fisch aus dem Wasser blickt, sieht er die Außenwelt verkleinert und tonnenförmig verzerrt. Die Außenwelt (180°) erscheint in einem Kegel mit einem Bildwinkel von 96° (doppelter Winkel der optischen Totalreflexion). Dieser Bereich wird auch snellsches Fenster[25] genannt. Außerhalb dieses Fensters spiegelt sich die Unterwasserwelt an der Wasseroberfläche durch Totalreflexion. Der gleiche Effekt tritt beim seitlichen Ausblick aus einem Aquarium mit planen Wänden auf.

Die Außenwelt erscheint in der Mitte auf 75 % verkleinert und am Rand komprimiert. Eine Tauchermaske oder ein Kamera-Unterwassergehäuse mit einer planen Sichtscheibe heben diesen Effekt wieder auf, da die Blickrichtung an der von der Sichtscheibe erzeugte Wasserebene gebrochen wird. Nur mit den direkt im Wasser befindlichen Augen oder aus dem Kugelmittelpunkt einer durchsichtigen Haube kann man ohne Richtungsverfälschungen ins Wasser sehen und so den Fischaugeneffekt wahrnehmen. Durch den Augapfel oder die Haube wird das Wasser zu einer Vorsatzlinse geformt (siehe oben unter „Linsensysteme“). Im Fall des Augen-Wasserkontakts kann man deshalb nicht scharf sehen. Außerdem verhindern Wellen auf der Wasseroberfläche einen klaren Ausblick.

Robert W. Wood, Professor für Experimentelle Physik, beschrieb diesen Effekt und baute eine Wassereimerkamera für den Blick nach oben und eine wassergefüllte Lochkamera für beliebige Blickrichtungen und machte damit die ersten Fischaugenfotos.[26][27] Das gab den später entwickelten Objektiven mit gleicher Sichtweise den Namen Fischaugenobjektiv.

Die Formel beschreibt die Abbildung einer Lochkamera, die mit einem optisch brechenden Medium gefüllt ist:

r=f{\frac {\sin \theta }{\sqrt {1-{\frac {\sin ^{2}\theta }{n^{2}}}}}}

r

Bildlage als Abstand zur Bildmitte

f

(zentrale) Brennweite, berücksichtigt auch die Verkleinerung

f={\frac {s}{n}}

s

Schnittweite, Abstand zwischen Aperturblende (Loch) und Bildebene

\theta

Polarwinkel des abzubildenden Außenobjekts

n

Brechungsindex des Mediums

Luft hat einen Brechungsindex nahe bei $n=1$ . In diesem Fall ist die Abbildung gnomonisch. Bei sehr großem Brechungsindex wird die Abbildung orthografisch. Die anderen Funktionen aus dem Kapitel „Abbildungsfunktionen“ können in der Bildmitte angenähert ( $n={\sqrt {3-N_{0}}}$ ), aber für große Winkel nicht nachgebildet werden. Für einen Brechungsindex größer als eins ist der Blickwinkel in die Außenwelt immer 180° und der Rand komprimiert.

Stitching

Fischaugen-Effekt mittels App

Panorama von Kamera mit zwei Fischaugen

Mehrere Aufnahmen vom gleichen Standpunkt können mit Stitching- oder Panoramasoftware zu einem Bild oder einem 360-Grad-Video zusammengesetzt werden. Hierzu gibt es auch Panoramakameras, die mit mehreren Objektiven und Bildsensoren ausgestattet sind, die gleichzeitig ausgelöst werden.

Die Software kann meist mehrere Projektionsarten ausgeben und so auch eine Fischaugenabbildung simulieren. Wenn die Software nur ein Panorama ausgeben kann, lässt sich dieses mit anderer Software in ein Fischaugenbild umrechnen.

Es gibt zum Beispiel auch Kamera-Apps für Smartphones, die den Fischaugen-Effekt als Variante des Panoramabilds erzeugen.

Weblinks

Commons: Fischaugen-Aufnahmen – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Fischaugenobjektiv – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Bebilderte Geschichte der Nikon Fischaugen-Objektive (deutsch)
Additional Information on Fisheye-Nikkor lenses (englisch)
Über Projektion und Verzeichnung (PDF; 949 kB) und über gestalterische Aspekte (PDF; 2,4 MB), zwei Grundlagenbeiträge über Fischaugen-Objektive
Fisheye in olypedia.de
Strahlengänge, Animationen (englisch), Original in französisch
Entaniya Fisheyes 200°/250° HAL – Abbildungsfunktion. fisheyelens.de, abgerufen am 15. Februar 2018. – Beispiel für Polynomberechnung

Einzelnachweise

Chadwick B. Martin: Design issues of a hyper-field fisheye lens. (PDF; 207 kB) University of Arizona, archiviert vom Original am 6. Juni 2014; abgerufen am 5. Juni 2014 (englisch).
Additional Information on 8mm f8 Fisheye-Nikkor Lens (englisch)
M.ZUIKO DIGITAL ED 8mm 1:1.8 Fisheye PRO – OM-D & PEN Objektive – Olympus. Abgerufen am 1. März 2017.
Entaniya Super Wide Fisheye Lens for P0.5/M12. Entaniya Co.,Ltd., abgerufen am 15. Februar 2018 (englisch).
HAL 250/200 - Entaniya. Entaniya Co.,Ltd., abgerufen am 15. Februar 2018 (englisch)., (Tabellen unter Technical Specification → MFT/Image Height: More Info, abgerufen am 2018-02-15)
Canon EF8-15mm f/4L Fisheye USM an Kamera mit Sensor im Kleinbildformat.
smc Pentax-DA FISH-EYE 10-17mm 1:3.5-4.5 ED für Kamera mit Cropsensor (Register Downloads für Beispielbilder).
Panini-Projektion (englisch).
Thomas K. Sharpless, Bruno Postle, Daniel M. German: Pannini: A New Projection for Rendering Wide Angle Perspective Images. (PDF 16,35 MB) Computational Aesthetics in Graphics, Visualization, and Imaging, 2010, abgerufen am 12. August 2014 (englisch).
Räumliche Motive, in: Wikibook Digitale bildgebende Verfahren – Bildaufnahme, abgerufen am 31. Dezember 2016
Samyang Fish-eye bei lenstip.com (englisch)
Samyang 8 mm f3.5 fisheye CS lens, Rasur und Testbericht (englisch).
Little planet in der englischen Wikipedia
D. B. Gennery: Generalized camera calibration including fish-eye lenses. (PDF 5,06 MB, Kapitel 2.3. „Basic Lens Model“, S. 12) Jet Propulsion Laboratory, 2003, abgerufen am 10. August 2014 (englisch).
Fisheye Projection. Abgerufen am 20. August 2014 (englisch).
krpano XML Reference bei krpano.com (englisch)
D. B. Gennery: Generalized camera calibration including fish-eye lenses. (PDF 5,06 MB, Kapitel 2.2. „Moving Entrance Pupil“, S. 7) Jet Propulsion Laboratory, 2003, abgerufen am 10. August 2014 (englisch).
Peter Wieden:Zimmer, abgerufen am 12. Dezember 2015.
Bredenfeld, Thomas: Digitale Fotopraxis Panoramafotografie. 2., aktualisierte und erweiterte Auflage. Galileo Press, Bonn 2012, ISBN 978-3-8362-1861-0, 5.12 Grundlegende Aufnahmebeispiele, S. 66.
H. Dersch: Multiple Rectilinear Panoramas. 2010, abgerufen am 23. Dezember 2015 (englisch).
Che-Han Chang, Min-Chun Hu, Wen-Huang Cheng, Yung-Yu Chuang: Rectangling Stereographic Projection for Wide-Angle Image Visualization. (PDF; 11,5 MB) 2013, abgerufen am 11. Dezember 2015 (englisch).
RectFish projection comparisons, abgerufen am 20. Dezember 2015.
John P. Snyder, Philip M. Voxland: An Album of Map Projections (Professional Paper 1453). (PDF; 12,6 MB, 249 Seiten) U.S. Geological Survey, 1989, abgerufen am 26. Dezember 2015 (englisch).
Geiger, R. Aron, R.H., Todhunter, P. 2009: The Climate Near the Grond. 7. Ausgabe, Rowman & Littlefield, London. ISBN 978-0-7425-5560-0. (Rudolf Geiger: Das Klima der bodennahen Luftschicht. Verlag F. Vieweg & Sohn Braunschweig 1927 = Die Wissenschaft Bd. 78; 2. Aufl. ebd. 1942; ab 3. Aufl. Titel mit dem Zusatz Handbuch der Mikroklimatologie ebd. 1950; 4. Aufl. ebd. 1961. 5. Aufl. unter dem Titel The Climate near the Ground herausgegeben von Robert H. Aron und Paul Todhunter. Verlag F. Vieweg & Sohn Braunschweig 1995).
Snell’s window in der englischen Wikipedia
R. W. Wood: Fish-Eye Views, and Vision under Water. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Band 12, Nummer 6. In: Taylor & Francis Online. Johns Hopkins University, August 1906, S. 159-161, abgerufen am 3. Juni 2019 (englisch).
Prof. R. W. Wood: Fischaugen-Sicht und das Sehen unter Wasser (Übersetzung). 1906, abgerufen am 25. August 2019.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Chadwick B. Martin: Design issues of a hyper-field fisheye lens. (PDF; 207 kB) University of Arizona, archiviert vom Original am 6. Juni 2014; abgerufen am 5. Juni 2014 (englisch).

[2] Additional Information on 8mm f8 Fisheye-Nikkor Lens (englisch)

[3] M.ZUIKO DIGITAL ED 8mm 1:1.8 Fisheye PRO – OM-D & PEN Objektive – Olympus. Abgerufen am 1. März 2017.

[4] Entaniya Super Wide Fisheye Lens for P0.5/M12. Entaniya Co.,Ltd., abgerufen am 15. Februar 2018 (englisch).

[entaniyaHAL-5] HAL 250/200 - Entaniya. Entaniya Co.,Ltd., abgerufen am 15. Februar 2018 (englisch)., (Tabellen unter Technical Specification → MFT/Image Height: More Info, abgerufen am 2018-02-15)

[6] Canon EF8-15mm f/4L Fisheye USM an Kamera mit Sensor im Kleinbildformat.

[7] smc Pentax-DA FISH-EYE 10-17mm 1:3.5-4.5 ED für Kamera mit Cropsensor (Register Downloads für Beispielbilder).

[huginpanini-8] Panini-Projektion (englisch).

[tksharpless-9] Thomas K. Sharpless, Bruno Postle, Daniel M. German: Pannini: A New Projection for Rendering Wide Angle Perspective Images. (PDF 16,35 MB) Computational Aesthetics in Graphics, Visualization, and Imaging, 2010, abgerufen am 12. August 2014 (englisch).

[digBildgebend-10] Räumliche Motive, in: Wikibook Digitale bildgebende Verfahren – Bildaufnahme, abgerufen am 31. Dezember 2016

[11] Samyang Fish-eye bei lenstip.com (englisch)

[12] Samyang 8 mm f3.5 fisheye CS lens, Rasur und Testbericht (englisch).

[13] Little planet in der englischen Wikipedia

[14] D. B. Gennery: Generalized camera calibration including fish-eye lenses. (PDF 5,06 MB, Kapitel 2.3. „Basic Lens Model“, S. 12) Jet Propulsion Laboratory, 2003, abgerufen am 10. August 2014 (englisch).

[15] Fisheye Projection. Abgerufen am 20. August 2014 (englisch).

[16] rpano XML Reference bei krpano.com (englisch)

[17] D. B. Gennery: Generalized camera calibration including fish-eye lenses. (PDF 5,06 MB, Kapitel 2.2. „Moving Entrance Pupil“, S. 7) Jet Propulsion Laboratory, 2003, abgerufen am 10. August 2014 (englisch).

[felRoom-18] Peter Wieden:Zimmer, abgerufen am 12. Dezember 2015.

[19] Bredenfeld, Thomas: Digitale Fotopraxis Panoramafotografie. 2., aktualisierte und erweiterte Auflage. Galileo Press, Bonn 2012, ISBN 978-3-8362-1861-0, 5.12 Grundlegende Aufnahmebeispiele, S. 66.

[20] H. Dersch: Multiple Rectilinear Panoramas. 2010, abgerufen am 23. Dezember 2015 (englisch).

[changRSP-21] Che-Han Chang, Min-Chun Hu, Wen-Huang Cheng, Yung-Yu Chuang: Rectangling Stereographic Projection for Wide-Angle Image Visualization. (PDF; 11,5 MB) 2013, abgerufen am 11. Dezember 2015 (englisch).

[22] RectFish projection comparisons, abgerufen am 20. Dezember 2015.

[23] John P. Snyder, Philip M. Voxland: An Album of Map Projections (Professional Paper 1453). (PDF; 12,6 MB, 249 Seiten) U.S. Geological Survey, 1989, abgerufen am 26. Dezember 2015 (englisch).

[24] Geiger, R. Aron, R.H., Todhunter, P. 2009: The Climate Near the Grond. 7. Ausgabe, Rowman & Littlefield, London. ISBN 978-0-7425-5560-0. (Rudolf Geiger: Das Klima der bodennahen Luftschicht. Verlag F. Vieweg & Sohn Braunschweig 1927 = Die Wissenschaft Bd. 78; 2. Aufl. ebd. 1942; ab 3. Aufl. Titel mit dem Zusatz Handbuch der Mikroklimatologie ebd. 1950; 4. Aufl. ebd. 1961. 5. Aufl. unter dem Titel The Climate near the Ground herausgegeben von Robert H. Aron und Paul Todhunter. Verlag F. Vieweg & Sohn Braunschweig 1995).

[25] Snell’s window in der englischen Wikipedia

[26] R. W. Wood: Fish-Eye Views, and Vision under Water. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Band 12, Nummer 6. In: Taylor & Francis Online. Johns Hopkins University, August 1906, S. 159-161, abgerufen am 3. Juni 2019 (englisch).

[27] Prof. R. W. Wood: Fischaugen-Sicht und das Sehen unter Wasser (Übersetzung). 1906, abgerufen am 25. August 2019.