Verzeichnung
Die Verzeichnung, oft fälschlicherweise auch (optische) Verzerrung genannt, ist ein geometrischer Abbildungsfehler optischer Systeme, der in der Linsengleichung zu einer lokalen Veränderung des Abbildungsmaßstabes führt. Die Maßstabsänderung beruht auf einer Änderung der Vergrößerung mit zunehmendem Abstand des Bildpunktes von der optischen Achse. Die Verzeichnung ist daher rotationssymmetrisch um einen Punkt, den Symmetriepunkt der Verzeichnung, der auch Verzeichnungszentrum genannt wird. Die Ursache der Verzeichnung liegt an Blenden bzw. begrenzenden Linsendurchmessern, die das Strahlenbündel der Abbildung vor oder hinter der Hauptebene eines optischen Systems mit Öffnungsfehler einengen[1]. Das heißt, dass Teile des zur Konstruktion des Strahlengangs zur Verfügung stehenden Strahlenbündels, ausgeblendet werden. Dadurch wird – gegenüber einem optischen System ohne Blende – die Richtung des Hauptstrahls geändert und verursacht die Verzeichnung.
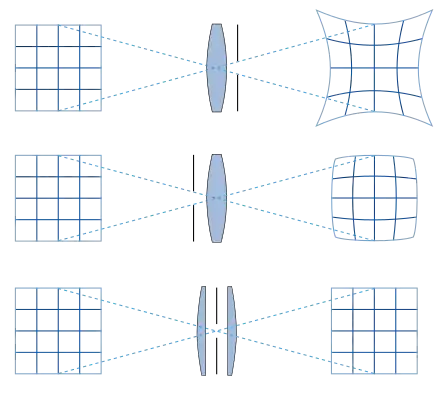
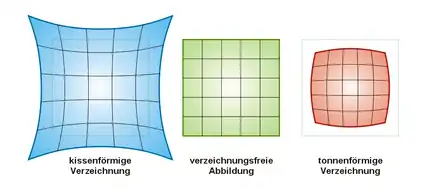
Nimmt die Vergrößerung zu den Rändern des Bildfelds zu, dann wird ein Quadrat kissenförmig verzeichnet. Im umgekehrten Fall spricht man von tonnenförmiger Verzeichnung. Es können auch Verzeichnungen höherer Ordnung auftreten, und die Überlagerung verschiedener Ordnungen kann zu einer wellenförmigen Abbildung gerader Linien führen („wellenförmige Verzeichnung“).


Bei optischen Geräten für den alltäglichen Gebrauch ist die Verzeichnung oft kein merklicher Nachteil und wird daher gegebenenfalls in Kauf genommen. So haben Brillen für Kurzsichtige zum Rand hin eine stark tonnenförmige Verzeichnung.
Bei Geräten mit mehreren Linsen, etwa bei Fernrohren, kann die Verzeichnung durch optische Korrektur gering gehalten werden:
- Verwendung von verschieden gekrümmten und unterschiedlich dicken Linsen
- Glassorten (Kronglas, Flintglas) mit unterschiedlichem Brechungsindex für die einzelnen Linsen.
Diese verzeichnungsfreien Optiken nennt man orthoskopische Linsensysteme. Bei visuell genutzten Optiken wird jedoch nicht selten eine kissenförmige Verzeichnung absichtlich implementiert, um den störenden Globuseffekt zu eliminieren.
Werden fotografische Abbildungen für präzise Messungen verwendet, können entsprechend korrigierte Linsensysteme eingesetzt werden, wie zum Beispiel telezentrische Objektive. Darüber hinaus kann die restliche Verzeichnung messtechnisch bestimmt und bei der Auswertung des Bildes rechnerisch kompensiert werden.
Die Verzeichnung eines Objektivs darf nicht mit der perspektivischen Verzerrung verwechselt werden. Die perspektivische Verzerrung kommt daher, dass eine Szene schräg betrachtet wird und dabei Seitenverhältnisse (Winkel) verloren gehen. So wird ein ebenes Quadrat, dass man aus einer beliebigen Zentralperspektive schräg betrachtet, zu einem allgemeinen Viereck verzerrt.
Kompensation
Speziell für die Bildmessung in der Photogrammetrie sind Methoden entwickelt worden, um die Verzeichnung eines Objektivs zu modellieren und zu berechnen (Kamerakalibrierung).
Durch Umkehrung dieser Modelle kann man die tatsächliche Verzeichnung eines Bildes kompensieren und ein verzeichnungsfreies Bild berechnen. Bei einer tonnenförmigen Verzeichnung wird das entzerrte Bild größer und bei einer kissenförmigen Verzeichnung kleiner, wenn der Abbildungsmaßstab in der Bildmitte unverändert bleibt. Manche Software erhält bei der tonnenförmigen Entzerrung das ursprüngliche Seitenverhältnis und schneidet brauchbare Bildinformation am Rand ab, obwohl ein größeres, unverzerrtes und rechteckiges Bild möglich wäre.
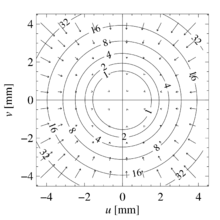
Das rechts stehende Bild zeigt die Verzeichnung eines Objektivs mit 20 Millimeter Brennweite bei Fokussierung bei einer Objektweite von einem Meter. Die Zahlen an den Isolinien geben den Betrag der Kompensation in Mikrometern an. Die Länge der Pfeile entspricht der fünfzehnfachen Länge der Änderung. Die Koordinaten und sind die Bildkoordinaten bezogen auf die Bildmitte.
Digitale Kamerasysteme, wie das Micro-Four-Thirds-System, können individuelle Eigenschaften von Objektiven, wie die Kenndaten der Verzeichnung an das Kameragehäuse übertragen, was eine automatische digitale Kompensation dieses geometrischen Abbildungsfehlers in der Kamera oder bei der nachfolgenden Bildbearbeitung ermöglicht.[2]
Mathematisches Verfahren
Im folgenden Text bezeichnet der Radius den Abstand eines Bildpunktes (auf dem Sensor) von der optischen Achse.
Bei einer perfekten Linse bleibt der Radius unverändert und es gilt: .
Eine gängige Beschreibung für die radialsymmetrische Verzeichnung ist das Polynom oder gleichwertig .
Bei Fischaugenobjektiven kann der Einfallswinkel größer als 180° sein und der Radius wäre unendlich groß: .
Daher wird hier der Winkel direkt als kubische Funktion dargestellt: .
Anwendungsbeispiele
In der Fotografie wird die Verzeichnung oft bewusst als künstlerisches Instrument eingesetzt. Insbesondere bei Fischaugenobjektiven ist der Effekt der Verzeichnung beabsichtigt.
Beim Fernsehen ist es oft nicht erwünscht, dass Zuschauer die reale räumliche Ausdehnung eines Studios erkennen können. Deshalb werden viele Studios – z. B. beim ZDF in Mainz – mit bogenförmigen Wänden oder gar kreisrund gebaut. Verwendet werden dann vorwiegend Weitwinkelobjektive. Deren Verzeichnung stört nicht – sie wird eher unbewusst wahrgenommen. Bei den Oberkanten der Wände – für Zuschauer die einzige „Marke“ für die Größe des Raumes – kann die Objektivverzeichnung dann nicht von der „echten“ Krümmung unterschieden werden; die Wand wirkt „endlos“.
Im Film und Videobereich werden anamorphe Verzeichnungen im Breitbildformat mit speziellen Kamera- und Objektivsystemen gezielt herbeigeführt. Ursprünglich wurden anamorphotisches Verfahren verwendet, um ohne Veränderungen am üblichen 35-Millimeter-Filmmaterial im Standard-Filmformat ein Breitbildformat im Kino zu ermöglichen. Dabei wurde das Breitbild bei der Filmaufnahme durch gezielte Verzerrung gequetscht – und bei der Wiedergabe im Kino durch entgegengesetzte Linsenanordnung wieder entzerrt. Damit wurde das Zeitalter des Breitwandkinos eingeführt – ohne den vollständigen Austausch der vorhandenen Kamera- und Projektionstechnik.
Doch nicht nur das Seitenverhältnis wurde mit anamorpher Technik beeinflusst: Es entstand ein filmischer Touch der bis dato als State-of-the-Art-Technik gilt. Viele filmische Effekte basieren auf anamorphen Linsen und erzeugen den „Cinelook“: Verringerte Schärfentiefe zur besseren Separation des Vorder- und Hintergrundes, oval geformte Lichteffekte (Bokeh), verzerrte Breitbild-Darstellung, ovale Lichtreflexe in Regenbogenfarben, streifenförmiges Blendlicht, Überstrahlung und beabsichtigte Verzerrung werden als künstlerische Werkzeuge verwendet.
Literatur
- DIN ISO 9039: Optik und Photonik – Qualitätsbewertung optischer Systeme – Bestimmung der Verzeichnung. (ISO 9039:2008)
- DIN 58187: Qualitätsbewertung optischer Systeme – Bestimmung der radialen Verzeichnung. (Juni 1986)
- Fritz Deumlich, Rudolf Staiger: Instrumentenkunde der Vermessungstechnik, 9. Aufl., Wichmann, Heidelberg, 2001, ISBN 3-87907-305-8.
- Karl Kraus: Photogrammetrie. de Gruyter, 2004, ISBN 3-11-017708-0.
- Harry Paul: Lexikon der Optik, Spektrum Akademischer Verlag, Heidelberg 2003, ISBN 3-8274-1422-9.
Weblinks
- B. Hönlinger und H. H. Nasse: Verzeichnung, zeiss.com vom Oktober 2009
Siehe auch
Einzelnachweise
- Verzeichnung, Wikibooks Digitale bildgebende Verfahren, Kapitel Bildaufnahme, abgerufen am 16. September 2015.
- Richard Butler: A distorted view? In-camera distortion correction, dpreview.com, 2. September 2011, abgerufen am 23. Januar 2016.