Totalreflexion

Die Totalreflexion ist eine bei Wellen auftretende physikalische Erscheinung. Für die Totalreflexion von elektromagnetischen Wellen ist das bekannteste Beispiel diejenige der Lichtwellen. Sie tritt bei flachem Auftreffen des Lichtes auf eine Grenzfläche zu einem anderen lichtdurchlässigen Medium mit geringerem Brechungsindex auf, in dem die Ausbreitungsgeschwindigkeit des Lichts größer als im Ausgangsmedium ist (z. B. in Luft größer als in Glas, siehe nebenstehende Abbildung). Bei allmählich flacher werdendem Auftreffen (größer werdendem sogenanntem Einfallswinkel) des Lichtes an der Grenzfläche tritt der Effekt relativ plötzlich auf. Der in diesem Moment wirksame Einfallswinkel wird als Grenzwinkel der Totalreflexion bezeichnet. Das Licht tritt nicht mehr größtenteils in das andere Medium über, sondern wird ab jetzt mehr oder weniger total ins Ausgangsmedium zurückgeworfen (reflektiert).

Totalreflexion von Licht an einer Grenzfläche zwischen Glas und Luft: Das flach auf die ebene Grenzfläche fallende Licht wird total reflektiert (an der runden Grenzfläche trifft es steil auf und kann aus dem Glas wieder austreten).

Die folgenden Darstellungen beziehen sich weiter vorwiegend auf das Beispiel der Lichtwellen, obwohl Totalreflexion bei allen Arten von Wellen auftritt.

Physikalische Erklärung

Huygenssches Prinzip

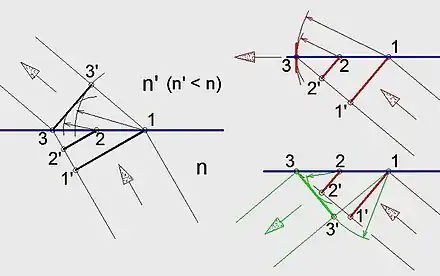
Huygenssches Prinzip: Brechung, und Reflexion einer Wellenfront
links: Brechung; rechts-oben: Übergangssituation; rechts -unten: Reflexion

In der Einleitung wurde ohne besonders darauf hinzuweisen das idealisierte Modell der Strahlenoptik angewendet. Dieses ist zur Erklärung der Refraktion und der damit zusammenhängenden Totalreflexion nicht geeignet. Geeignet ist die Anwendung der allgemeiner formulierten Wellenoptik und daraus die Anwendung des huygensschen Prinzips.

Demnach ist jeder Punkt, der von einer Wellenfront erreicht wird, Ausgangspunkt für eine kugel- bzw. kreisförmige Elementarwelle, welche sich im selben Medium mit gleicher Geschwindigkeit ausbreitet wie bzw. nach dem Übertritt in ein anderes Medium mit der dort anderen Geschwindigkeit ausbreitet als die ursprüngliche Welle. Die neue Lage der Wellenfront ergibt sich durch Überlagerung (Superposition) sämtlicher Elementarwellen. In nebenstehender Abbildung (linkes Teilbild) tritt eine Wellenfront von einem optisch dichteren Medium (unten) in ein optisch dünneres Medium (oben) über. Die Ausbreitungsgeschwindigkeit der Elementarwellen wird größer, weshalb die sich im dünneren Medium befindliche Front 3-3' der Welle eine andere Richtung hat als die vorherige 1-1', die sich noch im dichteren Medium befindet. 3-3' ist gegenüber 1-1' verdreht (der Winkel zwischen der Front und der Normale der Grenzfläche ist kleiner geworden).

Dies lässt sich bei Betrachtung von lediglich zwei von der Grenzschicht (Punkte 1 und 2) ausgehenden Elementarwellen bereits zeigen:

Wenn die Front 1-1' in die Lage 2-2' gekommen ist und die Distanz 1'-2' zurückgelegt hat, ist die von 2 ausgehende Welle schon weiter gekommen, als diese Distanz beträgt.
Wenn der Front-Punkt 1' im Punkt 3 angekommen ist und somit die Distanz 1'-3 zurückgelegt hat, ist die von 1 ausgehende Welle schon weiter gekommen, als diese Distanz beträgt.
Die gemeinsame Tangente dieser beiden Elementarwellen ist die neue Wellenfront 3-3'.

Wenn man die Wellenfront im dichteren optischen Medium (unten) immer schräger gegen die Grenzlinie laufen lässt, so ist die neue Wellenfront im optisch dichteren Medium soweit verdreht, dass sie auf der Grenzlinie fortläuft: Die beiden Elementarwellen haben eine gemeinsame Tangente im Punkt 3 (Abbildung, rechts-oben; zur Verbesserung der Anschauung stelle man sich die Breite der Welle so klein wie die Strichbreite der Grenzlinie in der Abbildung vor). Die Ausbreitungsrichtung der Lichtwelle hat jetzt den Grenzwinkel zur Totalreflexion erreicht. Die Welle tritt nicht mehr in das optisch dünnere Medium (oben) über, sondern wird bei weiter steigendem Einfallswinkel total in das optisch dichtere Medium (unten) zurück reflektiert (Abbildung, rechts-unten).

Snelliussches Brechungsgesetz

Totalreflexion
rot: Reflexion beim flachen Auftreffen von Licht, das aus einem optisch dichteren Medium kommend auf ein optisch dünneres trifft
gelb: Grenzsituation zwischen Brechung (grün) und Reflexion (rot)

Für die quantitative Behandlung der oben erklärten Zusammenhänge ist die Strahlenoptik gut geeignet. Im snelliusschen Brechungsgesetz wird sie angewendet.

Ein Lichtstrahl, der in einem optisch dichteren Medium (Brechungsindex $n_{1}$ ) sich ausbreitet und auf die Grenzfläche zu einem optisch dünneren Medium (Brechungsindex $n_{2}$ ) fällt, wird gemäß dem snelliusschen Brechungsgesetz vom Lot weg gebrochen – der Ausfallswinkel $\theta _{2}$ des Strahls ist größer als sein Einfallswinkel $\theta _{1}$ . Dieser Fall entspricht dem grünen Strahlenweg in der nebenstehenden Abbildung.

Vergrößert man den Einfallswinkel $\theta _{1}$ , so verläuft der gebrochene Strahl bei einem bestimmten Wert parallel zur Grenzfläche (gelber Strahlenweg). Dieser Einfallswinkel wird Grenzwinkel der Totalreflexion oder auch kritischer Winkel $\theta _{\mathrm {c} }$ genannt. Der Wert dieses Winkels lässt sich aus den beiden Brechungsindices berechnen:

\theta _{\mathrm {c} }=\arcsin \left({\frac {n_{2}}{n_{1}}}\right)

.

Das snelliussche Brechungsgesetz gilt nur, wenn der Lichtstrahl ins andere Medium übertritt, um dabei gebrochen zu werden. Für Einfallswinkel größer $\theta _{\mathrm {c} }$ würde man damit Ausfallswinkel größer 90° errechnen, was zu dieser Vorgabe im Widerspruch steht. Für $\theta >\theta _{\mathrm {c} }$ gilt das Reflexionsgesetz. Der Ausfallswinkel ist wie bei der „normalen, externen“ Reflexion gleich dem Einfallswinkel (roter Strahlenweg). Anstatt Brechung findet (Total-)Reflexion statt.

Besonderheiten

Abklingende Welle

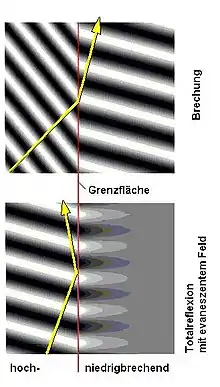
Evaneszente Felder hinter der Grenzfläche bei Totalreflexion. Gelb eingezeichnet sind die Ausbreitungsrichtungen der Wellen.

Die Mechanismen der Totalreflexion sind etwas anders als beispielsweise bei der Reflexion an metallischen Oberflächen. Aus den Maxwell-Gleichungen folgt, dass die elektromagnetische Welle an der Grenzfläche nicht schlagartig ihre Ausbreitungsrichtung ändern kann. Es bildet sich eine stehende Welle auf der Oberfläche aus, die ebenfalls in das nachfolgende optisch dünnere Material eindringt. Die Feldstärke dieser Welle im nachfolgenden Material nimmt dabei exponentiell ab. Die Eindringtiefe $d_{\mathrm {p} }$ (siehe auch London-Gleichung) bezeichnet dabei die Tiefe, bei der die Amplitude der abklingenden (evaneszente) Welle nur noch ca. 37 % (genauer: 1/ $e$ ) der Ausgangsamplitude besitzt.

Beschreibung der abklingenden Welle:

E(z)=E_{0}e^{-{\frac {z}{d_{\mathrm {p} }}}}

Eindringtiefe:

d_{\mathrm {p} }={\frac {\lambda }{2\pi n_{1}{\sqrt {\sin ^{2}\theta _{1}-\left({\frac {n_{2}}{n_{1}}}\right)^{2}}}}}

Eine weitere Besonderheit bei der Totalreflexion ist ein bei Experimenten beobachteter Strahlenversatz der sogenannten Goos-Hänchen-Verschiebung, d. h. der Ausgangspunkt der reflektierten Welle entspricht nicht dem Einfallspunkt der Welle.

Abgeschwächte und verhinderte Totalreflexion

Verhinderte Totalreflexion zwischen zwei nah aneinander liegenden Prismen

Die vorhergehende physikalische Beschreibung der Totalreflexion macht einige vereinfachende Annahmen. So wird die Reflexion an der Grenzfläche zweier unendlich ausgedehnter, dielektrischer Halbräume (transparente Materialien) betrachtet, was natürlich nicht den realen Vorgängen entspricht. Die gemachten Näherungen sind allerdings für die meisten Fälle ausreichend genau.

Einige Effekte sind mit diesen Vereinfachungen nicht erklärbar. Wird beispielsweise infrarotes Licht an der Grenzfläche von einem (infrarot transparenten) Prisma und Luft totalreflektiert, enthält das Spektrum der totalreflektierten Infrarotstrahlung Absorptionslinien von Kohlenstoffdioxid und Wasserdampf. Die Ursache dafür ist die abklingende Welle, die mit dem optisch dünneren Medium wechselwirkt, das heißt, bestimmte Strahlungsanteile werden durch das optisch dünnere Medium absorbiert. Diese frequenz- und materialabhängigen Absorptionsanteile (Absorptionszentren des zweiten, optisch dünneren Materials) sind im reflektierten Strahl sichtbar. Man spricht daher in diesem Fall von der abgeschwächten Totalreflexion (engl. attenuated total reflection, ATR). Dieser Effekt wird unter anderem bei der ATR-Infrarotspektroskopie ausgenutzt.

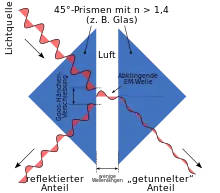
Ein anderer Effekt tritt ein, wenn hinter dem optisch dünneren Material ein optisch dichteres Material (Brechungsindex vergleichbar mit dem des ersten Materials) platziert wird. In Abhängigkeit vom Abstand zur Grenzfläche, an der die Totalreflexion stattfindet, werden Anteile der abklingenden Welle in das dritte Material transmittiert. Dabei kommt es wiederum zu einer Intensitätsabschwächung der eigentlich totalreflektierten Welle, weshalb man von der verhinderten oder frustrierten Totalreflexion (engl. frustrated total internal reflection, FTIR; nicht zu verwechseln mit Fourier-Transform-Infrarot-Spektrometern bzw. -spektroskopie) oder auch vom optischen Tunneleffekt spricht. Deutlich messbar wird dieser Effekt erst, wenn der Abstand zwischen erstem und drittem Material kleiner als etwa die doppelte Wellenlänge der einfallenden Welle ist.

Vorkommen in der Natur

Grüne Meeresschildkröte mit totalreflektierten Spiegelungen an der Wasseroberfläche

Das Funkeln geschliffener Diamanten, die „weiße“ Farbe von Zuckerkristallen oder faserigen Stoffen wie Papier sind – sofern sie nicht von Flüssigkeiten benetzt sind – wesentlich der Totalreflexion zuzuschreiben. Lichtstrahlen kommen in die Materialien hinein, aber erst nach einer mehr oder minder großen Zahl von Totalreflexionen wieder daraus heraus.

Das Wasser des Toplitzsees im Ausseerland hat ab einer Tiefe von etwa 20 m aufgrund natürlicher Solezuflüsse (siehe dort) einen erhöhten Salzgehalt[1]. An den Haloklinen beim Übergang vom optisch dichteren Medium (Salzwasser) zum optisch dünneren Medium (salzärmeres Oberflächenwasser) tritt in verschiedenen Wasserschichten weitgehend Totalreflexion auf, reflektierte oder gestreute Lichtstrahlen bleiben (wie bei einem Solar Pond) „gefangen“, daraus resultiert das bekannte „schwarze Wasser“ des Toplitzsees (der kein Moorsee ist).

Technische Anwendungen

Ultraviolette, sichtbare und infrarote Strahlung

Zweimalige Totalreflexion in einem Prisma

Im Bereich des sichtbaren Lichtes ist der Brechungsindex der meisten Materialien größer als von Vakuum (oder Luft). Dies wird zum Beispiel in Umlenkprismen und in Lichtwellenleitern ausgenutzt. Hier tritt die Totalreflexion beim Übergang vom optisch dichteren Medium (Prisma, Faserkern) zur optisch dünneren Umgebung (Luft) auf, in der Glasfaser ist die dünnere „Umgebung“ i. A. eine andere Glassorte. Licht kann derart nahezu verlustfrei in eine gewünschte Richtung gelenkt werden. Glasfaserkabel können Informationen in Form des Lichtes so bis zu 20.000 Meter weit transportieren, ohne dass eine Verstärkung notwendig wird.

Ein anderes Anwendungsfeld ist der Einsatz der Totalreflexion auf Doppelbrechung basierte Polarisatoren. Dabei wird die Eigenschaft ausgenutzt, dass doppelbrechende Materialien polarisationsabhängige Brechungsindizes aufweisen, so dass in einem bestimmten Einfallswinkelbereich eine Polarisation zum Großteil transmittiert und die andere totalreflektiert wird. Dieses Verhalten kann man auch für polarisationsabhängige Strahlteiler nutzen.

Eine andere Form von Strahlteiler kann unter Nutzung der verhinderten Totalreflexion realisiert werden. Hierbei werden zwei Prismen in sehr geringen Abstand (im Bereich einer Wellenlänge des Lichtes) zueinander platziert, dabei wird ein Teil der Welle reflektiert und der andere in das zweite Prisma transmittiert. Über den Abstand lässt sich zusätzlich das Verhältnis zwischen den beiden Anteilen einstellen. Anwendung findet dieses Prinzip beispielsweise in der Holografie oder als optische Weiche bei der Übertragung mittels Lichtwellenleiter.

Auch in der Messtechnik finden die erwähnten Effekte vielfältige Anwendung. So wird die abgeschwächte Totalreflexion seit Ende der 1960er Jahre im Bereich der Infrarotspektroskopie (genauer ATR-IR-Spektroskopie) eingesetzt. Durch die geringe Eindringtiefe lassen sich so auch dünne und stark absorbierende Materialien, wie wässrige Lösungen, untersuchen. Störende Interferenzen, wie sie bei der Transmissionsmessung von dünnen Schichten zu beobachten sind, treten dabei nicht auf. Ein ähnlicher Vorteil ergibt sich in der Fluoreszenzmikroskopie und dabei speziell bei der TIRF-Mikroskopie. Dort bewirkt die geringe Eindringtiefe, dass deutlich weniger Material zum Fluoreszieren angeregt wird, was einen höheren Kontrast zur Folge hat. Weiterhin wird das zumeist empfindliche organische Material weniger schnell zerstört.

Röntgenstrahlung

Der Brechungsindex $n$ aller Materialien ist bei Röntgenstrahlung leicht kleiner als 1 (Vakuum), dies im Unterschied zum sichtbaren Bereich, wo dieser fast immer deutlich größer als 1 ist. Da sich die Werte meist erst nach der siebten Nachkommastelle unterscheiden (also 0,999999(x)), wird in diesem Bereich häufig $\delta$ angegeben statt $n=1-\delta$ . Typische Werte für $\delta$ liegen im Bereich zwischen 10⁻⁹ und 10⁻⁵ und sind abhängig von der Quantenenergie der Strahlung, der Ordnungszahl und der Dichte des Materials.

Damit ist es möglich, im streifenden Einfall (θ gegen 90°) eine äußere Totalreflexion beim Übergang vom Vakuum zur Materie (also von „optisch“ dichteren zum „optisch“ dünneren Medium) zu erreichen. Ausgenutzt wird die Totalreflexion von Röntgenstrahlung in der Röntgenoptik; beispielsweise beruhen Kapillaroptiken auf diesem Prinzip.

Im Brechungsindex kann zusätzlich eine Absorption des Materials repräsentiert werden. In diesem Fall ist der Brechungsindex eine komplexe Zahl, deren Imaginärteil den Extinktionskoeffizienten $k$ repräsentiert. Damit ergeben sich die Darstellungsmöglichkeiten $N=n+\mathrm {i} k=1-\delta +\mathrm {i} k=1-\delta -\mathrm {i} \beta$ (d. h. $k=-\beta$ ). Die meisten Materialien sind für Röntgenstrahlung nahezu transparent, damit ist der Extinktionskoeffizient $k$ in der Regel kleiner als 10⁻⁶ (Es gibt aber auch hier zwischen den Materialien Unterschiede von mehreren Größenordnungen bis zu 10⁻¹⁴). (Der Sinn der komplexen Darstellung ist, dass die Amplitude $E$ einer Welle als $E=E_{0}e^{\mathrm {i} \left(N{\frac {\omega }{c_{0}}}-\omega t\right)}=E_{0}e^{\mathrm {i} \left((1-\delta +\mathrm {i} k){\frac {\omega }{c_{0}}}-\omega t\right)}$ formuliert werden kann.)

Siehe auch

Commons: Totalreflexion – Album mit Bildern, Videos und Audiodateien

Evanescent Wave Scattering

Einzelnachweise

Steirischer Seenbericht (2008), Steiermärkische Landesregierung, (PDF-Datei)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Steirischer Seenbericht (2008), Steiermärkische Landesregierung, (PDF-Datei)