Deskriptive Statistik
Die deskriptive (auch: beschreibende) Statistik hat zum Ziel, empirische Daten (z. B. Ergebnisse aus Experimenten) durch Tabellen, Kennzahlen (auch: Maßzahlen oder Parameter) und Grafiken übersichtlich darzustellen und zu ordnen. Dies ist vor allem bei umfangreichem Datenmaterial sinnvoll, da dieses nicht leicht überblickt werden kann.
Abgrenzung von anderen Teilgebieten der Statistik
Neben der deskriptiven Statistik gehören zur Statistik noch
- die explorative Datenanalyse (auch: erkundende Statistik) und
- die mathematische Statistik (auch: schließende Statistik, inferentielle Statistik oder induktive Statistik).
Die explorative Statistik hat zum Ziel, bisher unbekannte Strukturen und Zusammenhänge in den Daten zu finden und hierdurch neue Hypothesen zu generieren. Diese auf Stichprobendaten beruhenden Hypothesen können dann im Rahmen der schließenden Statistik mittels wahrscheinlichkeitstheoretischer Methoden auf ihre Allgemeingültigkeit untersucht werden.
Von der induktiven oder inferentiellen Statistik (Inferenzstatistik) unterscheidet sich die deskriptive Statistik dadurch, dass sie keine Aussagen zu einer über die untersuchten Fälle hinausgehenden Grundgesamtheit macht und keine Überprüfung von Hypothesen ermöglicht.[1] Die deskriptive Statistik verwendet keine stochastischen Modelle (Grundlage der induktiven Statistik), so dass die getroffenen Aussagen nicht durch Fehlerwahrscheinlichkeiten abgesichert sind.
Die Methoden der deskriptiven Statistik können daher bei jeder Art von Stichproben angewandt werden, während für die Methoden der induktiven Statistik eine Reihe von Voraussetzungen, unter anderem an die Stichprobenziehung, gestellt werden müssen. Die Methoden der explorativen Statistik sind meist identisch mit denen der deskriptiven Statistik; es ist eher das Ziel der Analyse, was beide Teilgebiete unterscheidet.
Methoden der deskriptiven Statistik
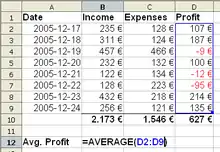Beispiel für eine Tabelle: Tabellenkalkulation mit OpenOffice.org
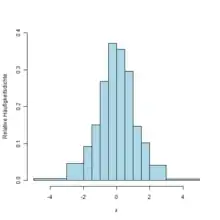Beispiel für ein Diagramm: Histogramm einer Variablen
Beispiel für einen Parameter: Koeffizienten für zwei Variablen
Um die Daten darzustellen gibt es im Wesentlichen drei Methoden:
- Tabellen
- In Tabellen werden Daten in einer Matrix mit Zeilen und Spalten dargestellt, wenn die Datenstruktur dies erlaubt. Dabei entspricht üblicherweise eine Zeile einer Beobachtung und eine Spalte einer Variablen der Daten. Der Nachteil einer Tabelle ist, dass bei selbst kleinen Datensätzen, die Struktur der Daten nur schwer zu erfassen ist. Manchmal kann das Umordnen von Spalten oder Zeilen helfen.
- Diagramme
- In Diagrammen und Grafiken werden die Daten bzw. bestimmte Aspekte derselben graphisch übersichtlich dargestellt. Dafür ist jedoch meist eine Zusammenfassung der Daten nötig, so dass Information aus den Daten verloren gehen. Zum Beispiel in einem Streudiagramm von zwei Variablen kann man gut die Relation zwischen den Daten erkennen, jedoch geht die Anzahl der Beobachtungen mit gleichen numerischen Werten verloren (overplotting).
- Parameter
- In Parametern (auch Maßzahlen oder Kennzahlen) wird ein Aspekt der Daten auf eine einzige Zahl reduziert (aggregiert). Um die Daten zu beschreiben, werden dann eine Vielzahl unterschiedlicher Parameter berechnet um den Informationsverlust durch die starke Zusammenfassung auszugleichen.
| Tabelle | Diagramm | Parameter | |
|---|---|---|---|
| Aggregation der Daten | niedrig | mittel | hoch |
| Übersichtlichkeit | niedrig | mittel | hoch |
| Informationsgehalt | hoch | mittel | niedrig |
Kenngrößen (statistische Kennwerte)
Drei Arten von Kenngrößen sind hauptsächlich von Interesse:
- Lagemaße
- als zentrale Tendenz einer Häufigkeitsverteilung. Aus der Lage der verschiedenen Werte für die zentrale Tendenz zueinander lassen sich Schiefe und Exzess einer Häufigkeitsverteilung bestimmen.
- Streuungsmaße
- für die Variabilität (Streuung oder Dispersion) einer Häufigkeitsverteilung und
- Zusammenhangsmaße
- für den Zusammenhang (auch: Korrelation) zweier Variablen.
Die Wahl der geeigneten Kenngrößen hängt vom Skalen- oder Messniveau der Daten und von der Robustheit der Kenngröße ab.
Beispiele
- Darstellung der Durchschnittstemperatur und der Temperaturschwankungen in einer Region durch Mittelwert und Streuung; Angabe, wie oft bestimmte Temperaturen überschritten werden (Quantil); Vergleich nach Regionen und/oder Zeiträumen mithilfe von Grafiken oder Tabellen.
- Vergleich der Abschlussnoten zweier Schuljahrgänge in einem Fach mit den jeweiligen Mittelwerten und Streuungen.
- In einer Urne sind fünf rote und vier blaue Kugeln. Es werden drei Kugeln ohne Zurücklegen aus dieser Urne gezogen. Definiert man die Zufallsvariable als die Anzahl der roten Kugeln unter den drei gezogenen, ist hypergeometrisch verteilt mit als Anzahl der roten Kugeln in der Urne, als Gesamtzahl der Kugeln in der Urne und als Anzahl der Versuche. Hier können alle Informationen über die Verteilung von gewonnen werden.
Siehe auch
Literatur
- Literatur über Deskriptive Statistik im Katalog der Deutschen Nationalbibliothek
- Hans Benninghaus: Deskriptive Statistik. Stuttgart 1976.
- Georg Bol: Deskriptive Statistik. Lehr- und Arbeitsbuch. 6. überarbeitete Auflage. Oldenbourg, München u. a. 2004, ISBN 3-486-57612-7.
- M. Burkschat, E. Cramer, U. Kamps: Beschreibende Statistik. Grundlegende Methoden. Springer, Berlin u. a. 2004, ISBN 3-540-03239-8 (EMILeA-stat).
- Ansgar Steland: Basiswissen Statistik. Kompaktkurs für Anwender aus Wirtschaft, Informatik und Technik. Springer, Berlin u. a. 2007, ISBN 978-3-540-74204-3 (Springer-Lehrbuch).
Weblinks
- Rößler, Irene / Ungerer, Albrecht: Formelsammlung zur deskriptiven Statistik (PDF; 2,1 MB)
- von der Lippe, Peter: Deskriptive Statistik: Formeln, Aufgaben, Klausurtraining (2006, 7,3 MB)
Einzelnachweise
- Jürgen Bortz: Statistik für Human- und Sozialwissenschaftler. 6. Auflage, Springer, Heidelberg 2005, ISBN 354021271X, S. 1.