Wölbung (Statistik)
Die Wölbung, Kyrtosis, Kurtosis oder auch Kurtose (griechisch κύρτωσις kýrtōsis „Krümmen“, „Wölben“) ist eine Maßzahl für die Steilheit bzw. „Spitzigkeit“ einer (eingipfligen) Wahrscheinlichkeitsfunktion, statistischen Dichtefunktion oder Häufigkeitsverteilung.[1] Die Wölbung ist das standardisierte (zentrale) Moment 4. Ordnung. Verteilungen mit geringer Wölbung streuen relativ gleichmäßig; bei Verteilungen mit hoher Wölbung resultiert die Streuung mehr aus extremen, aber seltenen Ereignissen.
Der Exzess gibt die Differenz der Wölbung der betrachteten Funktion zur Wölbung der Dichtefunktion einer normalverteilten Zufallsgröße an.[1]
Wölbung
Empirische Wölbung
Zur Berechnung der Wölbung einer empirischen Häufigkeitsverteilung wird die folgende Formel benutzt:
Damit die Wölbung unabhängig von der Maßeinheit der Variablen ist, werden die Beobachtungswerte mit Hilfe des arithmetischen Mittels und der Standardabweichung
standardisiert. Durch die Standardisierung gilt
Die Wölbung kann nur nicht-negative Werte annehmen. Ein Wert deutet darauf, dass die standardisierten Beobachtungen nahe dem Mittelwert konzentriert sind, d. h. die Verteilung ist flachgipflig (siehe Bild), für ist die Verteilung im Vergleich zu einer Normalverteilung spitzgipflig.
Wölbung einer Zufallsvariable
Analog zur empirischen Wölbung einer Häufigkeitsverteilung ist die Wölbung bzw. Kurtosis der Dichtefunktion bzw. Wahrscheinlichkeitsfunktion einer Zufallsvariablen definiert als ihr auf die vierte Potenz der Standardabweichung normiertes viertes zentrales Moment .
mit dem Erwartungswert .
Als Darstellung mittels der Kumulanten ergibt sich
Schätzung der Wölbung einer Grundgesamtheit
Zur Schätzung der unbekannten Wölbung einer Grundgesamtheit mittels Stichprobendaten ( der Stichprobenumfang) müssen der Erwartungswert und die Varianz aus der Stichprobe geschätzt werden, d. h. die theoretischen durch die empirischen Momente ersetzt werden:
mit dem Stichprobenmittel und der Stichprobenstandardabweichung .
Exzess
 |
 |
Um das Ausmaß der Wölbung besser einschätzen zu können, wird sie mit der Wölbung einer Normalverteilung verglichen, für die gilt. Der Exzess (auch: Überkurtosis) ist daher definiert als
Mittels der Kumulanten ergibt sich
Nicht selten wird die Wölbung fälschlicherweise als Exzess bezeichnet.
Arten von Exzess
Verteilungen werden entsprechend ihrem Exzess eingeteilt in:
- : normalgipflig oder mesokurtisch. Die Normalverteilung hat die Kurtosis und entsprechend den Exzess .
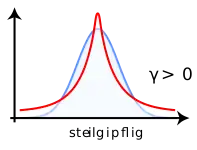
- : steilgipflig, supergaußförmig oder leptokurtisch. Es handelt sich hierbei um im Vergleich zur Normalverteilung spitzere Verteilungen, d. h. Verteilungen mit starken Peaks.
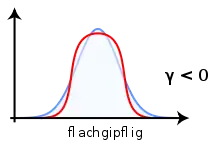
- : flachgipflig, subgaußförmig oder platykurtisch. Man spricht von einer im Vergleich zur Normalverteilung abgeflachten Verteilung.
Siehe auch
Einzelnachweise
- Bernd Rönz, Hans G. Strohe: Lexikon Statistik. Gabler Verlag, 1994, ISBN 3-409-19952-7, S. 115.