Häufigkeitsverteilung
Eine Häufigkeitsverteilung ist in der mathematischen Statistik zunächst eine Funktion, die zu jedem vorgekommenen wie auch zu jedem möglichen Wert angibt, wie häufig dieser Wert vorgekommen ist. Es wird also im Sinne des Begriffs der Funktion jedem Element der Definitionsmenge, die hier die Menge der möglichen Ausprägungen eines Merkmals umfasst, ein Element aus der Wertemenge zugeordnet, die hier aus den gezählten relativen oder absoluten Häufigkeiten besteht.
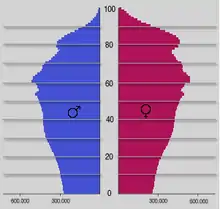
Gleichzeitig ist die Verwendung dieser Funktion und insbesondere ihre grafische Darstellung eine in hohem Maße geeignete Methode zur statistischen Beschreibung von Daten (Messwerten, Merkmalswerten) und ihrer anschaulichen Darstellung. Wie jede Funktion kann eine solche Verteilung als Tabelle, als Grafik oder modellhaft über eine Funktionsgleichung beschrieben werden.
Die Häufigkeitsverteilung ist in der Deskriptiven Statistik die Entsprechung zur Wahrscheinlichkeitsverteilung in der Wahrscheinlichkeitstheorie und der schließenden Statistik. Letztere bietet eine Reihe mathematischer Funktionen, die zur Annäherung und Analyse von Häufigkeitsverteilungen herangezogen werden (wie etwa die Normalverteilung).
Verfahren
Die Datenmenge (Messwerte, Umfragedaten) bildet die zunächst ungeordnete Urliste. Als erstes wird sie geordnet oder sortiert. Aus der geordneten Urliste (Rangliste) lassen sich bereits Medianwert, Spannweite (statistische Streuung), Quantile und Interquartilsabstand entnehmen und die Standardabweichung abschätzen.
Anschließend werden gleiche Werte zusammengefasst und zu jedem Wert notiert, wie oft dieser vorkommt. Dies wird als die absolute Häufigkeit bezeichnet. Werden die absoluten Häufigkeiten auf die Gesamtzahl der Werte einer sogenannten Stichprobe (Probenumfang) in Beziehung gesetzt, so können die relativen Häufigkeiten bestimmt werden. Nun liegt eine geordnete Menge von Wertepaaren (Merkmalswert und zugehörige relative Häufigkeit) vor. Dies kann auch als eine Rangfolge angesehen werden.
Die aufeinanderfolgende Summierung von relativen Häufigkeiten der einzelnen Merkmalswerte ergibt die Verteilungssumme respektive kumulierte Häufigkeit. Diese gibt für jeden Merkmalswert an, wie groß der Anteil an Werten kleiner oder gleich dem zugehörigen Merkmalswert ist. Bei vielen Häufigkeitsverteilungen beginnt diese bei dem Nullpunkt und verläuft bis zu einem Wert von eins beziehungsweise 100 Prozent. Werden die Werte grafisch dargestellt, ergibt sich eine schwach monoton steigende Kurve, meist in gestreckter S-Form. Es gibt zahlreiche Versuche, reale Verteilungssummen durch Funktionsgleichungen näherungsweise wiederzugeben. Die Verteilungssummen in Abhängigkeit von den Merkmalswerten sind die einfachste Art der Darstellung einer Häufigkeitsverteilung.
Die weitere Rechnung erfordert eine Einteilung der Merkmalswerte in Klassen. Dazu werden die vorkommenden Wertebereiche in meist gleich breite Klassen eingeteilt. Häufig werden dabei die seltenen Werte an den Rändern (siehe "Ausreißer") in größeren Klassen zusammengefasst. Dadurch ergeben sich die Dichtefunktionen, welche im Fall einer stetigen Verteilung die Ableitung der Empirischen Verteilungsfunktion nach dem Merkmalswert sind. Ferner lässt sich die Häufigkeit nicht nur durch Zählen ermitteln, sondern beispielsweise auch durch Wiegen. Dadurch ergibt sich eine Massenverteilung anstelle einer Anzahlverteilung. Im Prinzip eignet sich jede additive Größe zum Messen der Häufigkeit.
Wenn eine Zufalls-Stichprobe stark von der erwarteten Verteilung abweicht, kann dies durch den Stichprobenzufall, aber auch durch unerkannte Einflüsse, Auswahleffekte oder einen Trend verursacht sein. Besteht der Probenumfang in einer Überlagerung mehrerer Teilmengen (Altersverteilung, Berufe, Gruppen), so kann die Häufigkeitsverteilung statt eines Maximums auch zwei- oder mehrgipfelig sein.
Siehe auch
Literatur
- Lothar Sachs: Statistische Methoden. Springer, Berlin u. a. 1990, ISBN 3-540-52025-2.