Streudiagramm
Ein Streudiagramm, auch Punktwolke genannt (engl. scatter plot), ist die graphische Darstellung von beobachteten Wertepaaren zweier statistischer Merkmale. Diese Wertepaare werden in ein kartesisches Koordinatensystem eingetragen, wodurch sich eine Punktwolke ergibt. Die Darstellung der Punkte kann durch verschiedene Symbole erfolgen.
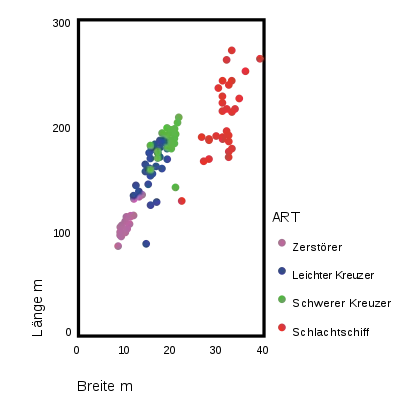
Anwendung
Man erhofft sich durch das Muster der Punkte im Streudiagramm Informationen über die Abhängigkeitsstruktur der beiden Merkmale zu erhalten, die durch die Koordinaten repräsentiert sind.
Nebenstehendes Beispieldiagramm enthält Punkte, die die beiden Merkmale „Länge“ und „Breite“ von verschiedenen Artillerieschiffen darstellen. Die Schiffe sind in vier Klassen eingeteilt, denen unterschiedliche Farben zugewiesen sind (Zerstörer, leichter Kreuzer, schwerer Kreuzer, Schlachtschiff). Man erkennt durch ein solches Streudiagramm auf einen Blick verschiedene Korrelationen in den erfassten Daten.
Häufig auftretende Korrelationen sind Cluster (Ballungen) und lineare Strukturen. Cluster können mit der Clusteranalyse untersucht werden. Zur Quantifizierung von linearen Korrelationen bietet sich vor allem die Regressionsanalyse an.
Falls ein drittes (metrisches) Merkmal auch noch mit dargestellt werden soll, kann das durch die Größe der Symbole geschehen. Den dabei entstehenden Diagrammtyp nennt man Blasendiagramm.
Bei diskreten Merkmalen
Im Allgemeinen sind nur stetig verteilte Daten für Streudiagramme geeignet. Beobachtungen diskret verteilter Merkmale überlagern sich, wenn gleiche Werte mehrfach vorliegen. Es gibt jedoch auch Möglichkeiten, ordinalskalierte Merkmale in Streudiagramme darzustellen:
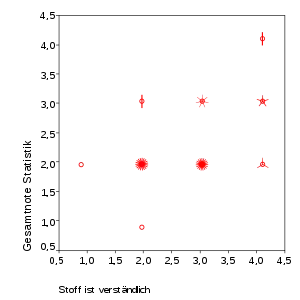
- durch „Sonnenblumen“: an jedem Koordinatenpaar wird ein Kreis eingetragen. Die Zahl der Wertepaare, die auf diesem Punkt liegen, wird durch Striche an den Kreis dargestellt, so dass sich eine stilisierte Sonnenblume ergibt.
- durch einen „Jittered Scatterplot“ („Verwackeltes Streudiagramm“): auf die Daten werden kleine Zufallszahlen addiert, so dass die Werte leicht auseinandergezogen werden und eine Punktwolke ergeben. Allerdings liegen die Werte eigentlich übereinander. Man könnte sie als „pseudometrisch“ bezeichnen.
Das folgende Beispiel zeigt beide Möglichkeiten anhand der Evaluation einer Statistik-Vorlesung, bei der die Merkmale „Stoff ist verständlich“ und „Gesamtnote Statistik“ (Noten von 1 bis 4) in ein Streudiagramm eingetragen wurden.
| Sonnenblumen-Streudiagramm | Jittered scatter plot |
|---|---|
 |
 |
Dot-Plot


Der Dot-Plot bzw. das Punktdiagramm wird auch als eindimensionales Streudiagramm bezeichnet. In ihm wird eine Variable entweder auf der x-Achse oder auf der y-Achse (wie in den Grafiken) dargestellt. Je nachdem, wie viele Werte die Beobachtungen der Variablen annehmen, ergibt sich das Problem, dass man nur einen Datenpunkt sieht, obwohl sich hinter ihm (viele) weitere Beobachtungen verbergen können.
Ähnlich wie beim Sonnenblumen-Streudiagramm können Symbole auf unterschiedliche Weisen genutzt werden, um die Anzahl der Punkte darzustellen. Dies soll an einem historischen Beispiel erläutert werden (Pferdetritt-Daten von Bortkewitsch):
- In der Grafik links symbolisiert ein größerer Kreis, dass sich hinter ihm mehr Beobachtungen verbergen als bei einem kleineren Kreis (Blasendiagramm).
- In der Grafik rechts wird für jeden Datenpunkt ein Kreis gezeichnet; tritt der gleiche Wert mehrfach auf, werden rechts neben dem ersten Kreis weitere Kreise gezeichnet.
Eine weitere Möglichkeit ist, auf der einen Achse den Beobachtungswert zu zeichnen und für die andere Achse einen zufälligen, z. B. aus einer Gleichverteilung stammenden, Wert zu wählen. Auch kann man eine Dichteschätzung einzeichnen.
Der Dotplot erlaubt Einblicke in die Verteilung einer Variablen, z. B. wo die Beobachtungen besonders dicht sind oder sich die Beobachtungen auf nur wenige Werte verteilen.
Streudiagramm-Matrix
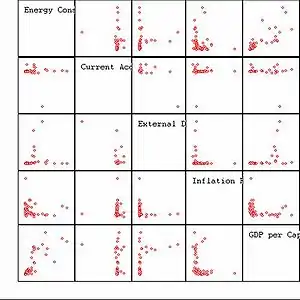
In der Streudiagramm-Matrix eines multivariaten Datensatzes werden für einzelne Paare von Variablen jeweils zwei Streudiagramme gezeichnet, die auf beiden Seiten (oben rechts / unten links) der mit Text gefüllten Matrix-Diagonalen liegen.
Dabei unterscheiden sich die beiden Streudiagramme, die zu einem Variablenpaar gehören, nur dadurch, welche Variable auf die x-Achse bzw. auf die y-Achse abgebildet wird. D. h. die entsprechenden Punktwolken auf beiden Seiten der Matrix-Diagonalen sind gespiegelt, aber nicht an der o. g. Diagonalen, sondern an ihren jeweiligen x=y-Linien, die alle senkrecht auf der Matrix-Diagonalen stehen.
In Variationen der Streudiagramm-Matrix werden statt der gespiegelten Punktwolken auch weitere Informationen dargestellt, z. B. Korrelationskoeffizienten oder Regressionsfunktionen.
Auf der Diagonalen sind in der Grafik rechts nur die Variablennamen eingetragen. Es gibt jedoch auch hier Variationen, z. B. mit weiteren Informationen (Box-Plots, Dichteschätzungen) über die jeweilige Variable.
Die Streudiagramm-Matrix hat einige Nachteile:
- Die Anzahl der dargestellten Variablen sollte nicht zu groß werden, da sonst die Fläche für jedes Streudiagramm zu klein und damit unübersichtlich wird. Die Streudiagramm-Matrix zeigt nämlich bei Variablen genau unterschiedliche Projektionen der multivariaten Daten (gespiegelte Darstellungen wie oben beschrieben nicht mitgezählt). Im dargestellten Beispiel ist und daher die Anzahl der unterschiedlichen Projektionen .
Die Brüder Tukey haben daher Maßzahlen vorgeschlagen, zusammenfassend mit Scagnostics bezeichnet, welche die Eigenschaft der Punktwolke charakterisieren. - Eine interessante Datenstruktur muss nicht in den Projektionen der Streudiagramm-Matrix sichtbar sein. Dann sollte man entweder auf die Grand Tour oder Projection-Pursuit-Verfahren zurückgreifen.