Histogramm

Ein Histogramm ist eine grafische Darstellung der Häufigkeitsverteilung kardinal skalierter Merkmale. Es erfordert die Einteilung der Daten in Klassen (englisch bins), die eine konstante oder variable Breite haben können. Es werden direkt nebeneinanderliegende Rechtecke von der Breite der jeweiligen Klasse gezeichnet, deren Flächeninhalte die (relativen oder absoluten) Klassenhäufigkeiten darstellen.[1][2][3] Die Höhe jedes Rechtecks stellt dann die (relative oder absolute) Häufigkeitsdichte dar, also die (relative oder absolute) Häufigkeit dividiert durch die Breite der entsprechenden Klasse.[4]

ein Histogramm

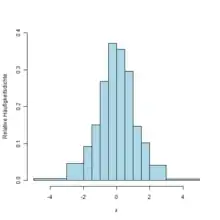
Anwendung

Anwendung finden Histogramme in der beschreibenden Statistik und in der Bildverarbeitung. Man verwendet Histogramme beispielsweise dann,

wenn man den Verlauf der Häufigkeitsverteilung sehen möchte und nicht nur zusammenfassende Daten wie das arithmetische Mittel und die Standardabweichung,
wenn man vermutet, dass mehrere Faktoren einen Prozess beeinflussen, und man diese nachweisen will
wenn man sinnvolle Spezifikationsgrenzen für einen Prozess definieren möchte.

In der physikalischen Forschung oder angewandten Gebieten (z. B. Analytik) werden gemessene Spektren als Histogramme dargestellt, siehe z. B. Vielkanalanalysator.

Konstruktion eines Histogramms

Folgende Schritte sind bei der Konstruktion eines Histogramms nötig:

Wertemenge in Klassen aufteilen (Breite der Rechtecke festlegen)
absolute/relative Klassenhäufigkeit bestimmen (Flächeninhalt der Rechtecke festlegen)
Häufigkeitsdichte bestimmen (Höhe der Rechtecke festlegen)
Histogramm grafisch darstellen

Einteilung in Klassen

Zur Konstruktion eines Histogramms wird der Wertebereich der Stichprobe in k aneinandergrenzende Intervalle geteilt, die Klassen.[5] Dabei ist darauf zu achten, dass die Randklassen nicht offen sind. Das heißt, die erste und die letzte Klasse müssen eine untere bzw. obere Grenze besitzen.[6][1] Die Klassen müssen nicht gleich breit sein. Allerdings vereinfachen zumindest im Mittelbereich gleich große Klassen die Interpretation. Über jede Klasse wird dann ein Rechteck errichtet, dessen Fläche proportional zur jeweiligen Klassenhäufigkeit ist. Im Histogramm entsprechen diese Klassen der Breite der einzelnen Rechtecke.

Bestimmung der Klassenhäufigkeit

Bei der Erstellung eines Histogramms gibt es zwei Vorgehensweisen: Die Klassenhäufigkeit spiegelt entweder einen absoluten oder einen relativen Wert wider. Der absolute Wert entspricht der Anzahl an Werten, die zu einer Klasse gehören. Der relative Wert hingegen drückt aus, wie viel Prozent der Werte einer Klasse angehören. Je nach Anwendungsfall kann sowohl das Arbeiten mit absoluten als auch mit relativen Werten Vorteile mit sich bringen. Im Histogramm entspricht die Klassenhäufigkeit dem Flächeninhalt der Rechtecke.

Bestimmung der Häufigkeitsdichte

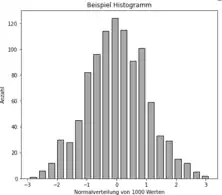
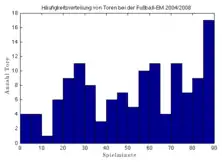
Beispiel für ein Histogramm mit einer Verteilung von 1000 Werten.

Beispiel für ein Histogramm mit konstanter Klassenbreite, bei dem die absoluten Häufigkeiten auf der Ordinate abgetragen sind.

Da die Fläche des j-ten Rechtecks gleich der Klassenhäufigkeit n_j ist, errechnet sich die Höhe des Rechtecks, die sogenannte Häufigkeitsdichte h_j, als Quotient n_j/d_j der Klassenhäufigkeit n_j durch die Klassenbreite d_j.[7] Dies wird unmittelbar klar, wenn man sich überlegt, dass die Fläche eines Rechtecks das Produkt aus Breite (Klassenbreite) und Höhe (Häufigkeitsdichte) ist. Die Klasse mit der größten Häufigkeitsdichte wird Modalklasse genannt.[8] Sind die Klassen gleich breit, so sind Häufigkeitsdichte und absolute bzw. relative Häufigkeiten proportional zueinander. Die Höhen der Rechtecke sind in diesem Fall vergleichbar und (unter Beachtung der Klassenbreite als Proportionalitätsfaktor) als Häufigkeit interpretierbar.

Statistische Schwankung der Klassenhäufigkeit

Oft werden die ermittelten Klassenhäufigkeiten beim Wiederholen der Datenerfassung streuen. So stellt sich, beispielsweise bei einer Wahlprognose, die Frage nach der Präzision der erhobenen Zahlen. Die zu erwartende Schwankungsbreite der Klassenhäufigkeit strebt bei unbegrenzt wachsender Anzahl der Klassen gegen ${\sqrt {n_{j}}}.$

Abschätzung der Anzahl der Klassen

Sturges-Regel

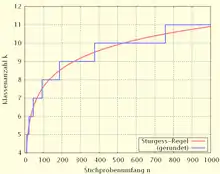
Um ein Histogramm zeichnen zu können, muss eine genügend große Anzahl an Messwerten einen sinnvollen Verlauf ergeben. Eine falsche Einteilung der Klassen kann zu einer Fehlinterpretation des Histogramms führen. Für die Festlegung der Anzahl der Klassen bzw. Rechtecke existieren verschiedene Faustregeln:

Anzahl der Messungen	Balkenzahl
<50	5 bis 7
50 bis 100	6 bis 10
100 bis 250	7 bis 12
>250	10 bis 20

Gegebenenfalls kann man die Anzahl der Balken $k$ auch nach der Sturges-Regel[9] berechnen:

k=1+\log _{2}n\approx 1+3{,}3\cdot \log _{10}n

Die Sturges-Regel hat den Nachteil, dass sie zum einen die Streuung nicht berücksichtigt. Zum anderen wählt sie die Klassenzahl zu klein für $n>200$ selbst im Fall einer (idealen) normalverteilten wahren Dichte.[10]

Alternativ kann die Klassenbreite $h$ mit der Regel nach Scott[11]

h={\frac {3{,}49\cdot \sigma }{\sqrt[{3}]{n}}}

oder der Regel nach Freedman und Diaconis[12]

h={\frac {2\cdot (Q_{3}-Q_{1})}{\sqrt[{3}]{n}}}

berechnet werden. Dabei sind $\sigma$ die Standardabweichung, $n$ die Anzahl der Messungen und $Q_{3}-Q_{1}$ der Interquartilsabstand.

Die Regel nach Scott ist so nur für normalverteilte Daten definiert. Für andere Fälle führte Scott Korrekturfaktoren in Abhängigkeit von Schiefe und Exzess ein.

Eigenschaften

Ein Histogramm ist eine flächenproportionale Darstellung der vorliegenden Häufigkeiten. Die Fläche eines Rechtecks entspricht $c\cdot f(x_{j})$ , wobei $f(x_{j})\,$ die relative Klassenhäufigkeit der Klasse $j\,$ und $c\,$ ein Proportionalitätsfaktor ist.

Ist $c\,$ gleich dem Stichprobenumfang, das heißt $c=n\,$ , so ist die Fläche eines jeden Rechtecks gleich der absoluten Klassenhäufigkeit. Das Histogramm wird in diesem Fall, in dem die Summe der Flächeninhalte der Rechtecke dem Stichprobenumfang n entspricht, absolut genannt.[13] Werden zur Konstruktion des Histogramms exakt die relativen Klassenhäufigkeiten verwendet ( $c=1\,$ ), wird das Histogramm als relativ oder normiert bezeichnet. Da die Flächeninhalte der Rechtecke nun den relativen Klassenhäufigkeiten entsprechen, summieren sich die Flächeninhalte in diesem Fall zu 1.[13]

Bei einem Histogramm grenzen die Rechtecke im Gegensatz zum Säulendiagramm direkt aneinander, das heißt, es existieren keine Abstände zwischen ihnen. Denn die Breite der Rechtecke entspricht den gebildeten Intervallen (Klassen), die ebenfalls direkt aneinandergrenzen.

Im Unterschied zum Säulendiagramm muss bei einem Histogramm die x-Achse immer eine Skala sein, deren Werte geordnet und gleichabständig sind.

Drei Kennzeichen eines Histogramms können zur Beurteilung der dargestellten Verteilung dienen:

der allgemeine Kurvenverlauf
die Streuung
die Zentrierung (Lageparameter (deskriptive Statistik))

Beispiel für ein Histogramm

Es liegen für 32 europäische Länder als Indikator für den Wohlstand die Zahlen der PKWs pro 1000 Einwohner vor. Die Werte werden wie folgt in Klassen eingeteilt:

Klasse j	Zahl der PKW pro 1000	Anzahl der Länder (absolute Klassenhäufigkeit) n_j	Klassenbreite d_j	Rechteckhöhe (Häufigkeitsdichte) h_j = n_j/d_j
1	über 0 – bis 200	5	200 – 0 = 200	0,025
2	über 200 bis 300	6	100	0,06
3	über 300 bis 400	6	100	0,06
4	über 400 bis 500	9	100	0,09
5	über 500 bis 700	6	200	0,03
Summe Σ		32

Mit Hilfe der Tabelle erhält man das folgende Histogramm:

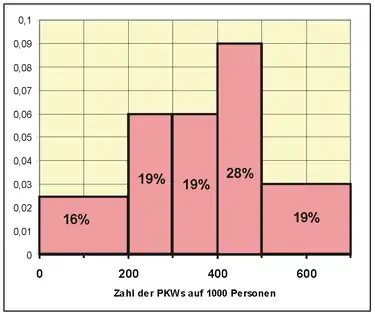
Histogramm der Zahl der PKWs auf 1000 Personen in 32 ausgewählten Ländern

Auf der Abszisse werden die Klassengrenzen und Klassenmittel abgetragen. In der Regel gibt man bei einem Histogramm die Ordinate nicht an, weil sonst die Gefahr besteht, die Höhe eines Rechtecks anstatt seiner Fläche als Häufigkeit zu interpretieren. Sind dagegen alle Klassen gleich breit, kann man für die Höhe der Rechtecke die Klassenhäufigkeit n_j verwenden und diese auf der Ordinate abtragen.

Average-Shifted-Histogramm

Das linke Bild zeigt vier Histogramme für den gleichen Datensatz. Zwar sind die Klassenbreiten in jedem Histogramm gleich 2,0, jedoch verschiebt sich der Beginn der ersten Klasse (-6.0, -5.5, -5.0 und -4.5). Obwohl jeweils der gleiche Datensatz benutzt wurde, kommen doch unterschiedliche Histogramme heraus.

Neben dem Problem der Klassenanzahl bzw. Klassenbreite spielt also auch die Wahl der (linken) Klassengrenzen eine Rolle. David Scott hat daher das Average-Shifted-Histogramm vorgeschlagen.[14]

Im rechten Bild wurden die vier Histogramme überlagert und dann für jeden Wert $x$ die Histogrammhöhen gemittelt. Dies ergibt das Average-Shifted-Histogramm. Üblicherweise werden deutlich mehr als vier Histogramme überlagert und gemittelt.

Das Average-Shifted-Histogramm löst das Problem der Wahl der (linken) Klassengrenzen, jedoch nicht das Problem der Wahl der optimalen Klassenbreiten.

Einzuordnen ist das Average-Shifted-Histogramm zwischen dem Histogramm und der Kerndichteschätzung.

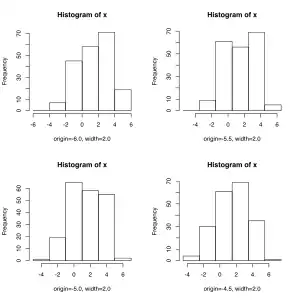Vier Histogramme für den gleichen Datensatz. Die Klassenbreiten sind in jedem Histogramm gleich 2,0. Lediglich der Beginn der ersten Klasse verschiebt sich von -6,0 über -5,5 und -5,0 auf -4,5.
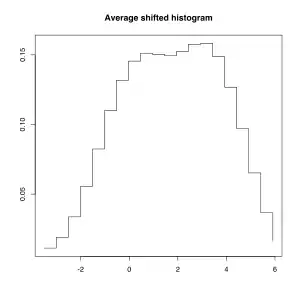Average-Shifted-Histogramm, berechnet aus den Überlagerungen der vier Einzelhistogramme.

Histogramm in der Bildverarbeitung

Histogramm eines Graustufen-Bildes mit einem hohen Anteil an Schwarz und Weiß

In der digitalen Bildverarbeitung versteht man unter einem Histogramm die statistische Häufigkeit der Grauwerte bzw. der Farbwerte in einem Bild. Das Histogramm eines Bildes erlaubt eine Aussage über die vorkommenden Grau- bzw. Farbwerte und über Kontrastumfang und Helligkeit des Bildes. In einem farbigen Bild kann entweder ein Histogramm über alle möglichen Farben oder Histogramme über die einzelnen Farbkanäle erstellt werden. Letzteres ist meist sinnvoller, da die meisten Verfahren auf Grauwertbildern basieren und so die sofortige Weiterverarbeitung möglich ist. Die Anzahl der Farbkanäle in einem Bild ist abhängig vom Modus, das heißt pro Farbauszug gibt es einen Kanal. Daher haben CMYK-Bilder vier Farbkanäle, RGB-Farbbilder nur drei.

Ein Histogramm visualisiert die Verteilung der Helligkeitswerte eines Bildes. Über einer Achse, die den Wertebereich der Farbwerte darstellt, sind als Balken die einzelnen Häufigkeiten des Vorkommens der Farbwerte aufgetragen. Je höher der Balken über einem Farbwert ist, desto häufiger kommt dieser Farbwert im Bild vor.[15]

Histogramme findet man häufig im Bereich der digitalen Fotografie. Gut ausgestattete digitale Fotoapparate zeigen auf dem Display während der Motivsuche als Hilfe für ein ausgewogeneres Bild in Echtzeit oder für bereits gespeicherte Aufnahmen ein Histogramm an. Das Betrachten eines Histogramms erlaubt es dem Fotografen, das Ergebnis oder das geplante Foto genauer zu kontrollieren, als es das Kameradisplay erlaubt. Zum Beispiel kann man typische Fehler wie Unter- und Überbelichtung erkennen und diese durch entsprechende Belichtungskorrektur beheben. Da die Helligkeit und vor allem der Kontrastumfang des Bildes bei der späteren Bearbeitung und Verwertung eine große Rolle spielen, lohnt es sich beim Fotografieren, auf die Histogrammanzeige zu achten.

Eine klassische Anwendung von Histogrammen in der Bildverarbeitung liegt in der Egalisierung (Äqualisierung, englisch equalizing), bei der das Histogramm mit einer Egalisierungsfunktion transformiert wird. Dadurch kann eine bessere Verteilung der Farbgebung erreicht werden, die über eine bloße Kontrastverstärkung hinausgeht.

Beispiel High-key- und Low-key-Fotografie

Histogramm einer High-key-Aufnahme: 70 % der Pixel in diesem Bild konzentrieren sich in den oberen 2 % (250 bis 255) des gesamten Tonwertumfangs (0 bis 255). Der Rest der Pixel (30 %) verteilt sich auf die restlichen 250 Tonwerte.

Bei Low-key-Aufnahmen konzentrieren sich die Details in den niedrigen Tonwerten. Der Ausschlag ist demnach im unteren Bereich am stärksten. (Es liegen viele Pixel mit niedrigen Tonwerten vor.)

Für High-key-Aufnahmen gilt das Gegenteil, also viele Pixel mit hohen Tonwerten und kaum ein Ausschlag in den niedrigen Tonwerten.

Bei überbelichteten Aufnahmen „schmiegt“ sich die Wahrscheinlichkeitskurve an der rechten (hellen) Seite an und das Maximum wird möglicherweise gar nicht erreicht. Es werden also nicht alle hellen Details wiedergegeben, da ein bestimmter Helligkeitsbereich abgeschnitten ist und der darunterliegende als weiß definiert wird.

Geschichte

Wohl erstmals tauchte ein Histogramm 1786 in der Arbeit The Commercial and Political Atlas des um 1800 lebenden schottischen Ingenieurs und Volkswirts William Playfair auf, der zuvor auch das Balken- und Tortendiagramm einführte.[16] Im Jahr 1833 verwendete auch der Franzose André-Michel Guerry Histogramme zur Visualisierung von Daten.[17] Weiterentwickelt wurde das Histogramm durch den belgischen Statistiker und Sozialwissenschaftler Adolphe Quetelet um 1846. Der Begriff „histogram“ (historical diagram)[18] wurde jedoch erstmals vom englischen Mathematiker Karl Pearson im Jahr 1891 in einer Vorlesungsreihe genutzt und schließlich 1895 in seiner heutigen Bedeutung eingeführt.[19][20][21]

Siehe auch

Weblinks

Commons: Histogramme – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Histogramm – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Weitere Informationen zum Histogramm bei Digitalkameras

Einzelnachweise

Bernd Rönz, Hans G. Strohe: Lexikon Statistik. Gabler Verlag, 1994, S. 157
Larry Wasserman: All of Nonparametric Statistics. Springer, 2005, S. 127
Arens et al.: Mathematik. Spektrum Akademischer Verlag, 2008, S. 1226
D. Freedman, R. Pisani, R. Purves: Statistics. Third edition. W.W.Norton, 1998.
Thomas A. Runkler: Data Mining: Methoden und Algorithmen intelligenter Datenanalyse. 1. Auflage. Vieweg + Teubner, 2010, S. 47.
Erhard Cramer, Udo Kamps: Grundlagen der Wahrscheinlichkeitsrechnung und Statistik: Ein Skript für Studierende der Informatik, der Ingenieur- und Wirtschaftswissenschaften. 2. Auflage. Springer, 2008, S. 45.
Wolfgang Brauch, Hans-Joachim Dreyer, Wolfhart Haacke: Mathematik für Ingenieure. Springer, 2013, ISBN 978-3-322-91830-7, S. 658 (eingeschränkte Vorschau in der Google-Buchsuche).
Bernd Rönz, Hans G. Strohe (1994), Lexikon Statistik, Gabler Verlag, S. 250
Herbert A. Sturges: The choice of a class interval. In: Journal of the American Statistical Association. Nr. 21, 1926, S. 65–66.
R. J. Hyndman: The problem with Sturges’ rule for constructing histograms. In: Technical report. Melbourne University.
David W. Scott: On optimal and data-based histogram. In: Biometrika. Band 3, Nr. 66, 1979, S. 605–610, doi:10.1093/biomet/66.3.605.
David Freedman, Persi Diaconis: n the histogram as a density estimator: $L_{2}$ theory. In: Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete. Band 57, Nr. 4, 1981, S. 453–476, doi:10.1007/BF01025868.
Jürgen Bortz: Statistik für Human- und Sozialwissenschaftler. 6. Auflage. Springer, 2005, S. 31–32.
David Scott: Multivariate Density Estimation: Theory, Practice, and Visualization. John Wiley, 1992, ISBN 978-0-471-54770-9.
Das bedeutet: Histogramm. test.de, 25. August 2011; abgerufen am 7. Januar 2013
Playfair, William; The Commercial and Political Atlas: Representing, by Means of Stained Copper-Plate Charts, the Progress of the Commerce, Revenues, Expenditure and Debts of England during the Whole of the Eighteenth Century, London 1786
André-Michel Guerry: Essai sur la Statistique Morale de la France. Paris 1833.
“He explained that the histogram could be used for historical purposes to create blocks of time of ‘charts about reigns or sovereigns or periods of different prime ministers’.” zitiert aus The Rutherford Journal
Sheldon M. Ross: Introductory Statistics. 2. Auflage. Elsevier Academic Press, 2005, S. 56–57.
Yadolah Dodge: The Concise Encyclopedia of Statistics. Springer, 2008, S. 236–237.
Eileen Magnello: Karl Pearson’s Gresham Lectures: W. F. R. Weldon, Speciation and the Origins of Pearsonian Statistics. In: The British Journal for the History of Science. Band 29, Nr. 1. Cambridge University Press, 1996, S. 48.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Roenz_S157-1] Bernd Rönz, Hans G. Strohe: Lexikon Statistik. Gabler Verlag, 1994, S. 157

[Wasserman2005-2] Larry Wasserman: All of Nonparametric Statistics. Springer, 2005, S. 127

[Arens2008-3] Arens et al.: Mathematik. Spektrum Akademischer Verlag, 2008, S. 1226

[4] D. Freedman, R. Pisani, R. Purves: Statistics. Third edition. W.W.Norton, 1998.

[5] Thomas A. Runkler: Data Mining: Methoden und Algorithmen intelligenter Datenanalyse. 1. Auflage. Vieweg + Teubner, 2010, S. 47.

[6] Erhard Cramer, Udo Kamps: Grundlagen der Wahrscheinlichkeitsrechnung und Statistik: Ein Skript für Studierende der Informatik, der Ingenieur- und Wirtschaftswissenschaften. 2. Auflage. Springer, 2008, S. 45.

[7] Wolfgang Brauch, Hans-Joachim Dreyer, Wolfhart Haacke: Mathematik für Ingenieure. Springer, 2013, ISBN 978-3-322-91830-7, S. 658 (eingeschränkte Vorschau in der Google-Buchsuche).

[Roenz_S250-8] Bernd Rönz, Hans G. Strohe (1994), Lexikon Statistik, Gabler Verlag, S. 250

[9] Herbert A. Sturges: The choice of a class interval. In: Journal of the American Statistical Association. Nr. 21, 1926, S. 65–66.

[10] R. J. Hyndman: The problem with Sturges’ rule for constructing histograms. In: Technical report. Melbourne University.

[11] David W. Scott: On optimal and data-based histogram. In: Biometrika. Band 3, Nr. 66, 1979, S. 605–610, doi:10.1093/biomet/66.3.605.

[12] David Freedman, Persi Diaconis: n the histogram as a density estimator: $L_{2}$ theory. In: Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete. Band 57, Nr. 4, 1981, S. 453–476, doi:10.1007/BF01025868.

[Bortz2005-13] Jürgen Bortz: Statistik für Human- und Sozialwissenschaftler. 6. Auflage. Springer, 2005, S. 31–32.

[14] David Scott: Multivariate Density Estimation: Theory, Practice, and Visualization. John Wiley, 1992, ISBN 978-0-471-54770-9.

[15] Das bedeutet: Histogramm. test.de, 25. August 2011; abgerufen am 7. Januar 2013

[16] Playfair, William; The Commercial and Political Atlas: Representing, by Means of Stained Copper-Plate Charts, the Progress of the Commerce, Revenues, Expenditure and Debts of England during the Whole of the Eighteenth Century, London 1786

[17] André-Michel Guerry: Essai sur la Statistique Morale de la France. Paris 1833.

[18] “He explained that the histogram could be used for historical purposes to create blocks of time of ‘charts about reigns or sovereigns or periods of different prime ministers’.” zitiert aus The Rutherford Journal

[19] Sheldon M. Ross: Introductory Statistics. 2. Auflage. Elsevier Academic Press, 2005, S. 56–57.

[20] Yadolah Dodge: The Concise Encyclopedia of Statistics. Springer, 2008, S. 236–237.

[21] Eileen Magnello: Karl Pearson’s Gresham Lectures: W. F. R. Weldon, Speciation and the Origins of Pearsonian Statistics. In: The British Journal for the History of Science. Band 29, Nr. 1. Cambridge University Press, 1996, S. 48.