Darstellende Geometrie
Darstellende Geometrie ist der Teilbereich der Geometrie, der sich mit den geometrisch-konstruktiven Verfahren von Projektionen dreidimensionaler Objekte auf eine zweidimensionale Darstellungsebene befasst. Die Anwendungsbereiche ihrer Methoden sind breit gefächert und erstrecken sich neben den heute bekanntesten Anwendungen in der Technik- und Architekturdarstellung auch auf Kunst, Malerei, Kartenwesen und Computergraphik. Die Darstellende Geometrie beschränkt sich nicht nur auf das Darstellen von räumlichen Objekten, sondern bietet auch Möglichkeiten raumgeometrische Probleme zeichnerisch zu lösen: z. B. die Bestimmung des Schnittpunktes einer Gerade mit einer Ebene oder die Schnittkurve zweier Flächen oder den Schatten eines Objektes.
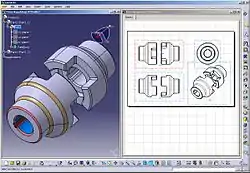Bildschirmfoto aus CATIA V5: Maschinenteil
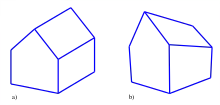
b) Zentralprojektion eines Hauses
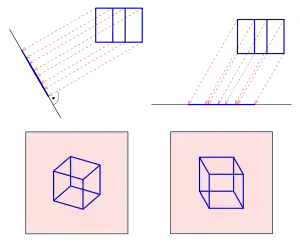
a) orthogonal
b) schief
Im Gegensatz zu früher (s. Weblink Gangolf Delabar) ist die Darstellende Geometrie nicht mehr das einzige Mittel, um räumliche Objekte anschaulich darzustellen oder raumgeometrische Probleme zu lösen. Hierfür verwendet man heute Computer (s. Weblinks und Geometrische Modellierung). Die Bedeutung der Darstellenden Geometrie liegt heute vielmehr im Training der Benutzer geometrischer Software, damit sie verstehen, was eine Software kann und an Eingaben verlangt. Für erste Skizzen einer (räumlichen) Idee oder Interpretationen und Ergänzungen von Computerzeichnungen ist das Zeichnen mit Zirkel und Lineal eine hervorragende Übung.
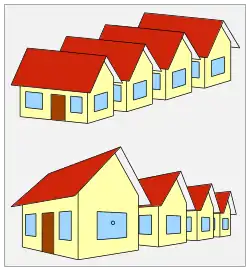
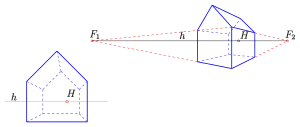
Bei der Darstellung räumlicher Objekte in einer Zeichenebene spielen zwei konkurrierende Gesichtspunkte eine wesentliche Rolle. Will man Maßgenauigkeit erreichen, so ist dies meistens nur unter Verlust von Anschaulichkeit möglich. Z. B. lassen die beiden folgenden Bilder eines Hauses leicht auf Länge, Breite und Höhe schließen; sie sind aber nicht sehr anschaulich. Dagegen bringen die nächsten beiden Bilder den räumlichen Eindruck mehr zur Geltung. Genaue Abmessungen lassen sich aber (insbesondere aus dem rechten Bild) nur schwer ablesen.
Abbildungsverfahren
In der Darstellenden Geometrie bedient man sich im Wesentlichen zweier Abbildungsverfahren. Dabei werden Punkte und Kurven eines Objektes mit Hilfe von Strahlen (Geraden) auf eine Bildtafel (Ebene) projiziert:
Parallelprojektion
Die Abbildungsstrahlen sind parallel, wie z. B. beim Sonnenlicht. Dabei unterscheidet man noch die beiden Fälle:
- Die Strahlen stehen senkrecht auf der Bildtafel (senkrechte Parallelprojektion oder Orthogonalprojektion oder Normalprojektion).
- Die Strahlen stehen nicht senkrecht zur Bildtafel (schiefe oder schräge Parallelprojektion).
Parallelprojektionen werden gerne von Ingenieuren verwendet wegen ihrer Teilverhältnistreue (Teilverhältnisse auf Geraden bleiben invariant). Der Spezialfall Vogelperspektive ist eine schiefe Parallelprojektion, die insbesondere zur Veranschaulichung von Stadtplänen verwendet wird. Sie lässt sich relativ einfach von Hand herstellen. Parallelprojektionen lassen sich schnell als axonometrische Bilder oder bei umfangreicheren Objekten mit Hilfe des Einschneideverfahrens herstellen.
Für fast alle Konstruktionen in der Darstellenden Geometrie verwendet man Grund- und Aufriss eines Objektes. Das sind senkrechte Parallelprojektionen auf eine horizontale (Grundriss) bzw. senkrechte Ebene (Aufriss) (s. Zweitafelprojektion). Durch sie ist (mit den entsprechenden Bezeichnungen) ein Objekt räumlich eindeutig beschrieben.
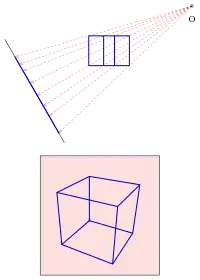
Zentralprojektion
Alle Abbildungsstrahlen gehen durch einen Punkt, dem Projektionszentrum oder Augpunkt . Bei Parallelprojektion sind die Bilder paralleler Geraden i. A. wieder parallel. Bei Zentralprojektionen schneiden sich die Bilder paralleler Geraden i. A. in einem Punkt, dem Fluchtpunkt des Parallelbüschels.
Dass eine Zentralprojektion den besten optischen Eindruck verschafft, zeigen die Bilder mit einer Häuserreihe. Bei dem Bild in Parallelprojektion erscheint das hintere Haus größer als das erste. Dies liegt an einer optischen Täuschung. Das Auge erkennt das Haus als räumliches Objekt und erwartet, dass ein gleich großes, entferntes Haus kleiner ist, was bei Parallelprojektion aber nicht der Fall ist.
Darstellung realer Objekte
Um Objekte wie Häuser, Brücken, ... in einer handlichen Zeichenebene oder auf einem Bildschirm darstellen zu können, werden die Abmessungen der Objekte üblicherweise vor einer Projektion geeignet skaliert (verkleinert), z. B. mit Faktoren 1/10, 1/50 oder 1/100.
Hilfsmittel
Technische Hilfsmittel
Klassische Hilfsmittel bei der Erstellung von Zeichnungen sind: Papier als ebene Zeichenfläche, Bleistift, Zirkel, Lineal, Geodreieck und Kurvenlineal als Zeichengeräte. Computer mit geeigneter Software (z. B. Cinderella, GeoGebra, Inkscape, Xfig, …) können heute all diese Hilfsmittel ersetzen. Manuell steuert man solch einen graphikfähigen Computer mit einer Computer-Maus. Will man das Ergebnis schwarz auf weiß auf Papier vor sich haben, verwendet man einen computergesteuerten Drucker. Allerdings werden die klassischen Hilfsmittel (ohne Computer) auch heute noch als Grundlage bei der Ausbildung von Architekten und Ingenieuren verwendet.
Theoretische Hilfsmittel
Als theoretische Hilfsmittel verwendet man grundlegende Aussagen aus der klassischen Geometrie: Strahlensätze, die Sätze von Pythagoras und Thales, Sätze über Dreiecke, Sätze über Kegelschnitte (Ellipsen, …), Eigenschaften von Quadriken (Kugel, Kegel, Zylinder, …).
Methoden der Darstellenden Geometrie
Projektionen: Zweitafelprojektion, Axonometrie, Architektenanordnung, Frontalperspektive
Die wichtigsten Arbeitsmittel in der Darstellenden Geometrie sind Grund- und Aufriss und deren Zuordnungen. Sie liefern die räumlichen Informationen für spezielle Darstellungen und Konstruktionen. Das Wissen darüber lernt man in
- Zweitafelprojektion: Gelegentlich ist es nötig, weitere Risse einzuführen. Man spricht dann auch von Umprojektionen und Mehrtafelprojektionen.
Mit Grund- und Aufriss lassen sich dann mit Hilfe von
- Axonometrie,
- Einschneideverfahren,
- Orthogonaler Axonometrie und
- Umrisskonstruktion (für gekrümmte Flächen; siehe hierzu auch Kanalflächen)
anschauliche Bilder von räumlichen Objekten in Parallelprojektion herstellen.
Bilder in Zentralprojektion konstruiert man am besten mit der
- Architektenanordnung (ähnlich dem Einschneideverfahren für Parallelprojektionen) und der
- Frontalperspektive (Perspektive mit einem wesentlichen Fluchtpunkt, dem Hauptpunkt).
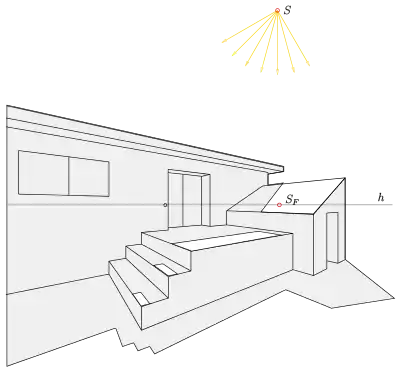
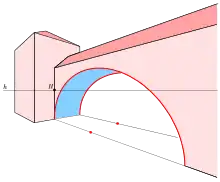
Um verzerrt wirkende Bildteile zu vermeiden, sollte man nach der Wahl der Lage von Bildtafel, Hauptpunkt und Augpunkt zunächst den
einzeichnen. Denn nur Bildteile innerhalb des Sehkreises erscheinen im perspektiven Bild unverzerrt.
Durchdringungen: Schnittpunkte und Schnittkurven
Eine wichtige Grundaufgabe der Darstellenden Geometrie ist die (zeichnerische) Bestimmung des Schnittpunktes einer Gerade und einer Ebene. Das Verfahren hierzu heißt
- Durchstoßpunkt-Verfahren.
- (Rechnerische Verfahren zur Bestimmung eines Schnittpunktes findet man hier.)
Durchstoßpunkte werden z. B. benötigt bei der
Zu den Grundaufgaben gehören auch die Bestimmung der
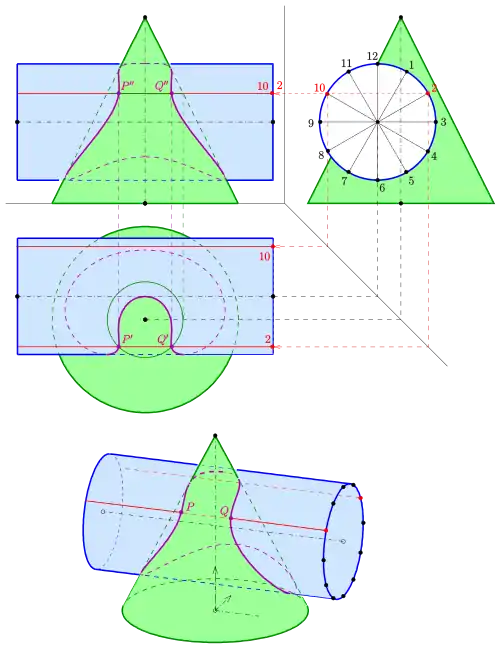
Für die Konstruktion von Punkten der Schnittkurve zweier Flächen (Zylinder, Kegel, Kugel, Torus, Rotationsfläche) gibt es vier Standardverfahren:
- das Hilfsebenenverfahren,
- das Mantellinienverfahren,
- das Pendelebenenverfahren und
- das Hilfskugelverfahren.
- (Rechnerische Verfahren zur Bestimmung einer Schnittkurve findet man hier.)
Bei der Herstellung von Modellen sich durchdringender Zylinder und/oder Kegel werden oft aufgewickelte Abwicklungen dieser Flächen verwendet. Wie man Zylinder und Kegel abwickelt, wird in
beschrieben.
Eintafelprojektionen: kotierte Projektion, Dachausmittlung
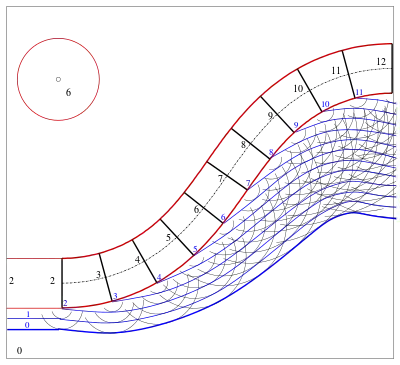
Neben den Zwei- und Mehrtafelprojektionen gibt es noch spezielle Eintafelprojektionen. Dabei handelt es sich um Grundrisse mit Zusatzinformationen, die die Objekte räumlich beschreiben. Im Straßenbau verwendet man die
- Kotierte Projektion, um
- Böschungsflächen zu konstruieren und darzustellen.
Mit der Konstruktion von Grat-, Kehl- und Firstlinien (Schnittgeraden) von ebenen Dachflächen befasst sich die
Wahre Länge, wahre Gestalt und Rekonstruktion
Geneigte Strecken oder ebene Figuren in Parallelprojektionen entzerrt man mit
Analoge Methoden für Zentralprojektionen (Fotos) bietet die
Kreis und Kugel
Kreise und Ellipsen spielen insbesondere als Berandungskurven von Objekten wie Zylindern, Kegeln und Rotationsflächen eine wichtige Rolle (s. Bilder: Turm mit Tor, Brücke in Frontalperspektive). Wie man sie mit Parallelprojektion und Zentralprojektion abbildet und anschließend zeichnet, wird in
beschrieben. Wichtige Hilfsmittel dabei sind
- Konjugierte Durchmesser einer Ellipse und die
- Rytzsche Achsenkonstruktion, mit der man die Hauptachsen einer Ellipse rekonstruiert, um die Ellipse schließlich mit der
- Scheitelkrümmungskreismethode zu zeichnen.
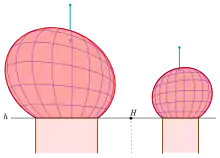
Die Darstellung einer Kugel ist bei senkrechter Parallelprojektion sehr einfach. Ihr Umriss ist ein Kreis mit dem Radius der Kugel. Bei allen anderen wesentlichen Projektionsarten, wie Vogelperspektive, Kavalierperspektive und Zentralprojektion, erscheint der Umriss einer Kugel, von Sonderfällen abgesehen, als Ellipse. Wie man die Umrissellipse einer Kugel konstruiert, wird in
erklärt.
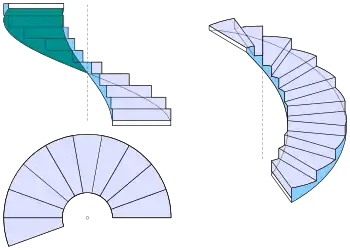
Schraublinien
Schraublinien spielen in der Architektur bei der Darstellung von Wendeltreppen und in der Technik von Schrauben und Spiralbohrer eine wesentliche Rolle. Ihre Darstellung in Grund- und Aufriss, sowie orthogonalen und schiefen Parallelprojektionen wird in
beschrieben.
Spiegelungen
Wie man in vorhandenen Bildern (Axonometrien oder Zentralprojektionen) Spiegelbilder von Objekten, die durch Reflexion an Wasseroberflächen oder Wandspiegeln entstehen, einzeichnet, wird in
erklärt.
Spezielle Perspektiven (Ansichten)
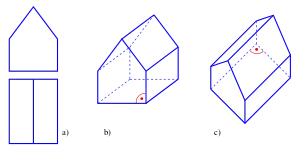
a) Grund- und Aufriss
b) Kavalierperspektive
c) Vogelperspektive
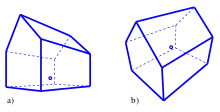
a) Froschperspektive
b) Vogelperspektive
Die Grundlage für fast alle Darstellungen und Konstruktionen in der Darstellenden Geometrie sind
- Grund- und Aufriss: Senkrechte Parallelprojektionen auf eine horizontale bzw. senkrechte Bildtafel.
Das Wort Perspektive wird in der Darstellenden Geometrie vielfach benutzt, um besondere anschauliche Ansichten eines räumlichen Objektes zu benennen:
- Die Kavalierperspektive oder Kabinettperspektive ist eine schiefe Parallelprojektion (s. Axonometrie) auf eine senkrechte Bildtafel. Alle ebenen Figuren, die parallel zur Bildtafel sind, werden unverzerrt abgebildet (s. Bild).
- Die Vogelperspektive oder Militärperspektive ist im einen Fall eine schiefe Parallelprojektion (s. Axonometrie), deren Bildtafel horizontal ist, d. h., alle ebenen horizontalen Figuren werden unverzerrt abgebildet (s. Bild) und im anderen Fall ist die Vogelperspektive eine Zentralprojektion, deren Augpunkt deutlich höher liegt als die größte Höhe des Objektes, und deren Bildtafel geneigt ist.
- Eine Ingenieurprojektion ist ein axonometrisches Bild mit einfachen Verkürzungen (0.5, 1, 1). Die Bilder der x- bzw. y-Achse schließen mit dem Bild der z-Achse Winkel von 132° bzw. 97° ein (s. Axonometrie). Ihre Vorteile sind: a) einfache Verkürzungen, b) gute Bildwirkung, c) (skalierte) Orthogonalprojektion, d) Umrisse von Kugeln sind Kreise.
- Eine Isometrie ist ein axonometrisches Bild, bei dem die Verzerrungen in x-, y- und z-Richtung alle gleich sind. Bei der Standardisometrie gilt außerdem: Die Bilder der Koordinatenachsen schneiden einander im Winkel von 120°. Eine typische Eigenschaft ist: In der Projektion eines achsenparallelen Würfels fallen zwei Punkte zusammen.
- Die Froschperspektive ist eine Zentralprojektion, deren Augpunkt nahe der Standebene liegt (s. Bild).
- Zentralperspektive ist eine Zentralprojektion.
- Perspektive wird oft als Kurzform für Zentralperspektive verwendet.
- Frontalperspektive ist eine Zentralprojektion eines Objektes mit drei wesentlichen zueinander orthogonalen Richtungen (z. B. Quader, Haus), wobei zwei dieser Richtungen parallel zur Bildtafel verlaufen und damit deren Fluchtpunkte im „Unendlichen“ liegen. Man nennt so eine Ansicht auch Perspektive mit einem Fluchtpunkt (s. Bild). Der eine besondere Fluchtpunkt ist in der Regel der Hauptpunkt. Der Vorteil einer Frontalperspektive: Alle ebenen Figuren in Ebenen parallel zur Bildtafel werden nur skaliert, aber unverzerrt, abgebildet (s. Beispiele: Brücke und Haus in Frontalperspektive).
- Perspektive mit zwei Fluchtpunkten ist eine Zentralprojektion, bei der die Fluchtpunkte zu zwei zueinander senkrechten orthogonalen Richtungen (meist horizontal) eine wesentliche Rolle spielen (s. Bild).
- Perspektive mit drei Fluchtpunkten ist eine Zentralprojektion bei der drei Fluchtpunkte eine wesentliche Rolle spielen. Hier ist die Bildtafel geneigt (s. Haus in Vogelperspektive der Zentralprojektion).
- Parallelperspektive ist eine Parallelprojektion.
- Polarperspektive ist eine frühere Bezeichnung für Zentralprojektion (s. Weblink Gangolf Delabar).
Ausbildung
Darstellende Geometrie ist heute ein Unterrichtsfach in technisch-berufsbildenden Schulen und ein grundlegendes Fach in der Ausbildung von Ingenieuren an einer Technischen Universität oder Fachhochschule.
Thema ist die Erfassung und Darstellung von räumlichen, insbesondere technischen Strukturen (geometrische Körper, Bauwerke, Darstellung des Geländes usw.).
Wichtigste Hilfsmittel sind Konstruktionszeichnungen, Perspektive (Zentralprojektion), Axonometrie, Kotierte Projektion und Ähnliches. Neben dem Erlernen von Zeichentechniken sollen die räumliche Vorstellungskraft und Ausdrucksweise gefördert sowie Querverbindungen zu Mathematik, zur Technik und zur Bildenden Kunst hergestellt werden.
Noch bis in die 2000er Jahre ein rein graphisches Fach (angewandtes geometrisches Zeichnen), ist es heute in weiten Bereichen eines der Computergrafik. In den letzten Jahren hatte die Bedeutung des Faches zwar nicht generell, aber in der Ausbildung abgenommen, weil die computergestützte Konstruktion (CAD) andere Fertigkeiten verlangt als die zeichnerische Darstellung von Hand.[1] Seit auch Schulen gut mit Computern im Unterricht ausgestattet sind, gehört das Fach wieder zu den bedeutendsten technischen Grundlagenausbildungen überhaupt und umfasst auch das Erlernen zugehöriger Programme – im Allgemeinen marktführender Spezial-CAD-Anwendungen der Branche.
Die eigentliche Denkarbeit, das Umsetzen der 2D-Darstellung (ob Papier oder Bildschirm) in ein 3D-(Denk-)Modell bleibt auch bei Benutzung von CAD dem Konstrukteur oder Entwerfer erhalten. Dagegen wird es schwieriger, räumliche Konstruktionsprobleme (z. B. Anschlussprofile bei schrägen Anschnitten) zu erkennen, wenn (und weil) man sich auf die Software verlässt.
„Darstellende Geometrie ist nicht in einem oberflächlichen Sinn Voraussetzung, ein CAD-Programm zu beherrschen. Sie zu üben, ist vielmehr eine Primärerfahrung, indem die räumliche Vorstellungskraft, das Abschätzen und Auswählen von Lösungsstrategien und die Präzision des Denkens trainiert werden.“
Zur Geschichte der Darstellenden Geometrie
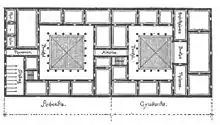
Bei der systematischen Errichtung von Bauwerken spielen Pläne mit konkreten Vorgaben eine wichtige Rolle. Schon im Altertum wurden Grund- und Aufrisse verwendet. Der älteste schriftliche Beleg dafür ist das Werk Zehn Bücher über Architektur des römischen Baumeisters Vitruvius. Aber erst Albrecht Dürer (1471–1528) schrieb in der Frühen Neuzeit das erste wirkliche Lehrbuch der Darstellenden Geometrie: Underweysung mit dem Zirkel und Richtscheydt[2] (Nürnberg 1525). Auf den Seiten 34–37 des ersten Buches treten auch schon die Kegelschnitte Ellipse, Parabel und Hyperbel auf. Gaspard Monge (1746–1818) führte in seinem Buch Geometrie descriptive[3] zum ersten Mal die strenge Zuordnung von Grund- und Aufriss ein, um räumliche Probleme zeichnerisch zu lösen. Die Grundaufgaben der Darstellenden Geometrie sind dort schon in der noch heute gebräuchlichen Fassung zu finden.
Die Grundlagen der Zentralprojektion waren schon den Griechen und Römern bekannt. Aber erst in der Renaissance wurde diese Art der Darstellung räumlicher Gegebenheiten durch die Malerei wiederentdeckt und zur Blüte weiterentwickelt. Siehe hierzu De pictura von Leon Battista Alberti (1404). Die Meister dieser Zeit waren Albrecht Dürer (1471–1528), Leonardo da Vinci (1452–1519) und Michelangelo (1475–1564).
Literatur
Das erste deutschsprachige Lehrbuch über Darstellende Geometrie stammt von Albrecht Dürer (1525). Nach dem Lehrbuch von G. Monge (1798) entstanden ab 1800 viele weitere Bücher in deutscher Sprache. Um Interessenten einen schnellen Überblick über aktuelle Literatur zu geben, werden hier zunächst neuere Bücher aufgeführt.
Nach 1950 erschienen:
- H. Brauner: Lehrbuch der Konstruktiven Geometrie. Springer-Verlag, Wien/ New York 1986, ISBN 3-211-81833-2.
- H. Brauner, W. Kickinger: Baugeometrie I, II. Bauverlag, Wiesbaden/ Berlin 1977, 1982, ISBN 3-7625-0825-9, ISBN 3-7625-2690-7.
- R. Fucke, K. Kirch, H. Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4.
- O. Giering, H. Seybold: Konstruktive Ingenieurgeometrie. C. Hanser Verlag, München/ Wien 1979, 1987, ISBN 3-446-14842-6.
- U. Graf, M. Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9.
- F. Hohenberg: Konstruktive Geometrie in der Technik. Springer-Verlag, Wien 1966, ISBN 3-211-80763-2.
- J. Hoschek, G. Spreitzer: Aufgaben zur darstellenden Geometrie. BI-Verlag, 1974, ISBN 3-411-01451-2.
- C. Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X.
- E. Müller, E. Kruppa: Lehrbuch der darstellenden Geometrie, Springer-Verlag, Wien, 1961, ISBN 978-3-211-80589-3.
- A. Pumann: Darstellende Geometrie. Teil 1 und Teil 2, Pumann, Coburg 1998, ISBN 3-9800531-0-5, ISBN 3-9800531-1-3.
- F. Rehbock: Darstellende Geometrie. Springer-Verlag, Berlin/ Göttingen/ Heidelberg 1969, ISBN 3-540-04557-0.
- F. Rehbock: Geometrische Perspektive. Springer-Verlag, Berlin/ Heidelberg/ New York 1980, ISBN 3-642-67542-5.
- F. Reutter: Darstellende Geometrie. I und II, Verlag G. Braun, Karlsruhe 1979, ISBN 3-7650-1201-7, ISBN 3-7650-2021-4.
- R. Stärk: Darstellende Geometrie. Schöningh-Verlag, 1978, ISBN 3-506-37443-5.
- K. Strubecker: Vorlesungen der Darstellenden Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967 (Online-Kopie).
- R. Thomae: Perspektive und Axonometrie. Springer-Verlag, 2013, ISBN 978-3-322-95328-5.
- K. Ulshöfer, D. Tilp: Darstellende Geometrie in systematischen Beispielen. Arbeitsblätter. Buchner, 2015, ISBN 978-3-7661-6092-8.
- W. Wunderlich: Darstellende Geometrie I (= Hochschultaschenbuch. 96/96a). Bibliograph. Inst., Mannheim 1966.
- W. Wunderlich: Darstellende Geometrie II (= Hochschultaschenb. 133/133a). Bibliograph. Inst., Mannheim 1967.
- U. Kurz, H. Wittel: Böttcher/Forberg Technisches Zeichnen. Springer-Vieweg, Wiesbaden 2014, ISBN 978-3-8348-1806-5.
- J. Hoschek, D. Lasser: Grundlagen der geometrischen Datenverarbeitung. Teubner-Verlag, Stuttgart 1989, ISBN 3-519-02962-6.
Vor 1950 erschienen:
- J. Adhemar: Darstellende Geometrie, Jent und Gassmann Verlag, Solothurn, 1845.
- P.B. Fischer: Darstellende Geometrie. Springer Fachmedien, Wiesbaden, 1921, ISBN 978-3-663-15478-5.
- J.T. Hjelmslev: Darstellende Geometrie, Leipzig, Berlin: B. G. Teubner, 1914, ISBN 587635130X.
- G. Loria: Vorlesungen über Darstellende Geometrie. 2 Bände. B.G. Teubner, Leipzig 1907.
- E. Müller: Lehrbuch der Darstellenden Geometrie für Technische Hochschulen.
- Erster Band. B. G. Teubner, Leipzig/ Berlin 1908.
- Zweiter Band. 2. Auflage. B. G. Teubner, Leipzig/ Berlin 1920.
- E. Müller: Vorlesungen über Darstellende Geometrie. 3 Bände. Franz Deuticke, Leipzig/ Wien 1923 1931.
- R. Müller: Leitfaden für die Vorlesungen über darstellende Geometrie an der Herzoglichen Technischen Hochschule zu Braunschweig. F. Vieweg, Braunschweig 1899.
- E. Papperitz: Darstellende Geometrie, in Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, Leipzig, B.G. Teubner-Verlag, 1907, 3. Band, S. 517–594. Göttinger Digi-Zentr.
- K. Pohlke: Zehn Tafeln zur darstellenden Geometrie. Gaertner-Verlag, Berlin 1876 (Google Books.)
- K. Rohn, E. Papperitz: Lehrbuch der Darstellenden Geometrie. 2 Bände. Leipzig 1893, 1896.
- G. Schaffnit: Geometrische Constructionslehre oder darstellende Geometrie: (Géométrie descriptive), Heyer-Verlag, Darmstadt, 1828.
- G. Schreiber: Spezielle darstellende Geometrie: für Architekten, Techniker, Mechaniker und Bauhandwerker, insbesondere für bau-, ploytechnische und höhere Gewerbeschulen, O. Spamer Verlag, Leipzig, 1865.
- G. Scheffers: Lehrbuch der darstellenden Geometrie. J. Springer, 1922.
- E. L. Stiefel: Lehrbuch der Darstellenden Geometrie. Springer-Verlag, Basel 1947, ISBN 978-3-0348-4098-9.
- C. Wiener: Lehrbuch der darstellenden Geometrie. 2 Bände. Teubner, Leipzig 1884, 1887, online auf archiv.org: Band 1, Band 2.
Weblinks
- Darstellende Geometrie für Architekten. (PDF; 1,5 MB). Skript (Uni Darmstadt).
- Darstellende Geometrie für Bauingenieure. (PDF; 974 kB). Skript (Uni Darmstadt).
- Grundlagen und Elemente der Verkehrsmaschinentechnik. (Memento vom 10. August 2013 im Internet Archive). (PDF; 493 kB). TU Dresden.
- Gangolf Delabar: Die Polar- und Parallelperspektive. 1893.
- COMPUTERunterstützte Darstellende und Konstruktive Geometrie. Uni Darmstadt (PDF; 3,4 MB).
- Geometry and Algorithms for COMPUTER AIDED DESIGN.
- H. Stachel: Die Geschichte der Darstellenden Geometrie in Österreich
Einzelnachweise
- PDF bei: igpm.rwth-aachen.de.
- Wikisource: Underweysung mit dem Zirkel und Richtscheydt.
- Geometrie descriptive.