Böschungsfläche
Schüttet man entlang eines Straßenrandes, der sich über einer Grundebene erhebt, Erde, so entsteht ein Böschungskörper, dessen Oberfläche Böschungsfläche genannt wird.
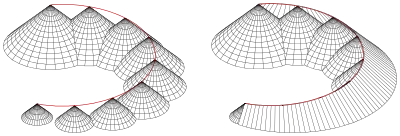

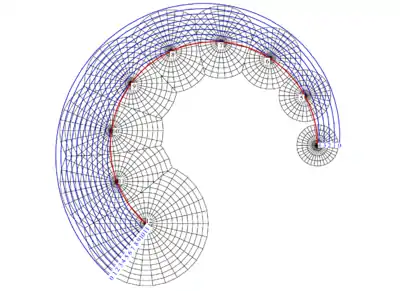
Mathematisch kann man sich eine Böschungsfläche als Einhüllende einer Schar von Kegeln (den Schüttkegeln) vorstellen, deren Spitzen sich auf einer vorgegebenen Kurve (Straßenrand) befinden, (siehe Figur 1). Die Böschungsfläche berührt jeden Kegel in einer Geraden. Solche Geraden heißen Falllinien. Um eine kotierte Projektion einer Böschungsfläche zu zeichnen, muss man Höhenlinien bestimmen. Da jede Höhenlinie jeden Kegel in einem Höhenkreis berührt, kann man sich eine Höhenlinie als Einhüllende einer Schar von (Höhen-)Kreisen von Kegeln vorstellen (siehe Figur 2). Dies ist der Schlüssel zum Zeichnen von Höhenlinien der Böschungsfläche in der zugehörigen kotierten Projektion (siehe Figur 3).
In der Praxis (siehe Figur 4) wird die Kurve (Straßenrand) kotiert gegeben, und die materialabhängige Steilheit der Schüttkegel bestimmt die zugehörigen Höhenkreise.
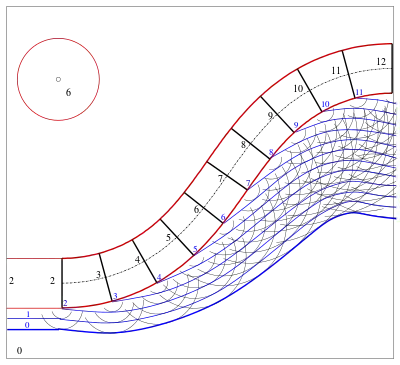
Die obigen Überlegungen lassen sich auch auf den Fall übertragen, bei dem kein Gelände aufgeschüttet wird, sondern abgetragen. Die dabei entstehende Böschungsfläche kann man als Einhüllende der Abtragungskegel auffassen. Auch in diesem Fall ergeben sich Höhenlinien als Einhüllende von Höhenkreisen (der Abtragungskegel).
In Büchern über Darstellende Geometrie werden Böschungsflächen zusammen mit Dachausmittlungen unter dem Oberbegriff kotierte Projektionen behandelt.
Quellen
- Fucke, Kirch, Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig, 1998, ISBN 3-446-00778-4, S. 139.
- Cornelie Leopold: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart, 2005, ISBN 3-17-018489-X, S. 193.
Weblinks
- Darstellende Geometrie für Bauingenieure (PDF; 1,2 MB). Skript (Uni Darmstadt)