Geodreieck
Das Geodreieck (eigentlich Geometrie-Dreieck) ist eine Kombination aus Lineal und Winkelmesser in Form eines rechtwinkligen, gleichschenkligen Dreiecks. Heute ist es vor allem ein Hilfsmittel für den Zeichen- und Mathematikunterricht, das dort speziell im Teilbereich Geometrie zum Messen und Zeichnen von Winkeln genutzt wird und das Zeichnen paralleler Geraden und einfacher Konstruktionen erleichtert. Es wird entgegen der Abbildung typisch mit der Hypotenuse nach oben gerichtet als Führungslineal für einen Bleistift verwendet. Die Beschriftung – außer die des Winkelmessers – erscheint dann aufrecht. Die cm-Teilung reicht von 0 in der Mitte beidseits bis 7 (cm), die unbeschriftete Unterteilung erfolgt in Millimeter mit einem etwas längerem Strich jeweils bei 5 mm. Die Hypotenuse ist etwa 15,5 cm lang.

Zur Verwendung bei großformatigeren Zeichnungen werden ähnliche jedoch um linear 50 % größere und steifere Dreiecke, häufiger mit Griff, unter der Bezeichnung TZ-Dreieck (TZ für Technisches Zeichnen) gefertigt. Diese sind an der Hypotenuse etwa 23 cm breit, die cm-Teilung läuft typisch beidseits bis 11.
Beschreibung
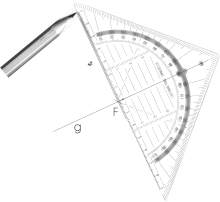

Geodreiecke gibt es mit und ohne Griff auf der Oberseite, mit und ohne erhabene Punkte an der Unterseite (sog. Tuschenoppen) sowie in unterschiedlichen Größen, die nach der Länge der Hypotenuse unterschieden werden. Diese längste Seite des Geodreiecks wird auch Linealkante genannt; sie trägt eine Zentimetereinteilung mit dem Nullpunkt in der Mitte. Dort beginnt die senkrecht zur Linealkante eingezeichnete Mittellinie, die das Zeichengerät in zwei Hälften teilt und die Höhe darstellt, mit deren Hilfe sich rechte Winkel genau zeichnen lassen. In das Dreieck sind zur Linealkante parallele Linien eingearbeitet. Entlang der Schenkel des Dreiecks sind Markierungen im Abstand eines Winkelgrades angebracht, die Gradeinteilung läuft von 0° bis 180° bzw. 180° bis 0°. Die Winkelskala erlaubt die Konstruktion eines Winkels mit der Genauigkeit etwa eines halben Grades.
Gezeichnet wird entlang der Linealkante. Insbesondere ist der rechte Winkel am Scheitelpunkt der Katheten des Geodreiecks zum Zeichnen ungeeignet; damit kann allenfalls die Rechtwinkeligkeit schnell überprüft werden. Zum Zeichnen von Orthogonalen und Loten dagegen legt man die Mittellinie auf die gegebene Gerade und zeichnet entlang der Linealkante. Beim Zeichnen von anderen Winkeln verfährt man entsprechend: Nullpunkt und Winkelmarkierung liegen auf dem gegebenen Schenkel, der freie Schenkel wird an der Linealkante gezeichnet.
Auf einigen Geodreiecken sind neben dem rechten und den halbrechten Winkeln die Winkel 7° und 42° (bzw. 138° und 173°) besonders markiert. Dies erleichtert eine axonometrische Darstellung nach ISO 5456-3 (Dimetrie).
Geschichte
Ein dem Geodreieck ähnliches Instrument wurde von den ägyptischen Geometern zu Beginn des dritten Jahrtausends v. Chr. als sog. Konstruktions-Remen verwendet für die nach den jährlichen Nilschwemmen notwendigen Feldvermessungen.
Das heute übliche Geodreieck aus durchsichtigem Kunststoff (PMMA oder PVC) wurde im Jahr 1964 in Wörgl von der Hamburger Firma Dennert & Pape Aristo – Werke unter dem Markennamen Aristo entwickelt.[1][2]
Varianten
Ein Geodreieck mit Griff und anderer Winkeleinteilung wird im Kartenbesteck für Aufgaben der Navigation benutzt und dort Kursdreieck genannt.
Geodreiecke werden auch zusammen mit einem Abschiebedreieck oder an einer Reißschiene eingesetzt.
Weblinks
- Historische Winkelmesser auf den Webseiten der Mathematikdidaktik der Uni Würzburg
Einzelnachweise
- ARISTO – Unternehmen / Geschichte. Abgerufen am 7. Februar 2013.
- Thomas Bergmayr: Das Geodreieck kommt aus Tirol in: Der Standard, Journal Nr. 9291, 11. September 2019, S. 15.