Umrisskonstruktion

In der Darstellenden Geometrie benutzt man zur Darstellung gekrümmter Flächen (Kugel, Zylinder, Rotationsflächen, …) den Umriss dieser Flächen. Unter dem Umriss kann man sich Flächenkurven vorstellen, die für einen Betrachter die Fläche von ihrer Umgebung trennen (siehe linkes Bild mit der Vase). Offensichtlich hängt der Umriss einer Fläche von der Art der Projektion (Sicht) ab. Für glatte Flächen (es gibt in jedem Punkt eine Tangentialebene) gilt: In einem Umrisspunkt einer Fläche ist der Projektionsstrahl eine Tangente an die Fläche. Bei Parallelprojektion ist die Projektionsrichtung in jedem Punkt gleich, bei Zentralprojektion (die Strahlen gehen durch einen festen Punkt, dem Augpunkt) hängt die Projektionsrichtung von dem zu projizierenden Punkt ab. Die Gesamtheit aller Umrisspunkte bildet die Umrisskurve (oder Umrisslinie) der Fläche. Zum Beispiel ist die Umrisskurve einer Kugel bei Parallelprojektion ein Großkreis (Kreismittelpunkt ist auch Kugelmittelpunkt). Bei Zentralprojektion ist der Umriss auch ein Kreis der Kugel, aber sein Mittelpunkt ist nicht der Kugelmittelpunkt (siehe Bild). In der Darstellenden Geometrie nennt man die Umrisskurve auf der Fläche den wahren Umriss. Die Projektion des wahren Umrisses ist eine ebene Kurve (in der Bildtafel) und heißt scheinbarer Umriss. Bei einer Parallelprojektion ist der wahre Umriss einer Kugel immer ein Großkreis. Bei senkrechter Parallelprojektion ist der scheinbare Umriss ein zum wahren Umriss kongruenter Kreis (die Radien sind gleich). Bei einer Vogelperspektive (schiefe Parallelprojektion, siehe Bild) ist der scheinbare Umriss eine Ellipse. Bei Zentralprojektion ist zwar der wahre Umriss in jedem Fall auch ein Kreis (vorausgesetzt der Augpunkt ist außerhalb der Kugel). Die Projektion dieses Kreises, also der scheinbare Umriss, kann wieder ein Kreis sein, aber nur, wenn der Mittelpunkt der Kugel auf der Lotgerade vom Augpunkt auf die Bildtafel liegt (siehe Bild). In allen anderen Fällen ist der scheinbare Umriss einer Kugel bei Zentralprojektion eine Ellipse. Je weiter der Kugelmittelpunkt von der Lotgerade entfernt ist, desto verzerrter ist der scheinbare Umriss.

Umriss: Vase bei senkrechter Parallelprojektion

wahrer u. scheinbarer Umriss einer Kugel bei senkrechter Parallelprojektion

wahrer u. scheinbarer Umriss einer Kugel bei Vogelperspektive (schiefe Parallelprojektion)

wahrer und scheinbarer Umriss einer Kugel bei Zentralprojektion

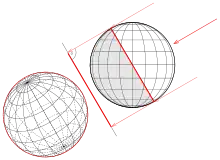
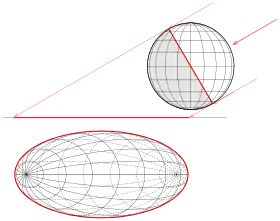
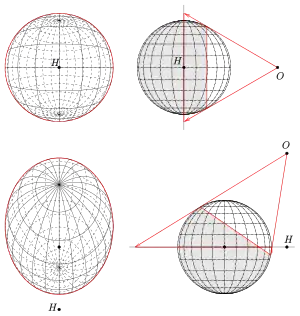
Wie das Beispiel mit der Vase zeigt, tragen nicht nur Punkte, in denen die Projektionsrichtung eine Tangentenrichtung ist, zum Umriss bei, sondern auch Randkurven (Deckel und Bodenkreis). Dies ist insbesondere bei der rechnerischen Bestimmung des Umrisses zu beachten. Zeichnerisch macht man das „automatisch“ richtig.

Eine gute Vorstellung vom wahren Umriss erhält man, wenn man sich die Fläche mit parallelem oder zentralem Licht beleuchtet vorstellt. Der wahre Umriss ist dann die Eigenschattengrenze auf der Fläche. Der scheinbare Umriss ist die Schlagschattengrenze der Fläche auf der Bildtafel.

Wie wir im Abschnitt Rechnerische bestimmung des Umrisses nachweisen, ist der wahre Umriss nicht nur bei der Kugel eine ebene Kurve, sondern bei allen Quadriken ist der wahre Umriss und damit als Projektion auch der scheinbare Umriss ein Kegelschnitt (Ellipse, Hyperbel, Parabel, …). Dass dies aber nicht generell der Fall ist, zeigen die Beispiele der Vase oder des Torus (siehe Bild). Rechnerisch ist im Allgemeinen die Bestimmung des Umrisses ein anspruchsvolles Problem und wird meistens mit geeigneten Algorithmen iterativ gelöst. In der klassischen Darstellenden Geometrie (mit Zirkel und Lineal) lassen sich für viele technisch wichtige Fälle (Kugel, Zylinder, Kegel, Torus, Rohrflächen, …) Umrisse bei senkrechter Parallelprojektion relativ leicht durch eine Approximation mit Hilfe eines Kurvenlineals bestimmen. Der Schlüssel für diese zeichnerische Approximation liegt im einfachen Umriss einer Kugel: Der Umriss einer Kugel ist bei senkrechter Parallelprojektion ein Kreis mit dem gleichen Radius. Der Umriss einer Fläche, die Einhüllende einer Schar von Kugeln (eventuell mit variablen Radien) ist, lässt sich als Einhüllende von Kreisen (Umrisse der Berührkugeln) zeichnerisch bestimmen (siehe Abschnitt Zeichnerische Bestimmung des Umrisses).

Bei einem Polyeder (siehe Bild mit Oktaeder und Ikosaeder) besteht der Umriss aus einem oder mehrerer Polygonzüge (zusammenhängende Strecken). Zeichnerisch lässt sich der Umriss eines Polyeders leicht intuitiv bestimmen. Wie man die Umrisskanten rechnerisch findet, wird unten erklärt.

Bemerkung: In manchen Büchern wird der wahre Umriss auch Kontur genannt.

Zeichnerische Bestimmung des Umrisses

Umrisskonstruktion für Zylinder u. Kegel (senkr. Parallelproj.)

Umriss eines Torus als Einhüllende von Berührkugeln (senkr. Parallelproj.)

Vase: Umrisskonstruktion mit Hilfe von Berührkugeln (senkr. Parallelproj.)

Umriss eines einsch. Hyperboloids als Einhüllende einer Geradenschar (senkr. Parallelproj.)

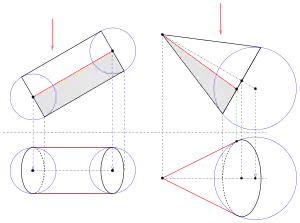
Wir gehen von einer Fläche aus, die sich als Einhüllende von Kugeln beschreiben lässt und wollen den Umriss für den Fall einer senkrechten Parallelprojektion in einer Zweitafelprojektion (Grund- und Aufriss) bestimmen.

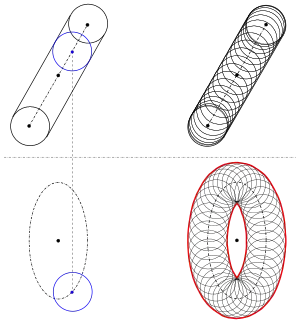
Beispiel Zylinder

Als erstes Beispiel wählen wir einen Zylinder, dessen Achse parallel zur Aufrisstafel verläuft. Der Aufriss erscheint also als Rechteck und ist damit leicht zu zeichnen. Damit ein anschauliches Bild im Grundriss entsteht, neigen wir die Zylinderachse. Den Zylinder fassen wir als Einhüllende einer Kugelschar auf, deren Mittelpunkte auf der Zylinderachse liegen und deren Radien konstant gleich dem Zylinderradius sind. Da der Umriss in diesem einfachen Fall aus zwei parallelen Strecken besteht, genügt es, zwei Berührkugeln (am Anfang und Ende, s. Bild) zu betrachten. Die Grundrisse der Kugelmittelpunkte sind leicht über Ordner zu finden. Die Umrisse dieser Kugeln sind zwei Kreise mit dem Radius des Zylinders. Die Einhüllenden Geraden ergeben den Grundriss des Umrisses. Ihre Aufrisse ergeben sich genauso einfach über Ordner. Als Umrissteile treten auch Teile des Bodens und Deckels (Ellipsenbögen) auf.

Beispiel Kegel

Damit der Aufriss des Kegels einfach zu zeichnen ist, wird die Kegelachse parallel zur Aufrisstafel gewählt. Den Kegel kann man sich als Einhüllende von Kugeln mit konstant zunehmenden Radien vorstellen. Die Umrissgeraden gehen durch die Kegelspitze und berühren die Berührkugel am Bodenkreis (s. Bild). Der Umriss dieser Berührkugel im Grundriss ist wieder ein Kreis ("Äquatorkreis"), dessen Mittelpunkt man über den zugehörigen Ordner auf dem Grundriss der Kegelachse findet. Die Tangenten an diesen Umrisskreis der Berührkugel (im Grundriss) durch die Kegelspitze ergeben die gesuchten Umrissstrecken des Kegels. Die Begrenzungen der Umrissstrecken im Aufriss ergeben sich entweder über Ordner aus dem Grundriss oder als Schnitt des "Äquatorkreises" (im Aufriss eine Strecke) der Berührkugel mit dem Boden Kreis des Kegels.

Beispiel Torus

Ein Torus lässt sich als Einhüllende einer Kugelschar mit Mittelpunkten auf einem Kreis und konstanten Radien auffassen. Damit der Aufriss des Torus einfach ist und der Grundriss ein anschauliches Bild liefert, wählen wir den Kreis der Kugelmittelpunkte senkrecht zur Aufrisstafel und gekippt gegenüber der Horizontalen (s. Bild). Der Umriss im Aufriss besteht aus zwei Halbkreisbögen und zwei parallelen Strecken (Hülle der Kugeln). Der Kreis der Mittelpunkte erscheint im Grundriss als Ellipse. Wir wählen eine genügende Anzahl von Berührkugeln durch die Wahl ihrer Mittelpunkte (im Grundriss) und zeichnen die zugehörigen Kugelumrisse (Kreise im Grundriss). Mit Hilfe eines Kurvenlineals oder "Freihand" ergibt sich als Einhüllende dieser Kreise der Umriss des Torus im Grundriss (rote Kurve). Er besteht aus zwei Teilen.

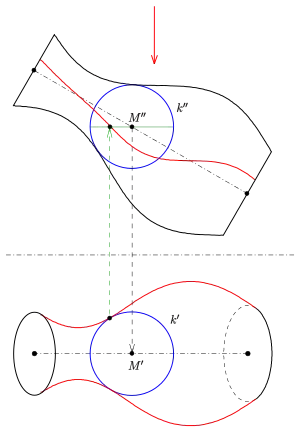
Beispiel Vase

Die Vase (s. Bild) ist eine Rotationsfläche. Sie entsteht durch Rotation der im Aufriss erkennbaren Kurven. Damit der Aufriss möglichst einfach ist, wählen wir wieder die Rotationsachse parallel zur Aufrisstafel und zur Senkrechten gekippt. Die Rotationsfläche lässt sich auch als Einhüllende einer Kugelschar, der Berührkugeln, mit variablen Radien auffassen. Konstruiert man genügend viele Berührkugeln (im Aufriss beginnend) und überträgt deren Mittelpunkte und Umrisse in den Grundriss, so ergibt sich der Umriss (im Grundriss) als Einhüllende der zugehörigen Kreise. Hat man den Umriss im Grundriss mit einem Kurvenlineal näherungsweise gezeichnet, so lässt sich für jede benutzte Berührkugel im Grundriss einen Umrisspunkt markieren, den man dann über einen Ordner auf den entsprechenden "Äquatorkreis" der Berührkugel im Aufriss übertragen kann. Auf diese Art erhält man auch den Aufriss des Umrisses (Eigenschattengrenze) der Vase.

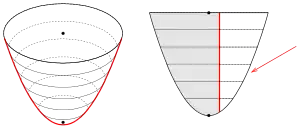
Beispiel einschaliges Hyperboloid

Ein Rotationshyperboloid lässt sich als Rotationsfläche durch eine geeignete Schar von Berührkugeln erzeugen. Da das einschalige Hyperboloid aber auch Geraden enthält und von einer ganzen Schar von Geraden überdeckt wird, hat man hier auch die Möglichkeit, genügend viele Strecken, deren Endpunkte auf dem Boden und Deckelkreis liegen, abzubilden. Die Einhüllenden dieser Strecken bilden dann den Umriss des Hyperboloids (s. Bild).

Rechnerische Bestimmung des Umrisses

Ebene Schnitte einer Kugel

Der ebene Schnitt einer Kugel ist entweder leer, besteht aus einem Punkt oder aus einem Kreis. Dies ist leicht einzusehen. Was man zur Berechnung von konkreten Punkten benötigt, ist eine Parameterdarstellung des Schnittkreises, falls ein Schnittkreis existiert (s. weblink CDKG, S. 88).

Gegeben: Kugel $K:x^{2}+y^{2}+z^{2}=r^{2},\quad r>0$ und Ebene $\varepsilon :{\vec {n}}\cdot {\vec {x}}=d$ Gesucht: Parameterdarstellung des Schnitteskreises $\varepsilon \cap K$ .

Der Abstand der Ebene $\varepsilon$ zum Mittelpunkt der Kugel ist $\delta ={\tfrac {|d|}{\|{\vec {n}}\|}}$ .

Falls

\delta >r

ist, ist der Schnitt leer.

Falls

\delta =r

ist, besteht der Schnitt aus einem Punkt.

Falls

\delta <r

ist, gibt es einen Schnittkreis.

a) Der Radius des Schnittkreises ist

\rho ={\sqrt {r^{2}-\delta ^{2}}}

.

b) Der Mittelpunkt ist

{\vec {f}}_{0}:={\tfrac {d}{{\vec {n}}^{2}}}{\vec {n}}

.

c) Im Folgenden sei

{\vec {n}}_{0}=(n_{x},n_{y},n_{z}):={\tfrac {\vec {n}}{\|{\vec {n}}\|}}

und

{\vec {f}}_{1}:=\rho (n_{y},-n_{x},0)/{\sqrt {n_{x}^{2}+n_{y}^{2}}}

, falls

|n_{x}|>0.5

oder

|n_{y}|>0.5

ist, andernfalls sei

{\vec {f}}_{1}:=\rho (0,n_{z},-n_{y})/{\sqrt {n_{y}^{2}+n_{z}^{2}}}

. (Diese Alternative garantiert eine fehlerfreie Wahl von

{\vec {f}}_{1}

.)

Ein zu

{\vec {f}}_{1}

senkrechter Radiusvektor ist

{\vec {f}}_{2}:={\vec {n}}_{0}\times {\vec {f}}_{1}

. Also ist

{\vec {x}}={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t

eine Parameterdarstellung des Schnittkreises.

Umriss einer Kugel

Umriss: Normalentest für glatte Flächen

Wir wissen, dass der wahre Umriss einer Kugel sowohl bei Parallelprojektion als auch bei Zentralprojektion ein Kreis ist. Jetzt soll für eine konkrete Projektion eine Parameterdarstellung des Umrisskreises bestimmt werden. Zunächst bei Parallelprojektion. Es muss hier nicht unterschieden werden zwischen senkrechter oder schiefer Parallelprojektion, da der wahre Umriss nur von der Projektionsrichtung abhängt.

Gegeben: Kugel $k:x^{2}+y^{2}+z^{2}=r^{2},\quad r>0$ und eine Parallelprojektion mit Richtung ${\vec {p}}$ .

Gesucht: Parameterdarstellung des wahren Umrisskreises.

Der wahre Umriss einer glatten Fläche trennt sichtbare Punkte von unsichtbaren Punkten. Ob ein Punkt sichtbar ist oder nicht, kann man mit Hilfe des Normalenvektors (s. unten) feststellen. Sichtbare und unsichtbare Punkte kann man nämlich am Vorzeichen des Skalarproduktes der Flächennormale mit der Projektionsrichtung erkennen. Punkte auf dem Umriss liefern das Skalarprodukt 0. Die zu lösende Aufgabe erinnert etwas an eine Extremwertaufgabe aus der Schule. Wie bei der Suche nach einem globalen Extremum darf man sich hier auch nicht auf die mit der Umrissbedingung gefundenen Punkte verlassen (s. Torus, unten). Sie könnten nur lokal Umrisspunkte sein. Außerdem muss man, wie bei der Extremwertaufgabe, auch Ränder gesondert miteinbeziehen (s. Vase oder Zylinder).

Für die Kugel ist eine Normale in einem Punkt $X:{\vec {x}}=(x,y,z)$ einfach der Ortsvektor dieses Punktes. Die Umrissbedingung im Punkt $X$ für die Projektionsrichtung ${\vec {p}}=(a,b,c)$ ist:

${\vec {x}}\cdot {\vec {p}}=ax+by+cz=0$

Dies ist die Gleichung einer Ebene durch den Mittelpunkt (= Nullpunkt) der Kugel. Mit der obigen Parameterdarstellung eines Ebenenschnitts einer Kugel lässt sich sowohl der wahre Umriss (im Raum) als auch nach der Projektion der scheinbare Umriss zeichnen. Bei der Projektion ist zu beachten, dass eine Parallelprojektion (senkrecht oder schief) immer eine lineare Abbildung darstellt. Deshalb wird der Kreismittelpunkt (des wahren Umrisses) auf den Mittelpunkt des Bildkreises/Bildellipse und ${\vec {f}}_{1},{\vec {f}}_{2}$ auf konjugierte Halbmesser der Bildellipse abgebildet.

Nun soll der Umriss einer Kugel bei Zentralprojektion bestimmt werden:

Gegeben: Kugel $k:x^{2}+y^{2}+z^{2}=r^{2},\ r>0$ und eine Zentralprojektion mit Augpunkt (Projektionszentrum) $O:{\vec {z}}=(u,v,w)$ .

Gesucht: Parameterdarstellung des wahren Umrisskreises.

Die Umrissbedingung für einen Punkt $X:{\vec {x}}=(x,y,z)$ ist:

${\vec {x}}\cdot ({\vec {x}}-{\vec {z}})={\vec {x}}^{2}-{\vec {x}}\cdot {\vec {z}}=x^{2}+y^{2}+z^{2}-ux-vy-wz$

=r^{2}-ux-vy-wz=0

.

Dies ist die Gleichung einer Ebene, die den Nullpunkt nicht enthält. Die Überlegungen zum Schnitt einer Kugel mit einer Ebene liefern auch in diesem Fall eine Parameterdarstellung des wahren Umrisskreises. Da eine Zentralprojektion keine lineare Abbildung ist, gilt die Aussage über Mittelpunkt und konjugierte Halbmesser hier nicht. Bei Zentralprojektion sollte man genügend Punkte des wahren Umrisskreises berechnen und diese einzeln projizieren und durch einen Polygonzug (in der Bildtafel) verbinden. Projektionsformeln für eine Zentralprojektion findet man im Artikel über Zentralprojektion.

Umriss eines Rotationsparaboloids

Umriss: Paraboloid bei senkrechter Parallelprojektion

Gegeben: Paraboloid $K:z=x^{2}+y^{2}$ und eine Parallelprojektion mit Richtung ${\vec {p}}=(a,b,c)$ .

Gesucht: der Umriss.

In diesem Fall ist ein Normalenvektor in einem Flächenpunkt nicht so einfach wie bei einer Kugel zu finden, aber stellt man das Paraboloid implizit durch $f(x,y,z)=x^{2}+y^{2}-z=0$ dar, so erhält man für einen Flächenpunkt $X:{\vec {x}}=(x,y,z)$ mit dem Gradienten $\nabla f=(f_{x},f_{y},f_{z})=(2x,2y,-1)$ einen Normalenvektor. Die Umrissbedingung lautet hier:

$\nabla f\cdot {\vec {p}}=(2x,2y,-1)\cdot (a,b,c)$

=2ax+2by-c=0

.

Dies ist die Gleichung einer senkrechten (zur Paraboloidachse parallele) Ebene. Der wahre Umriss ist also eine Parabel (s. Bild).

Mit Überlegungen zur Darstellung von ebenen Schnitten eines Paraboloids, wie wir sie oben für die Kugel angestellt haben, lässt sich eine Parameterdarstellung der Schnittparabel angeben (s. weblink CDKG, S. 94).

Bei einer Zentralprojektion mit Augpunkt (Projektionszentrum) $O:{\vec {z}}=(u,v,w)$ lautet die Umrissbedingung:.

$\nabla f\cdot ({\vec {x}}-{\vec {z}})=(2x,2y,-1)\cdot (x-u,y-v,z-w)=2(x^{2}+2y^{2})-z-2ux-2vy+w$

=-2ux-2vy+z+w=0

.

Dies ist die Gleichung einer Ebene, die nicht senkrecht steht. D.h. der wahre Umriss des Paraboloids ist bei Zentralprojektion (Augpunkt "außerhalb" des Paraboloids) eine Ellipse (s. weblink CDKG, S. 98).

Umriss eines einschaligen Rotationshyperboloids

Umriss: einsch. Hyperboloid, senkrechte Parallelprojektion

Gegeben: Hyperboloid $K:x^{2}+y^{2}-z^{2}=1$ und eine Parallelprojektion mit Richtung ${\vec {p}}=(a,b,c)$ .

Gesucht: der Umriss.

Wir verwenden wieder die implizite Darstellung: $f(x,y,z)=x^{2}+y^{2}-z^{2}-1=0$

Mit $\nabla f=(f_{x},f_{y},f_{z})=(2x,2y,-2z)$ lautet die Umrissbedingung:

$\nabla f\cdot {\vec {p}}=(2x,2y,-2z)\cdot (a,b,c)=2ax+2by-2cz=0$ .

Diese Gleichung beschreibt eine Ebene durch den Nullpunkt (Mittelpunkt des Hyperboloids). Im Gegensatz zur Umrissebene bei einer Kugel ist die Umrissebene hier nicht senkrecht zur Projektionsrichtung ! (s. weblink CDKG, S. 120).

Bei einer Zentralprojektion mit Augpunkt (Projektionszentrum) $O:{\vec {z}}=(u,v,w)$ lautet die Umrissbedingung:.

$\nabla f\cdot ({\vec {x}}-{\vec {z}})=(2x,2y,-2z)\cdot (x-u,y-v,z-w)=2(x^{2}+2y^{2}-z^{2})-2ux-2vy-2wz$

=-2ux-2vy+2wz+1=0

.

Dies ist die Gleichung einer Ebene, die nicht durch den Nullpunkt geht. Für eine Parameterdarstellung des wahren Umrisses müssen auch hier Überlegungen zu den möglichen ebenen Schnitten eines Hyperboloids gemacht werden (s. weblink CDKG, S. 121).

Umriss eines Torus

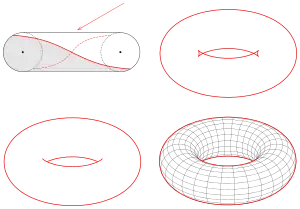
Umriss: Torus bei senkrechter Parallelprojektion

Ein Torus (Ringfläche) kann man sich durch Rotation eines Kreises um eine in der Kreisebene liegende Rotationsachse vorstellen. Aus dieser Vorstellung lässt sich eine Parameterdarstellung, die ähnlich zur Parameterdarstellung einer Kugel ist, ableiten. Um zu erkennen, dass der wahre Umriss kein ebener Schnitt ist, kann man (wie bei Paraboloid und Hyperboloid) eine implizite Darstellung verwenden:

f(x,y,z)=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0

.

Berechnet man hier die Umrissbedingung $\nabla f\cdot {\vec {n}}=0$ , so erkennt man, dass sie keine Ebenengleichung ist. Die Gleichung beschreibt eine Fläche 3. Ordnung (es kommen 3. Potenzen vor). Man kann sich also den wahren Umriss als Schnittkurve des Torus mit einer Fläche 3. Ordnung vorstellen. Wie man einzelne Punkte dieser Kurve berechnet, wird in weblink CDKG, S. 139 gezeigt.

Im Bild ist zu erkennen, dass die lokale Umrissbedingung zunächst Punkte liefert, die durch andere Flächenteile verdeckt werden. D.h., nach der Berechnung von Umrisspunkten aufgrund der Umrissbedingung, muss man hier noch für jeden vermeintlichen Umrisspunkt testen, ob er überhaupt sichtbar ist (s. weblink CDKG, S. 131).

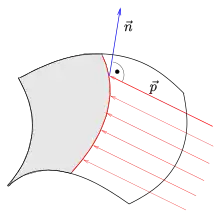
Umriss eines Polyeders

Umriss: Normalentest für Polyeder

Umriss: konvexe Polyeder (Oktaeder, Ikosaeder)

Umriss eines nicht konvexen Polyeders mit Punkte auf einem Torus

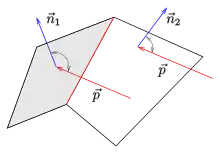
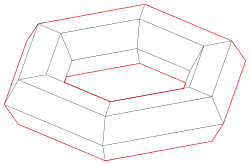
Bei einem Polyeder testet man mit dem Normalentest (s. Bild) jede (ebene) Teilfläche, ob sie sichtbar ist, und bestimmt anschließend die Kanten, die zu sichtbaren und unsichtbaren Teilflächen gehören. Diese Kanten bilden den wahren Umriss. Auch hier ist bei nicht konvexen Polyedern die wirkliche Sichtbarkeit mit einem Hiddenline-Algorithmus noch zu überprüfen (s. weblink CDKG, S. 163).

Literatur

Fucke, Kirch, Nickel: Darstellende Geometrie. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4. S. 165
Graf, Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9. S. 195
Leopold,C.: Geometrische Grundlagen der Architekturdarstellung. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X. S. 129

Weblinks

Darstellende Geometrie für Architekten (PDF; 1,5 MB). Skript (Uni Darmstadt)
CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt) (PDF; 3,4 MB), S. 87–142

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.