Rectifier (neuronale Netzwerke)

Im Kontext künstlicher neuronaler Netze ist ein Rectifier (auf deutsch: Gleichrichter) eine Aktivierungsfunktion eines künstlichen Neurons, die als Positivteil seines Arguments definiert ist:

f(x)=\max(0,x)

Rectifier Aktivierungsfunktion

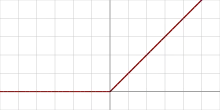
mit $x$ als Eingangswert des künstlichen Neurons.

Diese Aktivierungsfunktion wurde im Jahr 2000 von Hahnloser et al. mit starken biologischen Motivationen und mathematischen Begründungen erstmals bei dynamischen neuronalen Netzwerken eingeführt.[1] Rektifizierende Aktivierungsfunktionen wurden in der von Behnke vorgeschlagenen Neuronalen Abstraktionspyramide[2] genutzt, um spezifische Erregung und unspezifische Hemmung zu trennen. Diese hierarchische rekurrente konvolutionale Architektur wurde überwacht darauf trainiert, unterschiedliche Computer-Vision-Aufgaben iterativ zu lösen. Es wurde erstmals im Jahr 2011 nachgewiesen, dass ein Training tiefer Netzwerke mit rektifizierenden Aktivierungsfunktionen erfolgreicher ist als mit den vor dem Jahr 2011 weit verbreiteten Aktivierungsfunktionen wie z. B. der Sigmoidfunktion.[3] Rectifier sind aktuell (Stand 2019) die beliebtesten Aktivierungsfunktionen für tiefe neuronale Netze.[4] Eine Einheit, die den Rectifier verwendet, wird auch als rectified linear unit (ReLU) bezeichnet. Solche ReLUs finden Anwendung im Deep Learning, etwa im maschinellen Sehen[5] und der Spracherkennung.[6]

Einzelnachweise

Richard H. R. Hahnloser, Rahul Sarpeshkar u. a.: Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. In: Nature. 405, 2000, S. 947, doi:10.1038/35016072.
Sven Behnke: Hierarchical Neural Networks for Image Interpretation (= Lecture Notes in Computer Science), Band 2766. Springer, 2003, doi:10.1007/b11963.
Xavier Glorot, Antoine Bordes, Yoshua Bengio: Deep Sparse Rectifier Neural Networks. In: Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (= Proceedings of Machine Learning Research). Band 15. PMLR, Fort Lauderdale, FL, USA April 2011, S. 315–323 (mlr.press [PDF]).
Dan Becker: Rectified Linear Units (ReLU) in Deep Learning. In: Kaggle. Abgerufen am 19. November 2018 (englisch).
Xavier Glorot, Antoine Bordes and Yoshua Bengio: Deep sparse rectifier neural networks. 2011, abgerufen am 19. November 2018 (englisch).
László Tóth: Phone Recognition with Deep Sparse Rectifier Neural Networks. Abgerufen am 19. November 2018 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Richard H. R. Hahnloser, Rahul Sarpeshkar u. a.: Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. In: Nature. 405, 2000, S. 947, doi:10.1038/35016072.

[NeuralAbstractionPyramid-2] Sven Behnke: Hierarchical Neural Networks for Image Interpretation (= Lecture Notes in Computer Science), Band 2766. Springer, 2003, doi:10.1007/b11963.

[3] Xavier Glorot, Antoine Bordes, Yoshua Bengio: Deep Sparse Rectifier Neural Networks. In: Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (= Proceedings of Machine Learning Research). Band 15. PMLR, Fort Lauderdale, FL, USA April 2011, S. 315–323 (mlr.press [PDF]).

[4] Dan Becker: Rectified Linear Units (ReLU) in Deep Learning. In: Kaggle. Abgerufen am 19. November 2018 (englisch).

[5] Xavier Glorot, Antoine Bordes and Yoshua Bengio: Deep sparse rectifier neural networks. 2011, abgerufen am 19. November 2018 (englisch).

[6] László Tóth: Phone Recognition with Deep Sparse Rectifier Neural Networks. Abgerufen am 19. November 2018 (englisch).