1-aus-n-Code
Ein 1-aus-n-Code, auch One-Hot-Kodierung, stellt Zahlen binär dar, gewöhnlich für den Einsatz in der Digitaltechnik bzw. Computern.
| 1-aus-n-Code | |
|---|---|
| Stellenzahl | n |
| bewertbar | ja |
| stetig | ja |
| Gewicht | 1 |
| Minimaldistanz | 2 |
| Maximaldistanz | 2 |
| Hamming-Abstand | 2 |
| Redundanz | |
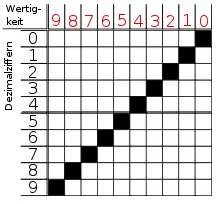
Eine dezimale Ziffer wird im 1-aus-n-Code durch n Bits dargestellt, wobei jeweils nur ein Bit auf 1 gesetzt ist, während die restlichen n-1 Bits 0 sind.
Der Hamming-Abstand beträgt 2, weshalb 1-Bit-Fehler bemerkt (indem man feststellt, ob die Quersumme genau 1 ist), aber nicht korrigiert werden können. 2-Bit-Fehler können nicht zuverlässig entdeckt werden.
Der Code ist sehr redundant, denn n Bit könnten bis zu verschiedene Zahlen kodieren.
Der 1-aus-n-Code findet Anwendung insbesondere bei der Steuerung von Zustandsautomaten, der Speicheradressierung, beim maschinellen Lernen sowie in Tastenfeldern, Anzeigetafeln, Maschinensteuerungen und früher auch Nixie-Röhren.
| Beispiel für 1-aus-n-Code mit n=10 | |||
|---|---|---|---|
| Dezimal- ziffer |
1-aus-10- codiert |
Binär- codiert | |
| 0 | 0000000001 | 0 0 0 0 | |
| 1 | 0000000010 | 0 0 0 1 | |
| 2 | 0000000100 | 0 0 1 0 | |
| 3 | 0000001000 | 0 0 1 1 | |
| 4 | 0000010000 | 0 1 0 0 | |
| 5 | 0000100000 | 0 1 0 1 | |
| 6 | 0001000000 | 0 1 1 0 | |
| 7 | 0010000000 | 0 1 1 1 | |
| 8 | 0100000000 | 1 0 0 0 | |
| 9 | 1000000000 | 1 0 0 1 | |
Andere Binärcodes
Literatur
- David Harris, Sarah Harris: Digital design and computer architecture. 2. Auflage. Morgan Kaufmann, San Francisco 2012, ISBN 978-0-12-394424-5, S. 129.