Zwölfeck

Das Zwölfeck oder Dodekagon ist eine geometrische Figur und ein Vieleck (Polygon) mit zwölf Ecken und zwölf Seiten.

Ein regelmäßiges Zwölfeck

Variationen

Das Zwölfeck ist darstellbar als:

• konkaves Zwölfeck, in dem mindestens ein Innenwinkel größer als 180° ist. Ein Zwölfeck kann höchstens sechs solche Winkel haben. Ein konkaves Zwölfeck kann regelmäßig oder unregelmäßig sein.
• konvexes Zwölfeck, in dem alle Innenwinkel kleiner als 180° sind. Ein konvexes Zwölfeck kann regelmäßig oder unregelmäßig sein.
• Sehnenzwölfeck, in dem alle Ecken auf einem gemeinsamen Umkreis liegen, aber die Seitenlängen (Sehnen) möglicherweise ungleich sind.
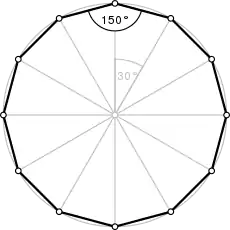
• regelmäßiges Zwölfeck, es ist bestimmt durch zwölf Punkte auf einem Umkreis. Die benachbarten Punkte haben zueinander stets den gleichen Abstand und sind mittels aneinandergereihten Seiten oder Kanten genannt, verbunden.
• regelmäßiges überschlagenes Zwölfeck, es ergibt sich, wenn beim Verbinden der zwölf Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

Es gibt nur einen regelmäßigen Zwölfstrahlstern, auch Dodekagramm genannt.

Die „Sterne“ mit den Symbolen {12/2} und {12/10} sind regelmäßige Sechsecke, {12/3} und {12/9} Quadrate sowie {12/4} und {12/8} gleichseitige Dreiecke.

• Beispiele für gleichseitige und unregelmäßige konkave Zwölfecke
• 
           gleichseitig
• 
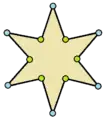           gleichseitig
• 
         unregelmäßig
• 
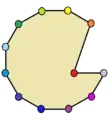         unregelmäßig

• Regelmäßiger Zwölfstrahlstern
• 
  :${\displaystyle \left\{12/5\right\}{,}\ \left\{12/7\right\}}$

Regelmäßiges Zwölfeck

Bei einem regelmäßigen Zwölfeck sind alle Seiten gleich lang und alle Eckpunkte liegen auf einem gemeinsamen Umkreis.

Formeln

Mathematische Formeln zum regelmäßigen Zwölfeck
Flächeninhalt	${\displaystyle A=(6+3\cdot {\sqrt {3}})\cdot a^{2}\approx 11{,}196\cdot a^{2}}$
	${\displaystyle A=(24-12\cdot {\sqrt {3}})\cdot r_{i}^{2}\approx 3{,}215\cdot r_{i}^{2}}$
	${\displaystyle A=3\cdot r_{u}^{2}}$
Länge der Diagonalen	${\displaystyle d_{2}={\frac {{\sqrt {6}}+{\sqrt {2}}}{2}}\cdot a\approx 1{,}932\cdot a}$
	${\displaystyle d_{3}=(1+{\sqrt {3}})\cdot a\approx 2{,}732\cdot a}$
	${\displaystyle d_{4}={\frac {{\sqrt {6}}+3\cdot {\sqrt {2}}}{2}}\cdot a\approx 3{,}346\cdot a}$
	${\displaystyle d_{5}=2\cdot r_{i}=(2+{\sqrt {3}})\cdot a\approx 3{,}732\cdot a}$
	${\displaystyle d=2\cdot r_{u}=({\sqrt {6}}+{\sqrt {2}})\cdot a\approx 3{,}864\cdot a}$
Inkreisradius	${\displaystyle r_{i}={\frac {2+{\sqrt {3}}}{2}}\cdot a\approx 1{,}866\cdot a}$
Umkreisradius	${\displaystyle r_{u}={\frac {{\sqrt {6}}+{\sqrt {2}}}{2}}\cdot a\approx 1{,}932\cdot a}$
Zentriwinkel	${\displaystyle \alpha ={\frac {360^{\circ }}{12}}=30^{\circ }}$
Innenwinkel	${\displaystyle \delta =180^{\circ }-\alpha =150^{\circ }}$

Konstruktion

Ein regelmäßiges Zwölfeck ist mit Zirkel und Lineal konstruierbar:

Zerlegung in regelmäßige Polygone

Das regelmäßige Zwölfeck ist außer dem regelmäßigen Sechseck das einzige regelmäßige Polygon, das sich vollständig in regelmäßige Polygone mit einer kleineren Zahl von Ecken zerlegen lässt:

• 
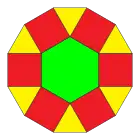
  Zerlegung in 6 gleichseitige Dreiecke, 6 Quadrate und   1 regelmäßiges Sechseck
• 
  Zerlegung in 12 gleichseitige Dreiecke und 6 Quadrate

Parkettierungen mit regelmäßigen Zwölfecken

Mit regelmäßigen Zwölfecken sind eine Vielzahl von Parkettierungen möglich. Die ersten zwei sind archimedische Parkettierungen, die dritte eine demireguläre Parkettierung:

• 
  3-12-12
• 
  4-6-12
• 
  3-3-4-12 und 3-3-3-3-3-3

Die Zahlen unter den Abbildungen geben an, wie viele Ecken die regelmäßigen Polygone haben, die jeweils an einem Punkt zusammenstoßen. Die Innenwinkel ergeben zusammen 360°. Diese Parkettierungen sind periodisch, drehsymmetrisch und translationssymmetrisch und enthält ausschließlich regelmäßige Polygone.

Ein Beispiel für eine kommerziell genutzte Parkettierung ist das Eternity-Puzzle, ein Legespiel, bei dem 209 unregelmäßige Polygonspielsteine zu einem Zwölfeck gelegt werden sollen.

Zwölfeck in der Numismatik

Threepence von 1942, Rückseite

Es gibt eine Vielzahl zwölfeckiger Münzen, z. B. das britische Threepence von 1942, die ehemalige 3–Pence–Münze aus Nigeria und die australische 50-cent-Münze, die 50-¢(= Seniti)-Münze von Tonga, sowie spezielle Sammlermünzen wie z. B. die spanische 300–Euro–Münze.

Zwölfeck in der Architektur

Vera Cruz Kirche in Segovia

Beispiele für zwölfeckige Gebäude sind:

Deutschland:

• das Panorama Kreuzigung Christi (Altötting)
• das Zwölfeckhaus in Dresden,
• Apostelkirche (Greding),
• das Schloss Großsachsenheim,
• viele der Hamburger Fahrradhäuschen,
• das Planetarium (Leipzig),
• der Dianatempel (ein zwölfeckiger Pavillon) in München,
• Zwölf-Apostel-Kirche (Mannheim),
• Reformations-Gedächtnis-Kirche (Nürnberg),
• der Wasserturm Schifferstadt,
• Wasserkunst Wismar
• die Gertrudenkapelle in Wolgast (Mecklenburg-Vorpommern)

Weitere:

• die Vera Cruz Kirche in Segovia,
• der Pavillon des Karussells von Vinohrady,
• der gläserne Kiosk der Tankstelle Auto Palace,
• die Pagode des Songyue-Tempels der Stadt Dengfeng,
• das Chorhaupt von St-Pierre-et-St-Paul de Maguelone, Grundriss aus halbiertem Zwölfeck

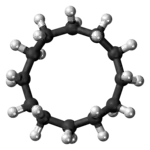
Zwölfeck in der Chemie

Molekülmodell von Cyclododecan

Molekülmodell von Phenalen

Das Molekülmodell von Cyclododecan ist nur in der Draufsicht zwölfeckig. Aus der dreidimensionalen Gestalt dieses Moleküls ergibt sich, dass die Kohlenstoffatome nicht alle in einer Ebene liegen. Außerdem befindet sich das Molekül bei höherer Temperatur in ständiger Bewegung, nämlich in Pseudorotation, d. h., es existieren eine Vielzahl von Konformationen.

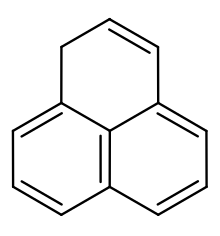
Ein gleichseitiges konkaves Zwölfeck wird vom Phenalen, einem polycyclischen aromatischen Kohlenwasserstoff, gebildet.

Weblinks

• Eric W. Weisstein: Dodecagon. In: MathWorld (englisch).

Einzelnachweise