Winkelmaß
Das Winkelmaß dient zur Angabe der Winkelweite eines ebenen Winkels in der Mathematik und als physikalische Größe. Je nach Einsatzgebiet werden verschiedene Maße und deren Einheiten verwendet.
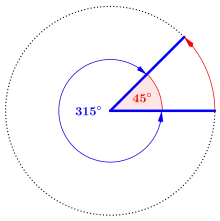
Auch auf gekrümmten Flächen wird das Winkelmaß verwendet. Hier misst man die Winkel in der Tangentialebene der Fläche – siehe auch sphärische Trigonometrie und sphärische Astronomie.
Gebräuchliche Winkelmaße
Lineare Unterteilung des Vollwinkels
Lineare Winkelmaße zeichnen sich dadurch aus, dass sie bei Drehung des Winkels erhalten bleiben, und bei einer Aufteilung einer Drehung in zwei Teildrehungen das Winkelmaß zur Gesamtdrehung gleich der Summe der Winkelmaße der Teildrehungen ist.
- Der Vollwinkel ist der kleinste Winkel, um den ein Strahl um seinen Ursprung gedreht wieder seine Ausgangsrichtung erreicht. Er ist eine gesetzliche Maßeinheit, für die kein Einheitenzeichen festgesetzt ist. Die Winkelweite wird als Vielfaches oder Teil angegeben, indem man dem Wort Vollwinkel einen Faktor als Zahlenwert voranstellt. Er ist auch umgangssprachlich und in der Mathematik in seiner impliziten Form sehr verbreitet, z. B. meint eine halbe Drehung eine Drehung um einen halben Vollwinkel. Man gibt also die Anzahl der gewünschten Umdrehungen an, die auch nicht-ganzzahlig sein darf.
- Im Gradmaß wird der Vollwinkel in 360 gleich große Teile unterteilt. Ein solcher Teil wird als ein Grad bezeichnet und mit dem Einheitenzeichen ° gekennzeichnet:
- 1 Vollwinkel = 360°
- Im Bogenmaß wird dem Vollwinkel die Maßzahl 2π zugewiesen. Der Teil des Vollwinkels heißt Radiant, Einheitenzeichen rad:
- 1 Vollwinkel = 2 rad
- Im geodätischen Winkelmaß wird der Vollwinkel in 400 gleich große Teile unterteilt. Ein solcher Teil wird als Gon bezeichnet und mit dem Einheitenzeichen „gon“ gekennzeichnet:
- 1 Vollwinkel = 400 gon
- Im Zeitmaß (Winkel) wird ein Vollwinkel in 24 Stunden unterteilt. Es wird in der Astronomie zur Angabe des Stundenwinkels und der Rektaszension verwendet:
- 1 Vollwinkel = 24h
- In Strich wird gemessen, indem der Vollwinkel in eine je nach Anwendungsgebiet unterschiedlich große Anzahl von gleich großen Teilen unterteilt wird:
- 1 Vollwinkel = 32¯ (nautisch)
- 1 Vollwinkel = 6400 mil (militärisch)
Nichtlineare Unterteilung des Vollwinkels
Ein anderes Messprinzip der Winkelweite erfolgt über das Verhältnis von Höhenunterschied zu Länge im Sinne eines Steigungswinkels, die Berechnung erfolgt über den Tangens des Winkels. Diese Skala ist nicht linear, d. h. bei Hintereinanderausführung zweier Drehungen entspricht die Winkelweite in diesem Maß im Allgemeinen nicht der Summe der Winkelweiten der einzelnen Drehungen. Für rechte Winkel geht die Steigung gegen unendlich. Die Länge kann nur positiv sein (es wird nur „nach vorne“ gemessen) und daher ist der Steigungswinkel nur im Bereich von −90° < α < +90° definiert.
- Prozent oder Promille (für Steigungen besonders im Verkehrswesen)
- ~0,57° → 1 %
- 1° → ~1,75 %
- 15° → 26,79… %
- 45° → 100 %
- 90° → ∞
- → 100 %
An Stelle eines (ebenen) Winkels kann man natürlich generell dieses Längenverhältnis zweier senkrecht zueinander stehender Strecken angeben. Dies entspricht dann immer dem Tangens des Winkels im zugrundeliegenden rechtwinkligen Dreieck. In der Luftfahrt gibt man so die Gleitzahl eines Flugzeuges an.
Die Entwicklung der Winkelmaße
Vollkreis und rechter Winkel
Prinzipiell kennen wir zwei Maßverkörperungen für die Winkelweite, die sich beide von einem intuitiven Bezugssystem von vorne, hinten, rechts und links ableiten.
- Den Kreis, der über das Konzept der Unterteilung in Kreissektoren, wie sie etwa als „Tortenstück“ geläufig ist, in enger Beziehung zum arithmetischen Prinzip der Bruchrechnung steht.
- Das Polygon, das über den Zusammenhang zwischen Innenwinkel und Zentriwinkel geometrischen Zugang zum Winkel ermöglicht. Hier ist insbesondere das Quadrat zu nennen, bei dem beide einen rechten Winkel bilden.
Daher gibt es zwei ausgezeichnete Maßeinheiten für den Winkel, den Vollwinkel (Vollkreis) und den rechten Winkel (Viertelkreis). Diese beide Konzepte finden sich schon in den frühesten Spuren protowissenschaftlicher Methoden früher Hochkulturen.[1]
Während der rechte Winkel heute nur insofern als Maß dient, sprachlich – und natürlich auch rechentechnisch – „gerade“ von „schiefen“ Winkeln zu unterscheiden und „spitze“ von „stumpfen“, also ein Prüfkriterium zur Zuordnung boolescher Werte („ja“, „nein“) ist, ist der Vollwinkel gesetzliche Maßeinheit. Bis etwa 1980 war aber auch der rechte Winkel als Rechter mit dem Einheitenzeichen ∟ in Deutschland üblich.
Bogenmaß: 2 π
Bei einem regelmäßigen Sechseck, dessen Ecken auf einem Kreis liegen, ergibt sich aus der Gleichheit von Kantenlänge und Umkreisradius eine Teilung des Sechsecks in sechs gleichseitige Dreiecke, sodass in ihm ausschließlich Winkel von sechzig Grad und deren Vielfache zu finden sind. Bei einem Radius des Umkreises von 1 beträgt der Umfang des Sechseckes 6. Dieser Wert wurde schon früh für den Kreisumfang als Wert angenommen und ist Bestandteil zahlreicher empirischer Formeln, die uns in alten Quellen überliefert sind.
Insbesondere aber die chinesischen Naturalisten der vorchristlichen Zeit setzen 3 kanonisch als Maßzahl des halben Kreisumfangs fest und entwickelten einen leistungsfähigen Kalkül der Winkelmessungen, und sie können insofern als Erfinder des Bogenmaßes angesehen werden.[2] Schon das Zhōu Bì Suàn Jīng chinesisch 周髀算经, W.-G. Chou pei suan ching, dessen Wurzeln auf etwa 1200 v. Chr. datiert werden, formuliert die Winkelberechnung elementarer Dreiecke über das Sechseck.[3] Diese durchaus vielversprechenden Ansätze verloren sich aber bald in einer komplizierten Numerologie und Zahlenmystik, die wissenschaftliche Weiterentwicklung durch Formalismen ersetzte und sich in einer Zehntelung des Kreises (Himmelsstämme) und einer Zwölftelung (Erdzweige) eher deren Anordnung und Symbolik als der mathematischen Anwendung widmete.[4]
Eingang in die moderne Mathematik findet das Bogenmaß mit dem exakten Wert erst im ausgehenden 17. Jahrhundert über den Differentialkalkül, da Formeln wie , die Eulersche Identität und die Näherungen (für kleine Winkel) nur gelten, wenn diese Funktionen mit Argumenten (Winkeln) im Bogenmaß verwendet werden. Dieses Winkelmaß ist damit die natürliche Einheit für das Argument der Sinus- und Cosinusfunktion, so wie e die natürliche Basis der Exponentialfunktion ist – für den Zusammenhang siehe komplexe Exponentialfunktion.
Gradmaß: 360, 400; Stundenmaß: 24
Ob es für die Entwicklung des Sexagesimalsystems eine Rolle spielte, dass sich in einen Kreis leicht ein regelmäßiges Sechseck mit Umfang des sechsfachen Radius einbeschreiben lässt, wissen wir nicht. Aber schon aus Sumerischer Zeit ist die Verwendung einer Sechzigerteilung wie auch einer Zwölferteilung für astrometrische Winkelmessungen nachweisbar. Die Letztere ist im Zodiak („Tierkreis“) erhalten.
Belegt ist die Einteilung des Vollwinkels in 360 Teile durch die frühen griechischen Astronomen. Sie dürfte wohl auf babylonische Tradition zurückzuführen sein. Hypsikles von Alexandria verwendet sie 170 v. Chr. im Anaphorikos.
Es sind die Astronomen, die diese Maßzahl für den Vollkreis schätzten, nicht nur der vielfältigen Teilungsmöglichkeiten wegen, sondern auch im Kontext der Kalenderrechnung: Zum einen nähert die Zahl die 365 Tage des Jahres an, insbesondere aber lassen sich auch die Berechnungen der Hauptstellungen des Mondes, also seiner synodischen Periode von knapp 30 Tagen und das Lunarjahr von 354 Tagen (360 − 6, im Zusammenhang mit 360 + 6) relativ zwanglos handhaben.
Die Möglichkeiten, die diese Rechenweise bietet, war für die jüdischen Gelehrten für die Berechnung des Neulichts – der Grundlage ihres Kalenders – entscheidend. Von ihnen wurde das Gradmaß als umfassendes Messprinzip für Winkel in Astronomie, Geodäsie und Geometrie etabliert, etwa auf Astrolabium, Sextant, oder Dioptra[5]. Es wurde auch in der westlichen Tradition ab dem 12. Jahrhundert weiterbehalten, wo das Grad seinen Namen bekommt. Die Methode umfasst auch die sexagesimale Teilung des gradus („Schritt“ am Kreis) in pars minuta prima „erster verminderter Teil“ und pars minuta secunda „nochmals verminderter Teil“, die Winkelangabe in Grad, Winkelminuten und Winkelsekunden. Selten findet sich auch noch die veraltete Tertie für „pars minuta tertia“ („dritter verminderter Teil“).
Daneben war seit lang vor der Zeitenwende die chronologische Einteilung des Tages – und damit auch des Vollkreises – in 24 oder 12 Stunden üblich (siehe dazu 24-Stunden-Zählung und 12-Stunden-Zählung). Im Kalenderwesen bezeichnet man das als die babylonischen oder griechischen (beginnend bei Sonnenaufgang) oder italienische Stunden (zuerst in jüdischer, dann islamische Tradition übergehend bei Sonnenuntergang). Der Sternkatalog des Hipparch von Nikaia (190–120 v. Chr.) ist im Almagest des Ptolemäus überliefert, seine trigonometrische Tabelle ist – darüber hinausgehend – mit einer verdoppelten, also 48er-Teilung (7,5°-Intervall) erstellt. Dasselbe System der Zwölfteilung findet sich aber auch in den chinesischen Erdzweigen, die – vermutlich auch auf mesopotamischer Tradition beruhend – etwa gleich alt sind wie der Hipparchkatalog[6] und sowohl für Zeitrechnung wie auch für Navigation genutzt wurden. Für Messungen in einem Maßsystem, das die Erdumdrehung widerspiegelt, ist die 24er-Teilung des Kreises als Zeitmaß bis heute üblich, weil es aus der Winkelangabe des Stundenwinkels eine direkte Zeitmessung ermöglicht. Ein Ursprung lässt sich nicht ausmachen, aber schon im 2. Jahrhundert v. Chr. erreicht – über Vermittlung der indischen Astronomie – eine 12-Stunden Zählung China (realisiert in den Erdzweigen).[4]
Die gemeinsame Wurzel dieser beiden Kreisteilungen zeigt sich im terrestrischen Längenwinkel (Längengrad), bei dem dem 360-Grad-Netz das der 24 Zeitzonen überlagert ist.
Die Schreibweise einer dezimale Angabe der Unterteilung eines Grades (mit Kommastellen) in Dezimalgrad ist erst Ende des Mittelalters in Arabien aufgekommen.
Obwohl die Geodäsie zu den Wissenschaftszweigen zählt, die an der Entwicklung des Gradmaßes ursächlich beteiligt waren, profitiert sie am wenigsten von der Zahl 360. In den 1790er Jahren wurde in Frankreich mit der Metrification begonnen, in deren Zuge das Urmeter als zehnmillionsten Teil des Meridianbogens vom Nordpol zum Äquator definiert wurde. In der Nouvelle Triangulation de la France wurde ein neues Gradnetz entwickelt, das den Kreis entsprechend in 400 Einheiten, die grade nouvelle (Neugrad) teilte, so dass 0,01gr einem Kilometer entsprach. Dieses geodätische Winkelmaß (in Gon) wird auch heute noch in der Geodäsie etwa für die Triangulation verwendet, obwohl sich die Definition des Meters schon lange nicht mehr auf die Länge des Erdmeridians bezieht.
Peilung: 32, 6400
Verdoppelt man den rechten Winkel (den Viertelkreis), erhält man einen Halbkreis, bei nochmaliger Verdoppelung einen Vollkreis. Wendet man diesen Gedankengang auf die Halbierung an, erhält man einen Achtelkreis, dann einen Sechzehntelkreis und so fort. Im Unterschied zu den vorherigen Systemen der Winkelbestimmung eignet sich dieses Verfahren insbesondere für Bezugsysteme in Bewegung (Azimutales Koordinatensystem), die das eingangs erwähnte Prinzip vier ausgezeichneter Richtungen im Bezug zur Blick- oder Fahrtrichtung repräsentieren, und daher den rechten Winkel als Grundmaß verwenden.
Verwendung fand das System insbesondere in der nautischen Navigation zur Peilung der Position und des Kurswinkels. Hierbei erfolgt eine Teilung in vier Hauptrichtungen („Voraus“, „Steuerbord“, „Achteraus“, „Backbord“), vier Nebenrichtungen (Achtel), und das Zweiunddreißigstel des Vollkreises wird mit der Maßeinheit Nautischer Strich bedacht. Erst in Kombination mit dem Kompass erhält diese Windrose eine ortsfeste Richtung (meistens den Norden) und wird zur Kompassrose. In der Schifffahrt wird aber heute üblicherweise auch im Gradmaß mit Dezimalminuten gepeilt.[7]
Ein weiterer Anwendungsbereich, bei der die Ausrichtung unabhängig von ortsfesten Netz entscheidend ist, ist das Visieren in der Artillerie. Aufgrund der hohen Präzision, die erforderlich ist – und einem rechentechnischen Vorteil in der Umwandlung von Visiereinteilung am Fadennetz in Entfernung des anvisierten Objekts – wird der Vollkreis in 6400 Artilleristische Striche (Schweizer Armee: Artilleriepromille, nordfest) eingeteilt.
Siehe auch
- Geschichte von Maßen und Gewichten
- zum Begriff eines Winkelmaßes in der synthetischen Geometrie siehe Euklidischer Körper.
Einzelnachweise
- Georges Ifrah: Universalgeschichte der Zahlen. Campus, Frankfurt am Main, New York 1986, 1991. Originaltitel: Histoire universelle des chiffres. dt. Alexander von Platen. ISBN 3-593-34192-1
- Die Zahl, S. 100ff. In: Marcel Granet: Das chinesische Denken. Übers. Manfred Porkert, Suhrkamp, Frankfurt 1993, ISBN 3-518-28119-4. Originaltitel: La pensée chinoise. Albin Michel, Paris 1936
- Granet, S. 201ff
- Die grundlegenden Ideen der chinesischen Wissenschaft, S. 163ff. In: Joseph Needham: Wissenschaft und Zivilisation in China. Band 1. Suhrkamp, Frankfurt am Main 1984. Originaltitel: The shorter science and civilisation in China. University Press, Cambridge 1978, dt. Rainer Herbster. ISBN 3-518-57692-5
- Die arabischen Zahlbuchstaben. Ifrah, S. 307ff
- Needham, S. 255
- Format international: ggg° mm.m’ – DIN 13 312 Navigation.