Stundenwinkel
Der Stundenwinkel und die Deklination sind die Koordinaten eines Gestirns im ortsfesten äquatorialen Koordinatensystem, mit denen dessen Position bezüglich eines Beobachtungsortes auf der Erde beschrieben werden kann. Der Name Stundenwinkel erklärt sich dadurch, dass er sich unter anderem für die Zeitmessung eignet; er wird deshalb auch meist im Zeitmaß statt im Gradmaß angegeben. Er entspricht jener Zeit, die seit dem letzten Durchgang des Gestirns durch den Meridian vergangen ist.

Definition
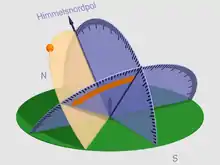
Der Stundenwinkel eines Himmelskörpers ist der Winkel zwischen zwei rechtwinklig zum Himmelsäquator stehenden Ebenen, der erdfesten Meridianebene am Ort des Beobachters und der Ebene des Stundenkreises des Himmelskörpers.
Der Stundenwinkel wird in der Ebene des Äquators vom Meridian aus in Richtung der scheinbaren täglichen Bewegung der Himmelskugel gemessen, also positiv in westlicher Richtung (für einen nach Süden blickenden Beobachter „nach rechts“) und negativ in östlicher Richtung („nach links“). Tritt ein Gestirn durch den Meridian, hat es in diesem Augenblick den Stundenwinkel Null.
Stundenwinkel einiger Himmelskörper
Die meisten Himmelskörper – im Besonderen die Sterne – bewegen sich am Himmel scheinbar westwärts. Ihr Stundenwinkel wächst stets in positiver Richtung an. Manche Erdsatelliten umkreisen die Erde von West nach Ost, wobei deren Stundenwinkel in negativer Richtung wächst. Der Stundenwinkel geostationärer Satelliten bleibt konstant.
Der Stundenwinkel eines Sterns wächst während eines siderischen Tages von ca. 23h 56m (gleich 24 Stunden Sternzeit) um 360°, in einer Stunde also um 15,04°. Da die Sonne sich bezüglich der Sterne um etwa ein Grad pro Tag in östlicher Richtung bewegt, wächst ihr Stundenwinkel etwas langsamer an als der eines Sterns. Er wächst im Mittel 15° pro Stunde (periodische kleine Abweichung vom Mittel: siehe Zeitgleichung). Dieser glatte Zahlenwert folgt aus der ursprünglichen Definition der Stunde als 1/24 eines Sonnentages, des Zeitraums zwischen zwei Meridiandurchgängen der Sonne, in welchem ihr Stundenwinkel um 360° wächst. Während 1/24 dieses Zeitraums wächst der Stundenwinkel um 360°/24 = 15°.
Auch der Stundenwinkel eines Sterns kann zur Zeitmessung verwendet werden. Er ist gleich der seit dem letzten Meridiandurchgang des Sterns verstrichenen Sternzeit.
Aufgrund der Eignung zur Zeitmessung wird der Stundenwinkel statt im Gradmaß oft auch im Zeitmaß (in Stunden, Minuten und Sekunden) angegeben (15° = 1 Stunde). Das gilt nicht nur für die Sonne, sondern auch für die Sterne. Bei der uns geläufigen Sonnenzeit geschieht eine Winkeländerung der Sonne von 15° in einer Stunde Sonnenzeit, bei der von Astronomen benutzten Sternzeit geschieht eine Winkeländerung eines Sterns von 15° in einer Stunde Sternzeit. Die in beiden Fällen verwendeten Zeitminuten und Zeitsekunden dürfen nicht verwechselt werden mit den Bogenminuten und den Bogensekunden eines im Gradmaß gegebenen Winkels.
Stundenwinkel und äquatoriale Montierung
Äquatoriale Montierungen von astronomischen Beobachtungsinstrumenten ermöglichen die getrennte Messung der ortsfesten äquatorialen Koordinaten Stundenwinkel und Deklination. Sie besitzen je eine Drehachse, um der Änderung der beiden Koordinaten zu folgen. Ändert sich der Stundenwinkel gleichmäßig wie bei Sternen, so lässt sich das Instrument automatisch durch einen Antrieb an der zur Himmelsachse parallelen Rektaszensionsachse (oder Stundenachse) den Gestirnen nachführen. Weil sich die Deklination der Sterne nicht ändert, kann bei deren Beobachtung die Deklinationsachse arretiert werden.
Meist besitzt die Stunden- und die Deklinationsachse der Montierung eine Feinbewegung, um kleine Abweichungen der Nachführung – vor allem bei langbelichteter Astrofotografie – korrigieren zu können. Dafür wird ein heller Stern am Fadennetz eines Leitfernrohrs beobachtet. Bei Go-to-Montierungen kann das mit dem Handcomputer oder mittels CCD-Sensor erfolgen.
Stundenwinkel und Rektaszension
Stundenwinkel und Rektaszension sind die einander entsprechenden Koordinaten im ortsfesten beziehungsweise im rotierenden äquatorialen Koordinatensystem. Bezugsebene des Rektaszensions-Winkels ist nicht die ortsfeste Meridianebene, sondern die rotierende Ebene, die vom Großkreis durch den Frühlingspunkt und die Himmelspole aufgespannt wird. Die Rektaszension wird positiv in östlicher Richtung – also entgegengesetzt zum Stundenwinkel – gezählt. Die Deklination ist in beiden Systemen identisch, denn sie bezieht sich beide Male auf die Äquatorebene.
Der Stundenwinkel ergibt sich aus der Differenz der Sternzeit und der Rektaszension
- .
Der Stundenwinkel des Frühlingspunkts ist identisch mit der Sternzeit am Standort. Er ist null, wenn der fiktive Frühlingspunkt den (örtlichen) Meridian passiert. In diesem Moment sind Stundenwinkel und Rektaszension für alle Himmelskörper gleich groß, unterschiedlich sind nur die Vorzeichen.
Die Umrechnung zwischen Stundenwinkel und Rektaszension ist unter anderem im Hauptartikel Astronomische Koordinatensysteme beschrieben.
Siehe auch
- Astronomische Koordinatensysteme zur genaueren Erläuterung verschiedener Himmelskoordinaten
- Nautisches Dreieck zur Umrechnung zwischen verschiedenen Koordinatensystemen
- Sphärische Astronomie
- Ortsstundenwinkel
- Parallaktischer Winkel
- Sternbahn