Disklination
Eine Disklination ist ein Gitterfehler (Defekt) in einem Kristall, bei dem die Rotationssymmetrie (Orientierungsordnung) verletzt wird.
Die Disklination stellt das Analogon zur Dislokation dar, bei der die Translationssymmetrie (Translationsordnung) verletzt wird.
Beispiel in 2 Dimensionen
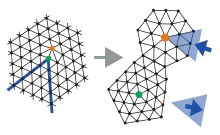
Disklinationen und Dislokationen sind topologische Defekte und spielen eine zentrale Rolle bei der Beschreibung des Schmelzens eines zweidimensionalen Kristalls durch die die KTHNY-Theorie.
In zwei Dimensionen bildet die dichteste Packung gleich großer Scheiben (Kugeln, Teilchen, Atomen) einen hexagonalen Kristall, d. h. jede Scheibe hat sechs nächste Nachbarn. Lokale Verzerrungen und Verdrillungen des Kristalls bilden Konfigurationen, in der eine Scheibe eine andere Koordinationszahl, d. h. Anzahl von Nachbarn, hat, typischerweise fünf oder sieben.
Da Disklinationen topologische Defekte sind, können sie nur paarweise entstehen, sodass – bis auf Randeffekte – immer genauso viel 5er- wie 7er-Disklinationen vorhanden sind. Ein „gebundenes“ 5-7-Paar stellt eine Dislokation dar. Sind isolierte Disklinationen in einer Monolage vorhanden, die z. B. durch thermische Fluktuationen entstanden sind, so handelt es sich um eine im zeitlichen Mittel isotrope Flüssigkeit in zwei Dimensionen; ein zweidimensionaler Kristall ist frei von Disklinationen.
Bei der 7er-Disklination (orange im Bild dargestellt) wird ein „Kuchenstück“ (blaues Dreieck) hinzugefügt, während bei der 5er-Disklination eines entfernt wird. Derart zerstören viele Disklinationen die Orientierungsordnung, während Dislokationen nur die Translationsordnung stören, da zusätzliche Gitterlinien eingefügt werden (blaue Linien).
Eine einzelne Disklination ist ein topologischer Defekt, da sie nicht durch eine lokale, affine Transformation hergestellt werden kann. Das bedeutet, dass sie nicht einzeln hergestellt werden kann, ohne den hexagonalen Kristall bis ins Unendliche, mindestens aber bis zu seinem Rand, aufzuschneiden, um ein „Kuchenstück“ einzufügen bzw. zu entfernen. In einem hexagonalen Kristall hätten die Kuchenstücke ursprünglich eine Spitze mit einem Winkel von 60°. Die Dehnung auf 72° bei einer 5er-Disklination und die Stauchung auf ca. 51,4° bei einer 7er-Disklination bedeutet, dass Disklinationen elastische Energie kosten.
Siehe auch
Literatur
- J. M. Kosterlitz und D. J. Thouless: Ordering Metastability, and Phase Transitions in Two-Dimensional Systems. In: Journal of Physics C. Band 6, 1973, S. 1181
- D. R. Nelson und B. I. Halperin: Dislocation-mediated melting in two dimensions. In: Physical Review B. Band 19, 1979, S. 2457–2484
- A. P. Young: Melting and the vector Coulomb gas in two dimensions. In: Physical Review B. Band 19, 1979, S. 1855–1866
- U. Gasser, C. Eisenmann, G. Maret, P. Keim: Melting of crystals in two dimensions - mini review. In: ChemPhysChem, Band 11/5, 2010, S. (2010)
- Nabarro: Theory of crystal dislocations. Oxford University Press 1967