Quergleiten
Das Quergleiten ist der Prozess, bei dem sich eine Schraubenversetzung aufgrund lokaler Spannungen von einer Gleitebene in eine andere bewegt. Er ermöglicht eine nicht-planare Bewegung von Schraubenversetzungen.
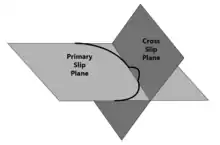
Dagegen wird die nicht-planare Bewegung von Kantenversetzungen durch Steigen erreicht.
Da der Burgersvektor einer perfekten Schraubenversetzung parallel zur Versetzungslinie verläuft, hat sie eine unendliche Anzahl von möglichen Gleitebenen (Ebenen, die die Versetzungslinie und den Burgersvektor enthalten), im Gegensatz zu einer Kanten- oder Mischversetzung, die eine einzige Gleitebene hat. Daher kann eine Schraubenversetzung entlang jeder Ebene gleiten, die ihren Burgersvektor enthält. Während des Quergleitens wechselt die Schraubenversetzung vom Gleiten entlang einer Gleitebene zum Gleiten entlang einer anderen Gleitebene, die als Quergleitebene bezeichnet wird. Das Quergleiten von sich bewegenden Versetzungen kann durch Transmissionselektronenmikroskopie veranschaulicht werden.[1]
Mechanismus
Die möglichen Quergleitebenen werden durch das Kristallsystem bestimmt.
In kubisch-raumzentrierten (krz) Metallen kann eine Schraubenversetzung mit b=0,5<111> auf {110}-Ebenen oder {211}-Ebenen gleiten.
In kubisch flächenzentrierten (kfz) Metallen können Schraubenversetzungen von einer {111}-Typ-Ebene zu einer anderen gleiten. In kfz-Gittern dissoziieren reine Schraubenversetzungen jedoch in zwei gemischte Teilversetzungen auf einer {111}-Ebene, und die erweiterte Schraubenversetzung kann nur auf der Ebene gleiten, welche beide Teilversetzungen enthält.[2]
Um das Quergleiten von Teilversetzungen in kfz-Metallen zu erklären, sind zwei Mechanismen postuliert:
- Beim Friedel-Escaig-Mechanismus ziehen sich die beiden Teilversetzungen zu einem Punkt zusammen und bilden eine perfekte Schraubenversetzung auf ihrer ursprünglichen Gleitebene. Dann dissoziieren sie wieder auf der Quergleitebene, wodurch zwei verschiedene Teilversetzungen entstehen. Scherspannungen können dann dazu führen, dass sich die Versetzung ausdehnt und auf die Quergleitebene bewegt.[3] Molekulardynamische Simulationen haben den Friedel-Escaig-Mechanismus bestätigt.[4]
- Alternativ wird beim Fleischer-Mechanismus eine Teilversetzung auf die Quergleitebene emittiert; danach ziehen sich die beiden Teilversetzungen auf der Quergleitebene zusammen, wodurch eine Treppenversetzung entsteht. Dann verbindet sich die andere Teilversetzung mit der Treppenversetzung, so dass sich beide Teilversetzungen auf der Quergleitebene befinden. Da die Treppenversetzung und die neuen Teilversetzungen hochenergetisch sind, würde dieser Mechanismus sehr hohe Spannungen erfordern.[2]
Bedeutung in der Plastizität
Das Quergleiten ist von Bedeutung für die Plastizität, weil dadurch zusätzliche Gleitebenen aktiv werden und Schraubenversetzungen Hindernisse umgehen können. Schraubenversetzungen können sich in ihrer primären Gleitebene (d. h. in der Ebene mit der höchsten aufgelösten Schubspannung) um Hindernisse herum bewegen. Eine Schraubenversetzung kann auf eine andere Gleitebene gleiten, bis sie das Hindernis passiert hat, und dann zur primären Gleitebene zurückkehren.[2] Schraubenversetzungen können dann Hindernisse durch konservative Bewegung (ohne atomare Diffusion) vermeiden, im Gegensatz zu Kantenversetzungen, die klettern müssen, um sich um Hindernisse herum zu bewegen. Daher sind einige Methoden zur Erhöhung der Fließspannung eines Werkstoffes, z. B. die Mischkristallverfestigung, weniger effektiv, da sie aufgrund von Quergleiten die Bewegung von Schraubenversetzungen nicht blockieren.[5]
Bei hohen Dehnungsraten (während der Phase II der Kaltverfestigung) haben Simulationen der diskreten Versetzungsdynamik (DD) nahegelegt, dass Quergleiten die Erzeugung von Versetzungen fördert und die Versetzungsgeschwindigkeit in einer Weise erhöht, die von der Dehnungsrate abhängig ist, was eine Verringerung der Fließspannung und der Kaltverfestigung zur Folge hat.[6]
Quergleiten spielt auch eine wichtige Rolle bei der dynamischen Erholung (Stufe III der Kaltverfestigung), indem er die Annihilation von Schraubenversetzungen und dann die Bewegung von Schraubenversetzungen in eine Anordnung mit niedrigerer Energie fördert.
Siehe auch
Einzelnachweise
- Bacon, D. J.: Introduction to dislocations. 5th ed Auflage. Butterworth-Heinemann, Oxford 2011, ISBN 978-0-08-096672-4.
- Nix, William D.,, Materials Research Society.: Imperfections in crystalline solids. Cambridge, United Kingdom, ISBN 1-107-12313-5.
- D. Caillard, J. L. Martin: Some aspects of cross-slip mechanisms in metals and alloys. In: Journal de Physique. 50, Nr. 18, 1989, ISSN 0302-0738, S. 2455–2473. doi:10.1051/jphys:0198900500180245500.
- T. Rasmussen, K. W. Jacobsen: Atomistic Determination of Cross-Slip Pathway and Energetics. In: Physical Review Letters. 79, Nr. 19, 10. November 1997, S. 3676–3679. doi:10.1103/PhysRevLett.79.3676.
- Courtney, Thomas H.: Mechanical Behavior of Materials. 2nd ed. Reimp. McGraw Hill Education (India), New Delhi 2013, ISBN 1-259-02751-1.
- Z. Q. Wang, I. J. Beyerlein, R. LeSar: The importance of cross-slip in high-rate deformation. In: Modelling and Simulation in Materials Science and Engineering. 15, Nr. 6, 1. September 2007, ISSN 0965-0393, S. 675–690. bibcode:2007MSMSE..15..675W. doi:10.1088/0965-0393/15/6/006.