Räuber-Beute-Beziehung
Mit Räuber-Beute-Beziehung oder seltener Räuber-Beute-Verhältnis wird die dynamische Wechselwirkung zwischen einer Räuber- und einer Beutepopulation über längere Zeiträume beschrieben. Es handelt sich um ein vereinfachendes Modell eines Ausschnitts der Nahrungsnetze, die im biologischen Fachgebiet Ökologie analysiert werden. Räuber-Beute-Beziehungen lassen sich mathematisch darstellen und können in begrenztem Maß zur Vorhersage zukünftiger Populationsentwicklungen genutzt werden.
Abgrenzung
Räuber-Beute-Beziehungen stellen einen Ausschnitt einer Nahrungskette aus einem der Nahrungsnetze dar, die ein Forschungsgegenstand des Fachgebiets Ökologie sind. Der Fachbegriff des Räubers im weiteren Sinne umfasst neben den echten Beutegreifern auch Parasiten und Parasitoide sowie Weidegänger in ihrer Funktion als Konsumenten pflanzlicher Nahrung. Die unten beschriebenen Modellbildungen können auf alle vier Fälle angewendet werden. Mit dem Modell können dagegen keine Populationsentwicklungen von Arten betrachtet werden, die sich von toter organischer Substanz ernähren, denn bei Populationsschwankungen von Aasfressern, Detritusfressern und Destruenten ist keine Größenänderung einer Beutepopulation zu erwarten.
In der Natur existieren zahlreiche komplexe Reaktionsmuster in den Beziehungen zwischen Räuber und Beute, ihre Erklärung bildet ein wesentliches, zentrales Gebiet der ökologischen Theorie. Aufgrund der Vielfalt der unterschiedlichen Beziehungen ist die Übertragung von einem System auf ein anderes schwierig. In manchen Fällen dezimiert ein Räuber eine Beutetierpopulation auf einen Bruchteil ihrer unbeeinflussten Dichte, in anderen Fällen ist der Einfluss eines Räubers auf eine Beutepopulation kaum nachweisbar. Wesentlich ist hierbei zum einen, ob ein Räuber auf eine bestimmte Beuteart spezialisiert ist, oder ob es sich um einen Generalisten mit zahlreichen gleichwertigen Beutearten handelt. Zwischen diesen beiden Extremen existiert ein breites Spektrum von Fällen unterschiedlicher Präferenz. Zum anderen sind stets Auswirkungen anderer Arten und Wechselwirkungen mit den Umweltfaktoren bedeutsam.
Besonders interessant für die ökologische Analyse sind Systeme, in denen der Räuber die Dichte seiner Beute reguliert, oder in denen die Dichte von beiden zyklischen Schwankungen unterliegt. In der Regel beeinflussen dabei zahlreiche weitere Faktoren wie Nahrungsangebot,[1] Klima, Habitat-Konkurrenz, Krankheitserreger, Parasiten, Stress und andere Räuber ebenfalls die Populationsgrößen (siehe auch Populationsdynamik).
Mit dem Ziel, allgemeine dynamische Eigenschaften von Räuber-Beute-Beziehungen darzustellen und zu untersuchen, wurden in der theoretischen Biologie verschiedene mathematische Modelle erstellt. Am einfachsten und bekanntesten ist das Lotka-Volterra-Modell. Grundlage sind die Arbeiten des österreichischen Mathematikers Alfred J. Lotka und des italienischen Mathematikers und Physikers Vito Volterra, die 1925 und 1926 unabhängig die heute nach ihnen benannten Lotka-Volterra-Gleichungen formulierten. Es handelt sich um mathematische Differentialgleichungen, in denen erstmals der quantitative Aspekt der Populationsentwicklung in Abhängigkeit von der Zeit dargestellt wurde. Sie beruhen auf der logistischen Gleichung. Die biologischen Anwendungen dieser Gleichungen sind heute unter dem Namen der ersten, zweiten und dritten Lotka-Volterra-Regel bekannt.
Eine Computersimulation, welche die Räuber-Beute-Beziehung anschaulich macht, ist die Simulation Wator von Alexander K. Dewdney und David Wiseman.
In der Räuber-Beute-Dynamik sind häufig ausgeprägte Schwankungen der Populationsdichten zu beobachten, die langfristig um einen Mittelwert pendeln.[2] Bei einer Bestandsregulierung durch den Menschen hingegen wird starken Schwankungen vorgebeugt und man strebt nach Möglichkeit stabile Populationsdichten an.
Das Lotka-Volterra-Modell
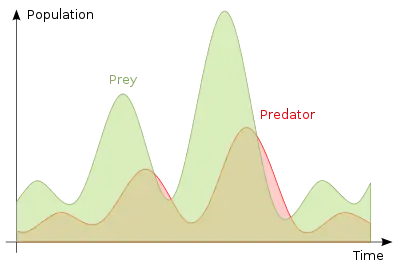
Im Lotka-Volterra-Modell zeigen Räuber- und Beutearten gekoppelte Häufigkeitsschwankungen. Ein reiches Angebot an Nahrung bzw. Beutetieren ermöglicht es den Räubern, viele Nachkommen großzuziehen, so dass die Räuberpopulation wächst. Durch die größere Populationsdichte bei den Räubern kommt es zu einer Dezimierung der Beutepopulation und damit zu einem mangelhaften Nahrungsangebot für die Räuber, so dass weniger oder keine Jungtiere mehr großgezogen werden können und schwache erwachsene Räuber verhungern. Dieser Rückgang der Räuberpopulation ermöglicht es nun der Beutepopulation sich zu erholen und der periodische Ablauf beginnt von vorn.
Im Modell handelt es sich allerdings um sogenannte neutral stabile Zyklen. Das bedeutet: Die Zyklen entstehen ohne äußere Einwirkungen, die Zykluslänge ergibt sich aus der Wahl der Variablen (ohne Zeitgeber), ohne Störungen von außen würden diese Zyklen ohne jede Abweichung für immer weiterlaufen. Aber: In natürlichen Systemen tatsächlich beobachtbare Zyklen können normalerweise aufgrund dieses Mechanismus nicht entstehen, aufgrund der unvermeidlich und immer einwirkenden Schwankungen der Umweltvariablen würden Populationen, die der Modelldynamik unterliegen, in der Realität azyklisch und erratisch fluktuieren. Populationen, deren Schwankungen ausschließlich durch das Modell erklärt werden könnten, gibt es vermutlich nicht. Dennoch ist das Modell als erste Näherung zur Erklärung gekoppelter Schwankungen der Populationsdichte nützlich.
Der berühmteste Fall, bei dem für die Population eines Räubers und seiner Beute gekoppelte, zeitverzögerte Zyklen tatsächlich in der Natur beobachtet worden sind, sind die Zyklen des Schneeschuhhasen (Lepus americanus) und seines Räubers, des Kanadischen Luchses (Lynx canadensis).[3] Die Arten zeigen über ein riesiges Gebiet (ein großer Teil des Nordens von Nordamerika, von Alaska bis Neufundland) einen Zyklus von etwa zehn Jahren Länge (tatsächlich beobachtet: 9–11 Jahre). Dieses Beispiel wurde sogar in Schulbücher übernommen. Ursprünglich als besonders schlagendes Beispiel für eine Oszillation vom Lotka-Volterra-Typ gedeutet, liegen nach neueren Untersuchungen die Verhältnisse hier viel verwickelter. Hohe Hasenpopulationen brechen anscheinend vor allem durch Nahrungsmangel zusammen. Knapp wird hier allerdings nicht Nahrung als solche (die Hasen fressen ihren Lebensraum nicht etwa kahl), sondern gute Nahrung mit hohem Nährwert. Die beweideten Pflanzen können bei starker Beweidung Fraßgifte (Toxine) bilden und werden dadurch für die Hasen weniger gut fressbar. Sie bilden diese (energetisch kostspieligen) Toxine aber nur, wenn hoher Fraßdruck besteht. Die Interaktion des „Prädatoren“ Schneeschuhhase und seiner pflanzlichen „Beute“ scheint hier den Zyklus anzutreiben. Der Luchs folgt demnach nur passiv nach. Dieses Beispiel (das keinesfalls bis in die letzten Einzelheiten aufgeklärt ist) zeigt anschaulich, dass man sich vor einfachen Erklärungen der komplexen Sachverhalte hüten sollte, auch wenn sie scheinbar gut in das zur Erklärung verwendete Modell passen.
Andere Modelle

Untersuchungen, die der US-amerikanische Zoologe und Ökologe Paul Errington (1946) für die Räuber-Beute-Beziehung zwischen Bisamratten und Minks durchgeführt hat, zeigen ein völlig anderes Verhalten. So ist der Mink zwar der wichtigste Räuber der Bisamratte, die Populationsgröße der Bisamratte wird jedoch weniger durch die Zahl ihrer Räuber beeinflusst als durch die Besatzdichte des Territoriums. Vor allem umherstreifende Tiere ohne Revier oder verletzte Tiere werden Beute des Mink. Es werden also die Individuen bevorzugt getötet, die ohnehin die geringste Überlebenswahrscheinlichkeit gehabt hätten. Die Populationsgröße der Beute wird in diesem Fall also durch den Ökofaktor Räuber auf eine regulierte Dichte begrenzt, die durch die Ökofaktoren Nahrung und Raum zum Anlegen von Bauen vorgegeben ist. Vergleichbare Fälle wurden bei anderen Untersuchungen sehr häufig gefunden.
Literatur
- Michael Begon, Martin Mortimer, David J. Thompson: Populationsökologie. Spektrum, Heidelberg/Berlin/Oxford 1997, ISBN 3-86025-258-5, S. 178–265.
Weblinks
- Hinweise zu Wator
- Java-Version einer Wator-Simulation
- Räuber-Beute-Simulation für Windows (Freeware)
- Die freie Multi-Agenten-Simulationsumgebung NetLogo enthält in ihrer mitgelieferte „Models Library“ ein „Schaf-Wolf-Gras“ Modell, welches das Populationswachstum eines Raubtier-Beute-Systems modelliert und visualisiert.[4]
Einzelnachweise
- Paws without claws? Large carnivores in anthropogenic landscapes
- Neil A. Campbell, Jane B. Reece: Biologie, 6. Auflage, Spektrum Akademischer Verlag, Heidelberg/ Berlin 2003, ISBN 3-8274-1352-4, S. 1388–1394.
- Nils Chr. Stenseth, Wilhelm Falck, Ottar N. Bjørnstad und Charles J. Krebs: Population regulation in snowshoe hare and Canadian lynx: Asymmetric food web configurations between hare and lynx. In: Proceedings of the National Academy of Sciences. Band 94, Nr. 10, 1997, S. 5147–5152
- Uri Wilensky: NetLogo Models Library: Wolf Sheep Predation. In: NetLogo Models Library. Abgerufen am 27. November 2018 (englisch).