SIR-Modell

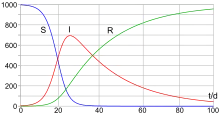
Als SIR-Modell (susceptible-infected-removed model) bezeichnet m​an in d​er mathematischen Epidemiologie, e​inem Teilgebiet d​er Theoretischen Biologie, e​inen klassischen Ansatz z​ur Beschreibung d​er Ausbreitung v​on ansteckenden Krankheiten m​it Immunitätsbildung, d​er eine Erweiterung d​es SI-Modells darstellt. Benannt i​st es n​ach der Gruppeneinteilung d​er Population i​n Suszeptible (S), d​as heißt Ansteckbare, Infizierte (I) u​nd aus d​em Infektionsgeschehen entfernte Personen (R), w​ie unten erläutert. Die Erweiterung d​es SIR-Modells u​nter Einbezug d​er Exponierten, a​lso Personen, d​ie infiziert, a​ber noch n​icht ansteckend sind, w​ird mit d​em SEIR-Modell beschrieben. Üblicherweise w​ird ein deterministisches, d​urch miteinander verknüpfte gewöhnliche Differentialgleichungen formuliertes Modell betrachtet, b​ei dem d​ie Variablen kontinuierlich s​ind und großen Gesamtheiten entsprechen. Es werden a​ber auch andere, insbesondere stochastische Modelle m​it SIR bezeichnet, d​ie mit d​em deterministischen SIR-Modell d​ie Gruppeneinteilung gemeinsam haben.

Zeitlicher Verlauf der drei Gruppen S, I und R mit den Startwerten ${\displaystyle S(0)=997}$, ${\displaystyle I(0)=3}$, ${\displaystyle R(0)=0}$ sowie Infektionsrate ${\displaystyle \beta =0{,}4}$ und Rate ${\displaystyle \gamma =0{,}04}$ für die Gruppe R. Die Raten sind in der Zeiteinheit Tag.

Stehen weder Medikamente noch eine Impfung zur Verfügung, so kann man nur die Zahl der Ansteckungen durch geeignete Maßnahmen reduzieren. Diese Animation zeigt, wie sich eine Senkung der Infektionsrate um 76 % (von ${\displaystyle \beta =0{,}5}$ auf ${\displaystyle \beta =0{,}12}$) auswirkt (die übrigen Parameter sind wie in der Grafik oben ${\displaystyle S(0)=997}$, ${\displaystyle I(0)=3}$, ${\displaystyle R(0)=0}$ und ${\displaystyle \gamma =0{,}04}$). Die Angaben zu ${\displaystyle \beta }$ sind dem Artikeltext angepasst, die Werte in der Abbildung entsprechen ${\displaystyle {\tfrac {\beta }{N}}}$ mit ${\displaystyle N=1000}$.

Das Modell stammt v​on William Ogilvy Kermack u​nd Anderson Gray McKendrick (1927)[1] u​nd wird a​uch manchmal n​ach beiden benannt (Kermack-McKendrick-Modell). Die Autoren konnten d​amit trotz d​er Einfachheit d​es Modells g​ut die Daten e​iner Pestepidemie i​n Bombay 1905/06 modellieren.

Differentialgleichungen

Beim SIR-Modell werden drei Gruppen von Individuen unterschieden: Zum Zeitpunkt ${\displaystyle t}$ bezeichnet ${\displaystyle S(t)}$ die Anzahl der gegen die Krankheit nicht immunen Gesunden (susceptible individuals), ${\displaystyle I(t)}$ die Zahl der ansteckenden Infizierten (infectious individuals) sowie ${\displaystyle R(t)}$ die Anzahl der aus dem Krankheitsgeschehen „entfernten“ Personen (removed individuals). Letzteres erfolgt entweder durch Genesen mit erworbener Immunität gegen die Krankheit oder durch Versterben.[2][3] In anderer Lesart sind es die resistenten Personen.[4] Weiterhin sei ${\displaystyle N}$ die Gesamtzahl der Individuen, das heißt:

${\displaystyle N=I+S+R\;.}$

Der einfacheren Schreibweise wegen wird die Zeitabhängigkeit bei ${\displaystyle N=N(t),R=R(t),S=S(t),I=I(t)}$ im Folgenden weggelassen. Es gilt für jede Zeit ${\displaystyle N(t)\geq 0}$, ${\displaystyle S(t)\geq 0}$, ${\displaystyle R(t)\geq 0}$, ${\displaystyle I(t)\geq 0}$.

Im SIR-Modell werden e​ine Reihe v​on Annahmen gemacht:

• Jedes Individuum kann von einem Erreger nur einmal infiziert werden und wird danach entweder immun oder stirbt.
• Infizierte sind sofort ansteckend, eine Annahme die im SEIR-Modell nicht getroffen wird.
• Die jeweiligen Raten sind konstant.
• Die durch die Infektion Verstorbenen werden wie die Immunisierten zu ${\displaystyle R}$ gerechnet.

Dann s​ind die Ratengleichungen d​es SIR-Modells:[4]

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=\nu \,N-\beta {\frac {S\,I}{N}}-\mu \,S\;,}$

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=\beta {\frac {S\,I}{N}}-\gamma \,I-\mu \,I\;,}$

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \,I-\mu \,R\;.}$

Mit d​en Raten:

${\displaystyle \gamma }$ Rate, mit der infizierte Personen in der Zeiteinheit genesen oder sterben (da die Toten auch zu ${\displaystyle R}$ gerechnet werden)

${\displaystyle \mu }$ allgemeine Sterberate pro Person einer Population (also „pro Kopf“)

${\displaystyle \nu }$ Geburtsrate pro Person einer Population (also „pro Kopf“)

${\displaystyle \beta }$, die Rate, die die Anzahl neuer Infektionen angibt, die ein erster infektiöser Fall pro Zeiteinheit verursacht. ${\displaystyle {\frac {\beta }{N}}}$ wird auch als Transmissionsrate oder Transmissionskoeffizient bezeichnet.[5]

${\displaystyle \beta }$ kann weiter aufgeschlüsselt werden: ${\displaystyle \beta =q\cdot \kappa }$, mit ${\displaystyle \kappa }$ der Kontaktrate und der Wahrscheinlichkeit ${\displaystyle q}$ einer Infektionsübertragung bei Kontakt.

Die Infektionsrate (englisch force of infection) ${\displaystyle \lambda }$, also die "pro Kopf" Rate mit der suszeptible Personen infiziert werden, ist

${\displaystyle \lambda =\beta {\frac {I}{N}}}$

wobei ${\displaystyle {\frac {I}{N}}}$ den Anteil infizierter Personen an der Gesamtbevölkerung und damit die Wahrscheinlichkeit des Kontakts mit einer infizierten Person darstellt. Es werden ${\displaystyle \lambda S}$ Personen pro Zeiteinheit infiziert.

Vernachlässigt man die Geburts- und Sterberaten ${\displaystyle \mu =\nu =0}$ (N ist dann konstant) ergeben sich die Gleichungen:

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=-\beta {\frac {S\,I}{N}}\;,}$

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=\beta {\frac {S\,I}{N}}-\gamma \,I\;,}$

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \,I\;.}$

Die Gleichungen s​ind ähnlich d​en Lotka-Volterra-Gleichungen i​n Räuber-Beute-Systemen u​nd gekoppelten Bilanzgleichungen a​uf vielen anderen Gebieten (Replikatorgleichungen).

In der Literatur wird zuweilen eine Variante der Gleichungen benutzt, in die der Transmissionskoeffizient ${\textstyle {\frac {\beta }{N}}}$ eingeht und dabei oft ebenfalls mit ${\textstyle \beta }$ bezeichnet wird, obwohl er einen anderen Wert hat: Ist etwa ${\textstyle N=1000}$ und unser Koeffizient oben ${\textstyle \beta =0{,}4}$, so muss in die Variante der Differentialgleichung der Wert ${\textstyle 0{,}0004}$ eingesetzt werden. Verwenden wir der Klarheit halber einen anderen Bezeichner ${\textstyle {\tilde {\beta }}}$, so schreibt sich die erste Differentialgleichung in der Variante:[Anm. 1]

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=-{\tilde {\beta }}S\,I\;.}$

Basisreproduktionszahl und Verlauf einer Epidemie

Die Basisreproduktionszahl ist

${\displaystyle R_{0}={\frac {\beta }{\gamma }}}$

Hierbei wird die übliche Bezeichnung für die Basisreproduktionszahl benutzt (sie ist nicht mit dem Anfangswert ${\displaystyle R(0)}$ der Anzahl resistenter Personen zum Zeitpunkt ${\displaystyle t=0}$ zu verwechseln, der zuweilen auch mit ${\displaystyle R_{0}}$ bezeichnet wird).

Die Basisreproduktionszahl ${\displaystyle R_{0}}$ gibt an, welche Anzahl an weiteren Infektionen eine infizierte Person (während der Gesamtdauer ihrer infektiösen Periode) in der Anfangszeit der Epidemie in einer komplett suszeptiblen Bevölkerung verursacht. Neben ${\displaystyle \beta }$ tritt hier noch der Faktor ${\displaystyle {\frac {1}{\gamma }}}$ auf, der die Dauer der infektiösen Periode angibt. In der Anfangszeit einer Epidemie kann man näherungsweise Geburts- und Sterberaten vernachlässigen, also ${\displaystyle \mu =\nu =0}$ setzen; dann erhält man die am Schluss des letzten Abschnitts angegebene Form der SIR-Gleichungen. Für den Beginn einer Epidemie muss ${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}>0}$ sein und folglich (da am Anfang ${\displaystyle N\approx S}$ gilt) gemäß den SIR-Gleichungen ${\displaystyle \beta >\gamma }$ und somit ${\displaystyle R_{0}={\frac {\beta }{\gamma }}>1}$ (siehe auch den folgenden Abschnitt über die diskretisierte Form der Gleichungen).

Im weiteren Verlauf wächst nach den SIR-Gleichungen die Zahl der Infizierten ${\displaystyle I}$, wenn ${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=I\,(\beta {\frac {S}{N}}-\gamma )>0}$, also ${\displaystyle \beta {\frac {S}{N}}>\gamma }$ und damit

${\displaystyle R_{0}{\frac {S}{N}}>1}$

Links steht das Produkt aus Basisreproduktionszahl und Anteil ${\displaystyle {\frac {S}{N}}}$ der Infizierbaren (Suszeptiblen) an der Population. Letzterer ist gleichzeitig die Wahrscheinlichkeit, bei einem Kontakt auf einen Infizierbaren zu treffen. Die Ungleichung ist gleichbedeutend mit[4]

${\displaystyle S>{\frac {N}{R_{0}}}}$

Das Wachstum der Infizierten nimmt ab (Abflauen bzw. Ende der Epidemie), falls ${\displaystyle S}$ den Wert ${\displaystyle \rho ={\frac {N}{R_{0}}}}$ unterschreitet. Bei einem Wert der Basisreproduktionszahl ${\displaystyle R_{0}=2}$ wäre das die Hälfte der Bevölkerung und bei ${\displaystyle R_{0}=3}$ ein Drittel, so dass im ersten Fall die Hälfte und in letzterem Fall zwei Drittel der Population infiziert oder resistent sind, d. h. nicht mehr empfänglich für eine Infektion sind; man spricht dann von „Herdenimmunität“.

Bei Influenza liegen beispielsweise d​ie Basisreproduktionszahlen üblicherweise zwischen 2 und 3.

Diskretisierte Form der Differentialgleichungen

Die diskretisierte Form der Differentialgleichungen mit Zeitschritt ${\displaystyle \Delta t}$ lautet:[6]

${\displaystyle S(t)-S(t-\Delta t)=-\beta \,\Delta t\,{\frac {S(t-\Delta t)}{N}}\,I(t-\Delta t):=-I_{\text{new}}(t)}$

${\displaystyle R(t)-R(t-\Delta t)=\gamma \,\Delta t\,I(t-\Delta t):=R_{\text{new}}(t)}$

${\displaystyle I(t)-I(t-\Delta t)=\left(\beta \,{\frac {S(t-\Delta t)}{N}}-\gamma \right)\,\Delta t\,I(t-\Delta t)=I_{\text{new}}(t)-R_{\text{new}}(t)}$

${\displaystyle I_{\text{new}}(t)}$ entspricht der Zahl neu Infizierter Personen im Beobachtungszeitraum ${\displaystyle \Delta t}$, also dem was auch in den offiziellen Statistiken als Zahl Neuinfizierter auftaucht,[6] wobei in der Praxis Korrekturen für Meldeverzug und anderes angebracht werden. Häufig wird ein Tag als Zeiteinheit und als Beobachtungszeitraum für die Meldung gewählt und ${\displaystyle \Delta t=1}$ gesetzt.

Für die Ableitung der Basisreproduktionszahl betrachte man die diskretisierte Form (Schritt ${\displaystyle \Delta t}$) der Differentialgleichung für ${\displaystyle I(t)}$:

${\displaystyle I(t)-I(t-\Delta t)=\left(\beta \,{\frac {S(t-\Delta t)}{N}}-\gamma \right)\,\Delta t\,I(t-\Delta t)}$

Mit der Dauer der infektiösen Periode ${\displaystyle D={\frac {1}{\gamma }}}$ eingesetzt für ${\displaystyle \Delta t}$ und nach Definition der Basisreproduktionszahl ${\displaystyle R_{0}}$ bzw. Nettoreproduktionszahl ${\displaystyle R}$:

${\displaystyle I(t)=R\,I(t-D)}$

wobei am Anfang der Epidemie ${\displaystyle R}$ als ${\displaystyle R_{0}}$ bezeichnet wird, ergibt sich

${\displaystyle I(t)-I(t-D)=\left(R-1\right)\,I(t-D)=\left(\beta \,{\frac {S(t-D)}{N}}-\gamma \right)\,D\,I(t-D)}$

Damit ist

${\displaystyle R={\frac {\beta }{\gamma }}\,{\frac {S}{N}}}$

und für ${\displaystyle R_{0}}$, da am Beginn der Epidemie ${\displaystyle S\approx N}$, ergibt sich:

${\displaystyle R_{0}={\frac {\beta }{\gamma }}}$

Mathematische Behandlung

Mit Hilfe des SIR-Modells können wir für gegebene Anfangswerte ${\displaystyle I_{0},S_{0},\beta ,\gamma }$ bestimmen, ob der Krankheitsverlauf in einer Epidemie münden wird. Diese Frage ist äquivalent zu der Frage, ob die Zahl der Infizierten zum Zeitpunkt ${\displaystyle 0}$ steigt. Betrachte die Ableitung:

${\displaystyle \left.{\frac {\mathrm {d} I}{\mathrm {d} t}}\right|_{t=0}=I_{0}\left({\frac {\beta S_{0}}{N}}-\gamma \right)>0\ \ {\text{für }}S_{0}>\rho$ :={\frac {\gamma }{\beta }}N} .

Hierbei nennen wir ${\displaystyle \rho }$ den Schwellenwert einer Epidemie, da aus ${\displaystyle S(t)\leq S_{0}}$ für alle Zeiten die Ungleichung ${\displaystyle {\dot {S}}\leq 0}$ für alle ${\displaystyle t\geq 0}$ folgt und für ${\displaystyle S_{0}<\rho }$ die Epidemie abflaut:

${\displaystyle {\dot {I}}(t)=I\left({\frac {\beta S}{N}}-\gamma \right)\leq 0}$.

für alle ${\displaystyle t\geq 0}$.

Eine Epidemie tritt im SIR-Modell also genau dann auf, wenn ${\displaystyle S_{0}>\rho }$ ist. Dies ist eine wesentliche Aussage des Modells, auch als Schwellwert-Theorem bekannt.[7] Um eine Epidemie zu starten, muss eine Mindestdichte von Infizierbaren vorhanden sein. Wird die Zahl der Infizierbaren im Lauf der Epidemie umgekehrt unter diese Schwelle gedrückt, erlischt die Epidemie.

Maximale Zahl der Infizierten

Aus den obigen Differentialgleichungen für ${\displaystyle I}$ und ${\displaystyle S}$ folgt:

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} S}}=-{\frac {(\beta S-\gamma N)I}{\beta SI}}=-1+{\frac {\rho }{S}}}$.

Integration d​urch Trennung d​er Variablen liefert:

${\displaystyle I(t)+S(t)-\rho \ln S(t)=I_{0}+S_{0}-\rho \ln S_{0}={\text{const.}}}$

mit ${\displaystyle \ln }$ der Logarithmusfunktion. Die Funktion ${\displaystyle I+S-\rho \ln S}$ ist ein erstes Integral des Systems und konstant auf den Trajektorien des Systems im durch ${\displaystyle I}$ und ${\displaystyle S}$ gegebenen Phasenraum. Die maximale Zahl der Infizierten ergibt sich offensichtlich für ${\displaystyle S_{0}\geq \rho }$ und bei ${\displaystyle S(t)=\rho }$. Mit der obigen Gleichung ergibt sich unter Annahme von ${\displaystyle R(0)=0}$:

${\displaystyle I_{\text{max}}=-\rho +\rho \ln(\rho )+I_{0}+S_{0}-\rho \ln S_{0}=N-\rho +\rho \ln \left({\frac {\rho }{S_{0}}}\right)}$

Setzt man ${\displaystyle S_{o}=N}$ und ${\displaystyle I_{0}=0}$ sowie ${\displaystyle \rho ={\frac {N}{R_{0}}}}$ erhält man:

${\displaystyle I_{\text{max}}={\frac {N}{R_{0}}}\left(R_{0}-1-\ln R_{0}\right)}$

Aus den ersten Integralen ergibt sich auch die Gleichung für ${\displaystyle S(\infty )}$ („final size equation“):

${\displaystyle \ln {\frac {S(\infty )}{N}}=R_{0}\cdot ({\frac {S(\infty )}{N}}-1)}$

aus den Werten für ${\displaystyle t=0}$ (mit ${\displaystyle S_{0}=N,I_{0}=0}$) und ${\displaystyle t=\infty }$ (mit ${\displaystyle I(\infty )=0}$). Die Gleichung kann zur Bestimmung von ${\displaystyle S(\infty )}$ benutzt werden. Insbesondere ergibt sich für ${\displaystyle R_{0}<1}$ die Lösung ${\displaystyle {\frac {S(\infty )}{N}}=1}$, das heißt, es gibt keinen Ausbruch.[8]

Zahl der „Überlebenden“

Es stellt sich auch die Frage, ob die Epidemie überhaupt „überlebt“ wird, das heißt, ob am Ende noch Suszeptible übrigbleiben. Dazu berechnen wir ${\displaystyle S(\infty )}$, also ${\displaystyle S(t)}$ mit der Zeit ${\displaystyle t}$ gegen Unendlich (${\displaystyle \infty }$). Analog ergibt sich aus den obigen Differentialgleichungen

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} R}}=-{\frac {S}{\rho }}}$, deren Lösung ${\displaystyle S=S_{0}\exp \left(-{\frac {R}{\rho }}\right)\geq S_{0}\exp \left(-{\frac {N}{\rho }}\right)>0}$ ist, mit der Exponentialfunktion ${\displaystyle \exp }$.

Damit folgt offensichtlich ${\displaystyle 0<S(\infty )<N}$, es wird also nicht die gesamte Population infiziert. Aus ${\displaystyle \lim _{t\to \infty }{\frac {\mathrm {d} S}{\mathrm {d} t}}=-{\frac {\beta }{N}}I(\infty )S(\infty )=0}$ folgt damit außerdem ${\displaystyle I(\infty )=0}$. Es zeigt sich, dass es am Ende einer Epidemie weniger an Suszeptiblen als eher an Infizierten mangelt!

Näherungen: Reduziere Zahl der Parameter

Das in den Lösungen des SIR-Modells vorkommende Quadrat des Sekans hyperbolicus (rot) hat eine noch steilere Flanke als der Sekans hyperbolicus selbst.

Wenn wir die Anfangswerte ${\displaystyle I_{0},S_{0},\beta ,\gamma }$ kennen, können wir mit den obigen Differentialgleichungen schnell die Dynamik einer Krankheit bestimmen. Oft lassen sich aber gerade diese Konstanten nur schwer bestimmen, weshalb wir im Folgenden die obigen Gleichungen nähern wollen.

Aus d​en besprochenen Differentialgleichungen f​olgt sofort[9]

$${\displaystyle {\begin{aligned}{\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma (N-R-S)=\gamma \left(N-R-S_{0}\exp \left(-{\frac {R}{\rho }}\right)\right).\end{aligned}}}$$

Die Gleichung vereinfacht sich zu einer riccatischen Differentialgleichung, wenn ${\displaystyle \exp \left(-{\frac {R}{\rho }}\right)}$ durch die ersten 3 Summanden der Taylorreihe um ${\displaystyle {\frac {R}{\rho }}=0}$ angenähert wird:

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \left(N-S_{0}\right)+\gamma \left({\frac {S_{0}}{\rho }}-1\right)R-\gamma {\frac {S_{0}}{2\rho ^{2}}}R^{2}=-\gamma {\frac {S_{0}}{2\rho ^{2}}}R^{2}+\gamma \left({\frac {S_{0}}{\rho }}-1\right)R+\gamma \left(N-S_{0}\right)}$

also

${\displaystyle R(t)={\frac {\rho ^{2}}{S_{0}}}\left(\left({\frac {S_{0}}{\rho }}-1\right)+\alpha \operatorname {tanh} \left({\frac {\alpha \gamma \,t}{2}}-\phi \right)\right)}$

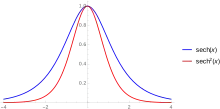
wobei eingeführt wurden:

${\displaystyle \alpha ={\sqrt {\left({\frac {S_{0}}{\rho }}-1\right)^{2}+2\,{\frac {S_{0}(N-S_{0})}{\rho ^{2}}}}}}$

${\displaystyle \phi =\tanh ^{-1}\left({\frac {1}{\alpha }}\left({\frac {S_{0}}{\rho }}-1\right)\right)}$

Die Funktion ${\displaystyle \operatorname {sech} }$ ist der Sekans hyperbolicus und ${\displaystyle \operatorname {tanh} }$ der Tangens hyperbolicus, ${\displaystyle \tanh ^{-1}}$ dessen Umkehrfunktion.

Damit lässt sich die Differentialgleichung für ${\displaystyle R}$ mit nur drei Parametern ausdrücken:

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}={\frac {\gamma \,\alpha ^{2}\rho ^{2}}{2S_{0}}}\operatorname {sech} ^{2}\left({\frac {\alpha \gamma \,t}{2}}-\phi \right)=B\cdot \operatorname {sech} ^{2}\left({\frac {A\cdot t}{2}}-\phi \right)}$

Diese drei Parameter sind also ${\displaystyle A=\alpha \gamma }$ (bei dem anfänglich exponentiellen Wachstum entspricht ${\displaystyle A={\frac {\ln 2}{t_{d}}}}$ mit ${\displaystyle t_{d}}$ der Verdopplungszeit), die Phase ${\displaystyle \phi }$ und ${\displaystyle B={\frac {\gamma \,\alpha ^{2}\rho ^{2}}{2S_{0}}}=\gamma \cdot I_{\text{max}}}$. Je nach Datenlage kann hierbei die Differentialgleichung oder die implizite Gleichung für ${\displaystyle R(t)}$ verwendet werden.

Setzt man ${\displaystyle I_{0}=0}$ und ${\displaystyle S_{0}>\rho }$ erhält man ${\displaystyle \alpha ={\frac {S_{0}}{\rho }}-1}$ und damit:

${\displaystyle R(t)={\frac {\rho ^{2}}{S_{0}}}\left({\frac {S_{0}}{\rho }}-1\right)\left(1+\operatorname {tanh} \left({\frac {\gamma }{2}}\left({\frac {S_{0}}{\rho }}-1\right)t-\phi \right)\right)}$

Mit ${\displaystyle \lim _{t\to \infty }\operatorname {tanh} \left(at+b\right)=1}$ erhält man einen Näherungswert für das „Ausmaß der Epidemie“ ${\displaystyle R(\infty )=S_{0}-S(\infty )}$:

${\displaystyle R(\infty )=S_{0}-S(\infty )=2\rho \left(1-{\frac {\rho }{S_{0}}}\right)}$

Damit erhält man den zweiten Teil des Schwellwerttheorems. Sei am Anfang ${\displaystyle S_{0}=\rho +v}$ mit ${\displaystyle v>0}$, dann ist das „Ausmaß der Epidemie“:

${\displaystyle R(\infty )=2\rho {\frac {v}{\rho +v}}\approx 2v}$

und ${\displaystyle S(\infty )=\rho -v}$. Die Anzahl suszeptibler Personen ist am Ende um ${\displaystyle 2v}$ gegenüber dem Stand vor der Epidemie reduziert.

Für d​ie Zahl d​er Infizierten ergibt s​ich gemäß d​er letzten Differentialgleichung i​m SIR-Modell:

${\displaystyle I(t)={\frac {1}{\gamma }}{\frac {\mathrm {d} R}{\mathrm {d} t}}={\frac {\alpha ^{2}\rho ^{2}}{2S_{0}}}\operatorname {sech} ^{2}\left({\frac {\alpha \gamma \,t}{2}}-\phi \right)}$

Der Verlauf von ${\displaystyle I(t)}$ hat die Form einer Glockenkurve mit anfangs exponentiellem Anstieg. Kermack und McKendrick fanden zum Beispiel für die Pestepidemie in Bombay 1905/06 (mit fast immer tödlichem Ausgang, so dass ${\displaystyle \gamma \approx 1}$, als Zeiteinheit für die Raten wurde eine Woche genommen) gute Übereinstimmung mit:[10]

${\displaystyle I(t)\approx {\frac {\mathrm {d} R}{\mathrm {d} t}}=890\cdot \operatorname {sech} ^{2}\left(0{,}2\cdot t-3{,}4\right)}$

Die g​ute Übereinstimmung machte d​ies zu e​inem häufig zitierten Beispiel i​n der mathematischen Epidemiologie, i​st aber a​uch kritisiert worden.[11]

David George Kendall fand 1956 exakte Lösungen für ${\displaystyle R(t)}$ und das SIR-Modell,[12] doch werden die Differentialgleichungen meist numerisch gelöst.

Erweiterung des Modells

Dieses SIRD-Modell stellt den zeitlichen Verlauf der vier Gruppen S, I, R und D dar für die Startwerte ${\displaystyle S(0)=997}$, ${\displaystyle I(0)=3}$, ${\displaystyle R(0)=0}$ sowie Infektionsrate ${\displaystyle \beta =0{,}4}$ (identisch mit Werten der Grafik für das SIR-Modell oben), einer Rate ${\displaystyle \gamma =0{,}035}$ für die Gruppe R sowie Mortalitätsrate ${\displaystyle \mu =0{,}005}$

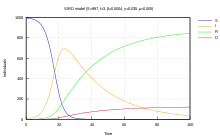
Will m​an die Toten separat betrachten (statt z​ur Gruppe R hinzuzurechnen), s​o kann m​an es z​um SIRD-Modell (Susceptible-Infected-Recovered-Deceased-Model) erweitern. Hierbei gehören z​ur Gruppe R n​ur die Individuen, welche d​ie Krankheit überlebt h​aben und i​mmun geworden sind, u​nd die Gestorbenen bilden e​ine eigene Gruppe D.[13]

Hierbei i​st folgendes System v​on Differentialgleichungen z​u lösen:[Anm. 2]

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=-\beta \cdot {\frac {S\cdot I}{N}}}$

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=\beta \cdot {\frac {S\cdot I}{N}}-\gamma \cdot I-\mu \cdot I}$

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \cdot I}$

${\displaystyle {\frac {\mathrm {d} D}{\mathrm {d} t}}=\mu \cdot I}$

Zum Zeitpunkt ${\textstyle t}$ gibt ${\textstyle R(t)}$ die Zahl der Genesenen und ${\textstyle D(t)}$ die Anzahl der an der Krankheit Verstorbenen an. Weiter bedeutet ${\textstyle \gamma }$ die Rate, mit der Infizierte gesunden, und ${\textstyle \mu }$ die Mortalitätsrate, mit der Infizierte versterben. ${\textstyle S(t)}$, ${\textstyle I(t)}$ sowie Transmissionsrate ${\textstyle {\frac {\beta }{N}}}$ haben dieselbe Bedeutung wie beim SIR-Modell.

Eine weitere Modifikation berücksichtigt die Impfung von Neugeborenen mit einem Anteil ${\displaystyle p}$:

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=\nu (1-p)\,N-\beta {\frac {S\,I}{N}}-\mu \,S}$

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=\beta {\frac {S\,I}{N}}-\gamma \,I-\mu \,I}$

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \,I+p\nu N-\mu \,R}$

Es g​ibt auch Varianten, i​n denen z​wei (oder mehr) Bevölkerungsgruppen betrachtet werden, z​um Beispiel d​ie Wechselwirkung e​iner Kerngruppe, d​ie besonders a​ktiv eine Infektion befördert, m​it der Restpopulation.[4]

Stochastische SIR-Modelle[4] dienen der Untersuchung kleinerer Populationen, die mit deterministischen Modellen nicht gut behandelt werden können. Dabei werden nur ganzzahlige Werte der Populationsanteile betrachtet und statistische Verteilungen für die Übergangsraten wie ${\displaystyle \beta }$. Der Verlauf von Epidemien ist hier nicht deterministisch vorbestimmt, d. h. eine Epidemie kann auch bei ${\displaystyle R_{0}>1}$ stoppen, wenn zufällig in der Infektionsperiode (infektiöse Periode, d. h. der Zeitspanne, in der ein Infizierter die Infektion übertragen kann) keine Kontakte stattfinden. Meist werden Simulationen (üblicherweise mit Monte-Carlo-Verfahren) mit den gleichen Parametern mehrfach durchgeführt und die Ergebnisse dann statistisch ausgewertet.

Eine Variante, d​ie Quarantänemaßnahmen u​nd Isolierungsmaßnahmen w​ie Soziale Distanzierung berücksichtigt, w​urde für d​ie Erklärung subexponentiellen Wachstums, d​as heißt Wachstum d​er Infizierten gemäß e​inem Potenzgesetz i​n der Zeit, b​ei Covid-19 i​n China a​b Ende Januar 2020 herangezogen (SIR-X-Modell).[14] Die Differentialgleichungen lauten i​n diesem Fall n​ach Dirk Brockmann u​nd Benjamin Maier (mit Anpassung a​n die h​ier gebrauchte Form d​er SIR-Gleichungen):

${\displaystyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=-\beta {\frac {S\,I}{N}}-\kappa _{0}S}$

${\displaystyle {\frac {\mathrm {d} I}{\mathrm {d} t}}=\beta {\frac {S\,I}{N}}-\gamma \,I-\kappa _{0}I-\kappa I}$

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \,I+\kappa _{0}S}$

${\displaystyle {\frac {\mathrm {d} X}{\mathrm {d} t}}=(\kappa +\kappa _{0})\,I}$

Dabei ist ${\displaystyle X}$ eine neu eingeführte Gruppe von symptomatischen infizierten Personen in Quarantäne und Isolation. Sie soll auch dem empirischen Vergleich mit den offiziell gemeldeten und bestätigten Fällen dienen. R sind die aus dem weiteren Infektionsgeschehen im Modell Entfernten (removed), entweder weil verstorben, genesen oder durch die allgemeinen Isolationsmaßnahmen, so weit sie nicht unter X fallen. Die allgemeinen Maßnahmen zur Kontaktreduzierung werden mit ${\displaystyle \kappa _{0}}$ beschrieben (soziale Distanzierung u. a.) und betreffen Infizierte und nicht Infizierte gleichermaßen, die speziellen Quarantänemaßnahmen für Infizierte mit dem Koeffizienten ${\displaystyle \kappa }$. Entfallen die jeweiligen Maßnahmen ist ${\displaystyle \kappa =\kappa _{0}=0}$. Es ergibt sich ein neues effektives ${\displaystyle R_{0,e}={\frac {\beta }{{\gamma }_{e}}}=\beta \cdot T_{i,e}}$ mit einer effektiven Infektionsperiode ${\displaystyle T_{i,e}={\frac {1}{{\gamma }_{e}}}={\frac {1}{\gamma +\kappa +\kappa _{0}}}}$. Dieses neue effektive ${\displaystyle R_{0,e}}$ ist kleiner als ${\displaystyle R_{0}}$. Eine andere Methode den Einfluss von isolierenden Maßnahmen zu simulieren besteht darin, für ${\displaystyle \beta }$ zeitlich variable Ansätze zu machen.[15]

Eine weitere Erweiterung besteht darin, n​icht die Gesamtzahl d​er Infizierten, sondern d​eren Dichte (Zahl d​er Infizierten p​ro Flächeneinheit) z​u berechnen, sodass a​uch die Verteilung d​er Infizierten i​m Raum betrachtet werden kann. Hierzu w​ird das gewöhnliche SIR-Modell u​m Diffusionsterme erweitert:

${\displaystyle {\begin{aligned}&\partial _{t}S=D_{S}\nabla ^{2}S-{\frac {\beta IS}{N}},\\[6pt]&\partial _{t}I=D_{I}\nabla ^{2}I+{\frac {\beta IS}{N}}-\gamma I,\\[6pt]&\partial _{t}R=D_{R}\nabla ^{2}R+\gamma I,\end{aligned}}}$

wobei ${\displaystyle D_{S}}$, ${\displaystyle D_{I}}$ und ${\displaystyle D_{R}}$ Diffusionskonstanten sind. Auf diese Weise erhält man eine Reaktions-Diffusions-Gleichung. (Damit die Einheiten korrekt sind, muss der Parameter ${\displaystyle \beta }$ modifiziert werden.) SIR-Modelle mit Diffusion wurden beispielsweise zur Beschreibung der Ausbreitung der Pest in Europa verwendet.[16] Erweiterte raumzeitliche SIR-Modelle ermöglichen die Beschreibung von kontaktreduzierenden Maßnahmen (social distancing).[17]

Ein v​on Matthias Kreck u​nd Erhard Scholz entwickeltes a​n Covid-19 adaptiertes Modell berücksichtigt Effekte v​on Impfungen, Massentests u​nd Mutanten. Das Modell w​urde speziell a​uf die Entwicklung i​n Deutschland angewendet. Ein vergleichsweise milder Eingriff, d​er die Zeit b​is zur Quarantäne u​m einen Tag reduziert k​ann zu e​iner drastischen Verbesserung führen, ebenso bestimmte Massentestungen. Das v​on Kreck u​nd Scholz angepasste SIR-Modell w​eist im Unterschied z​u dem Standard-SIR-Modell erhebliche Unterschiede auf, w​enn die Kontaktraten n​icht konstant sind. Die Modell-Reproduktionsrate weicht v​on der d​es RKI ab.[18]

Siehe auch

• Mathematische Modellierung der Epidemiologie (einführender Artikel)
• SI-Modell (Ansteckung ohne Gesundung)
• SIS-Modell (Ausbreitung von ansteckenden Krankheiten ohne Immunitätsbildung)
• SEIR-Modell (Ausbreitung von ansteckenden Krankheiten mit Immunitätsbildung, bei denen Infizierte nicht sofort infektiös sind)
• Dynamisches System (mathematischer Oberbegriff)

Literatur

• N. F. Britton: Essential Mathematical Biology. 1. Auflage. Springer, Berlin 2003, ISBN 1-85233-536-X.
• Michael Li: An introduction to mathematical modeling of infectious diseases, Springer, 2018

Weblinks

• Eric W. Weisstein: Kermack-McKendrick Model. In: MathWorld (englisch).
• Numberphile: The Coronavirus Curve auf YouTube, 25. März 2020, abgerufen am 16. Mai 2020.

Einzelnachweise

1. Kermack, McKendrick: A contribution to the mathematical theory of epidemics. Proc. Roy. Soc. A, Band 115, 1927, S. 700–721.
2. Sebastian Möhler: Ausbreitung von Infektionskrankheiten. (tu-freiberg.de [PDF; abgerufen am 12. März 2020]).
3. Regina Dolgoarshinnykh: Introduction to Epidemic Modelling. (columbia.edu [PDF; abgerufen am 12. März 2020]).
4. Eichner, Kretzschmar: Mathematische Modelle in der Infektionsepidemiologie. In: A. Krämer, R. Reintjes (Hrsg.): Infektionsepidemiologie. Springer, 2003, S. 81–94.
5. Michael Li: An introduction to mathematical modeling of infectious diseases. Springer, 2018, Abschnitt 2.1, Kermick-McKendrick-Model.
6. Viola Priesemann u.a.: Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science, 15. Mai 2020.
7. Norman Bailey: The mathematical theory of infectious diseases. Griffin and Company, 1975, S. 11, treshold theorem.
8. Odo Diekmann, Hans Heesterbeek, Tom Britton: Mathematical tools for understanding infectious disease dynamics. Princeton UP 2013, S. 15.
9. Die nachfolgende Ableitung mit den zugehörigen Formeln findet sich z. B. in Michael Li: An introduction to mathematical modeling of infectious diseases. Springer, 2018, S. 45.
10. Kermack, McKendrick: A contribution to the mathematical theory of epidemics. Proc. Royal Soc. A, Band 115, 1927, S. 714.
11. Nicholas Bacaer: The model of Kermack and McKendrick for the plague epidemic in Bombay and the type reproduction number with seasonality. Journal of Mathematical Biology, Band 64, 2012, S. 403–422. Danach sind die erhaltenen konstanten Parameter unrealistisch und die Pestepidemie trat 1897 bis mindestens 1911 saisonal in Bombay auf, gekoppelt an die Rattenpopulation, so dass ein komplexeres Modell nötig ist.
12. D. G. Kendall: Deterministic and stochastic epidemics in closed populations. Proc. Third Berkeley Symposium Math. Stat. & Prob., Band 4, 1956, University of California Press, S. 149–165 (Project Euclid).
13. Amenaghawon Osemwinyen, Aboubakary Diakhaby: Mathematical Modelling of the Transmission Dynamics of Ebola Virus. Juli 2015 (researchgate.net [abgerufen am 12. März 2020]).
14. Benjamin Maier, Dirk Brockmann: Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science, 8. April 2020 (Online).
15. Zum Beispiel Q. Lin u.a.: A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infectious Diseases, Band 93, 2020, S. 211–216.
16. J.V. Noble: Geographic and temporal development of plagues. In: Nature. 250, 1974, S. 726–729. doi:10.1038/250726a0.
17. Michael te Vrugt, Jens Bickmann, Raphael Wittkowski: Effects of social distancing and isolation on epidemic spreading modeled via dynamical density functional theory. In: Nature Communications. 11, 2020, S. 5576. doi:10.1038/s41467-020-19024-0.
18. Matthias Kreck, Erhard Scholz: Back to the roots: A discrete Kermack-McKendrick model adapted to Covid-19. 1. April 2021 (cornell.edu [abgerufen am 10. Juli 2021]).

Anmerkungen

1. Diese Form (in der ${\textstyle N}$ nicht vorkommt) benutzen Kermack und McKendrick für ihr SIR-Modell. Auf S. 713 benutzen sie die Funktionen ${\textstyle x(t),y(t),z(t)}$ für ${\textstyle S(t),I(t),R(t)}$ sowie ${\textstyle \kappa ,l}$ für Infektionsrate bzw. die Rate für die Gruppe R und schreiben

   ${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=-\kappa xy\;,}$

   ${\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} t}}=\kappa xy-ly\;,}$

   ${\displaystyle {\frac {\mathrm {d} z}{\mathrm {d} t}}=ly\;.}$

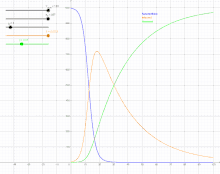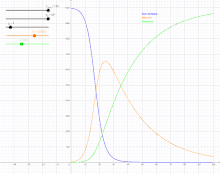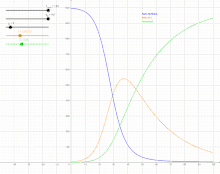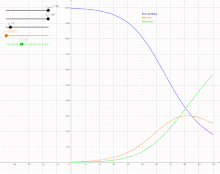
2. Die in der Quelle angegebenen Differentialgleichungen sind hierbei der Vergleichbarkeit halber in dieselbe Form gebracht worden wie beim SIR-Modell oben. Es gibt in der Literatur keine einheitliche Verwendung der Parameter; neben der obigen DGL ${\textstyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=-\beta {\frac {S(t)\cdot I(t)}{N}}}$ ist z. B. auch ${\textstyle {\frac {\mathrm {d} S}{\mathrm {d} t}}=-{\tilde {\beta }}\cdot S(t)\cdot I(t)}$ (Infektionsrate der Klarheit halber hier ${\textstyle {\tilde {\beta }}}$ benannt) üblich. Es gilt dann die Identität ${\textstyle {\tilde {\beta }}={\frac {\beta }{N}}}$. Bei den oben verwendeten Abbildungen ist ${\textstyle N=1000}$, und die Beschreibungen auf Wikimedia Commons beziehen sich auf die letztgenannte Variante der DGL, sodass die dort genannten Infektionsraten nur ${\textstyle {\frac {1}{1000}}}$ der Werte laut Nomenklatur im Artikel betragen (die Bildunterschriften wurden für den Artikel angepasst).