Photogrammetrie

Photogrammetrie oder Fotogrammetrie, auch Bildmessung genannt, ist eine Gruppe von berührungslosen Messmethoden und Auswerteverfahren, um aus Fotografien eines Objektes durch Bildmessung seine Lage und Form indirekt zu bestimmen sowie durch Bildinterpretation dessen Inhalt zu beschreiben. Neben Fotografien kommen aber auch andere Sensoren zum Einsatz wie Radar mit synthetischer Apertur (SAR) und Laserscanner. Im Gegensatz zu anderen Fachgebieten wie Fernerkundung, Kartografie oder Computer Vision, die ebenfalls mit berührungslosen Sensoren arbeiten, steht bei der Photogrammetrie die exakte dreidimensionale geometrische Rekonstruktion des aufgenommenen Objekts im Vordergrund. Im Regelfall werden dafür die Bilder mit speziellen Messkameras aufgenommen. Das Ergebnis wird meist als digitales Modell (Digitales Geländemodell) und in Form von Bildern, Plänen und Karten dargestellt.[1]

Geschichte

Die Theorie der Photogrammetrie wurde Mitte des 19. Jahrhunderts in Frankreich und Preußen parallel zur aufkommenden Fotografie entwickelt. Der französische Offizier Aimé Laussedat veröffentlichte 1851 seine Schrift Métrophotographie, der deutsche Architekt Albrecht Meydenbauer publizierte 1858 sein photogrammetrisches Verfahren zur Gebäudevermessung. Er gab der Photogrammetrie ihren Namen und gründete 1885 die erste photogrammetrisch arbeitende Behörde der Welt, die Königlich Preussische Messbild-Anstalt. Auch Édouard Gaston Deville und Paul Gast waren einige der Pioniere dieser Methode. 1907 erfand Eduard von Orel den Stereoautografen, der ab 1909 von der Firma Carl Zeiss kommerziell hergestellt wurde. Mit diesem Gerät konnten erstmals die Höhenschichtlinien automatisch durch optisches Abtasten der Fotos (Stereo-Bildpaare) gezeichnet werden.[2]

1930 stellte Gast die Bündelblockausgleichung in seinem Werk Vorlesung über Photogrammetrie vor, die auf der von Carl Friedrich Gauß erdachten Ausgleichsrechnung basiert. Sie wird seit den 1960er Jahren in großem Stil auf Computern eingesetzt. Als am Ende der 1980er Jahre großformatige Fotoscanner für Luftbilder bzw. Videokameras und Digitalkameras für Nahbereichs-Aufnahmen verfügbar waren, wurden die analogen Methoden der Photogrammetrie in den meisten Anwendungen durch digitale Auswerteverfahren ersetzt. Im ersten Jahrzehnt des 21. Jahrhunderts vollzog sich der letzte Schritt zur Volldigitalisierung, indem auch in der Luftbildphotogrammetrie die herkömmlichen filmbasierten Kameras zunehmend von digitalen Sensoren abgelöst wurden.

In den letzten Jahren hat die Bedeutung der Luftbildphotogrammetrie auch für eher kleinräumige Anwendungen zugenommen, da leistungsfähige Kameradrohnen immer erschwinglicher werden und durch ihre kompakten Abmessungen und Steuerungsmöglichkeiten auch sinnvoll in Flughöhen und an Orten eingesetzt werden können, wo der Einsatz manntragender Fluggeräte nicht möglich oder nicht praktikabel ist.

Ursprung des Begriffs

Eine Aufnahme des Wetzlarer Doms um das Jahr 1900 von Albrecht Meydenbauer. Auf der Aufnahme hat er mit einem Pfeil und der Beschriftung „September ’58“ die Stelle markiert, an der er 1858 verunglückte. Der Unfall motivierte ihn zur Entwicklung der Photogrammetrie. Auf der Rückseite des Fotos steht „Wetzlar 1858 – Die Gefahr des Absturzes mit (Pfeil) bezeichnet. Veranlassung zur Erfindung der Meßbildkunst.“

Albrecht Meydenbauer bezeichnete das Verfahren zunächst 1867 als „Photometrographie“.[3] Der Name „Photogrammetrie“ wurde erstmals am 6. Dezember 1867 als Titel des anonym veröffentlichten Beitrages Die Photogrammetrie im Wochenblatt des Architektenvereins zu Berlin (später Deutsche Bauzeitung) verwendet.[4] Die Redaktion des Wochenblatts bemerkt hierzu: „Der Name Photogrammetrie ist entschieden besser gewählt als Photometrographie, obgleich auch noch nicht ganz bezeichnend und zufriedenstellend.“[5] Da Wilhelm Jordan für sich in Anspruch nahm, den Namen Photogrammetrie 1876 eingeführt zu haben,[6] teilte die Redaktion der Deutschen Bauzeitung am 22. Juni 1892 unter Vermischtes mit, dass der 1867 veröffentlichte Beitrag von Albrecht Meydenbauer stammte.[7]

Überblick

Aufgaben

Aufgaben und Methoden des Faches – das meist an Technischen Universitäten im Rahmen der Geodäsie gelehrt wird – sind nach Meyers Lexikon[8] wie folgt:

Aufnahme und Auswertung ursprünglich nur fotografischer Messbilder zur Bestimmung von Beschaffenheit, Form und Lage beliebiger Objekte. Die Photogrammetrie erfährt heute eine bedeutende Ausweitung dank neuartiger Bildaufnahmegeräte und der digitalen Bildverarbeitung als Folge der Möglichkeiten von Optoelektronik, Computertechnik und digitalen Massenspeichern. Hauptanwendungsgebiet der Photogrammetrie ist die →Geodäsie.

Dazu kommen heute unter anderem die Herstellung von Landkarten, von digitalen GIS-Landschaftsmodellen und Spezialaufgaben wie etwa die Architekturphotogrammetrie und Unfallphotogrammetrie sowie in medizinischen Anwendungen (z. B. Virtopsy).

Einteilungen

Die Photogrammetrie lässt sich auf unterschiedliche Art und Weise einteilen. Nach Aufnahmeort und Entfernung unterscheidet man zwischen Luftbild- und Satellitenphotogrammetrie, terrestrischer Photogrammetrie und Nahbereichsphotogrammetrie. Die terrestrische Photogrammetrie (Erdbildmessung), bei der die Messbilder von erdfesten Standpunkten aus aufgenommen werden (Foto theodolit), wird im geodätischen Bereich zum Beispiel bei topografischen Aufnahmen im Hochgebirge und bei Ingenieurvermessungen genutzt. Dabei sind die Aufnahmeentfernungen in der Regel kleiner als 300 m und werden dann als Nahbereichsphotogrammetrie bezeichnet. Bei der Aerophotogrammetrie (Luftbildmessung) werden die Messbilder vorwiegend zur Herstellung topografischer Karten, für Katastermessungen und zur Gewinnung eines Höhenmodells mit einer →Messkammer vom Flugzeug (oder Satellit) aus aufgenommen (→Luftbildfotografie). Bei der Verwendung von Radar anstatt Licht spricht man auch von Radargrammetrie.

Nach der Anzahl der verwendeten Bilder werden die Verfahren der Einbild-, Zweibildphotogrammetrie (Stereophotogrammetrie) und Mehrbildmessung unterschieden. Die Messbilder werden in Einzelbildauswertegeräten entzerrt oder an stereoskopischen Doppelbild-Auswertegeräten in drei Dimensionen ausgemessen.

Nach Aufnahme- und Auswertemethode unterscheidet man Messtischphotogrammetrie grafisch-zeichnerische Auswertung (bis ca. 1930), Analogphotogrammetrie zur Auswertung analoger Bilder mittels optisch-mechanischer Geräte (bis ca. 1980), analytische Photogrammetrie zur rechnergestützten Auswertung analoger Bilder (bis ca. 2000) und die digitale Photogrammetrie zur Auswertung digitaler Bilder am PC (seit ca. 1985).

Je nach Anwendungsgebiet unterteilt man in Architekturphotogrammetrie zur Vermessung von Architektur und Kunstwerken, Ingenieurphotogrammetrie für allgemeine ingenieurtechnische Anwendungen. Darüber hinaus gibt es auch nicht-geodätischen Anwendungen wie zur Unfall- und Tatortvermessung, biomedizinische Anwendungen, die Land- und Forstwirtschaft, die Röntgenologie sowie Ingenieurbau und technisches Versuchswesen.[9]

Prinzipielle Methoden

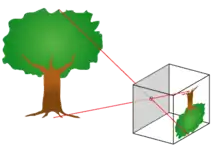
Zentralprojektion als Abbildungsmodell der Lochkamera. Ein Objekt wird durch das Loch auf dem Kopf stehend und seitenverkehrt abgebildet.

Der photogrammetrische Prozess beginnt mit der Aufnahme eines Objekts. Dabei wird ein Objekt entweder mit einem passiven Sensor (wie eine Kamera) aufgenommen oder einem aktiven Sensor (Laserscanner) gescannt. In jedem Fall entsteht die Aufnahme durch einen komplexen physikalischen Prozess. Im Fall eines passiven Sensors wird in der Regel das Sonnenlicht von der Erdoberfläche reflektiert und teilweise absorbiert, durchläuft dabei die Atmosphäre, bis sie durch das Objektiv einer Kamera auf den lichtempfindlichen Sensor trifft. Die Bildaufnahme unterliegt also einer Vielzahl an Einflüssen, angefangen bei der elektro-magnetischen Strahlung als Überträger der Information, der Wechselwirkung mit dem Oberflächenmaterial, den atmosphärischen Bedingungen und schließlich dem Objektiv und dem Sensor der Kamera. Dabei kommt es insbesondere zu geometrischen und radiometrischen (farblichen) Veränderungen der Bildaufnahme. Es sind daher Methoden notwendig, welche diese physikalischen Gegebenheiten angemessen berücksichtigen.

Bei der photogrammetrischen Auswertung von Bildern muss die Abbildungsgeometrie zum Zeitpunkt der Aufnahme wiederhergestellt werden. Diese Wiederherstellung erfolgt nach den Gesetzen der Zentralprojektion unter Einhaltung der Komplanaritätsbedingung. Dabei legt jedes Bild für einen abgebildeten Punkt $P'$ zusammen mit dem Projektionszentrum $O$ der jeweiligen Kamera eine Richtung zum Objektpunkt $P$ fest. Kennt man die Lage (Position und Ausrichtung) der Kamera (äußere Orientierung) sowie die Abbildungsgeometrie innerhalb der Kamera (innere Orientierung) dann kann jeder Strahl im Raum beschrieben werden.

Durch Verwendung von mindestens zwei homologen (korrespondierenden) Bildpunkten zweier verschiedener Aufnahmepositionen (Stereo-Bildpaar) kann man bei Kenntnis der gegenseitigen Lage (relative Orientierung) die beiden Strahlen zum Schnitt bringen und so jeden Objektpunkt dreidimensional berechnen. Dabei kommen in der Regel Verfahren der Ausgleichungsrechnung zum Einsatz (Bündelausgleichung). Aus verfahrenstechnischer Sicht war es früher (und zum Teil heute noch) notwendig die 3D-Rekonstruktion zunächst in einem temporären Modellkoordinatensystem durchzuführen. In diesem Fall musste man anschließend eine Transformation ins gewünschte Zielsystem durchführen (absolute Orientierung).

Innere Orientierung

Die innere Orientierung einer Kamera beschreibt die Lage des Projektionszentrums $O$ bezüglich der Bildebene. Dies sind die Koordinaten ( $x_{H},y_{H}$ ) des Bildhauptpunktes $H$ und der lotrechte Abstand $c$ (Kamerakonstante) zwischen der Bildebene und dem Projektionszentrum ( $c={\overline {OH}}$ ). Diese drei Elemente sind wesentliche Parameter des Lochkameramodells und beschreiben deren innere Geometrie. Da eine reale Kamera von diesem idealisierten Modell der Lochkamera abweicht, benötigt man weitere Parameter, welche diese Abweichungen beschreiben. Diese Abweichungen werden unter dem Begriff Verzeichnung zusammengefasst. Erst nachdem man die Verzeichnung korrigiert hat, stimmen die Bildpositionen mit den ursprünglichen Abbildungsstrahlen wieder überein. Deswegen zählt man die Verzeichnung meist zu den Daten der inneren Orientierung. Mittels einer Kamerakalibrierung lassen sich die Parameter der inneren Orientierung bestimmen.

Äußere Orientierung

Die äußere Orientierung beschreibt die räumliche Bildlage während der Aufnahme insbesondere die Position des Projektionszentrums und die Blickrichtung der Kamera. Damit stellt man den Bezug der Kamera zu einem übergeordneten globalen Koordinatensystem her. Dies geschieht mit Hilfe von Passpunkten, auf die man die entsprechenden Bildkoordinaten im Zuge eines räumlichen Rückwärtsschnittes iterativ einrechnet.

Kollinearitätsgleichungen

Bei bekannter innerer und äußerer Orientierung lässt sich der funktionale Zusammenhang zwischen den 3D-Koordinaten der Objektpunkte und deren abgebildeten Bildkoordinaten herstellen. Das zugrunde liegende Modell ist die Lochkamera, welche die technische Umsetzung der Zentralprojektion darstellt. Die mathematische Formulierung der Zentralprojektion ergeben die Kollinearitätsgleichungen, die gleichzeitig die zentralen Gleichungen der Photogrammetrie darstellen:

$x=x_{H}-s_{x}\cdot c\cdot {\frac {r_{11}\cdot (X-X_{0})+r_{12}\cdot (Y-Y_{0})+r_{13}\cdot (Z-Z_{0})}{r_{31}\cdot (X-X_{0})+r_{32}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}+\Delta {x}$

$y=y_{H}-s_{y}\cdot c\cdot {\frac {r_{21}\cdot (X-X_{0})+r_{22}\cdot (Y-Y_{0})+r_{23}\cdot (Z-Z_{0})}{r_{31}\cdot (X-X_{0})+r_{32}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}+\Delta {y}$

Die Bedeutungen der Symbole sind im Folgenden erklärt:

$c$ – Kammerkonstante
$r_{ij}$ – Parameter der 3×3-Rotationsmatrix (vom globalen zum Kamerakoordinatensystem)
$s_{x},s_{y}$ – Faktoren zur unterschiedlichen Skalierung von Sensorpixeln (nur bei nicht quadratischen Sensorelementen nötig)
$X_{0},Y_{0},Z_{0}$ – Koordinaten des Projektionszentrums (bezüglich des globalen Koordinatensystems)
$X,Y,Z$ – 3D-Koordinaten eines Objektpunkts (bezüglich des globalen Koordinatensystems)
$x_{H},y_{H}$ – Koordinaten des Bildhauptpunkts $H$ (bezüglich des Rahmenmarkensystems bei analogen Bildern (Film) oder bezüglich des Sensorsystems). Hinweis: je nachdem, welche Ausrichtung man bei den Achsen des Sensorsystems wählt, muss der Bruch für $y$ mit −1 multipliziert werden, weil die Achse des SKS entgegengesetzt gerichtet ist gegenüber dem Bildkoordinatensystem (s. Kollinearitätsgleichung#Stufe 3 – Zusammenfassung der Transformation Variante 3).
$\Delta x$ und $\Delta y$ – Funktionen zur Spezifizierung der Verzeichnungskorrekturen

Alternativ lässt sich der funktionale Zusammenhang der Zentralprojektion unter Verwendung von homogenen Koordinaten mit Hilfe von projektiver Geometrie auch linear formulieren (s. Projektionsmatrix). Sie ist äquivalent zur klassischen Kollinearitätsgleichung. Diese Formulierung ist jedoch aus dem Fachgebiet Computer Vision entstanden und nicht in der Photogrammetrie. Der Vollständigkeit halber soll es aber erwähnt werden.

Relative Orientierung

Wiederherstellung der relativen Lage zweier Bilder im Raum zueinander und Berechnung eines sogenannten Modells. Aus den Koordinaten der beiden Bilder $P_{1}(x,y,c)$ und $P_{2}(x,y,c)$ werden die Modellkoordinaten $P_{12}(u,v,w)$ berechnet. In der Praxis lassen sich so zahlreiche Bilder, zum Beispiel aus Luftaufnahmen, zu einem Modellverbund zusammenrechnen

Absolute Orientierung

Der Modellverbund aus der relativen Orientierung entspricht bereits der Geometrie der Punkte in der Örtlichkeit, allerdings stimmt die räumliche Orientierung des Modellverbundes noch nicht mit der Örtlichkeit überein und der Maßstab ist noch unbekannt. Im Zuge einer dreidimensionalen Helmert-Transformation werden die Modellkoordinaten des Modellverbundes auf die bekannten Passpunkte in der Örtlichkeit transformiert. Die Helmerttransformation passt die Punkte so in das bestehende Punktfeld ein, dass die Restklaffungen in den Koordinaten minimal werden. Bei Verwendung einer Restfehlerinterpolation lassen sich auch diese Klaffungen beseitigen.

Früher erfolgte die Auswertung zweier Luftbilder in Luftbildauswertegeräten, die die relative und absolute Orientierung durch physische Wiederherstellung der Strahlenbündel erreichte. Heute erfolgt die Auswertung in der Regel in Komparatoren, in denen Bildkoordinaten direkt gemessen werden. Die weiteren Arbeitsschritte sind dann Verfahrensgänge der numerischen Photogrammetrie, wobei Modellblock- und Bündelblockausgleichungsverfahren zum Einsatz kommen.

Kamerakalibrierung

Bei der Kamerakalibrierung werden die Abbildungseigenschaften, also die innere Orientierung, der Kamera und die äußere Orientierung aus den bekannten Bild- und 3D-Koordinaten der Objektpunkte berechnet.

Bildmessung

Die Bildmessung bestimmt die exakten Bildkoordinaten der Abbildung eines Objektpunktes in einem Bild. Im einfachsten Fall erfolgt die Bildmessung manuell. Auf einem Negativ oder Positiv wird die Position des interessierenden Objektpunktes von einem Menschen mit einer Messvorrichtung bestimmt. Da diese Methode sehr fehleranfällig und langsam ist, verwendet man heute fast ausnahmslos computergestützte Verfahren zum Suchen und Vermessen von Objekten in Bildern. Dabei kommen Methoden der digitalen Bildverarbeitung und der Mustererkennung zum Einsatz. Man kann diese Aufgaben durch die Verwendung von künstlichen Signalmarken wesentlich vereinfachen. Diese können mit automatischen Methoden identifiziert und sehr präzise auf 1/50 bis 1/100 Pixel im Bild lokalisiert werden.

Rückwärtsschnitt

Der Rückwärtsschnitt berechnet die Kameraposition, also die äußere Orientierung aus der bekannten inneren Orientierung, den 3D-Koordinaten der Objektpunkte und ihren Bildkoordinaten. In der klassischen Geodäsie sind dafür mindestens drei Festpunkte erforderlich, während man bei Messbildern zur Genauigkeitssteigerung meist eine größere Zahl von Punkten heranzieht. (Anmerkung: im Normalfall sind 6 Passpunkte zur Orientierung eines Messbildes erforderlich).

Vorwärtsschnitt

Mit einem Vorwärtsschnitt kann man bei mindestens zwei bekannten äußeren und inneren Orientierungen und den dazugehörigen Bildkoordinaten die 3D-Koordinaten der Objektpunkte berechnen. Voraussetzung ist, dass mindestens zwei Fotografien eines Objektes aus unterschiedlichen Richtungen aufgenommen wurden, ob gleichzeitig mit mehreren Kameras oder sequentiell mit einer Kamera spielt dabei für das Prinzip keine Rolle.

Modellblockausgleich

Zwei Bilder in einem analogen oder analytischen Auswertegerät sind relativ zu orientieren. Die entstehenden räumlichen Modellkoordinaten werden mit Hilfe verketteter dreidimensionaler Helmert-Transformationen in einer gemeinsamen Ausgleichung auf die Erdoberfläche transformiert (absolute Orientierung). Die Numerik der zu lösenden Gleichungen besteht lediglich aus Rotationen, Translationen und einem Maßstab. Durch Bezug der Koordinaten auf ihren Schwerpunkt zerfallen die Normalgleichungen des Ausgleichungssystems und die zur Ausgleichung eines Modells notwendigen 7 Unbekannten reduzieren sich auf zwei Normalgleichungen mit 4 und 3 Unbekannten. Da die Numerik nicht allzu anspruchsvoll ist, fand dieses Berechnungsverfahren weite Verbreitung.

Ein Ende der 70er Jahre an der Universität Stuttgart entwickeltes Programmsystem führte die Bezeichnung PAT-M43 (Programmsystem Aerotriangulation – Modellblockausgleichung mit 4 bzw. 3 Unbekannten). Die erreichbaren Genauigkeiten bei Modellblockausgleichungen ergeben mittlere Fehler für die Lage von ±7 µm und für die Höhe von ±10 µm. Ähnliche Programmsysteme entstanden mit dem Orient der TU Wien und auf anderen Hochschulen.

Bündelblockausgleich

Die Bündelblockausgleichung ist das wichtigste Verfahren der Photogrammetrie. Mit ihm kann man aus groben Näherungswerten für äußere und innere Orientierung gleichzeitig alle unbekannten Größen der Kollinearitätsgleichungen berechnen. Als bekannte Größe benötigt man lediglich die Bildkoordinaten der Objektpunkte, sowie zusätzliche Beobachtungen in Form eines Längenmaßstabes oder die räumlichen Koordinaten von Passpunkten. Diese Methode ist das am häufigsten eingesetzte Verfahren der Photogrammetrie bei statischen Messobjekten. Der Hauptvorteil liegt vor allem in der Möglichkeit einer Simultankalibrierung. Das heißt, dass die Messkamera während der eigentlichen Messung kalibriert wird. Mess- und Kalibrieraufnahmen sind also identisch, was den Aufwand für die Messung reduziert und gleichzeitig garantiert, dass die Messkamera stets kalibriert ist. Allerdings eignen sich nicht alle Konfigurationen von Objektpunkten für eine Simultankalibrierung. Dann müssen entweder zusätzliche Objektpunkte in die Messung miteinbezogen werden oder separate Kalibrieraufnahmen gemacht werden.

Der Bündelblockausgleich basiert, wie der Name sagt, auf der gemeinsamen Berechnung von Bündelblöcken. Von der theoretischen Seite her ist es im Vergleich mit dem Modellblockausgleich das strengere Verfahren. Die Beschaffung der Ausgangsdaten ist allerdings einfacher. Die weitere Berechnung über die Modellbildung bis zur absoluten Orientierung erfolgt in einer einzigen Ausgleichungsrechnung. Die Anforderungen an die Numerik sind allerdings wesentlich höher als beim Modellblockausgleich: die Normalgleichungen zerfallen nicht und die Anzahl der Unbekannten ist mit bis zu mehreren Tausend deutlich höher.

Weitere Verfahren

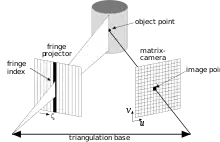
Prinzip des Streifenprojektionsverfahrens

Strukturiertes Licht bzw. Streifenprojektion

Ein weiteres Verfahren ist das „Streifenlichtscanning“ (englisch: „Structured Light Scanning“). Hierbei wird mit einem Projektor strukturiertes Licht auf das zu messende Objekt projiziert und von einer Kamera aufgenommen. Wenn man die gegenseitige Lage des Projektors und der Kamera kennt, kann man die abgebildeten Punkte entlang eines Streifens mit der bekannten Ausrichtung des Streifens vom Projektor zum Schnitt bringen. Es gibt verschiedene Varianten, die mit unterschiedlich projiziertem Licht arbeiten (s. auch Streifenprojektion und Lichtschnittverfahren).

Laserscanning

Unter Laserscanning (s. auch terrestrisches Laserscanning) umfasst man verschiedene Methoden, bei der ein Laser die Oberfläche zeilenförmig "abtastet". Dabei wird für jede einzelne Position die Entfernung zum Objekt über eine Laufzeitmessung bestimmt. Nach dem gleichen Prinzip funktioniert auch das Lidar (englische Abkürzung für light detection and ranging).

3D-TOF-Kameras

Hinter der Abkürzung 3D-TOF verbirgt sich die englische Bezeichnung 3D-time-of-flight, was man sinngemäß als dreidimensionale Laufzeit übersetzen kann. Es liegt also ebenfalls eine Laufzeitmessung des Lichtes zugrunde. Der Unterschied zu anderen Verfahren wie Laserscanning oder Lidar ist, dass es ein flächenhafter Sensor ist. Ähnlich wie bei einer normalen Digitalkamera enthält die Bildebene gleichmäßig angeordnete Lichtsensoren und zusätzlich winzige LEDs (oder Laserdioden), die einen infraroten Lichtpuls aussenden. Das von der Oberfläche reflektierte Licht wird von der Optik eingefangen und auf den Sensor abgebildet. Ein Filter sorgt dafür, dass nur die ausgestrahlte Farbe durchgelassen wird. Dies ermöglicht die gleichzeitige Entfernungsbestimmung eines Oberflächenstücks.

Anwendungen

Luftbildphotogrammetrie

Bei der Luftbildphotogrammetrie werden die Fotografien mit flugzeuggetragenen, digitalen oder analogen Messbildkameras aufgenommen. Es entstehen meist regelmäßige, streifenweise angeordnete Bildverbände, in denen sich benachbarte Bilder deutlich überlappen. Die Bildverbände werden orientiert, also in ein gemeinsames Koordinatensystem transformiert. Die Orientierung der Bildverbände erfolgt anhand von Pass- und Verknüpfungspunkten im Rahmen einer Bündelblockausgleichung. Aus den orientierten Bildern können Folgeprodukte wie 3D-Punkte, digitale Geländemodelle (DGM), Orthofotos etc., abgeleitet werden. Die Ergebnisse der Luftbildphotogrammetrie dienen der Erstellung und Fortführung topographischer Karten und Orthofotos, der großmaßstäbigen Punktbestimmung in Liegenschaftskatastern und zur Flurbereinigung. Es können auch digitale Geländemodelle (DGM) aus den Daten abgeleitet werden. Die Landnutzungserhebung sowie Umwelt- und Leitungskataster profitieren ebenfalls von den Resultaten der Luftbildphotogrammetrie.

Nahbereichsphotogrammetrie

Ein Anwendungsbeispiel aus der Paläontologie: Die mittlere Teilabbildung zeigt das farbcodierte Relief einer Sedimentgesteinsschichtfläche mit Dinosauriertrittsiegeln, das auf einem photogrammetrischen 3D-Modell dieser Schichtfläche basiert.

Die Nahbereichsphotogrammetrie befasst sich mit Objekten in einem Größenbereich von wenigen Zentimetern bis zu rund 100 Metern.

Die einfachste Methode besteht darin, ein Objekt mit einem Vergleichsmaßstab zusammen zu fotografieren. Dieser Maßstab kann aus Papier, Pappe, Kunststoff usw. gefertigt sein. Für größere Objekte sind Nivellierlatten denkbar. Diese Methode wird in der medizinischen Dokumentation, der Archäologie, Spurensicherung und Forensik angewendet. Durch Vergleich des Objektes mit dem Maßstab kann dessen tatsächliche Größe errechnet werden.

In der Nahbereichsphotogrammetrie gibt es, anders als in der Luftbildphotogrammetrie, keine Einschränkungen bei der Aufnahmeanordnung. Es können beliebige Aufnahmepositionen verwendet werden, wie sie entstehen, wenn man ein Objekt mit einer Handkamera von mehreren Richtungen fotografiert. In der Regel benutzt man dazu heute hochauflösende Digitalkameras.

Die häufigsten Anwendungsfelder der Nahbereichsphotogrammetrie sind die industrielle Messtechnik (s. Streifenprojektion), Medizin und Biomechanik sowie die Unfallphotogrammetrie. In der Architektur und Archäologie nutzt man die Nahbereichsphotogrammetrie zur Bauaufnahme, also zur Dokumentation als Grundlage von Umbauten und denkmalpflegerischen Maßnahmen.

Ein wichtiges Nebenprodukt der Nahbereichsphotogrammetrie sind entzerrte Fotografien. Das sind Fotografien von nahezu ebenen Objekten wie Gebäudefassaden, die so auf eine Fläche projiziert werden, dass die Abstände im Bild über einen einfachen Maßstab in metrische Längen und Abstände umgerechnet werden können.

In jüngster Zeit hat auch die moderne Kinematographie Techniken aus der Photogrammetrie übernommen. Im Film Fight Club von 1999 wurden mit dieser Technik zum Beispiel interessante Kamerafahrten ermöglicht. Mit Veröffentlichung des Films Matrix im selben Jahr erregte das Bullet-Time-Verfahren erstmals weltweite Aufmerksamkeit.

Anwendung in der Archäologie

Die technisch weiterentwickelte Photogrammetrie ermöglicht es, aus zweidimensionalen Aufnahmen 3D-Daten zu gewinnen. Gegenüber den herkömmlichen 3D-Scan-Verfahren bietet die Photogrammetrie einige, für spezielle Fragestellungen, wichtige Vorzüge. So können schwer zugängige Bereiche in Fundplätzen auch aus der Entfernung dokumentiert werden. Große Datenmengen mit hoher Datendichte lassen sich schnell zusammenstellen, auch eignet sich das Verfahren für die Dokumentation von sehr kleinen Objekte bis hin zu großen Gebäuden oder ganzen Landschaften gleichermaßen. Aus dem gewonnenen Datensatz können sowohl sehr kleine und genaue wie auch große und grobe Modelle generiert werden, damit stehen die digitalisierten Fotografien für weitere Anwendungsbereiche und Fragestellungen zur Verfügung. Die Datenaufnahme stellt gleichzeitig die Dokumentation des Vermessungsprozesses dar. Auf dieser Grundlage kann der Prozess der Modellgenerierung kontrolliert und die Berechnungen bei Bedarf neu angepasst werden.[10][11]

Siehe auch

Deutsche Gesellschaft für Photogrammetrie, Fernerkundung und Geoinformation (DGPF) e.V.

Literatur

Konsortium Luftbild G.m.b.H. – Stereographik G.m.b.H. München (Hrsg.): Die photogrammetrische Geländevermessung. Selbstverlag, München 1922.
Karl Kraus: Photogrammetrie. de Gruyter, Berlin 2004, ISBN 3-11-017708-0
Thomas Luhmann: Nahbereichsphotogrammetrie. Wichmann, Heidelberg 2003, ISBN 3-87907-398-8
McGlone, Mikhail, Bethel (Hrsg.): Manual of Photogrammetry. ASPRS, Bethesda MD ⁵2004, ISBN 1-57083-071-1
Alparslan Akça, Jürgen Huss (Hrsg.) et al.: Luftbildmessung und Fernerkundung in der Forstwirtschaft. Wichmann, Karlsruhe 1984, ISBN 3-87907-131-4
Schweizerische Gesellschaft für Photogrammetrie, Bildanalyse und Fernerkundung (Hrsg.): Photogrammetrie in der Schweiz. Tümmler, Bonn 1996, ISBN 3-427-78721-4

Weblinks

Wiktionary: Photogrammetrie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Jens Petersen: Photogrammetrie bei der Verkehrsunfallaufnahme. Archiviert vom Original am 25. Januar 2017; abgerufen am 9. Juni 2021.
Schweizerische Gesellschaft für Photogrammmetrie in der Archivdatenbank des Schweizerischen Bundesarchivs

Fachverbände

Einzelnachweise

Luhmann, Thomas: Nahbereichsphotogrammetrie Grundlagen, Methoden und Anwendungen. 3., völlig neu bearb. und erw. Auflage. Wichmann, Berlin 2010, ISBN 978-3-87907-479-2.
Orel Eduard von. In: Österreichisches Biographisches Lexikon 1815–1950 (ÖBL). Band 7, Verlag der Österreichischen Akademie der Wissenschaften, Wien 1978, ISBN 3-7001-0187-2, S. 243 f. (Direktlinks auf S. 243, S. 244).
Albrecht Meydenbauer: Die Photometrographie. In: Wochenblatt des Architektenvereins zu Berlin Jg. 1, 1867, Nr. 14, S. 125–126 (Digitalisat); Nr. 15, S. 139–140 (Digitalisat); Nr. 16, S. 149–150 (Digitalisat).
Die Photogrammetrie. In: Wochenblatt des Architektenvereins zu Berlin Jg. 1, 1867, Nr. 49, S. 471–472 (Digitalisat).
Wochenblatt des Architektenvereins zu Berlin. Jg. 1, 1867, Nr. 49, S. 471, Fußnote.
Zeitschrift für Vermessungswesen. 26, 1892, S. 220 (Digitalisat) unter Bezug auf seinen Aufsatz Über die Verwertung der Photographie zu geometrischen Aufnahmen (Photogrammetrie). In: Zeitschrift für Vermessungswesen 5, 1876, S. 1–17 (Digitalisat).
Deutsche Bauzeitung 26. Jg. 1892, Nr. 50, S. 300 (Digitalisat). Siehe Albrecht Grimm: Der Ursprung des Wortes Photogrammetrie. In: Internationales Archiv für Photogrammetrie Bd. 23, 1980, S. 323–330; Albrecht Grimm: The Origin of the Term Photogrammetry. In: Dieter Fritsch (Hrsg.): Proceedings of 51st photogrammetric week. Berlin 2007, S. 53–60 (Digitalisat).
Meyers Lexikon (Memento vom 12. November 2006 im Internet Archive)
K.Kraus 2004, F.K. List 1998.
Maren Lindstaedt, Thomas Kersten, Martin Sauerbier, Janine Peterhans, Peter Fux: Terrestrisches Laserscanning und digitale Photogrammetrie zur archäologischen Dokumentation der Petroglyphen von Chichictara in Peru. In: Thomas Luhmann, Christina Müller (Hrsg.): Photogrammetrie, Laserscanning, Optische 3D-Messtechnik – Beiträge der Oldenburger 3D-Tage 2007, Wichmann Verlag, Heidelberg, S. 328–337. ( auf hcu-hamburg.de) hier S. 334 f.
Günter Eckstein: Photogrammetrische Vermessungen bei archäologischen Ausgrabungen. Denkmalpflege in Baden-Württemberg, 23. Juli 2014, Ausgabe Bd. 11 Nr. 2 (1982), S. 60–67 ( auf journals.ub.uni-heidelberg.de)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Luhmann, Thomas: Nahbereichsphotogrammetrie Grundlagen, Methoden und Anwendungen. 3., völlig neu bearb. und erw. Auflage. Wichmann, Berlin 2010, ISBN 978-3-87907-479-2.

[2] Orel Eduard von. In: Österreichisches Biographisches Lexikon 1815–1950 (ÖBL). Band 7, Verlag der Österreichischen Akademie der Wissenschaften, Wien 1978, ISBN 3-7001-0187-2, S. 243 f. (Direktlinks auf S. 243, S. 244).

[3] Albrecht Meydenbauer: Die Photometrographie. In: Wochenblatt des Architektenvereins zu Berlin Jg. 1, 1867, Nr. 14, S. 125–126 (Digitalisat); Nr. 15, S. 139–140 (Digitalisat); Nr. 16, S. 149–150 (Digitalisat).

[4] Die Photogrammetrie. In: Wochenblatt des Architektenvereins zu Berlin Jg. 1, 1867, Nr. 49, S. 471–472 (Digitalisat).

[5] Wochenblatt des Architektenvereins zu Berlin. Jg. 1, 1867, Nr. 49, S. 471, Fußnote.

[6] Zeitschrift für Vermessungswesen. 26, 1892, S. 220 (Digitalisat) unter Bezug auf seinen Aufsatz Über die Verwertung der Photographie zu geometrischen Aufnahmen (Photogrammetrie). In: Zeitschrift für Vermessungswesen 5, 1876, S. 1–17 (Digitalisat).

[7] Deutsche Bauzeitung 26. Jg. 1892, Nr. 50, S. 300 (Digitalisat). Siehe Albrecht Grimm: Der Ursprung des Wortes Photogrammetrie. In: Internationales Archiv für Photogrammetrie Bd. 23, 1980, S. 323–330; Albrecht Grimm: The Origin of the Term Photogrammetry. In: Dieter Fritsch (Hrsg.): Proceedings of 51st photogrammetric week. Berlin 2007, S. 53–60 (Digitalisat).

[8] Meyers Lexikon (Memento vom 12. November 2006 im Internet Archive)

[9] K.Kraus 2004, F.K. List 1998.

[10] Maren Lindstaedt, Thomas Kersten, Martin Sauerbier, Janine Peterhans, Peter Fux: Terrestrisches Laserscanning und digitale Photogrammetrie zur archäologischen Dokumentation der Petroglyphen von Chichictara in Peru. In: Thomas Luhmann, Christina Müller (Hrsg.): Photogrammetrie, Laserscanning, Optische 3D-Messtechnik – Beiträge der Oldenburger 3D-Tage 2007, Wichmann Verlag, Heidelberg, S. 328–337. ( auf hcu-hamburg.de) hier S. 334 f.

[11] Günter Eckstein: Photogrammetrische Vermessungen bei archäologischen Ausgrabungen. Denkmalpflege in Baden-Württemberg, 23. Juli 2014, Ausgabe Bd. 11 Nr. 2 (1982), S. 60–67 ( auf journals.ub.uni-heidelberg.de)