Streifenprojektion
Die Streifenprojektion, manchmal auch als Streifenlichtscanning und selten als Streifenlichttopometrie bezeichnet, umfasst optische Messmethoden, bei der Bildsequenzen zur dreidimensionalen Erfassung von Oberflächen verwendet werden. Es ist neben dem Laserscanning ein 3D-Scan-Verfahren, das es ermöglicht, die Oberflächenform von Objekten berührungslos zu digitalisieren und dreidimensional darzustellen. Im Prinzip funktionieren solche Verfahren so, dass mit einem Projektor strukturiertes Licht (z. B. Streifen) auf das zu messende Objekt projiziert wird, und von (mindestens) einer Kamera aufgenommen wird. Wenn man die gegenseitige Lage des Projektors und der Kamera kennt, kann man die – in die Kamera – abgebildeten Punkte entlang eines Streifens mit der bekannten Ausrichtung des Streifens vom Projektor zum Schnitt bringen, und deren dreidimensionale Position berechnen (s. Abb. 1).[1]
Überblick der Streifenprojektionsverfahren
Die Streifenprojektionsverfahren unterscheiden sich darin, dass sie mit unterschiedlich projiziertem bzw. codiertem Licht arbeiten, und in der Art und Weise, wie die verschiedenen Projektionsmuster in den Bildern identifiziert werden.
Messprinzip
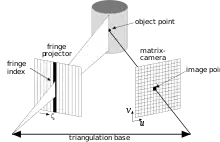
Das Messprinzip ist dem menschlichen räumlichen Sehen nachempfunden, wobei ein dreidimensionales Objekt von zwei Augen betrachtet wird, die einen Abstand zueinander haben (s. stereoskopisches Sehen). Der Projektor ersetzt eines der beiden Augen, indem es einen Lichtstrahl auf das Messobjekt projiziert, wodurch ein Oberflächenpunkt beleuchtet wird.
Aufbau eines Streifenlicht-Scanners
In der technischen Umsetzung besteht ein Streifenlicht-Scanner, der mit dem Prinzip der Streifenprojektion arbeitet, aus mindestens einem Musterprojektor, der im Prinzip einem Diaprojektor ähnelt, sowie aus mindestens einer digitalen Videokamera, welche auf einem Stativ montiert sind. Bei kommerziellen Systemen haben sich mittlerweile Aufbauten mit einem Projektor und einer oder zwei Kameras etabliert.
Ablauf einer Messung
Der Projektor beleuchtet das Messobjekt zeitlich sequentiell mit Mustern von parallelen hellen und dunklen Streifen unterschiedlicher Breite (s. Abb. 3). Die Kamera(s) registrieren das projizierte Streifenmuster unter einem bekannten Blickwinkel zur Projektion. Für jedes Projektionsmuster wird mit jeder Kamera ein Bild aufgenommen. Für jeden Bildpunkt aller Kameras entsteht so eine zeitliche Folge von unterschiedlichen Helligkeitswerten.
Berechnung der Oberflächenkoordinaten
Vor der eigentlichen Berechnung muss man die korrekte Streifennummer im Bild der Kamera identifizieren, um sie einer Bildposition zuordnen zu können.
Projektor und Kamera bilden die Basis eines Dreiecks, und der projizierte Lichtstrahl vom Projektor und der rückprojizierte Bildpunkt der Kamera bilden die Seiten des Dreiecks (s. Abb. 1). Kennt man die Basislänge und die Winkel zwischen den Lichtstrahlen und der Basis, kann man den Ort des Schnittpunktes mittels Dreiecksberechnung bestimmen, was als Triangulationsverfahren bezeichnet wird. Die exakte Berechnung der Strahlen erfolgt mit dem aus der Photogrammetrie bekannten Bündelausgleichungsverfahren.
Auf diesem Prinzip beruhen alle nachfolgenden Verfahren.
Lichtschnittverfahren
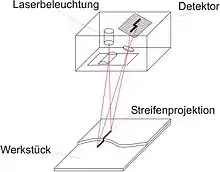
Beim Lichtschnittverfahren wird ein ebenes Lichtbündel auf das zu messende Objekt projiziert (s. Abb. 2). Dieses Lichtbündel erzeugt eine helle Linie auf dem Objekt. Aus der Blickrichtung des Projektors ist diese Linie exakt gerade. Aus der seitlichen Sicht der Video-Kamera sieht man sie – aufgrund der perspektivischen Verzerrung – durch die Objektgeometrie deformiert. Die Abweichung von der Geradheit im Kamerabild ist ein Maß für die Objekthöhe.
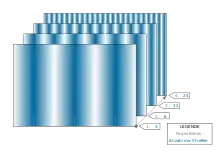
Das Verfahren wird oft erweitert, indem man gleichzeitig viele parallele Linien, also ein Liniengitter aufs Messobjekt projiziert. Die korrekte Streifennummer wird dann durch Auszählen und Identifizieren der entsprechenden Gitterlinie im Bild wiedergefunden.
Unstetigkeiten in der Objektoberfläche führen zu Problemen bei der eindeutigen Zuordnung. Um eventuelle Fehlzuordnungen zu vermeiden, verwendet man einen hierarchischen Ansatz (s. Abb. 3). D. h., man macht mehrere Aufnahmen, und variiert das Streifenmuster mit jeweils unterschiedlicher Streifenanzahl. Man beginnt mit einer niedrigen Anzahl "grober" Streifen und erhöht für jedes Bild die Anzahl der Streifen, wodurch die Streifen immer feiner werden.[1]
Codierter Lichtansatz

Die Auflösung der Mehrdeutigkeiten ist vor allem bei unstetigen Oberflächen problematisch. Mit Hilfe des codierten Lichtansatzes kann man die Mehrdeutigkeiten auflösen und hat damit eine absolut messende Methode.[1] Es gibt unterschiedlich codierte Lichtmuster, welche hierbei zum Einsatz kommen.
Eine Möglichkeit ist ganz ähnlich, wie die zuvor erwähnte Grob-zu-Fein-Strategie. Der Unterschied ist, dass anstatt einer kontinuierlichen sinusförmigen Hell-Dunkel-Folge eine binär-codierte Folge mit harten Kanten verwendet wird. Diese hintereinander projizierten Lichtcode-Muster werden von einer synchron geschalteten Kamera aufgenommen. Dadurch enthält jede Position im projizierten Lichtmuster eine eindeutige Binärcode-Folge, welche man dann in den Bildern einer entsprechenden Bildposition zuordnen kann. Anders gesagt: Betrachtet man ein einzelnes Bildelement in der Kamera, so „sieht“ dieses Bildelement eine eindeutige Hell-Dunkel-Folge, die sich über eine Tabelle eindeutig genau derjenigen Projektionslinie zuordnen lässt, die das Oberflächenelement beleuchtete.
Andere Lichtcodes sind z. B. zufällige (stochastische) Muster (s. Abb. 4). Die Zuordnung des Projektionsmusters zur korrekten Bildposition erfolgt durch Auswahl eines kleinen Ausschnitts vom Projektionsmuster und Abgleich mit dem Bild (image matching). Im Bereich Computer Vision und Photogrammetrie ist dies ein wichtiges Verfahren und dort als Korrespondenzproblem bekannt und Gegenstand intensiver Forschung. Da die gegenseitige Lage des Projektors und der Kamera bekannt sind, kann man – zur Eingrenzung des Suchraumes – die Epipolargeometrie vorteilhaft nutzen. Dadurch werden Fehlzuordnungen (weitestgehend) vermieden und die Zuordnung deutlich beschleunigt.
Phasenschiebeverfahren
Eine höhere Genauigkeit ist mit dem Phasenschiebeverfahren (auch dynamische Streifenprojektion oder phase-shift genannt) zu erreichen. Hierbei wird das projizierte Streifengitter als sinusförmige Funktion aufgefasst. Bei kleinen Höhenänderungen verschiebt sich eine Hell-Dunkel-Kante im Kamerabild nur um Bruchteile einer Gitterperiode (s. Abb. 2). Wie schon im Abschnitt Lichtschnittverfahren erwähnt, wird eine auf das Objekt projizierte Linie durch die Objektgeometrie deformiert. Die Abweichung von dieser Linie im Kamerabild ist ein Maß für die Objekthöhe.
Weist das Projektionsgitter eine sinusförmige Helligkeitsmodulation auf, so signalisiert ein Bildelement in der Kamera eine sinusförmige Änderung. Verschiebt man das Projektionsgitter im Projektor um eine Viertelperiode, so wird das Bildelement nun eine kosinusförmige Abhängigkeit von der Objekthöhe ausgeben. Der Quotient aus beiden Signalen entspricht somit dem Tangens der durch die Höhenänderung bewirkten Verschiebung. Mit einer Lookup-Tabellenoperation kann daraus der Arkustangens effizient bestimmt werden. Dieser stellt als Winkel- bzw. Phaseninformation die Verschiebung in Bruchteilen der Gitterperiode dar.[1]
Das Phasenschiebeverfahren kann entweder als Ergänzung eines Gray-Codes oder als absolut messendes Heterodynverfahren eingesetzt werden.
Praktische Aspekte
Ein Streifenprojektionsscanner muss vor der Anwendung kalibriert werden (s. #Kalibrierung). Kommerziell erwerbliche Geräte sind normalerweise schon kalibriert. Die erfassten Oberflächeninformationen werden in Form von Punktwolken oder Freiformflächen dokumentiert.
Kalibrierung
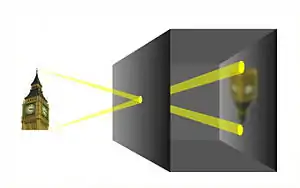
Wichtig für die Berechnung der Koordinaten und die garantierte Genauigkeit der Ergebnisse ist eine präzise Kalibrierung der Abbildungseigenschaften. Alle Abbildungseigenschaften von Projektoren und Kameras werden mit Hilfe eines mathematischen Modells beschrieben. Als Basis dient eine einfache Lochkamera, bei der alle Bildstrahlen vom Objektpunkt im dreidimensionalen Raum durch einen gemeinsamen Punkt, das Projektionszentrum, laufen und in den zugehörigen Bildpunkt auf dem Sensor oder Film abgebildet werden.
Zusätzlich müssen die in diesem Modell nicht idealen Eigenschaften von realen Linsensystemen, die in Verzerrungen des Bildes resultieren, durch eine Verzeichnungskorrektur angepasst werden.
Die genannten Parameter der Lochkamera sowie ihre Lage und Orientierung im Raum werden aus einer Serie von Kalibrieraufnahmen mit photogrammetrischen Methoden insbesondere mit einer Bündelausgleichsrechnung bestimmt.
Kombinieren mehrerer Scanns (Navigation)
Eine einzelne Messung mit dem Streifenprojektionsscanner ist in ihrer Vollständigkeit durch die Sichtbarkeit der Objektoberfläche eingeschränkt. Damit ein Punkt der Oberfläche erfasst werden kann, muss er vom Projektor beleuchtet und von den Kameras beobachtet werden. Punkte, die beispielsweise auf der Rückseite des Objektes liegen, müssen in einer separaten Messung erfasst werden.
Für ein komplexes Objekt können sehr viele (einige hundert) Einzelmessungen für die komplette Erfassung notwendig sein. Damit man die Ergebnisse aller Messungen in ein gemeinsames Koordinatensystem zusammenführen kann, sind folgende Methoden gebräuchlich: das Anbringen von punktförmigen Markern auf dem Objekt als Passpunkte, die Korrelation von Objektmerkmalen, oder die genaue Messung der Sensorposition mit einem zusätzlichen Messsystem. Dieser Prozess wird unter Fachleuten als Navigation bezeichnet.
Genauigkeit
Die erreichbare Messgenauigkeit ist proportional zur dritten Wurzel aus dem Messvolumen. Kommerzielle Systeme, welche im Bereich Reverse Engineering eingesetzt werden, erreichen Genauigkeiten von 0,003 mm bis 0,3 mm je nach technischem Aufwand und Messvolumen. Systeme mit mikroskopischen Messfeldern unterhalb 1 cm² können zur Beurteilung von Mikrogeometrien, wie z. B. Radien an Schneidkanten oder der Beurteilung von Mikrostrukturen eingesetzt werden und erreichen dort Messgenauigkeiten unterhalb 1 µm.
Anwendungen
Verfahren, die mit projiziertem Licht arbeiten, kommen meist dann zum Einsatz, wenn besonders hohe Genauigkeit gefordert wird oder die Oberfläche keine Textur aufweist. Neben Anwendungen in der Medizin, Zahntechnik und Pathologie werden Streifenprojektionscanner hauptsächlich in der Industrie, im Designprozess für neue Produkte (Reverse Engineering) und bei der Formkontrolle von Werkstücken und Werkzeugen (Soll-Ist-Vergleich) verwendet. Mit mehreren tausend in Deutschland installierten Systemen (geschätzter Stand April 2005) sind sie in der Automobil- und Flugzeugindustrie sehr weit verbreitet und stellen in vielen Anwendungsfällen eine bevorzugte Alternative zu mechanischen Koordinatenmessgeräten dar.
Tatortvermessung
Mit Hilfe von Streifenlichtscannern in Flächenkameras tasten Kriminaltechniker einen Tatort dreidimensional ab und erstellen so ein 3D-Bild vom Tatort, das genau analysiert und auf Spuren hin abgesucht werden kann, ohne dass die polizeiliche Tatortgruppe das Gelände betreten muss und möglicherweise Beweismittel verfälscht oder vernichtet. Eine Teilanwendung davon ist die dreidimensionale Abtastung von Bodenabdrücken und Fußspuren, die gegenüber dem früheren Ausgießen mit Gips den Vorteil hat, dass die Spurensicherung berührungslos erfolgt und der Abdruck beliebig oft vervielfältigt werden kann.
Reverse Engineering
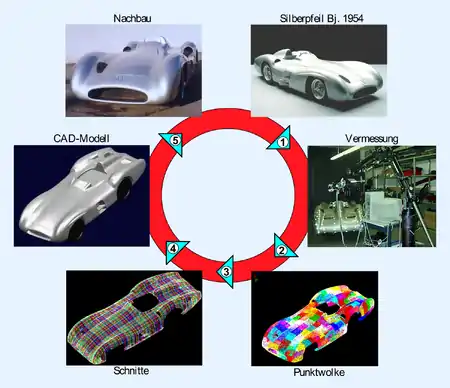
Das nebenstehende Beispiel erläutert den Reverse-Engineering-Prozess am Beispiel eines historischen Rennwagens: Der Silberpfeil W196, Baujahr 1954. Vom Original (1) wurde in 14 Stunden Messzeit eine Punktewolke (2) mit 98 Millionen Messpunkten erzeugt. Diese wurden auf achsparallele Schnitte im Abstand von zwei Zentimetern reduziert (3), auf denen in etwa 80 Arbeitsstunden ein CAD-Modell (4) konstruiert wurde. Auf Basis des CAD-Modells wurde schließlich ein Nachbau (5) im Maßstab 1:1 angefertigt, der heute im Mercedes-Benz Museum in Stuttgart-Untertürkheim zu besichtigen ist.
Wunddokumentation
Die Wunddokumentation mittels Streifenlichttopometrie zeigt sich gegenüber allen in der gerichtsmedizinischen Praxis angewandten abbildenden Verfahren als überlegen, da sie die räumliche, metrisch exakte Darstellung mit realistischen Farben einzelner relevanter Punkte einer Verletzung ermöglicht. Das Resultat ist ein „digitaler Wundenmensch“ und erlaubt die Objektivierung der äußeren Leichenschau.
Anwendungsbeispiele in der Archäologie, Denkmalpflege und Industrie
Folgende Liste gibt einen Überblick über Anwendungsfälle von diesem Verfahren:
- berührungslose und objektschonende 3D-Sicherungsdokumentation von Kunst- und Kulturgütern[2]
- Qualitätskontrolle von Maschinenbauteilen[3]
- virtuelle Rekonstruktion von zerstörten Objekten[4]
- Sichtbarmachung von schwer lesbaren Inschriften[5]
- Animation von Sachverhalten[6]
- Reproduktion bzw. Erstellung von physischen Kopien mittels Rapid Prototyping Verfahren[7]
- Fertigung von Museumsrepliken[8]
Siehe auch
Literatur
- G. Frankowski, M. Chen, T. Huth: Real-time 3D Shape Measurement with Digital Stripe Projection by Texas Instruments Micromirror Devices (DMD). In: Proc. Of SPIE. Vol. 3958 (2000), S. 90–106.
- G. Frankowski, M. Chen, T. Huth: Optical Measurement of the 3D-Coordinates and the Combustion Chamber Volume of Engine Cylinder Heads. In: Proc. Of "Fringe 2001". S. 593–598.
- Fringe 2005. The 5th International Workshop on Automatic Processing of Fringe Patterns. Springer, Berlin 2006, ISBN 3-540-26037-4.
- C. Hof, H. Hopermann: Comparison of Replica- and In Vivo-Measurement of the Microtopography of Human Skin. University of the Federal Armed Forces, Hamburg.
- Klaus Körner, Ulrich Droste: Tiefenscannende Streifenprojektion (DSFP) University of Stuttgart.
- Christian Kohler, Klaus Körner: Streifentriangulation mit räumlichen Lichtmodulatoren. Universität Stuttgart.
- T. Peng, S. K. Gupta, K Lau: Algorithms for constructing 3-D point clouds using multiple digital fringe projection patterns. (PDF; 2,0 MB). CAD Conf., Bangkok, Thailand, Juni 2005.
- Elena Stoykova, Jana Harizanova, Venteslav Sainov: Pattern Projection Profilometry for 3D Coordinates Measurement of Dynamic Scenes. In: Three Dimensional Television. Springer, 2008, ISBN 978-3-540-72531-2.
- Verfahren zur optischen 3D-Vermessung spiegelnder Oberflächen: KIT Scientific Publishing (29. Januar 2008)
- Herbert Wichmann: Photogrammetrie – Laserscanning – Optische 3D-Messtechnik: Beiträge der Oldenburger 3D-Tage 2006, Online-Version (abgerufen am 12. Juni 2020)
- W. Wilke: Segmentierung und Approximation großer Punktwolken. Dissertation. Univ. Darmstadt, 2000. (PDF; 4,5 MB).
- G. Wiora: Optische 3D-Messtechnik Präzise Gestaltvermessung mit einem erweiterten Streifenprojektionsverfahren. Dissertation. Univ. Heidelberg, 2001.
- Song Zhang, Peisen Huang: High-resolution, Real-time 3-D Shape Measurement. PhD Dissertation. Harvard Univ., 2005. (PDF; 8,1 MB)
Einzelnachweise
- Luhmann, Thomas: Nahbereichsphotogrammetrie Grundlagen, Methoden und Anwendungen. 3., völlig neu bearb. und erw. Auflage. Wichmann, Berlin 2010, ISBN 978-3-87907-479-2.
- Sicherung des Weltkulturerbes: 3D-Scannen statt Zeichnen
- Trigonart: 3D-Scan Reverse Engineering U-Boot
- Pressemitteilung WS: Virtuelle Rekonstruktion und Animation der Hathorkapelle
- Inschrift aus Gisela-Grab entziffert, Meldung vom 7. November 2016, abgerufen am 15. November 2016
- L.I.S.A. - Das Wissenschaftsportal der Gerda Henkel Stiftung: 3D-Scannen statt Zeichnen
- 3Druck.com: Antike aus der Retorte: Detailgetreues Tempelmodell aus dem 3D-Drucker
- Archäologie Online: Das neue Abbild der Schönen