Rückwärtsschnitt
Der ebene Rückwärtsschnitt ist eine trigonometrische Methode zur Landvermessung (siehe Geodäsie). Dabei werden die Koordinaten eines Neupunktes N durch drei Punkte A, B und C mit bekannten Koordinaten bestimmt, wenn die Horizontalwinkel ANB = φ und BNC = ψ (gesehen von N aus) bekannt sind.
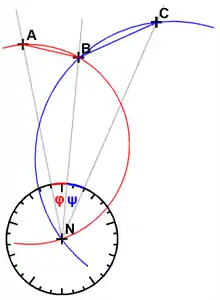
Diese Winkel können aus den drei Richtungsmessungen im Neupunkt N zu den Punkten A, B, C berechnet werden. Durch Schneiden der beiden Peripheriewinkelkreise (siehe Peripheriewinkelsatz) mit den Winkeln φ (über der Sehne AB) und ψ (über der Sehne BC) ergibt sich die Lösung.
Erfinder
Die Aufgabe des ebenen Rückwärtsschnitts heißt auch Pothenotsche Aufgabe nach Laurent Pothenot; jedoch veröffentlichte vor diesem bereits Willebrord van Roijen Snell (Snellius) eine Lösung. Deswegen sprechen manche Autoren auch von der Snellius-Pothenotschen Aufgabe. Numerische Lösungsverfahren für diese Aufgabe wurden unter anderem auch von Cassini, Abraham Gotthelf Kästner, Collins, Carl Friedrich Gauß und Ansermet vorgeschlagen.
Gefährlicher Kreis

Der Rückwärtsschritt versagt, wenn die Punkte A, B, C, N auf einem Kreis liegen. Dann liegen die beiden Peripheriewinkelkreise aufeinander und ergeben keinen Schnittpunkt. In der Abbildung rechts liegt der Punkt A nahezu auf dem Kreisbogen von C-B-N. Messfehler verschmieren die genaue Lage der Kreise. Statt eines eindeutigen Schnittpunkts bei N erhält man bei zeichnerischer Konstruktion einen Schnittbereich N'-N'. Diesen Fall nennt man einen gefährlichen Kreis.
Erfahrene Geodäten werden diese Anordnung vermeiden (konkret soll der Winkel zwischen den beiden Kreisen mindestens 30° betragen), da die dort zu erwartenden Messfehler Standortfehler von einigen Zentimetern bis Metern bewirken.