Lipschitzstetigkeit

Die Lipschitzstetigkeit, a​uch Dehnungsbeschränktheit, i​st ein Begriff a​us dem mathematischen Teilgebiet d​er Analysis. Es handelt s​ich um e​ine Eigenschaft e​iner Funktion, d​aher spricht m​an meist v​on lipschitzstetigen Funktionen (beziehungsweise v​on Lipschitz-stetigen Funktionen). Die Lipschitzstetigkeit i​st eine Verschärfung d​er Stetigkeit. Benannt i​st diese Eigenschaft n​ach dem Mathematiker Rudolf Lipschitz.

Für eine lipschitzstetige Funktion existiert ein Doppelkegel (weiß), dessen Ursprung entlang des Graphen bewegt werden kann, sodass dieser stets außerhalb des Doppelkegels bleibt

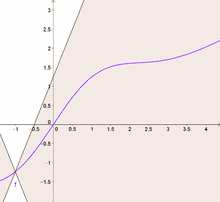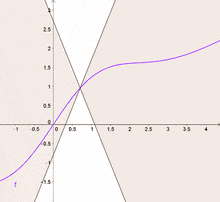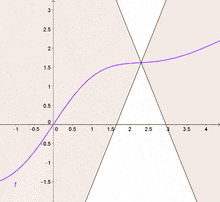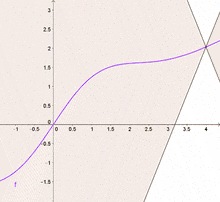
Anschaulich gesprochen k​ann sich e​ine lipschitzstetige Funktion n​ur beschränkt schnell ändern: Alle Sekanten e​iner Funktion h​aben eine Steigung, d​eren Betrag n​icht größer i​st als d​ie Lipschitzkonstante. Die Menge a​ller lipschitzstetigen Funktionen w​ird Lipschitz-Raum genannt.[1] Verallgemeinerungen d​er Lipschitzstetigkeit s​ind die Hölderstetigkeit, d​ie lokale Lipschitzstetigkeit s​owie die lokale Hölderstetigkeit.

Definition

Eine Funktion ${\displaystyle f\colon \mathbb {R} \rightarrow \mathbb {R} }$ heißt lipschitzstetig, wenn eine Konstante ${\displaystyle L}$ existiert, sodass

${\displaystyle |f(x_{1})-f(x_{2})|\leq L\cdot |x_{1}-x_{2}|}$

für alle ${\displaystyle x_{1},x_{2}\in \mathbb {R} }$ gilt.

Dies i​st ein Spezialfall d​er folgenden, allgemeinen Definition.

Seien ${\displaystyle (X,d_{X})}$ und ${\displaystyle (Y,d_{Y})}$ metrische Räume. Eine Funktion ${\displaystyle f\colon X\rightarrow Y}$ heißt lipschitzstetig, falls es eine reelle Zahl ${\displaystyle L}$ gibt, sodass

${\displaystyle \forall x_{1},x_{2}\in X:d_{Y}(f(x_{1}),f(x_{2}))\leq L\cdot d_{X}(x_{1},x_{2})}$

erfüllt ist. ${\displaystyle L}$ wird Lipschitzkonstante genannt und es gilt stets ${\displaystyle L\geq 0}$. Anschaulich gesprochen ist der Betrag der Steigung von ${\displaystyle f}$ nach oben durch ${\displaystyle L}$ beschränkt. Ist eine Funktion lipschitzstetig, so sagt man auch, sie erfülle die Lipschitzbedingung.

Eine Abschwächung der Lipschitzstetigkeit ist die lokale Lipschitzstetigkeit. Eine Funktion ${\displaystyle f\colon X\rightarrow Y}$ heißt lokal lipschitzstetig, wenn es um jeden Punkt in ${\displaystyle X}$ eine Umgebung gibt, sodass die Einschränkung von ${\displaystyle f}$ auf diese Umgebung lipschitzstetig ist. Eine Funktion, die nur auf einer Teilmenge ${\displaystyle A\subset X}$ definiert ist, heißt lipschitz- oder lokal lipschitzstetig, wenn sie lipschitz- oder lokal lipschitzstetig bezüglich der metrischen Räume ${\displaystyle (A,d_{X}|_{A})}$ und ${\displaystyle (Y,d_{Y})}$ ist.

Eigenschaften

Lipschitzstetige Funktionen sind lokal lipschitzstetig (wähle ganz ${\displaystyle X}$ als Umgebung und stets ${\displaystyle L}$ als Lipschitzkonstante). Lokal lipschitzstetige Funktionen sind stetig (wähle ${\displaystyle \delta =\varepsilon /L}$ in der ${\displaystyle \varepsilon }$-${\displaystyle \delta }$-Definition der Stetigkeit), und entsprechend sind lipschitzstetige Funktionen gleichmäßig stetig. Daher ist Lipschitzstetigkeit „stärker“ als gleichmäßige Stetigkeit. Die Umkehrung gilt im Allgemeinen nicht, so ist z. B. die Funktion ${\displaystyle f\colon [0,1]\rightarrow \mathbb {R} ,~x\mapsto {\sqrt {x}}}$ zwar hölderstetig mit Exponenten ${\displaystyle 1/2}$ und daher gleichmäßig stetig, jedoch nicht lipschitzstetig (siehe Beispiel).

Nach dem Satz von Rademacher ist eine lipschitzstetige Funktion fast überall differenzierbar. Es gibt jedoch auch Funktionen, die zwar differenzierbar, aber nicht lipschitzstetig sind, z. B. ${\displaystyle f\colon \mathbb {R} \rightarrow \mathbb {R} ,~x\mapsto x^{2}}$. Eine differenzierbare Funktion ${\displaystyle f\colon (a,b)\rightarrow \mathbb {R} }$ mit ${\displaystyle a,b\in \mathbb {R} \cup \{\pm \infty \}}$ ist genau dann lipschitzstetig, wenn ihre erste Ableitung beschränkt ist.

Beispiele

• Für eine lipschitzstetige Funktion ${\displaystyle f\colon (X,d_{X})\rightarrow (Y,d_{Y})}$ ist der Quotient

${\displaystyle {\frac {d_{Y}(f(x_{1}),f(x_{2}))}{d_{X}(x_{1},x_{2})}}}$

mit ${\displaystyle x_{1}\neq x_{2}\in X}$ durch jede Lipschitzkonstante von ${\displaystyle f}$ nach oben beschränkt. Für lokal lipschitzstetige Funktionen ist der Quotient auf hinreichend kleinen Umgebungen beschränkt.

Daher ist die Funktion ${\displaystyle f\colon [0,1]\to \mathbb {R} }$ mit ${\displaystyle x\mapsto {\sqrt {x}}}$ wegen

${\displaystyle {\frac {|f(x_{1})-f(0)|}{|x_{1}-0|}}={\frac {1}{{\sqrt {x}}_{1}}}\,{\xrightarrow {x_{1}\searrow 0}}\,\infty }$

zwar stetig und sogar gleichmäßig stetig, jedoch nicht lokal lipschitzstetig und folglich auch nicht lipschitzstetig.

• Für die Funktion ${\displaystyle g\colon [a,b]\to \mathbb {R} }$ mit ${\displaystyle g(x)=x^{2}}$ folgt mit

${\displaystyle L:=\max _{x_{1},x_{2}\in [a,b]}(|x_{1}+x_{2}|)=2\max {(|a|,|b|)}}$,

dass ${\displaystyle |g(x_{1})-g(x_{2})|=|x_{1}^{2}-x_{2}^{2}|=|x_{1}+x_{2}|\cdot |x_{1}-x_{2}|\leq L\cdot |x_{1}-x_{2}|}$.

Das heißt, ${\displaystyle L}$ ist eine Lipschitzkonstante für diese Funktion auf dem Intervall ${\displaystyle \left[a,b\right]}$.

Weil für ${\displaystyle g}$ der Quotient gleich ${\displaystyle |x_{1}+x_{2}|}$ ist, folgt, dass ${\displaystyle g}$ nur für einen beschränkten Definitionsbereich lipschitzstetig ist, für einen unbeschränkten jedoch nicht. Die ebenfalls durch ${\displaystyle g(x)=x^{2}}$ definierte Funktion ${\displaystyle g\colon \mathbb {R} \to \mathbb {R} }$ ist deshalb nicht lipschitzstetig.

• Die Betragsfunktion ${\displaystyle h\colon \mathbb {R} \rightarrow \mathbb {R} }$, definiert als

${\displaystyle h(x)=|x|}$,

ist wegen der umgekehrten Dreiecksungleichung ${\displaystyle {\bigl |}|x_{1}|-|x_{2}|{\bigr |}\leq |x_{1}-x_{2}|}$ lipschitzstetig mit ${\displaystyle L=1}$, aber sie ist (an der Stelle ${\displaystyle x=0}$) nicht differenzierbar.

Anwendung

Lipschitzstetigkeit i​st ein wichtiges Konzept i​n der Theorie gewöhnlicher Differentialgleichungen, u​m Existenz u​nd Eindeutigkeit v​on Lösungen z​u beweisen (siehe Satz v​on Picard-Lindelöf). Selbstabbildungen m​it einer Lipschitzkonstante kleiner a​ls eins n​ennt man Kontraktionen. Diese s​ind wichtig für d​en Fixpunktsatz v​on Banach.

In d​er Theorie partieller Differentialgleichungen werden Lipschitz-Gebiete betrachtet. Diese h​aben die Eigenschaft, d​ass ihr Rand, d​er Lipschitz-Rand genannt wird, l​okal durch e​ine lipschitzstetige Funktion beschrieben werden kann.

Lipschitz-Raum

Ist ${\displaystyle X\subseteq \mathbb {R} }$ (oder allgemeiner ${\displaystyle \left(X,\,d_{X}\right)}$ ein metrischer Raum), so wird die Menge der reellwertigen lipschitzstetigen Funktionen auf ${\displaystyle X}$ gelegentlich mit ${\displaystyle \operatorname {Lip} \left(X\right)}$ bezeichnet.

Für ${\displaystyle X\subseteq \mathbb {R} }$ (oder allgemeiner für ${\displaystyle X\subseteq \mathbb {R} ^{n}}$ mit der euklidischen Metrik) ist jede affin-lineare Funktion lipschitzstetig. Auf einem allgemeinen metrischen Raum sind immerhin alle konstanten Funktionen lipschitzstetig. Insbesondere ist ${\displaystyle \operatorname {Lip} \left(X\right)}$ nicht leer und enthält die konstante Nullfunktion.

Sind ${\displaystyle f,\,g\in \operatorname {Lip} \left(X\right)}$ und ${\displaystyle \lambda \in \mathbb {R} }$, so gilt ${\displaystyle \lambda \,f\in \operatorname {Lip} \left(X\right)}$ sowie ${\displaystyle f+g\in \operatorname {Lip} \left(X\right)}$. Damit ist ${\displaystyle \operatorname {Lip} \left(X\right)}$ ein reeller Vektorraum, ein Funktionenraum.

Ist die Menge ${\displaystyle X}$ zudem noch beschränkt, so gilt außerdem für das punktweise Produkt ${\displaystyle f\cdot g\in \operatorname {Lip} \left(X\right)}$. Damit wird ${\displaystyle \operatorname {Lip} \left(X\right)}$ zu einer Funktionenalgebra.

Siehe auch

• Satz von Kirszbraun über die Fortsetzbarkeit lipschitzstetiger Funktionen
• Bilipschitz-Äquivalenz: Eine bijektive, lipschitzstetige Abbildung zwischen metrischen Räumen mit lipschitzstetigem Inversen.

Literatur

• Harro Heuser: Lehrbuch der Analysis – Teil 1, 6-te Auflage, Teubner 1989, ISBN 3-519-42221-2, S. 136, 212
• Konrad Königsberger: Analysis 1. 2-te Auflage, Springer 1992, ISBN 3-540-55116-6, S. 80
• Wolfgang Walter: Analysis 1. 7-te Auflage, Springer 2004, ISBN 978-3-540-35078-1, S. 44, 45

Weblinks

• Lipschitz condition in der Encyclopaedia of Mathematics (abgerufen 2. Dezember 2009)
• Lipschitz condition. In: PlanetMath. (englisch)

Einzelnachweise

1. Walter Rudin: Functional Analysis. McGraw-Hill, New York 1991. ISBN 0070542368, S. 41, 420.