Mathematikdidaktik

Mathematikdidaktik ist eine Fachdidaktik für das Fach Mathematik. Sie beschäftigt sich als Wissenschaft mit dem Lehren und Lernen von Mathematik[1] für alle Altersstufen und umfasst sowohl Lernziele, Inhalte und Lehrmethoden im Mathematikunterricht als auch das Lernverhalten von Schülern. Als Hochschuldisziplin wird Mathematikdidaktik an Pädagogischen Hochschulen und Universitäten gelehrt und ist integraler Bestandteil der Ausbildung für das Lehramt im Fach Mathematik.

Mathematikdidaktik im Kontext ihrer Einflussgrößen

Die internationale Gesellschaft für Mathematikdidaktik ist die 1908 gegründete International Commission on Mathematical Instruction (ICMI), die alle vier Jahre den International Congress on Mathematical Education (ICME) ausrichtet.

Entwicklung der Mathematikdidaktik

Geometrieunterricht, Illustration auf einer mittelalterlichen Ausgabe der Elemente des Euklid.

Die Anfänge der Mathematikdidaktik sind eng mit der Entwicklung der Mathematik und der jeweiligen Lehrpläne für das Fach verbunden.[2] Während sich in der Antike die Didaktik in Babylon und Ägypten überwiegend auf Elementarmathematik konzentrierte, verbanden insbesondere die Griechen Platon, Aristoteles und Euklid Mathematik mit philosophischen Fragestellungen. Letzterer schrieb eines der ersten mathematischen Lehrbücher, „Die Elemente“. Ab dem Mittelalter wurden mathematische Fächer wie Arithmetik und Geometrie im Rahmen des Quadrivium unterrichtet. Als erste didaktische Werke für einen Mathematikunterricht lassen sich die Rechenbücher von Adam Ries auffassen.[3] Mit der Zunahme der Bedeutung des Handels erhielt insbesondere das Rechnen und damit das Unterrichten von Mathematik eine wichtige gesellschaftliche Stellung. Lehrlinge von Ausbildungsberufen wie Maurer, Geldverleiher, Kaufleute erlernten berufsbezogene, mathematische Fähigkeiten. Zunächst bildeten sich historisch bedingt themenspezifische Fachdidaktiken heraus: Arithmetik, Geometrie, Trigonometrie, wobei ein fragend-entwickelnder Unterrichtsstil vorherrschte.[4]

Als Entwicklungs- und Forschungsgebiet ist die Mathematikdidaktik ein eher junges Gebiet.[5] Sie hat sich insbesondere seit dem 19. Jahrhundert entfaltet. Nachhaltig wurde sie durch das Humboldtsche Bildungsideal geprägt, was einhergeht mit der Durchsetzung eines allgemeinbildenden, staatlichen Schulsystems, der bildungspolitischen Konzeption des Neuhumanismus und dem Ziel einer Erziehung zur Selbständigkeit und zur Persönlichkeitsentfaltung. Die Trennung in verschiedene Schulzweige wie Volksschule und höhere Schule sowie die Geschlechtertrennung in Höhere Töchterschulen für Mädchen und Gymnasien für Jungen führte zur Herausbildung schwerpunktbezogener Mathematikdidaktiken, die besonders die jeweiligen soziokulturellen und anthropogenen Rahmenbedingungen (siehe Berliner Modell) berücksichtigten. Besonderen Einfluss hatten weiterhin die Diskussion um die Mengenlehre, die im Wesentlichen durch Georg Cantor begründet wurde, und die Einführung des dezimalen Maßsystems. Gegen Ende des 19. Jahrhunderts fand eine Wandlung von der allgemeinen, erfahrungsgestützten Mathematikdidaktik zu einer zunehmend empirischen Wissenschaft statt. Im Jahr 1893 wurde ein Lehrstuhl für Mathematikdidaktik an der Georg-August-Universität Göttingen errichtet. Als weiterer Meilenstein lässt sich die Meraner Konferenz im Jahr 1905 auffassen, bei der insbesondere Felix Klein Mathematikunterricht als eine wichtige Aufgabe der Erziehung zum funktionalen Denken hervorhob und sich für die Aufnahme von Analysis in den Lehrplan aussprach. Gleichzeitig begann eine intensive internationale Zusammenarbeit. 1908 wurde auf dem internationalen Kongress der Mathematiker in Rom die „Internationale Mathematische Kommission“ (IMUK) mit Klein als Vorsitzendem gegründet.[6][7][8]

In der Zeit des Nationalsozialismus wurden die Mathematik und damit ihre Didaktik nationalistischen, rassistischen und militärischen Zielen untergeordnet und im Zusammenhang mit Anwendungen der Aerostatik, Aerodynamik und Ballistik thematisiert. Vertreter einer solchen Fachdidaktik waren etwa Erich Günther[9] und Karl Hahn[10] (Beide übten als Pädagogen auch schulpolitischen Einfluss aus[11]). Nach dem Zweiten Weltkrieg beeinflusste insbesondere die Methodik von Walter Lietzmann die Mathematikdidaktik. In den 1950er-Jahren schlugen sich die Diskussionen um unterrichtliche Konzeptionen wie die eines handlungsorientiert-emanzipatorischen, genetischen, anwendungs- und problemorientierten Mathematikunterrichts in Arbeiten der Mathematikdidaktik nieder. Die in den siebziger Jahren aufkommende Neue Mathematik und die in den achtziger Jahren beginnende Technisierung beispielsweise durch die Einführung des Taschenrechners fand ebenfalls Einzug in diese Fachdidaktik. Letzteres wurde maßgeblich durch Hans-Georg Weigand geprägt.[12] Seitdem hat sich die Mathematikdidaktik weiter als Hochschuldisziplin etabliert und trägt maßgeblich zur Qualifikation von Mathematiklehrenden bei.[6] 1975 wurde auf dem 9. Bundeskongress der Mathematikdidaktik die „Gesellschaft für Didaktik der Mathematik“ (GDM) gegründet, die sich als wissenschaftliche Vereinigung mit dem Ziel versteht, die Didaktik der Mathematik – insbesondere in deutschsprachigen Ländern – zu fördern und mit entsprechenden Institutionen in anderen Ländern zusammenzuarbeiten.[13] 1975 fand auch der erste „Weltkongress der Mathematikdidaktik“ an der Universität Karlsruhe (ICDM) statt, der im Jahr 2016 erneut in Deutschland an der Universität Hamburg vorgesehen ist.[14] 1977 wurde die „Mathematik-Unterrichts-Einheiten-Datei“ (MUED), eine selbstverwaltete Organisation von Mathematiklehrerinnen und -lehrern aller Schularten mit der Idee ins Leben gerufen, anwendungsbezogenen Mathematikunterricht zu entwickeln, zu erproben und sich darüber auszutauschen.[15] Weiterhin hatten curriculare Entwicklungen wie die Reform der gymnasialen Oberstufe in den achtziger Jahren, die Saarbrücker Rahmenvereinbarung der Nachkriegsjahre, bei der bereits Mathematik als Pflichtfach aufgeführt war, sowie die 2003 von der deutschen Kultusministerkonferenz als Folge der PISA-Studie eingeführten Bildungsstandards Einfluss auf die Mathematikdidaktik.[16] Auch in anderen Ländern wie beispielsweise dem Vereinigten Königreich[17] und den Vereinigten Staaten[18] sind vergleichbare Standards definiert worden.

Neuere Forschungen auf dem Gebiet dieser Fachdidaktik knüpfen an theoretische Analysen sowie vorhandene, auf qualitativen und quantitativen Studien basierenden Forschungsergebnisse an und nutzen systematisch empirische Methoden, um offene theoretische Fragen zu klären. Die Forschungsprojekte sind sehr vielfältig.[19] Beispiele sind u. a. das Gebiet der „Mathematikdidaktik als design science“[20] und in kleinerem Rahmen die „Fehler-Didaktik“.[21][22]

Bezugswissenschaften

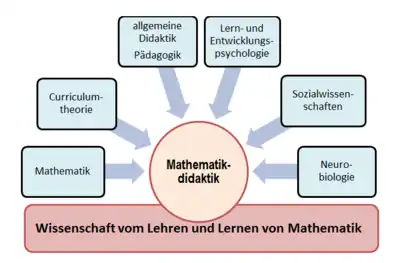
Die Mathematikdidaktik lässt sich nicht isoliert betrachten, sondern wendet Methoden und Resultate anderer wissenschaftlicher Disziplinen an oder berücksichtigt deren Erkenntnisse und Erfahrungen. Bezugswissenschaften sind als erstes die Mathematik selbst, die den Lerngegenstand stellt und weiterhin die Pädagogik, die Psychologie, die allgemeine Didaktik, die Sozialwissenschaften, die Neurobiologie, die Erkenntnistheorie und die Bildungsforschung.[23][24] Zusätzlich können im Bereich von Anwendungen beispielsweise Wissenschaften wie Kunst tangiert werden.[25]

Aufgabenbereiche

Heinz Griesel (1931–2018) definiert Mathematikdidaktik als[26]

„Wissenschaft von der Entwicklung praktikabler Kurse für das Lernen im Bereich der Mathematik sowie der praktischen und empirischen Überprüfung der Kurse einschließlich der Überlegungen zur Zielsetzung der Kurse und der Stoffauswahl.“

Die wesentliche Aufgabe der Mathematikdidaktik besteht darin, Lehren und Lernen von Mathematik hinsichtlich seiner Ziele, Bedingungen und Methoden zu erforschen und zu verbessern. Sie besitzt demnach sowohl einen normativen, als auch deskriptiven und empirischen Charakter. Traditionell vorherrschender Teil ist die Organisation von Lernprozessen im Mathematikunterricht als Praxisaufgabe für Kinder (Grundschule) und Jugendliche (Sekundarstufen bis zum Abitur). Die Mathematikdidaktik formuliert präskriptiv Aussagen darüber, welche Inhalte und Unterrichtsmethoden effektiv und sinnvoll sind, konstruiert und entwickelt u. a. Curricula, Lehrverfahren, Lernmaterialien und verbindet und systematisiert integrativ verschiedene Dimensionen des Handlungsfeldes von Mathematiklehrkräften.[27] Dieser Sicht folgend lässt sich die Mathematikdidaktik als „Berufsdisziplin des Mathematiklehrers“[28] auffassen, die im Rahmen der Hochschulausbildung und durch Fortbildungs- bzw. Weiterbildungsangebote erarbeitet wird. Als freier Träger ist beispielsweise bundesweit das Projekt „Teachers Teaching with Technology Deutschland“ (kurz: T³ Deutschland) tätig.

Neben Forschungsarbeiten für den Bereich der allgemeinbildenden Schulen gibt es weitere berufsbezogene Aufgabenfelder wie Berufsausbildung, Studium an Hochschulen, Erwachsenenbildung, bei denen spezielle fachdidaktische Aspekte einfließen können. Außerdem existieren neben der allgemeinen Fachdidaktik spezielle didaktische Überlegungen zu bestimmten Zielgruppen wie beispielsweise Grundschülern oder Teilgebieten der Mathematik wie Didaktik der Analysis,[29] der Geometrie,[30] der Algebra,[31] der Arithmetik[32] oder der Stochastik.[33]

Didaktische Prinzipien

Die Mathematikdidaktik lässt sich bezogen auf ihren Lerninhalt, die Mathematik, als übergeordnet auffassen, da sie über Erkenntnisweisen des Fachs nachdenkt[34] und didaktische Prinzipien in ihre Überlegungen einbezieht. Letztere stellen die Unterrichtsmethodik als Teilgebiet der Fachdidaktik in den Mittelpunkt, anhand derer Mathematikunterricht geplant und beurteilt werden kann. Didaktische Prinzipien besitzen einen normativen Charakter. Sie sind zunächst nicht unbedingt mathematikspezifisch, aber einige Prinzipien haben eine besondere Bedeutung für das Lehren und Lernen der Mathematik.[35] Hier ist anzumerken, dass für die normativen Aussagen gesellschaftliche Bezugspunkte benötigt werden und die Entscheidung über die Lerninhalte sowie die Ziele von Bildung und Erziehung als politisch-rechtlich determiniert zu begreifen ist.[36] In der mathematikdidaktischen Literatur sind eine Reihe von Prinzipien zu finden.[37] Als grundlegend gelten das Spiralprinzip, das auf Jerome Bruner zurückgeht, das genetische Prinzip nach Martin Wagenschein und das operative Prinzip, das von Jean Piaget und seinem Schüler Hans Aebli postuliert wurde. Hieraus lassen sich weitere methodische Konzeptionen wie der handlungsorientierte, der anwendungsorientierte oder auch der problemorientierte Unterricht ableiten.[38]

Konsequenzen für den Mathematikunterricht

Die Frage nach der Legitimation ist eine der wichtigsten Fragestellungen, die sich die Mathematikdidaktik stellen muss, nämlich, inwieweit Mathematikunterricht überhaupt notwendig ist und mit welchen Argumenten diese Notwendigkeit begründet werden kann. Gesucht wird nach einer Antwort darauf, ob Mathematikunterricht für den Einzelnen und die Gesellschaft wirklich so wichtig ist, dass jeder Schüler verbindlich daran teilnehmen muss.[39] Hans Werner Heymann beantwortet dies durch eine Orientierung an der Allgemeinbildung als Teil des Allgemeinwissens.[40] Schon laut Piaget dient Mathematik als Instrument zur Erforschung kindlicher Denkvorgänge und der psychischen und intellektuellen Fähigkeiten von Kindern.[41] Die Beschäftigung mit Mathematik kann Schülern schon früh die Möglichkeit geben, Erfahrungen mit wissenschaftlichen – im Sinne von wissenschaftspropädeutischen – Arbeitsweisen zu machen und sich mit einer mathematischen Beschreibung der Wirklichkeit auseinanderzusetzen.[42]

Die in den Curricula 2003 formulierten nationalen Bildungsstandards Mathematik zielen auf eine Überprüfbarmachung und damit Standardisierung mathematischen Wissens ab. Sie sind als Leistungsstandards, nicht aber als Unterrichtsstandards aufzufassen und sollen bewusst kreative Freiräume zulassen.[43]

Im Rahmen der Auseinandersetzung der Mathematikdidaktik mit der Thematik, wie Mathematikunterricht an den Schulen und Hochschulen besser vermittelt werden kann, gesellt sich gerade in Deutschland im Gegensatz zu Ländern wie Frankreich die Fragestellung, wieso immer weniger Personen den Beruf des Mathematikers trotz guter Berufsaussichten ergreifen wollen und trotz des Anwendungsbezugs anscheinend ein gesellschaftlich sogar anerkanntes Desinteresse an der Mathematik vorherrscht.[44] Eine wesentliche Rolle im Mathematikunterricht spielen die Aufgaben.[45] Im Rahmen einer Aufgabendidaktik nennt beispielsweise Timo Leuders folgende Dimensionen von Aufgabenqualität: Authentizität, Bedeutsamkeit, Relevanz, Offenheit und Aufforderungscharakter.[46] Weitere entscheidende Einflussgröße auf die Leistung der Schüler und ihre emotionale Beziehung zur Mathematik ist die unterrichtende Lehrkraft, deren didaktische Kompetenz in folgender Aussage zusammengefasst wird: „Ein guter Mathematiklehrer ist ein Lehrer, der sein Wissen und seine Liebe zur Mathematik an seine Schüler weitergibt, sodass auch die Schüler die Auseinandersetzung mit Mathematik genießen können.“[47] Die Erforschung von subjektiven Theorien und Handlungsmustern von Mathematiklehrern ist ebenfalls ein Forschungsgebiet der Mathematikdidaktik.[48][49]

Literatur

Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4.
Timo Leuders (Hrsg.): Mathematik-Didaktik. Cornelsen Scriptor, Berlin 2007, ISBN 978-3-589-21695-6.
Hans-Georg Steiner (Hrsg.): Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-06005-9.
Friedrich Zech: Grundkurs Mathematikdidaktik. Theoretische und praktische Anleitungen für das Lehren und Lernen von Mathematik. Beltz, Weinheim/Basel 2002, ISBN 3-407-25216-1.
Helge Lenné: Analyse der Mathematikdidaktik in Deutschland. Aus dem Nachlass herausgegeben von Walter Jung, Klett 1969, 2. Auflage 1975 (Geschichte der Mathematikdidaktik in Deutschland bis 1969)

Weblinks

Commons: Mathematikdidaktik – Sammlung von Bildern, Videos und Audiodateien

Website der Gesellschaft für Didaktik der Mathematik
Website des Vereins zur Förderung des mathematischen und naturwissenschaftlichen Unterrichts e. V.
Madipedia Nachschlagewerk für Mathematikdidaktik, mit weiteren Links auf Arbeitskreise, Zeitschriften, Personen, Forschungsarbeiten
Didaktik der Mathematik Zum-Wiki
Didaktik der Mathematik, Lehrpläne, Links zu Instituten für die Didaktik der Mathematik, wichtigen Institutionen und Vereinen sowie zur Lehrplan-Datenbank der Kultusministerkonferenz Lehrer-Online

Einzelnachweise

Bernd Hafenbrak: Einführung in die Mathematikdidaktik: Einleitung. (PDF; 19 kB) (Nicht mehr online verfügbar.) Archiviert vom Original am 4. März 2016; abgerufen am 1. November 2015.
Marco Drönner: Die geschichtliche Entwicklung der Mathematikdidaktik mit dem Fokus auf die Beeinflussung der Didaktik durch das Humboldtsche Bildungsideal, der Meraner Reform und der neuen Mathematik. GRIN Verlag, München 2012, ISBN 978-3-656-25915-2, S. 1.
Marco Drönner: Die geschichtliche Entwicklung der Mathematikdidaktik mit dem Fokus auf die Beeinflussung der Didaktik durch das Humboldtsche Bildungsideal, der Meraner Reform und der neuen Mathematik. GRIN Verlag, München 2012, ISBN 978-3-656-25915-2, S. 2 f.
Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4, S. 5–7.
Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4, S. 2.
Universität Bielefeld: Ludger Huster: Dokumentation zur Entwicklung der Mathematik-Didaktik im 19. Jahrhundert: Elementarschulbereich. Bielefeld 1981, S. 9–13.
Hans-Georg Steiner (Hrsg.): Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-06005-9, S. 9–21.
Marco Drönner: Die geschichtliche Entwicklung der Mathematikdidaktik mit dem Fokus auf die Beeinflussung der Didaktik durch das Humboldtsche Bildungsideal, der Meraner Reform und der neuen Mathematik. GRIN Verlag, München 2012, ISBN 978-3-656-25915-2, S. 1–5.
Erich Günther: Handbuch der Wehrphysik. Frankfurt am Main 1936.
Karl Hahn: [Referat über den Physikuntericht]. In: 25 Jahre Meraner Reform und die heutige Lage des mathematischen und naturwissenschaftlichen Unterrichts. In: Unterrichtsblätter für Mathematik und Naturwissenschaften. Band 17, 1931, S. 162–169.
Jörg Willer: Fachdidaktik im Dritten Reich am Beispiel der Physik. In: Medizinhistorische Mitteilungen. Zeitschrift für Wissenschaftsgeschichte und Fachprosaforschung. Band 34, 2015, ISBN 978-3-86888-118-9, S. 105–121, passim.
Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4, S. 2–11.
Über die GDM. Abgerufen am 6. Juli 2013.
Weltkongress der Mathematikdidaktik. (Nicht mehr online verfügbar.) Ehemals im Original; abgerufen am 8. Juli 2013.@1@2 (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.
Die MUED: Was wir sind – was wir wollen. Abgerufen am 7. Juli 2013.
Kolloquium Mathematik und ihre Didaktik – SS 2013. (Nicht mehr online verfügbar.) Archiviert vom Original am 21. August 2011; abgerufen am 9. Juli 2013. Kolloquium Mathematik und ihre Didaktik – SS 2013 (Memento vom 21. August 2011 im Internet Archive)
The school curriculum. Abgerufen am 9. Juli 2013 (englisch).
Principles and Standards for School Mathematics. Abgerufen am 7. Juli 2013 (englisch).
Kategorie:Forschungsprojekte. Abgerufen am 7. Juli 2013.
Christoph Selter, Gerd Walther (Hrsg.): Mathematikdidaktik als design science. Klett Grundschulverlag, Leipzig 1999, ISBN 3-12-200060-1.
Lernen aus Fehlern im Mathematikunterricht. Abgerufen am 9. Juli 2013.
Reinhard Kahl: Lehrer als Feinde. Die Zeit 28/2007, abgerufen am 9. Juli 2013.
Katja Maaß: Spannungsfeld zwischen Fachwissenschaft und Fachdidaktik. S. 28, abgerufen am 21. Mai 2013.
Timo Leuders: Mathematik Didaktik. Cornelsen Verlag, Berlin 2003, ISBN 3-589-21695-6, S. 11.
Alfred Schreiber: Grundzüge der Mathematikdidaktik. Abgerufen am 11. Mai 2013.
Heinz Griesel: Die Neue Mathematik für Lehrer und Studenten: Band 1. Schrödel Verlag, Hannover 1971, S. 296.
Erich Wittmann: Grundfragen des Mathematikunterrichts. 6. Auflage. Vieweg Verlag, Braunschweig 1981, S. 2.
Alfred Schreiber: Grundzüge der Mathematikdidaktik. Abgerufen am 11. Mai 2013.
Werner Blum, Günter Törner: Didaktik der Analysis. Vandenhoeck & Ruprecht, Göttingen 1983, ISBN 3-525-40545-6.
Hans Georg Weigand u. a.: Didaktik der Geometrie für die Sekundarstufe I. Spektrum Verlag, Heidelberg 2009, ISBN 978-3-8274-1715-2.
Hans Georg Weigand, Hans Joachim Vollrath: Algebra in der Sekundarstufe. 3. Auflage. Spektrum Verlag, Heidelberg 2007, ISBN 978-3-8274-1803-6.
Friedhelm Padberg: Didaktik der Arithmetik für Lehrerausbildung und Fortbildung. Elsevier-Spektrum, Heidelberg 2009, ISBN 978-3-8274-0993-5.
Herbert Kütting: Didaktik der Stochastik. BI Wissenschaftsverlag, Mannheim 1994, ISBN 3-411-16831-5.
Alfred Schreiber: Grundzüge der Mathematikdidaktik. Abgerufen am 11. Mai 2013.
Werner Blum, Günter Törner: Didaktik der Analysis. Vandenhoeck & Ruprecht, Göttingen 1983, ISBN 3-525-40545-6, S. 238–239.
Timo Leuders: Mathematik Didaktik. Cornelsen Verlag, Berlin 2003, ISBN 3-589-21695-6, S. 11.
Hans Georg Weigand: Didaktische Prinzipien. (PDF; 182 kB) S. 1, abgerufen am 10. Juli 2013.
Friedrich Zech: Grundkurs Mathematikdidaktik. Theoretische und praktische Anleitungen für das Lehren und Lernen von Mathematik. Beltz, Weinheim/Basel 2002, ISBN 3-407-25216-1, S. 112–117.
Hans-Georg Bigalke: Sinn und Bedeutung der Mathematikdidaktik. In: Hans-Georg Steiner (Hrsg.). Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-06005-9, S. 115.
Hans Werner Heymann: Allgemeinbildung als Aufgabe der Schule und als Maßstab für Fachunterricht. (PDF; 60 kB) (Nicht mehr online verfügbar.) Archiviert vom Original am 24. Dezember 2012; abgerufen am 10. Juli 2013. Allgemeinbildung als Aufgabe der Schule und als Maßstab für Fachunterricht (Memento vom 24. Dezember 2012 im Internet Archive)
Emma Castelnuovo: Didaktik der Mathematik. Akademische Verlagsgesellschaft, Frankfurt/Main 1968, S. 176–177.
Horst Jahner: Methodik des mathematischen Unterrichts. 6. Auflage. Quelle und Meyer Verlag, Heidelberg/Wiesbaden 1985, ISBN 3-494-00977-5, S. 10–11.
Werner Blum u. a.: Bildungsstandards Mathematik: konkret. 5. Auflage. Cornelsen Scriptor, Berlin 2011, ISBN 978-3-589-22321-3, S. 15.
Mathephobie ist ein deutsches Phänomen. In: Berliner Zeitung. 28. März 2007, abgerufen am 10. Juli 2013.
Timo Leuders: Qualität im Mathematikunterricht der Sekundarstufe 1 und 2. Cornelsen Scriptor, Berlin 2001, ISBN 3-589-21425-2, S. 94.
Timo Leuders: Qualität im Mathematikunterricht der Sekundarstufe 1 und 2. Cornelsen Scriptor, Berlin 2001, ISBN 3-589-21425-2, S. 99.
Karl Hehl: Warum Mathematik. (PDF; 104 kB) (Nicht mehr online verfügbar.) S. 2, archiviert vom Original am 4. März 2016; abgerufen am 10. Juli 2013.
Berufsbezogene Kognitionen, Einstellungen und subjektive Theorien von Mathematiklehrern. Abgerufen am 10. Juli 2013.
Handlungsmuster von Lehrerinnen und Lehrern beim Einsatz neuer Medien in den Fächern Deutsch, Mathematik und Informatik. Abgerufen am 10. Juli 2013.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bernd Hafenbrak: Einführung in die Mathematikdidaktik: Einleitung. (PDF; 19 kB) (Nicht mehr online verfügbar.) Archiviert vom Original am 4. März 2016; abgerufen am 1. November 2015.

[2] Marco Drönner: Die geschichtliche Entwicklung der Mathematikdidaktik mit dem Fokus auf die Beeinflussung der Didaktik durch das Humboldtsche Bildungsideal, der Meraner Reform und der neuen Mathematik. GRIN Verlag, München 2012, ISBN 978-3-656-25915-2, S. 1.

[3] Marco Drönner: Die geschichtliche Entwicklung der Mathematikdidaktik mit dem Fokus auf die Beeinflussung der Didaktik durch das Humboldtsche Bildungsideal, der Meraner Reform und der neuen Mathematik. GRIN Verlag, München 2012, ISBN 978-3-656-25915-2, S. 2 f.

[4] Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4, S. 5–7.

[5] Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4, S. 2.

[Huster-6] Universität Bielefeld: Ludger Huster: Dokumentation zur Entwicklung der Mathematik-Didaktik im 19. Jahrhundert: Elementarschulbereich. Bielefeld 1981, S. 9–13.

[7] Hans-Georg Steiner (Hrsg.): Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-06005-9, S. 9–21.

[8] Marco Drönner: Die geschichtliche Entwicklung der Mathematikdidaktik mit dem Fokus auf die Beeinflussung der Didaktik durch das Humboldtsche Bildungsideal, der Meraner Reform und der neuen Mathematik. GRIN Verlag, München 2012, ISBN 978-3-656-25915-2, S. 1–5.

[9] Erich Günther: Handbuch der Wehrphysik. Frankfurt am Main 1936.

[10] Karl Hahn: [Referat über den Physikuntericht]. In: 25 Jahre Meraner Reform und die heutige Lage des mathematischen und naturwissenschaftlichen Unterrichts. In: Unterrichtsblätter für Mathematik und Naturwissenschaften. Band 17, 1931, S. 162–169.

[11] Jörg Willer: Fachdidaktik im Dritten Reich am Beispiel der Physik. In: Medizinhistorische Mitteilungen. Zeitschrift für Wissenschaftsgeschichte und Fachprosaforschung. Band 34, 2015, ISBN 978-3-86888-118-9, S. 105–121, passim.

[12] Heinz Jörg Claus: Einführung in die Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1989, ISBN 3-534-08736-4, S. 2–11.

[13] Über die GDM. Abgerufen am 6. Juli 2013.

[14] Weltkongress der Mathematikdidaktik. (Nicht mehr online verfügbar.) Ehemals im Original; abgerufen am 8. Juli 2013.@1@2 (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.

[15] Die MUED: Was wir sind – was wir wollen. Abgerufen am 7. Juli 2013.

[16] Kolloquium Mathematik und ihre Didaktik – SS 2013. (Nicht mehr online verfügbar.) Archiviert vom Original am 21. August 2011; abgerufen am 9. Juli 2013. Kolloquium Mathematik und ihre Didaktik – SS 2013 (Memento vom 21. August 2011 im Internet Archive)

[17] The school curriculum. Abgerufen am 9. Juli 2013 (englisch).

[18] Principles and Standards for School Mathematics. Abgerufen am 7. Juli 2013 (englisch).

[19] Kategorie:Forschungsprojekte. Abgerufen am 7. Juli 2013.

[20] Christoph Selter, Gerd Walther (Hrsg.): Mathematikdidaktik als design science. Klett Grundschulverlag, Leipzig 1999, ISBN 3-12-200060-1.

[21] Lernen aus Fehlern im Mathematikunterricht. Abgerufen am 9. Juli 2013.

[22] Reinhard Kahl: Lehrer als Feinde. Die Zeit 28/2007, abgerufen am 9. Juli 2013.

[23] Katja Maaß: Spannungsfeld zwischen Fachwissenschaft und Fachdidaktik. S. 28, abgerufen am 21. Mai 2013.

[24] Timo Leuders: Mathematik Didaktik. Cornelsen Verlag, Berlin 2003, ISBN 3-589-21695-6, S. 11.

[25] Alfred Schreiber: Grundzüge der Mathematikdidaktik. Abgerufen am 11. Mai 2013.

[26] Heinz Griesel: Die Neue Mathematik für Lehrer und Studenten: Band 1. Schrödel Verlag, Hannover 1971, S. 296.

[27] Erich Wittmann: Grundfragen des Mathematikunterrichts. 6. Auflage. Vieweg Verlag, Braunschweig 1981, S. 2.

[28] Alfred Schreiber: Grundzüge der Mathematikdidaktik. Abgerufen am 11. Mai 2013.

[29] Werner Blum, Günter Törner: Didaktik der Analysis. Vandenhoeck & Ruprecht, Göttingen 1983, ISBN 3-525-40545-6.

[30] Hans Georg Weigand u. a.: Didaktik der Geometrie für die Sekundarstufe I. Spektrum Verlag, Heidelberg 2009, ISBN 978-3-8274-1715-2.

[31] Hans Georg Weigand, Hans Joachim Vollrath: Algebra in der Sekundarstufe. 3. Auflage. Spektrum Verlag, Heidelberg 2007, ISBN 978-3-8274-1803-6.

[32] Friedhelm Padberg: Didaktik der Arithmetik für Lehrerausbildung und Fortbildung. Elsevier-Spektrum, Heidelberg 2009, ISBN 978-3-8274-0993-5.

[33] Herbert Kütting: Didaktik der Stochastik. BI Wissenschaftsverlag, Mannheim 1994, ISBN 3-411-16831-5.

[34] Alfred Schreiber: Grundzüge der Mathematikdidaktik. Abgerufen am 11. Mai 2013.

[35] Werner Blum, Günter Törner: Didaktik der Analysis. Vandenhoeck & Ruprecht, Göttingen 1983, ISBN 3-525-40545-6, S. 238–239.

[36] Timo Leuders: Mathematik Didaktik. Cornelsen Verlag, Berlin 2003, ISBN 3-589-21695-6, S. 11.

[37] Hans Georg Weigand: Didaktische Prinzipien. (PDF; 182 kB) S. 1, abgerufen am 10. Juli 2013.

[38] Friedrich Zech: Grundkurs Mathematikdidaktik. Theoretische und praktische Anleitungen für das Lehren und Lernen von Mathematik. Beltz, Weinheim/Basel 2002, ISBN 3-407-25216-1, S. 112–117.

[39] Hans-Georg Bigalke: Sinn und Bedeutung der Mathematikdidaktik. In: Hans-Georg Steiner (Hrsg.). Didaktik der Mathematik. Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-06005-9, S. 115.

[40] Hans Werner Heymann: Allgemeinbildung als Aufgabe der Schule und als Maßstab für Fachunterricht. (PDF; 60 kB) (Nicht mehr online verfügbar.) Archiviert vom Original am 24. Dezember 2012; abgerufen am 10. Juli 2013. Allgemeinbildung als Aufgabe der Schule und als Maßstab für Fachunterricht (Memento vom 24. Dezember 2012 im Internet Archive)

[41] Emma Castelnuovo: Didaktik der Mathematik. Akademische Verlagsgesellschaft, Frankfurt/Main 1968, S. 176–177.

[42] Horst Jahner: Methodik des mathematischen Unterrichts. 6. Auflage. Quelle und Meyer Verlag, Heidelberg/Wiesbaden 1985, ISBN 3-494-00977-5, S. 10–11.

[43] Werner Blum u. a.: Bildungsstandards Mathematik: konkret. 5. Auflage. Cornelsen Scriptor, Berlin 2011, ISBN 978-3-589-22321-3, S. 15.

[44] Mathephobie ist ein deutsches Phänomen. In: Berliner Zeitung. 28. März 2007, abgerufen am 10. Juli 2013.

[45] Timo Leuders: Qualität im Mathematikunterricht der Sekundarstufe 1 und 2. Cornelsen Scriptor, Berlin 2001, ISBN 3-589-21425-2, S. 94.

[46] Timo Leuders: Qualität im Mathematikunterricht der Sekundarstufe 1 und 2. Cornelsen Scriptor, Berlin 2001, ISBN 3-589-21425-2, S. 99.

[47] Karl Hehl: Warum Mathematik. (PDF; 104 kB) (Nicht mehr online verfügbar.) S. 2, archiviert vom Original am 4. März 2016; abgerufen am 10. Juli 2013.

[48] Berufsbezogene Kognitionen, Einstellungen und subjektive Theorien von Mathematiklehrern. Abgerufen am 10. Juli 2013.

[49] Handlungsmuster von Lehrerinnen und Lehrern beim Einsatz neuer Medien in den Fächern Deutsch, Mathematik und Informatik. Abgerufen am 10. Juli 2013.