Tomahawk (Zeichengerät)

Der Tomahawk ist ein geometrisches „Werkzeug“, das aus einem Halbkreis und zwei Geradenabschnitten besteht. Die Grundform kann mit Zirkel und Lineal konstruiert werden. Mit einem Tomahawk kann man einen Winkel dreiteilen. Dies widerspricht nicht der Unlösbarkeit des klassischen Problems, da die erforderliche Verschiebung und Drehung des konstruierten Tomahawks in die nötige Lage über die dort erlaubten Konstruktionsmethoden hinausgeht.

Tomahawk

Winkeldreiteilung

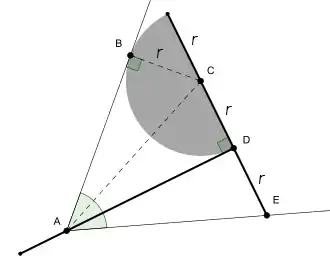
Dreiteilung eines Winkels mit einem Tomahawk

Man platziert den Tomahawk zu einem gegebenen Winkel so, dass sein Stiel durch die Spitze des Winkels läuft, seine Klinge den einen Schenkel des Winkels berührt und sein hinteres Ende den anderen Schenkel. Nun bildet der Stiel mit den beiden Schenkeln zwei Winkel, deren Maß ein Drittel beziehungsweise zwei Drittel des Ausgangswinkels beträgt.

Aufgrund der Konstruktion des Tomahawk sind die Strecken CD und DE gleich lang und die Winkel ADC und ADE sind rechte Winkel. Nach dem Kongruenzsatz SWS sind damit die Dreiecke ADC und ADE kongruent. Weiterhin ist auch das Dreieck ABC zu diesen beiden kongruent, da es in B einen rechten Winkel (Kreistangente und Radius) besitzt, die Seitenlängen von BC und CD übereinstimmen (Radius) und es mit dem Dreieck ADC die Seite AC gemeinsam hat. Wegen der Kongruenz der drei Dreiecke sind die drei Winkel BAC, CAD und DAE gleich groß und teilen somit den gegebenen Winkel BAE in drei gleich große Teile.[1]

Geschichte

Es ist nicht gesichert, wer den Tomahawk erfunden hat. Die frühesten bekannten Erwähnungen stammen aus dem 19. Jahrhundert in Frankreich. Dort wird er in dem 1835 erschienenen Buch Géométrie appliquée a l'industrie, a l'usage des artistes et des ouvriers von Claude Lucien Bergery erwähnt.[2] Henri Brocard beschrieb ihn 1877 in einer Publikation, in der er die Entdeckung dem Marineoffizier Pierre-Joseph Glotin zuschrieb, der ihn 1863 in einem Aufsatz für die Mémoires de la Société des sciences physiques et naturelles de Bordeaux behandelt hatte.[3][4][5]

Weblinks

Commons: Tomahawk (geometry) – Sammlung von Bildern, Videos und Audiodateien

MathWorld/Wolfram (englisch)
Angle Trisection Problem: Trisect An Angle With a Tomahawk (englisch)

Einzelnachweise

C. Stanley Olgivy: Excursions in Geometry. Dover 1990, ISBN 0-486-26530-7, S. 139-140.
Yates, Robert C. "The Trisection Problem" S. 37 Fig. 21, THE FRANKLIN PRESS, INC. BATON ROUGE, LA 1942, 68 Seiten, abgerufen am 3. Dezember 2015.
Underwood Dudley: The Trisectors. 2. Auflage. MAA Spectrum, 1994, ISBN 0-88385-514-3, S. 14–16 (Anmerkung: Dudley schreibt fälschlicherweise Bricard statt Brocard und Glatin statt Glotin).
Henri Brocard: Note sur la division mécanique de l'angle. In: Bulletin de la Société Mathématique de France. 5 (1877), S. 43–47.
M. Glotin: De quelques moyens pratiques de diviser les angles en parties égales. In: Mémoires de la Société des Sciences physiques et naturelles de Bordeaux. Band 2, S. 253–278.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] C. Stanley Olgivy: Excursions in Geometry. Dover 1990, ISBN 0-486-26530-7, S. 139-140.

[2] Yates, Robert C. "The Trisection Problem" S. 37 Fig. 21, THE FRANKLIN PRESS, INC. BATON ROUGE, LA 1942, 68 Seiten, abgerufen am 3. Dezember 2015.

[3] Underwood Dudley: The Trisectors. 2. Auflage. MAA Spectrum, 1994, ISBN 0-88385-514-3, S. 14–16 (Anmerkung: Dudley schreibt fälschlicherweise Bricard statt Brocard und Glatin statt Glotin).

[4] Henri Brocard: Note sur la division mécanique de l'angle. In: Bulletin de la Société Mathématique de France. 5 (1877), S. 43–47.

[5] M. Glotin: De quelques moyens pratiques de diviser les angles en parties égales. In: Mémoires de la Société des Sciences physiques et naturelles de Bordeaux. Band 2, S. 253–278.