Kapitalwert

Der Kapitalwert (englisch net present value, NPV; auch Nettobarwert) ist eine betriebswirtschaftliche Kennzahl der dynamischen Investitionsrechnung. Der Kapitalwert ergibt sich aus der Summe der auf die Gegenwart abgezinsten zukünftigen Erfolge einer Investition. Durch die Abzinsung von zukünftigen Erfolgen auf die Gegenwart wird der Zeitwert des Geldes berücksichtigt: Je eher man über Geld verfügen kann, desto mehr Wert besitzt es. Durch die Abzinsung von Erfolgen auf einen einheitlichen Zeitpunkt können auch Zahlungen vergleichbar gemacht werden, die zu unterschiedlichen Zeitpunkten anfallen.

Abgrenzungen

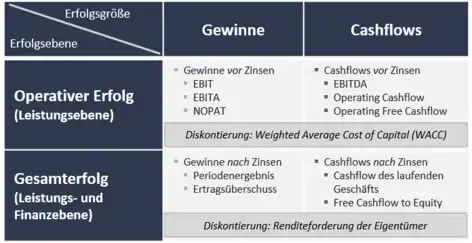
Erfolgsgrößen bei der Ermittlung von Kapitalwerten

Mithilfe von Kapitalwerten werden regelmäßig die aktuellen Werte von Sachanlagen (Grundstücken, Gebäuden, Maschinen etc.), Finanzanlagen (Aktien, Anleihen, Beteiligungen etc.) oder gar von ganzen Unternehmen ermittelt. Aufgrund von unterschiedlichen Berechnungen und Abgrenzungen der zukünftigen Erfolge gibt es sehr viele Varianten für die Berechnung von Kapitalwerten. International üblich bei der Bewertung von Investitionen ist heute die Kapitalisierung (Abzinsung) von Einzahlungsüberschüssen (Cashflows). Cashflows spiegeln häufig realistischer als Gewinne die Wertschaffung des betrachteten Vermögens wider. Die berechneten/ausgewiesenen Gewinne werden regelmäßig durch Spielräume bei der Bilanzierung (z. B. bei Berechnungen der Abschreibungen, Bemessung der Rückstellungen etc.) verzerrt. In der Bewertungspraxis hat sich durchgesetzt, sog. operative Gewinne oder Cashflows zu bewerten, die nicht durch finanzielle Aktivitäten überlagert werden. Es handelt sich hierbei um Erfolgsgrößen vor Zinszahlungen (genauer vor Finanzergebnissen). Die Betrachtung der operativen Ebene hat den Vorteil, dass sich die zukünftigen Erfolge schlüssig aus einer Analyse von Markt, Unternehmen und Wettbewerb prognostizieren lassen. Die mit der Finanzierung des Vermögens verbundenen Finanzierungsvorgänge und Zinszahlungen werden in den operativen Erfolgsgrößen nicht erfasst. Aufgrund von kaum vorhersehbaren Entwicklungen am Finanzmarkt sind zukünftige Zinszahlungen und Finanzströme regelmäßig schwer zu prognostizieren.

Mit der Abgrenzung der Erfolgsgröße korrespondiert die Auswahl des geeigneten Diskontierungszinses. Operative Ergebnisse bzw. operative Cashflows schaffen Werte für alle Kapitalgeber (Eigentümer und Fremdkapitalgeber) und müssen demzufolge mit der Renditeforderung aller Kapitalgeber abgezinst werden. Diesen Mischzinsfuß bezeichnet man auch als Weighted Average Cost of Capital (WACC). Werden dagegen Erfolgsgrößen nach Zinszahlungen betrachtet (die Ansprüche der Fremdkapitalgeber sind dann schon abgegolten), müssen die zukünftigen Erfolge nur noch mit der Renditeforderung der Eigentümer abgezinst werden. Die Bestimmung der Renditeforderungen der Eigenkapitalgeber fußt in der Regel auf kapitalmarkttheoretischen Modellen, zumeist wird auf das Capital Asset Pricing Model (CAPM) zurückgegriffen.

Für eine Beurteilung, ob sich eine Investition in die oben genannten Vermögensgegenstände lohnt, muss der Kapitalwert dem Wert der zu Beginn erforderlichen Investitionsauszahlung gegenübergestellt werden. Die Differenz zwischen dem Kapitalwert der zukünftigen Cashflows und dem aktuellen Wert der Investitionsauszahlung einer Investition bezeichnet man auch als Nettokapitalwert. Der Nettokapitalwert einer Investition entspricht dann der Summe der Barwerte aller mit der Investition verbundenen Zahlungen (Ein- und Auszahlungen). Bei den Investitionsauszahlungen handelt es sich häufig um aktuelle Marktpreise. Insofern vergleicht der Nettokapitalwert regelmäßig die Werte mit den Preisen von Investitionen. Eine Investition lohnt sich immer dann, wenn der Nettokapitalwert größer als null ist bzw. der (Kapital-)Wert der Investition seinen Preis übersteigt.

Beispiele: Der Kapitalwert von Unternehmen ergibt sich aus den abgezinsten/kapitalisierten Free Cashflows des Unternehmens. Der Kauf des ganzen Unternehmens lohnt sich, falls der Kapitalwert den aktuellen Börsenpreis (Enterprise Value) übersteigt. Den Wert einer Anleihe berechnet sich aus dem Kapitalwert aller in der Zukunft erwarteten Zahlungen (also Kuponzahlungen und Nennwertrückzahlung). Investitionen in eine Anleihe machen Sinn, falls der Kapitalwert den aktuell geforderten Preis an der Börse übersteigt. Der Wert von Immobilien errechnet sich aus den abgezinsten zukünftigen Erträgen aus der Immobilie. Eine Investition in die Immobilie würde sich lohnen, wenn ein Kaufpreis ausgehandelt werden kann, der unterhalb des Kapitalwertes der Immobilie liegt.

Die Nettokapitalwertmethode (auch NPV-Methode bzw. Net-Present-Value-Methode oder NGW-Methode)[1] erlaubt bei Unternehmen die Beurteilung von Erweiterungsinvestitionen und die Bestimmung des optimalen Ersatzzeitpunktes.

Berechnung

Berechnung von (Netto-)Kapitalwerten

Der Nettokapitalwert einer Investition berechnet sich formal wie folgt:

C_{0}(i)=-I+\sum _{t=1}^{T}{\frac {Z_{t}}{\left(1+i\right)^{t}}}+L\cdot \left(1+i\right)^{-T}=\sum _{t=0}^{T}\left(1+i\right)^{-t}\cdot Z'_{t}

$C_{0}$ : Nettokapitalwert bezogen auf den Zeitpunkt $t=0$
$i$ : Kalkulationszinssatz
$Z_{t}$ : Zahlungsstrom (Cashflow) in Periode $t$ , wobei $Z_{t}=E_{t}-A_{t}$ (Einzahlungen − Auszahlungen in Periode $t$ ) darstellt, bzw. $Z'_{t}$ ganz allgemein für einen Zahlungsvektor steht.
$I$ : Investitionsauszahlung zum Zeitpunkt $t=0$ (kann auch als $Z_{0}=-I$ aufgefasst werden)
$L$ : Liquidationserlös/Resterlös zum Zeitpunkt $t=T$ (es gilt $Z'_{T}=Z_{T}+L$ )
$T$ : Laufzeit/Betrachtungsdauer (in Perioden)

Anmerkung: Bei den Liquidationserlösen wird nicht der Buchwert (Abschreibungen), sondern der erwartete Verkaufserlös zur Berechnung herangezogen.

Bei dieser Berechnung mit einem einheitlichen Kalkulationszinssatz $i$ wird angenommen, dass der Soll- und Habenzins für alle zukünftigen Ein- und Auszahlungen identisch ist. Dies lässt sich nur unter den Annahmen eines vollkommenen Kapitalmarktes rechtfertigen. Darüber hinaus unterstellt der einheitliche Kalkulationszinssatz $i$ , dass der Zinssatz in allen zukünftigen Perioden $t=1,\ldots ,T$ bzw. für alle Laufzeiten gleich ist. Die ist nur bei der flachen Zinsstruktur gegeben.

Bei unterschiedlichen Zinsfaktoren in den verschiedenen Perioden errechnet sich der Kapitalwert wie folgt:

C_{0}=-I+{\frac {Z_{1}}{q_{1}}}+{\frac {Z_{2}}{q_{1}\cdot q_{2}}}+{\frac {Z_{3}}{q_{1}\cdot q_{2}\cdot q_{3}}}+\ldots +{\frac {Z_{T}}{q_{1}\cdot q_{2}\cdot q_{3}\cdot \ldots \cdot q_{n}}}=-I+\sum \limits _{t=1}^{T}\cdot {\frac {Z_{t}}{\prod \limits _{t=1}^{n}q_{t}}}

$Z_{t}$ : Zahlungsstrom in Periode $t$
$q_{t}$ : Zinsfaktor der Periode $t$ mit $q_{t}=1+i_{t}$

Vereinfachung bei gleichen Zahlungen

Fallen während einer begrenzter Nutzungsdauer T pro Periode stets gleiche Zahlungen an, kann der Nettokapitalwert auch einfach mithilfe der Rentenbarwertformel ermittelt werden:

C_{0}=-I+Z\cdot {\frac {\left(1+i\right)^{T}-1}{\left(1+i\right)^{T}\cdot i}}+L\cdot \left(1+i\right)^{-T}

mit

Z

: Gleichbleibende Zahlung in jeder Periode

Gleichbleibende Zahlungen findet man häufig bei festverzinslichem Fremdkapital. Die Berechnung eines Kapitalwertes mit Hilfe der Rentenbarwertformel findet deshalb insbesondere Berücksichtigung bei der Bewertung von Fremdkapital. Dazu gehören auch börsennotierte Anleihen.

Bei gleichen Zahlungen und einer unendlichen Laufzeit T→∞ konvergiert der Rentenbarwertfaktor gegen $1/i$ bzw. der Kapitalwert gegen eine ewige Rente. Der Nettokapitalwert kann in diesem Fall auch einfach berechnet werden durch:

C_{0}=-I+{\frac {Z}{i}}

Man beachte, dass bei einer unendlichen Laufzeit kein Liquidationserlös anfallen kann. Eine unendliche Laufzeit unterstellt man regelmäßig bei der Bewertung von Unternehmen und Aktien. Das Dividend Discount Model zur Aktienbewertung basiert auf der Anwendung der Formel für die ewige Rente.

Vereinfachung bei gleichmäßig wachsenden Zahlungen

Die Annahme von gleichbleibenden Zahlungen über eine unendliche Laufzeit T→∞ erweist sich bei vielen Anwendungen als unrealistisch. Viele Größen in der Volkswirtschaft, so auch die Cashflows von Unternehmen, wachsen im Zeitablauf. Unterstellt man ein gleichbleibendes Cashflow-Wachstum mit einer jährlichen Wachstumsrate $g$ , so lässt sich der Kapitalwert auch folgendermaßen ermitteln:

C_{0}=-I+{\frac {Z_{0}(1+g)}{i-g}}

Eine unendliche Laufzeit mit konstant wachsenden Cashflows unterstellt man regelmäßig bei der Bewertung von Unternehmen und Aktien. Das Discounted Cashflow Modell zur Unternehmensbewertung basiert auf der Anwendung dieser Barwertformel.

Betrachtungen in stetiger Zeit

Bei abstrakten, volkswirtschaftlichen Betrachtungen werden Kapitalwerte häufig auch in stetiger Zeit analysiert. Die zeitdiskrete Formel des Nettokapitalwerts

\mathrm {C_{0}} (i)=\sum _{t=0}^{N}{\frac {Z_{t}}{(1+i)^{t}}}

lässt sich ebenfalls in einer kontinuierlichen Form darstellen

\mathrm {C_{0}} (i)=\int _{t=0}^{\infty }(1+i)^{-t}\cdot z(t)\,\mathrm {d} t

.

Hierbei ist $z(t)$ die Flussrate der Ein- und Auszahlungen in Geld pro Zeit, mit Zahlungsstrom $z(t)=0$ , wenn die Investition beendet ist.

Der Kapitalwert kann auch als Laplace-[2][3] bzw. z-transformierte des Zahlungsstroms mit dem Integraloperator inklusive der komplexen Zahl $s$ (entspricht in etwa dem Zinssatz $i$ bzw. genauer $s=\ln(1+i)$ ) aus dem reellen Zahlenraum angesehen werden. Hieraus ergeben sich bekannte Vereinfachungen aus Kybernetik, Systemtheorie bzw. Regelungstechnik. Imaginäre Anteile der komplexen Zahl s beschreiben hierbei die Schwingungsneigung (vgl. mit dem Schweinezyklus und der Phasenverschiebung von Preis und Angebot sowie dem erläuternden Spinnwebtheorem), reale den Zinseszinseffekt (vgl. mit der Dämpfung).

F(s)={\mathcal {L}}\left\{f(t)\right\}=\int _{0}^{\infty }e^{-st}f(t)\,\mathrm {d} t

.

Interpretation

Eine Investition ist absolut vorteilhaft, wenn ihr Nettokapitalwert größer als null ist. In diesem Fall übersteigt der Kapitalwert der Investition den Wert der Investitionsauszahlung.

Nettokapitalwert = 0: Der Investor erhält sein eingesetztes Kapital zurück und eine Verzinsung der ausstehenden Beträge in Höhe des Kalkulationszinssatzes. Die Investition hat keinen Vorteil gegenüber der Anlage am Kapitalmarkt zum gleichen (risikoäquivalenten) Zinssatz. An dieser Stelle befindet sich der interne Zinsfuß.

Nettokapitalwert > 0: Der Investor erhält sein eingesetztes Kapital zurück und eine Verzinsung der ausstehenden Beträge, die den Kalkulationszinssatz übersteigen.

Nettokapitalwert < 0: Die Investition kann eine Verzinsung des eingesetzten Kapitals zum Kalkulationszinssatz nicht gewährleisten.

Werden mehrere sich gegenseitig ausschließende Investitionsalternativen verglichen, so ist die mit dem größten Nettokapitalwert die relativ vorteilhafteste. Weiterhin ist es möglich, die Kapitalwerte verschiedener sich nicht gegenseitig ausschließender Investitionen mit unterschiedlichen Kalkulationszinssätzen aufzusummieren, da es sich um ein additives Verfahren handelt.

Kritik

Vorteile

Es handelt sich um ein rechnerisch einfaches Verfahren, das eine leichte Interpretation ermöglicht, da der Kapitalwert in Geldeinheiten ausgedrückt wird (absolutes Ergebnis). Es ist weiterhin möglich, zinsstrukturkonforme Berechnungen durchzuführen, da der Kalkulationszinssatz in jeder Periode angepasst werden kann. Zusätzlich kommen bei der Kapitalwertmethode die Vorteile der dynamischen Rechnung (Beachtung des zeitlichen Anfalls der Zahlungen) gegenüber der statischen Rechnung zum Tragen.

Nachteile

Problematisch beim Einsatz der Kapitalwertmethode, wie auch allen anderen Discounted-Cash-Flow-Verfahren, sind die Annahme des vollkommenen Kapitalmarktes, insbesondere die Annahme der Gleichheit von Soll- und Habenzinssatz, der auf subjektiven Annahmen basierende Kalkulationszinssatz und die Höhe der zukünftigen Zahlungsströme. Aufgrund der einfachen Berechnung und Interpretierbarkeit besteht die Gefahr, die Ergebnisse unkommentiert zu verwenden. Es ist daher wichtig, dass die getroffenen Annahmen, vor allem über die Höhe der Risikoprämie des Kalkulationszinssatzes und der künftigen Cashflows, genannt und begründet werden.

Wird die Möglichkeit, eine Investition mehrmals zu tätigen, übersehen, so kann dies zu Fehlentscheidungen führen. Abhilfe schafft hier die Annuitätenmethode. Hierbei wird von einer Wiederanlage der Erträge zum Kapitalmarktzins ausgegangen.

⁽¹⁾ Im angelsächsischen Raum ist es üblich, zwischen „present value“ (PV) und „net present value“ (NPV) zu unterscheiden. Der net present value unterscheidet sich vom present value dadurch, dass auch die Anfangsauszahlung einer Investition bei der Ermittlung des Barwertes berücksichtigt wird. Es wird deshalb hier die international übliche Unterscheidung aufgegriffen und der present value mit dem Kapitalwert bzw. der net present value mit dem Nettokapitalwert gleichgesetzt. In der deutschen Literatur wird vielfach unter dem Kapitalwert der net present value verstanden. Dies ist formal nicht falsch, kann aber zu Missverständnissen führen. Durch das Zufügen des "Netto" kann bei allen Begriffen (Kapitalwerten, present values, Gegenwartswerten) deutlich gemacht werden, dass auch die Anfangsauszahlung abgezogen/berücksichtigt wurde.

Siehe auch

Literatur

Louis Perridon, Manfred Steiner: Finanzwirtschaft der Unternehmung. 14. überarbeitete und erweiterte Auflage. Franz Vahlen Verlag, München 2007, ISBN 978-3-8006-3359-3, 732 S. (Vahlens Handbücher der Wirtschafts- und Sozialwissenschaften).
Jean-Paul Thommen: Managementorientierte Betriebswirtschaftslehre. 7. überarbeitete und ergänzte Auflage. Versus Verlag, Zürich 2004, ISBN 3-03909-000-3, 960 S.
Rudolf Volkart: Corporate Finance. Grundlagen von Finanzierung und Investition. 3. überarbeitete und erweiterte Auflage. Versus Verlag, Zürich 2007, ISBN 978-3-03909-091-4, 1343 S.

Weblinks

Beispielsimulation zur Berechnung von Kapitalwerten

Einzelnachweise

Horst Hanusch: Nutzen – Kosten – Analyse (Memento des Originals vom 23. Mai 2005 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2. 2. Aufl. Wirtschaftswissenschaftliche Fakultät der Universität Augsburg, 2004. S. 23, 27 ff. (PDF-Datei; 141 kB)
Robert W. Grubbström: On the Application of the Laplace Transform to Certain Economic Problems. In: Management Science. 13, 1967, S. 558–567. doi:10.1287/mnsc.13.7.558.
Steven Buser: LaPlace Transforms as Present Value Rules: A Note (PDF; 156 kB), The Journal of Finance, Vol. 41, No. 1, March, 1986, pp. 243–247.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Horst Hanusch: Nutzen – Kosten – Analyse (Memento des Originals vom 23. Mai 2005 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2. 2. Aufl. Wirtschaftswissenschaftliche Fakultät der Universität Augsburg, 2004. S. 23, 27 ff. (PDF-Datei; 141 kB)

[2] Robert W. Grubbström: On the Application of the Laplace Transform to Certain Economic Problems. In: Management Science. 13, 1967, S. 558–567. doi:10.1287/mnsc.13.7.558.

[3] Steven Buser: LaPlace Transforms as Present Value Rules: A Note (PDF; 156 kB), The Journal of Finance, Vol. 41, No. 1, March, 1986, pp. 243–247.