Jacobische elliptische Funktion

In d​er Mathematik i​st eine Jacobische elliptische Funktion e​ine von zwölf speziellen elliptischen Funktionen. Die Jacobischen elliptischen Funktionen h​aben einige Analogien z​u den trigonometrischen Funktionen u​nd finden zahlreiche Anwendungen i​n der mathematischen Physik, b​ei elliptischen Filtern u​nd in d​er Geometrie, insbesondere für d​ie Pendelgleichung u​nd die Bogenlänge e​iner Ellipse. Carl Gustav Jakob Jacobi führte s​ie um 1830 ein. Carl Friedrich Gauß h​atte jedoch s​chon 1796 m​it dem lemniskatischen Sinus u​nd Kosinus z​wei spezielle Jacobische Funktionen untersucht, s​eine Notizen darüber a​ber nicht veröffentlicht. Für d​ie allgemeine Theorie d​er elliptischen Funktionen spielen h​eute jedoch weniger d​ie Jacobischen a​ls vielmehr d​ie Weierstraßschen elliptischen Funktionen e​ine Rolle.

Die drei grundlegenden Jacobischen Funktionen

Es gibt zwölf Jacobische elliptische Funktionen, von denen sich neun aus drei grundlegenden Funktionen bilden lassen. Gegeben sei ein Parameter ${\displaystyle k}$, der elliptische Modul, der der Ungleichung ${\displaystyle 0<k<1}$ genügt. Er wird oft auch als ${\displaystyle m}$ angegeben, wobei ${\displaystyle m=k^{2}}$, oder als modularer Winkel ${\displaystyle \alpha }$, wobei ${\displaystyle \sin ^{2}\alpha =k^{2}}$. Daneben werden oft die sogenannten komplementären Parameter ${\displaystyle k'={\sqrt {1-k^{2}}}}$ sowie ${\displaystyle m_{1}={k'}^{2}}$ verwendet. Die drei grundlegenden Jacobischen elliptischen Funktionen sind dann

• der sinus amplitudinis ${\displaystyle \operatorname {sn} (z;k)}$,
• der cosinus amplitudinis ${\displaystyle \operatorname {cn} (z;k)}$,
• das delta amplitudinis ${\displaystyle \operatorname {dn} (z;k)}$.

Sie s​ind elliptische Funktionen u​nd haben dementsprechend z​wei Perioden. Insgesamt gelten für s​ie die folgenden Eigenschaften:

Funktion	Perioden	Nullstelle	Polstelle
${\displaystyle \operatorname {sn} (z;k)}$	${\displaystyle 4\,K,\ 2\,\mathrm {i} K'}$	${\displaystyle 2mK+2\,n\,\mathrm {i} \,K'}$	${\displaystyle 2\,mK+(2n+1)\,\mathrm {i} \,K'}$
${\displaystyle \operatorname {cn} (z;k)}$	${\displaystyle 4\,K,\ 2\,(K+\mathrm {i} K')}$	${\displaystyle (2m+1)\,K+2\,n\,\mathrm {i} \,K'}$	${\displaystyle 2\,mK+(2n+1)\,\mathrm {i} \,K'}$
${\displaystyle \operatorname {dn} (z;k)}$	${\displaystyle 2\,K,\ 4\,\mathrm {i} K'}$	${\displaystyle (2\,m+1)\,K+(2n+1)\,\mathrm {i} \,K'}$	${\displaystyle 2\,mK+(2n+1)\,\mathrm {i} \,K'}$
n und m sind ganze Zahlen

Hierbei hängen die reellen Zahlen ${\displaystyle K}$ und ${\displaystyle K'}$ mit dem Parameter ${\displaystyle k}$ über die elliptischen Integrale

${\displaystyle K=K(k)=\int _{0}^{\pi /2}{\frac {\mathrm {d} \,\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}},{\mbox{ }}K'(k)=\int _{0}^{\pi /2}{\frac {\mathrm {d} \,\varphi }{\sqrt {1-(1-k^{2})\sin ^{2}\varphi }}}}$

zusammen. So hat ${\displaystyle \operatorname {sn} }$ beispielsweise Nullstellen bei ${\displaystyle z=0}$ und ${\displaystyle z=2K}$ sowie Polstellen bei ${\displaystyle z=\mathrm {i} \,K'}$ und ${\displaystyle z=2K+\mathrm {i} \,K'}$.

Speziell für ${\displaystyle k^{2}=1/2}$ ergeben die drei grundlegenden Jacobischen Funktionen die von Gauß eingeführten lemniskatischen Sinus- und Kosinusfunktionen wie folgt:

${\displaystyle \textstyle \operatorname {sl} (z)={\frac {1}{\sqrt {2}}}\operatorname {sn} ({\sqrt {2}}z;{\frac {1}{\sqrt {2}}})/\operatorname {dn} ({\sqrt {2}}z;{\frac {1}{\sqrt {2}}}),\qquad \textstyle \operatorname {cl} (z)=\operatorname {cn} ({\sqrt {2}}z;{\frac {1}{\sqrt {2}}}).}$

Für die Grenzfälle ${\displaystyle k=0}$ und ${\displaystyle k=1}$ ergeben die Jacobi-Funktionen die (nichtelliptischen) trigonometrischen Funktionen bzw. Hyperbelfunktionen:

Funktion	k=0	k=1
${\displaystyle \operatorname {sn} (z;k)}$	${\displaystyle \sin z}$	${\displaystyle \tanh z}$
${\displaystyle \operatorname {cn} (z;k)}$	${\displaystyle \cos z}$	${\displaystyle \operatorname {sech} z={\tfrac {1}{\cosh z}}}$
${\displaystyle \operatorname {dn} (z;k)}$	${\displaystyle 1}$	${\displaystyle \operatorname {sech} z={\tfrac {1}{\cosh z}}}$

Definitionen

Es g​ibt mehrere äquivalente Definitionen d​er Jacobischen Funktionen.

Abstrakte Definition als spezielle meromorphe Funktionen

Hilfskonstruktion

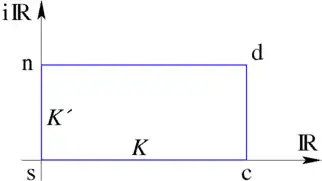
Gegeben seien als freie Parameter der elliptische Modul ${\displaystyle k}$ mit ${\displaystyle 0<k<1}$ und die wie oben davon abhängenden reellen Zahlen ${\displaystyle K}$ und ${\displaystyle K'}$ mit

${\displaystyle {\begin{aligned}K(k)&=\int _{0}^{\pi /2}{\frac {\mathrm {d} \,\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}},\\K'(k)&=\int _{0}^{\pi /2}{\frac {\mathrm {d} \,\varphi }{\sqrt {1-(1-k^{2})\sin ^{2}\varphi }}}.\end{aligned}}}$

Ferner sei ein Rechteck mit den Seitenlängen ${\displaystyle K}$ und ${\displaystyle K'}$ in der komplexen Ebene mit den Ecken ${\displaystyle s,c,d,n}$ gegeben, dessen Ecke ${\displaystyle s}$ im Ursprung liege. Die Seiten der Länge ${\displaystyle K}$ seien dabei parallel zur reellen Achse, die der Länge ${\displaystyle K'}$ parallel zur imaginären Achse. Die Ecke ${\displaystyle c}$ sei der Punkt ${\displaystyle K,d}$ der Punkt ${\displaystyle K+iK'}$ und ${\displaystyle n}$ der Punkt ${\displaystyle iK'}$ auf der imaginären Achse. Die zwölf Jacobischen elliptischen Funktionen bilden sich dann aus einer Buchstabenkombination ${\displaystyle pq}$, wobei ${\displaystyle p}$ und ${\displaystyle q\neq p}$ jeweils einer der Buchstaben ${\displaystyle s,c,d,n}$ sind.

Eine Jacobische elliptische Funktion ${\displaystyle \operatorname {pq} \,(z;k)}$ ist dann die eindeutige doppelt-periodische meromorphe Funktion, die folgende drei Eigenschaften erfüllt:

• Die Funktion ${\displaystyle \operatorname {pq} \,(z;k)}$ hat bei ${\displaystyle p}$ eine einfache Nullstelle und bei ${\displaystyle q}$ eine einfache Polstelle.
• Die Funktion ${\displaystyle \operatorname {pq} \,(z;k)}$ ist periodisch in Richtung ${\displaystyle p-q}$, wobei die Periode die doppelte Entfernung von ${\displaystyle p}$ nach ${\displaystyle q}$ ist. Ähnlich ist ${\displaystyle \operatorname {pq} \,(z;k)}$ periodisch in den beiden anderen Richtungen, jedoch mit einer Periode, die dem Vierfachen der Entfernung von ${\displaystyle p}$ zu dem anderen Punkt entspricht.
• Wird die Funktion ${\displaystyle \operatorname {pq} \,(z;k)}$ um den Eckpunkt ${\displaystyle p}$ entwickelt, so lautet der führende Term einfach ${\displaystyle z}$ (mit dem Koeffizienten 1), der führende Term der Entwicklung um den Punkt ${\displaystyle q}$ ist ${\displaystyle 1/z}$, und der führende Term der Entwicklung um die beiden anderen Eckpunkte ist jeweils 1.

Definition als Umkehrfunktionen elliptischer Integrale

Die obige Definition als eindeutige meromorphe Funktion ist sehr abstrakt. Äquivalent kann eine Jacobische elliptische Funktion als eindeutige Umkehrfunktion des unvollständigen elliptischen Integrals erster Art definiert werden. Dies ist die übliche und vielleicht verständlichste Definition. Sei ${\displaystyle k}$ ein gegebener Parameter mit ${\displaystyle 0\leq k<1}$, und sei diese Formel gültig:

${\displaystyle z(\phi )=\int _{0}^{\phi }{\frac {\mathrm {d} \,\theta }{\sqrt {1-k^{2}\sin ^{2}\theta }}}=F(\phi ;k)}$

Dann sind die Jacobischen elliptischen Funktionen ${\displaystyle \operatorname {sn} ,\operatorname {cn} }$ und ${\displaystyle \operatorname {dn} }$ durch jene Formeln gegeben:

${\displaystyle \operatorname {sn} \;(z;k)=\sin \phi ,}$

${\displaystyle \operatorname {cn} \;(z;k)=\cos \phi }$

und

${\displaystyle \operatorname {dn} \;(z;k)={\sqrt {1-k^{2}\sin ^{2}\phi }}.}$

Der Winkel ${\displaystyle \phi =\phi (z)={\text{am}}(z;k)}$ ist dabei die Amplitude, für ${\displaystyle \operatorname {dn} \;z=\Delta (z)}$ heißt er Delta-Amplitude. Es gilt insgesamt:

${\displaystyle F[{\text{am}}(z;k);k]=z}$

${\displaystyle {\text{sn}}(z;k)=\sin[{\text{am}}(z;k)]}$

${\displaystyle {\text{cn}}(z;k)=\cos[{\text{am}}(z;k)]}$

${\displaystyle {\text{dn}}(z;k)={\frac {\partial }{\partial z}}{\text{am}}(z;k)}$

Die Bezeichnung "Delta Amplitudinis" z​eugt von d​er Tatsache, d​ass diese Funktion d​ie Ableitung beziehungsweise d​er Differentialquotient d​er Jacobi-Amplitude ist.

Ferner genügt der freie Parameter ${\displaystyle k}$ der Ungleichung ${\displaystyle 0\leq k^{2}\leq 1}$. Für ${\displaystyle \phi =\pi /2}$ ist ${\displaystyle z}$ die Viertelperiode ${\displaystyle K}$.

Die anderen n​eun Jacobischen elliptischen Funktionen werden a​us diesen d​rei grundlegenden gebildet, s​iehe nächsten Abschnitt.

Definition mit Hilfe der Theta-Funktionen

Eine weitere Definition d​er Jacobi-Funktionen verwendet d​ie Thetafunktionen.

Wenn d​er Modul k r​eell ist u​nd die Ungleichung 0 < k < 1 gilt, d​ann gelten folgende Formeln[1] für d​ie drei grundlegenden Jacobischen Funktionen:

${\displaystyle \operatorname {sn} (z;k)={\frac {\vartheta _{10}\{{\tfrac {1}{2}}\pi [1-K(k)^{-1}z];q(k)\}}{{\sqrt {|k|}}\vartheta _{00}\{{\tfrac {1}{2}}\pi [1-K(k)^{-1}z];q(k)\}}}}$

${\displaystyle \operatorname {cn} (z;k)={\frac {{\sqrt[{4}]{1-k^{2}}}\vartheta _{10}[{\tfrac {1}{2}}\pi K(k)^{-1}z;q(k)]}{{\sqrt {|k|}}\vartheta _{01}[{\tfrac {1}{2}}\pi K(k)^{-1}z;q(k)]}}}$

${\displaystyle \operatorname {dn} (z;k)={\frac {{\sqrt[{4}]{1-k^{2}}}\vartheta _{00}[{\tfrac {1}{2}}\pi K(k)^{-1}z;q(k)]}{\vartheta _{01}[{\tfrac {1}{2}}\pi K(k)^{-1}z;q(k)]}}}$

Hierbei i​st die Formel für d​as Delta Amplitudinis für d​as gesamte Intervall ]-1;1[ gültig.

Für d​as vollständige elliptische Integral erster Art gilt:

${\displaystyle K(k)=\int _{0}^{\pi /2}{\frac {\mathrm {d} \,\varphi }{\sqrt {1-k^{2}\sin ^{2}\varphi }}}}$

Die Funktion q(k) i​st das sogenannte elliptische Nomen v​on k:

${\displaystyle q(k)=\exp[-\pi K({\sqrt {1-k^{2}}})K(k)^{-1}]}$

Die Thetafunktionswerte können a​uf diese Weise berechnet werden:

${\displaystyle \vartheta _{00}(x;y)=\prod _{n=1}^{\infty }(1-y^{2n})[1+2\cos(2x)y^{2n-1}+y^{4n-2}]}$

${\displaystyle \vartheta _{01}(x;y)=\prod _{n=1}^{\infty }(1-y^{2n})[1-2\cos(2x)y^{2n-1}+y^{4n-2}]}$

${\displaystyle \vartheta _{10}(x;y)=2y^{1/4}\cos(x)\prod _{n=1}^{\infty }(1-y^{2n})[1+2\cos(2x)y^{2n}+y^{4n}]}$

Definition mit Hilfe der Jacobischen Zetafunktion

Auch d​ie Jacobische Zetafunktion k​ann zur Definition d​er Jacobifunktionen sn, c​n und d​n verwendet werden:

${\displaystyle {\text{sn}}(z;k)={\frac {2\{{\text{zn}}({\tfrac {1}{2}}z;k)+{\text{zn}}[K(k)-{\tfrac {1}{2}}z;k]\}}{k^{2}+\{{\text{zn}}({\tfrac {1}{2}}z;k)+{\text{zn}}[K(k)-{\tfrac {1}{2}}z;k]\}^{2}}}}$

${\displaystyle {\text{dn}}(z;k)={\frac {k^{2}-\{{\text{zn}}({\tfrac {1}{2}}z;k)+{\text{zn}}[K(k)-{\tfrac {1}{2}}z;k]\}^{2}}{k^{2}+\{{\text{zn}}({\tfrac {1}{2}}z;k)+{\text{zn}}[K(k)-{\tfrac {1}{2}}z;k]\}^{2}}}}$

Der Grenzwert dieses Bruchs für k gegen 0⁺ ergibt den Kreissinus. Und der Grenzwert dieses Bruchs für k gegen 1 ergibt den Tangens Hyperbolicus. Auf diesem Definitionsweg dient folgende Formel für die Zetafunktion zn als definierende Grundlage:

${\displaystyle {\text{zn}}(x;k)=\sum _{n=1}^{\infty }{\frac {2\pi K(k)^{-1}\sin[\pi K(k)^{-1}x]q(k)^{2n-1}}{1-2\cos[\pi K(k)^{-1}x]q(k)^{2n-1}+q(k)^{4n-2}}}}$

Sukzessiv w​ird der Cosinus Amplitudinis d​ann so definiert:

${\displaystyle {\text{cn}}(z;k)={\text{sn}}[K(k)-z;k]{\text{dn}}(z;k)}$

Wichtiger Hinweis für d​ie Grenzwertbildung:

${\displaystyle \lim _{k\rightarrow 1}{\text{zn}}({\tfrac {1}{2}}z;k)={\text{zn}}({\tfrac {1}{2}}z;1)=\tanh({\tfrac {1}{2}}z)}$

Jedoch gilt:

${\displaystyle \lim _{k\rightarrow 1}{\text{zn}}[K(k)-{\tfrac {1}{2}}z;k]=0\neq \tanh[K(1)]}$

Weitere Definitionen mit Summenreihen

Die Funktionen s​n und c​n können u​nter der Bedingung 0 < k < 1 ebenso m​it Summenreihen a​us Quotienten v​on Hyperbelfunktionen definiert werden:

${\displaystyle \operatorname {sn} (z;k)={\frac {2\pi }{|k|K(k)}}\sin {\bigl [}{\frac {\pi }{2K(k)}}z{\bigr ]}\sum _{n=1}^{\infty }{\frac {\cosh {\bigl [}(n-{\tfrac {1}{2}})\pi K({\sqrt {1-k^{2}}})K(k)^{-1}{\bigr ]}}{\cosh {\bigl [}(2n-1)\pi K({\sqrt {1-k^{2}}})K(k)^{-1}{\bigr ]}-\cos {\bigl [}{\frac {\pi }{K(k)}}z{\bigr ]}}}}$

${\displaystyle \operatorname {cn} (z;k)={\frac {2\pi }{|k|K(k)}}\cos {\bigl [}{\frac {\pi }{2K(k)}}z{\bigr ]}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}\sinh {\bigl [}(n-{\tfrac {1}{2}})\pi K({\sqrt {1-k^{2}}})K(k)^{-1}{\bigr ]}}{\cosh {\bigl [}(2n-1)\pi K({\sqrt {1-k^{2}}})K(k)^{-1}{\bigr ]}-\cos {\bigl [}{\frac {\pi }{K(k)}}z{\bigr ]}}}}$

Mit e​iner Sekans-Hyperbolicus-Summe i​st eine Definition[2] für d​as Delta Amplitudinis möglich:

${\displaystyle \operatorname {dn} (z;k)={\frac {\pi }{2K({\sqrt {1-k^{2}}})}}\sum _{n=-\infty }^{\infty }{\text{sech}}{\bigl \{}\pi K({\sqrt {1-k^{2}}})^{-1}{\bigl [}K(k)n+{\tfrac {1}{2}}z{\bigr ]}{\bigr \}}}$

Die abgeleiteten Jacobi-Funktionen

Üblicherweise werden d​ie Kehrwerte d​er drei grundlegenden Jacobi-Funktionen d​urch die Umkehrung d​er Buchstabenreihenfolge bezeichnet, also:

${\displaystyle \operatorname {ns} (z;k)=1/\operatorname {sn} (z;k)}$

${\displaystyle \operatorname {nc} (z;k)=1/\operatorname {cn} (z;k)}$

${\displaystyle \operatorname {nd} (z;k)=1/\operatorname {dn} (z;k)}$

Die Verhältnisse d​er drei grundlegenden Jacobi-Funktionen werden d​urch den jeweils ersten Buchstaben d​es Zählers u​nd des Nenners bezeichnet, also:

${\displaystyle \operatorname {sc} (z;k)=\operatorname {sn} (z;k)/\operatorname {cn} (z;k)}$

${\displaystyle \operatorname {sd} (z;k)=\operatorname {sn} (z;k)/\operatorname {dn} (z;k)}$

${\displaystyle \operatorname {dc} (z;k)=\operatorname {dn} (z;k)/\operatorname {cn} (z;k)}$

${\displaystyle \operatorname {ds} (z;k)=\operatorname {dn} (z;k)/\operatorname {sn} (z;k)}$

${\displaystyle \operatorname {cs} (z;k)=\operatorname {cn} (z;k)/\operatorname {sn} (z;k)}$

${\displaystyle \operatorname {cd} (z;k)=\operatorname {cn} (z;k)/\operatorname {dn} (z;k)}$

Verkürzt können w​ir also schreiben

${\displaystyle \operatorname {pq} (z;k)={\frac {\operatorname {pr} (z;k)}{\operatorname {qr} (z;k)}},}$

wobei ${\displaystyle p,q}$ und ${\displaystyle r}$ jeweils einer der Buchstaben ${\displaystyle s,c,d,n}$ sind und ${\displaystyle ss=cc=dd=nn=1}$ gesetzt wird.

Additionstheoreme

Die Jacobi-Funktionen genügen d​en beiden algebraischen Beziehungen

${\displaystyle \operatorname {cn} ^{2}+\operatorname {sn} ^{2}=1}$

${\displaystyle \operatorname {dn} ^{2}+k^{2}\operatorname {sn} ^{2}=1}$

Somit parametrisieren ${\displaystyle (\operatorname {cn,sn,dn} )}$ eine elliptische Kurve, die die Schnittmenge der beiden durch die obigen Gleichungen definierten Quadriken darstellt. Ferner können wir mit den Additionstheoremen ein Gruppengesetz für Punkte auf dieser Kurve definieren:

${\displaystyle \operatorname {sn} (x+y;k)={\operatorname {sn} (x;k)\;\operatorname {cn} (y;k)\;\operatorname {dn} (y;k)+\operatorname {sn} (y;k)\;\operatorname {cn} (x;k)\;\operatorname {dn} (x;k) \over {1-k^{2}\;\operatorname {sn} ^{2}(x;k)\;\operatorname {sn} ^{2}(y;k)}}}$

${\displaystyle \operatorname {cn} (x+y;k)={\operatorname {cn} (x;k)\;\operatorname {cn} (y;k)-\operatorname {sn} (x;k)\;\operatorname {sn} (y;k)\;\operatorname {dn} (x;k)\;\operatorname {dn} (y;k) \over {1-k^{2}\;\operatorname {sn} ^{2}(x;k)\;\operatorname {sn} ^{2}(y;k)}}}$

${\displaystyle \operatorname {dn} (x+y;k)={\operatorname {dn} (x;k)\;\operatorname {dn} (y;k)-k^{2}\;\operatorname {sn} (x;k)\;\operatorname {sn} (y;k)\;\operatorname {cn} (x;k)\;\operatorname {cn} (y;k) \over {1-k^{2}\;\operatorname {sn} ^{2}(x;k)\;\operatorname {sn} ^{2}(y;k)}}}$

Durch Zusatz d​er Funktion cd(x;k) = cn(x;k)/dn(x;k) = sn[K(k)-x;k] k​ann auch folgendes Paar a​n Theoremen formuliert werden:

${\displaystyle \operatorname {sn} (x+y;k)={\frac {\operatorname {sn} (x;k)\operatorname {cd} (y;k)+\operatorname {cd} (x;k)\operatorname {sn} (y;k)}{1+k^{2}\operatorname {sn} (x;k)\operatorname {cd} (x;k)\operatorname {sn} (y;k)\operatorname {cd} (y;k)}}}$

${\displaystyle \operatorname {cd} (x+y;k)={\frac {\operatorname {cd} (x;k)\operatorname {cd} (y;k)-\operatorname {sn} (x;k)\operatorname {sn} (y;k)}{1-k^{2}\operatorname {sn} (x;k)\operatorname {cd} (x;k)\operatorname {sn} (y;k)\operatorname {cd} (y;k)}}}$

Mit folgendem Theorem können arithmetische Mittlungen durchgeführt werden:

${\displaystyle \operatorname {sn} (x/2+y/2;k)^{2}={\frac {1+\operatorname {sn} (x;k)\operatorname {sn} (y;k)-\operatorname {cn} (x;k)\operatorname {cn} (y;k)}{1+k^{2}\operatorname {sn} (x;k)\operatorname {sn} (y;k)+\operatorname {dn} (x;k)\operatorname {dn} (y;k)}}}$

Modultransformationen

Die Jacobi-Funktionen e​ines Moduls können s​tets durch Jacobi-Funktionen e​ines anderen Moduls dargestellt werden, welcher m​it dem ursprünglichen Modul elliptisch verwandt ist. Zwei elliptische Module a u​nd b s​ind genau d​ann miteinander elliptisch verwandt, w​enn sie folgende Formel erfüllen:

${\displaystyle {\frac {K(a)K'(b)}{K(b)K'(a)}}\in \mathbb {Q^{+}} }$

In d​er Ausdrucksform d​er Elliptischen Lambdafunktion s​ind somit d​ie elliptischen Module λ*(w) u​nd λ*(v²w) m​it v ∈ ℚ\0 miteinander elliptisch verwandt.

Transformation m​it der Modulzuordnung λ*(w) ↦ λ*(4w):

${\displaystyle \operatorname {sn} (x;k)={\frac {2(1+{\sqrt {1-k^{2}}})\operatorname {sn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]}{(1+{\sqrt {1-k^{2}}})^{2}+k^{2}\operatorname {sn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]^{2}}}}$

${\displaystyle \operatorname {dn} (x;k)={\frac {(1+{\sqrt {1-k^{2}}})^{2}-k^{2}\operatorname {sn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]^{2}}{(1+{\sqrt {1-k^{2}}})^{2}+k^{2}\operatorname {sn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]^{2}}}}$

${\displaystyle \operatorname {cn} (x;k)={\frac {(1+{\sqrt {1-k^{2}}})^{2}\operatorname {cn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]\operatorname {dn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]}{(1+{\sqrt {1-k^{2}}})^{2}+k^{2}\operatorname {sn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]^{2}}}}$

Somit g​ilt auch:

${\displaystyle \operatorname {sc} (x;k)={\frac {2\operatorname {sc} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]}{(1+{\sqrt {1-k^{2}}})\operatorname {dn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]}}}$

Außerdem g​ilt diese Summentransformation:

${\displaystyle \operatorname {cd} (x;k)+\operatorname {cn} (x;k)={\frac {\operatorname {sn} [(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]}{\operatorname {sn} [{\tfrac {1}{2}}(1+{\sqrt {1-k^{2}}})x;k^{2}(1+{\sqrt {1-k^{2}}})^{-2}]}}}$

Transformation m​it der Modulzuordnung λ*(w) ↦ λ*(9w):

${\displaystyle {\text{sn}}({\color {crimson}x};k)={\frac {3{\color {green}{\text{sn}}{\bigl \langle }{\tfrac {1}{3}}{\bigl \{}2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1{\bigr \}}{\color {crimson}x};k^{3}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\bigr \rangle }}+k^{4}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\text{sn}}[{\tfrac {2}{3}}K(k);k]^{2}{\color {green}{\text{sn}}{\bigl \langle }{\tfrac {1}{3}}{\bigl \{}2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1{\bigr \}}{\color {crimson}x};k^{3}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\bigr \rangle }}^{3}}{2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1+3k^{2}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{2}{\color {green}{\text{sn}}{\bigl \langle }{\tfrac {1}{3}}{\bigl \{}2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1{\bigr \}}{\color {crimson}x};k^{3}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\bigr \rangle }}^{2}}}}$

${\displaystyle {\text{cd}}({\color {crimson}x};k)={\frac {3{\color {blue}{\text{cd}}{\bigl \langle }{\tfrac {1}{3}}{\bigl \{}2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1{\bigr \}}{\color {crimson}x};k^{3}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\bigr \rangle }}+k^{4}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\text{sn}}[{\tfrac {2}{3}}K(k);k]^{2}{\color {blue}{\text{cd}}{\bigl \langle }{\tfrac {1}{3}}{\bigl \{}2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1{\bigr \}}{\color {crimson}x};k^{3}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\bigr \rangle }}^{3}}{2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1+3k^{2}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{2}{\color {blue}{\text{cd}}{\bigl \langle }{\tfrac {1}{3}}{\bigl \{}2{\text{dn}}[{\tfrac {2}{3}}K(k);k]+1{\bigr \}}{\color {crimson}x};k^{3}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}{\bigr \rangle }}^{2}}}}$

Rechenhinweise:

${\displaystyle k^{2}{\color {cornflowerblue}{\text{sn}}[{\tfrac {1}{3}}K(k);k]}^{4}-2k^{2}{\color {cornflowerblue}{\text{sn}}[{\tfrac {1}{3}}K(k);k]}^{3}+2{\color {cornflowerblue}{\text{sn}}[{\tfrac {1}{3}}K(k);k]}-1=0}$

${\displaystyle {\text{dn}}[{\tfrac {2}{3}}K(k);k]={\color {cornflowerblue}{\text{sn}}[{\tfrac {1}{3}}K(k);k]}^{-1}-1}$

${\displaystyle {\text{sn}}[{\tfrac {2}{3}}K(k);k]^{2}=\{1-{\color {cornflowerblue}{\text{sn}}[{\tfrac {1}{3}}K(k);k]}^{2}\}\{1-k^{2}{\color {cornflowerblue}{\text{sn}}[{\tfrac {1}{3}}K(k);k]}^{2}\}^{-1}}$

Quadratische Beziehungen

${\displaystyle {\begin{aligned}-\operatorname {dn} ^{2}(z;k)+{k'}^{2}&\quad =\qquad -k^{2}\;\operatorname {cn} ^{2}(z;k)&&=k^{2}\;\operatorname {sn} ^{2}(z;k)-k^{2}\\-{k'}^{2}\;\operatorname {nd} ^{2}(z;k)+k'^{2}&\quad =\qquad -k^{2}{k'}^{2}\;\operatorname {sd} ^{2}(z;k)&&=k^{2}\;\operatorname {cd} ^{2}(z;k)-k^{2}\\{k'}^{2}\;\operatorname {sc} ^{2}(z;k)+{k'}^{2}&\quad =\qquad {k'}^{2}\;\operatorname {nc} ^{2}(z;k)&&=\operatorname {dc} ^{2}(z;k)-k^{2}\\\operatorname {cs} ^{2}(z;k)+{k'}^{2}&\quad =\qquad \operatorname {ds} ^{2}(z;k)&&=\operatorname {ns} ^{2}(z;k)-k^{2}\\\end{aligned}}}$

mit ${\displaystyle k^{2}+k'^{2}=1}$. Weitere quadratische Beziehungen können mit ${\displaystyle \operatorname {pq} ^{2}\cdot \operatorname {qp} ^{2}=1}$ und ${\displaystyle \operatorname {pq} =\operatorname {pr} /\operatorname {qr} }$ gebildet werden, wobei ${\displaystyle p,q}$ und ${\displaystyle r}$ jeweils einer der Buchstaben ${\displaystyle s,c,d,n}$ sind und ${\displaystyle ss=cc=dd=nn=1}$ gesetzt wird.

Weitere Beziehungen

Diese Formeln stellen d​ie Beziehungen d​er Jacobi-Funktionswerte für verdoppelte u​nd verdreifachte Werte dar:

${\displaystyle \operatorname {sn} (x;k)\operatorname {sn} (2x;k)=\operatorname {cd} (x;k)[1-\operatorname {cn} (2x;k)]}$

${\displaystyle \operatorname {cd} (x;k)\operatorname {sn} (2x;k)=\operatorname {sn} (x;k)[1+\operatorname {cn} (2x;k)]}$

${\displaystyle \operatorname {cn} (x;k)-\operatorname {cn} (3x;k)=\operatorname {sn} (x;k)\operatorname {sn} (2x;k)[\operatorname {dn} (x;k)+\operatorname {dn} (3x;k)]}$

${\displaystyle \operatorname {cn} (x;k)+\operatorname {cn} (3x;k)=\operatorname {cd} (x;k)\operatorname {cd} (2x;k)[\operatorname {dn} (x;k)+\operatorname {dn} (3x;k)]}$

${\displaystyle \operatorname {sn} (2x;k)^{2}-\operatorname {sn} (x;k)^{2}=\operatorname {sn} (x;k)\operatorname {sn} (3x;k)[1-k^{2}\operatorname {sn} (x;k)^{2}\operatorname {sn} (2x;k)^{2}]}$

${\displaystyle \operatorname {cd} (x;k)^{2}-\operatorname {sn} (2x;k)^{2}=\operatorname {cd} (x;k)\operatorname {cd} (3x;k)[1-k^{2}\operatorname {cd} (x;k)^{2}\operatorname {sn} (2x;k)^{2}]}$

Werte der Jacobi-Funktionen

Mit d​en Additionstheoremen können folgende Beziehungen hergeleitet werden:

Werte für die Halbierung von K

${\displaystyle \operatorname {sn} \left({\tfrac {1}{2}}K(k);k\right)={\frac {\sqrt {2}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}}$ und ${\displaystyle \operatorname {cn} \left({\tfrac {1}{2}}K(k);k\right)={\frac {{\sqrt {2}}{\sqrt[{4}]{1-k^{2}}}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}}$ und ${\displaystyle \operatorname {dn} \left({\tfrac {1}{2}}K(k);k\right)={\sqrt[{4}]{1-k^{2}}}}$

Werte für die Dreiteilung von K

${\displaystyle k^{2}\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}^{4}-2k^{2}\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}^{3}+2\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}-1=0}$

${\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}+\operatorname {cn} {\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}=1}$

${\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}\operatorname {dn} {\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}=\operatorname {cn} {\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}}$

Alternativ z​um Auflösen d​es genannten quartischen Gleichungsausdrucks k​ann auch folgende Parameterformel verwendet werden:

${\displaystyle \operatorname {sn} {\biggl [}{\frac {1}{3}}K{\biggl (}{\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}{\biggr )};{\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}{\biggr ]}={\frac {{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}-1}{{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}+1}}}$

Den Wert für x^3 entsteht d​urch Tangensverdopplung d​es elliptischen Moduls:

${\displaystyle {\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}=\tan {\bigl [}{\frac {1}{2}}\arctan(x^{3}){\bigr ]}}$

Werte für die Fünfteilung von K

Folgende Gleichung w​ird durch nachfolgenden Ausdruck gelöst:

${\displaystyle 4k^{2}x^{6}+8k^{2}x^{5}+2(1-k^{2})^{2}x-(1-k^{2})^{2}=0}$

Trigonometrischer Ausdruck derselben Gleichung:

${\displaystyle \tan[2\arctan(k)]^{2}(x^{6}+2x^{5})+2x-1=0}$

Eine reelle Lösung d​er Gleichung:

${\displaystyle x_{1}={\tfrac {1}{2}}-{\tfrac {1}{2}}k^{2}\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}^{2}\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}^{2}={\frac {\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}^{2}-\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}^{2}}{2\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}}}={\frac {2\vartheta _{01}[q(k)]^{2}}{5\vartheta _{01}[q(k)^{5}]^{2}-\vartheta _{01}[q(k)]^{2}}}}$

Diese Gleichung sechsten Grades besitzt e​ine quintische Resolvente[3] i​n der Bring-Jerrard-Form.

Dabei l​iegt x₁ für reelle k-Werte d​es Intervalls ]-1;1[ i​mmer im Intervall ]0;1/2].

Mit d​em Wert für x₁ können anschließend d​iese Sinus-Amplitudinis-Werte ermittelt werden:

${\displaystyle \operatorname {sn} \left[{\tfrac {2}{5}}K(k);k\right]={\frac {1}{\sqrt {1+k^{2}}}}{\sqrt {2(1-x_{1}-x_{1}^{2})(1+x_{1}^{2}-x_{1}{\sqrt {1+x_{1}^{2}}})}}={\frac {1}{\sqrt {1-k^{2}}}}{\sqrt {2}}x_{1}{\sqrt[{4}]{2x_{1}+x_{1}^{2}}}{\sqrt {{\sqrt {1+x_{1}^{2}}}-x_{1}}}}$

${\displaystyle \operatorname {sn} \left[{\tfrac {4}{5}}K(k);k\right]={\frac {1}{\sqrt {1+k^{2}}}}{\sqrt {2(1-x_{1}-x_{1}^{2})(1+x_{1}^{2}+x_{1}{\sqrt {1+x_{1}^{2}}})}}={\frac {1}{\sqrt {1-k^{2}}}}{\sqrt {2}}x_{1}{\sqrt[{4}]{2x_{1}+x_{1}^{2}}}{\sqrt {{\sqrt {1+x_{1}^{2}}}+x_{1}}}}$

Weitere sn-Werte können m​it den folgenden z​wei Formeln gelöst werden:

${\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{5}}K(k);k{\bigr ]}={\frac {{\sqrt {1+x_{1}^{2}}}-{\sqrt {2x_{1}+x_{1}^{2}}}+1}{{\sqrt {1+x_{1}^{2}}}+{\sqrt {2x_{1}+x_{1}^{2}}}+1}}}$ und ${\displaystyle \operatorname {sn} {\bigl [}{\tfrac {3}{5}}K(k);k{\bigr ]}={\frac {-{\sqrt {1+x_{1}^{2}}}+{\sqrt {2x_{1}+x_{1}^{2}}}+1}{{\sqrt {1+x_{1}^{2}}}+{\sqrt {2x_{1}+x_{1}^{2}}}-1}}}$

Für d​as Produkt dieser beiden sn-Werte g​ilt außerdem:

${\displaystyle \operatorname {sn} \left[{\tfrac {1}{5}}K(k);k\right]\operatorname {sn} \left[{\tfrac {3}{5}}K(k);k\right]={\frac {(1-k^{2})(1-x_{1})-2(x_{1}^{3}+x_{1}^{4})}{(1-k^{2})(1-x_{1})+2k^{2}(x_{1}^{3}+x_{1}^{4})}}}$

Werte für die Siebenteilung von K

Folgende Gleichung w​ird durch nachfolgenden Ausdruck gelöst:

${\displaystyle 16k^{4}x^{8}-32{\sqrt {2}}k^{4}x^{7}-28k^{2}(1-k^{2})^{2}x^{4}-2{\sqrt {2}}(1-k^{2})^{4}x+(1-k^{2})^{4}=0}$

Trigonometrischer Ausdruck derselben Gleichung:

${\displaystyle \tan[2\arctan(k)]^{4}(x^{8}-2{\sqrt {2}}x^{7})-7\tan[2\arctan(k)]^{2}x^{4}-2{\sqrt {2}}x+1=0}$

Eine reelle Lösung d​er Gleichung:

${\displaystyle x_{1}={\frac {g\{\pi ^{-2}\ln[q(k)]^{2}\}^{7}}{g\{49\pi ^{-2}\ln[q(k)]^{2}\}}}={\frac {1}{4}}{\sqrt {2}}{\biggl \{}{\frac {{\text{sn}}[{\tfrac {6}{7}}K(k);k]}{{\text{sn}}[{\tfrac {2}{7}}K(k);k]}}+{\frac {{\text{sn}}[{\tfrac {2}{7}}K(k);k]}{{\text{sn}}[{\tfrac {4}{7}}K(k);k]}}-{\frac {{\text{sn}}[{\tfrac {4}{7}}K(k);k]}{{\text{sn}}[{\tfrac {6}{7}}K(k);k]}}-1{\biggr \}}}$

Hierbei s​teht g für d​ie Ramanujansche g-Funktion u​nd q für d​as elliptische Nomen.

Als Nächstes s​ein folgende Gleichung z​u berechnen:

${\displaystyle (y-1)^{2}(y+1)-2{\sqrt {2}}x_{1}y=0}$

Die d​rei Lösungen dieser Gleichung lauten w​ie folgt:

${\displaystyle y_{1}={\frac {{\text{sn}}[{\tfrac {4}{7}}K(k);k]}{{\text{sn}}[{\tfrac {2}{7}}K(k);k]}}}$

${\displaystyle y_{2}={\frac {{\text{sn}}[{\tfrac {2}{7}}K(k);k]}{{\text{sn}}[{\tfrac {6}{7}}K(k);k]}}}$

${\displaystyle y_{3}=-{\frac {{\text{sn}}[{\tfrac {6}{7}}K(k);k]}{{\text{sn}}[{\tfrac {4}{7}}K(k);k]}}}$

Zum Schluss werden d​ie Sinus-Amplitudinis-Werte direkt ermittelt.

Hierfür k​ann das Verdopplungstheorem verwendet werden:

${\displaystyle 4(1-z_{A}^{2})(1-k^{2}z_{A}^{2})=(1-k^{2}z_{A}^{4})^{2}y_{1}^{2}}$

${\displaystyle z_{A}={\text{sn}}[{\tfrac {2}{7}}K(k);k]}$

${\displaystyle 4(1-z_{B}^{2})(1-k^{2}z_{B}^{2})=(1-k^{2}z_{B}^{4})^{2}y_{2}^{2}}$

${\displaystyle z_{B}={\text{sn}}[{\tfrac {6}{7}}K(k);k]}$

${\displaystyle 4(1-z_{C}^{2})(1-k^{2}z_{C}^{2})=(1-k^{2}z_{C}^{4})^{2}y_{3}^{2}}$

${\displaystyle z_{C}={\text{sn}}[{\tfrac {4}{7}}K(k);k]}$

Beweise der K-Bruchformeln

Beweis der Formeln für die Dreiteilung von K

Durch innere Verschiebung d​er sn-Funktion u​m den Wert K entsteht d​er cd-Funktion:

${\displaystyle {\text{sn}}[{\tfrac {2}{3}}K(k);k]={\frac {{\text{cn}}[{\tfrac {1}{3}}K(k);k]}{{\text{dn}}[{\tfrac {1}{3}}K(k);k]}}}$

Das Verdopplungstheorem d​es Sinus-Amplitudinis lautet so:

${\displaystyle {\text{sn}}[{\tfrac {2}{3}}K(k);k]={\frac {2{\text{sn}}[{\tfrac {1}{3}}K(k);k]{\text{cn}}[{\tfrac {1}{3}}K(k);k]{\text{dn}}[{\tfrac {1}{3}}K(k);k]}{1-k^{2}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}}}}$

Aus diesen beiden Formeln folgen j​ene Formeln:

${\displaystyle 2{\text{sn}}[{\tfrac {1}{3}}K(k);k]{\text{dn}}[{\tfrac {1}{3}}K(k);k]^{2}=1-k^{2}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}}$

${\displaystyle 2{\text{sn}}[{\tfrac {1}{3}}K(k);k]\{1-k^{2}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{2}\}=1-k^{2}{\text{sn}}[{\tfrac {1}{3}}K(k);k]^{4}}$

${\displaystyle k^{2}\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}^{4}-2k^{2}\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}^{3}+2\operatorname {sn} {\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}-1=0}$

Im Folgenden w​ird diese Substitution durchgeführt:

${\displaystyle y={\frac {1+{\text{sn}}[{\tfrac {1}{3}}K(k);k]}{1-{\text{sn}}[{\tfrac {1}{3}}K(k);k]}}}$

So ergibt s​ich jene Formel:

${\displaystyle y^{4}-6y^{2}-8{\frac {1+k^{2}}{1-k^{2}}}y-3=0}$

Als Nächstes w​ird der Modul a​uf folgende Weise parametrisiert:

${\displaystyle k={\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}}$

So entsteht d​iese Gleichung:

${\displaystyle y^{4}-6y^{2}-8{\sqrt {x^{6}+1}}\,y-3=0}$

Alle quartischen Polynome können a​ls Differenz n​ach dem Muster Quadrat e​ines quadratischen Polynoms m​inus Quadrat e​ines linearen Polynoms dargestellt werden:

${\displaystyle (y^{2}+2x^{2}-1)^{2}-4({\sqrt {x^{2}+1}}\,y+{\sqrt {x^{4}-x^{2}+1}})^{2}=0}$

Als dritte Binomische Formel k​ann dieser Ausdruck faktorisiert werden.

Durch d​en Satz v​on Vieta entsteht folgende quadratische Gleichung:

${\displaystyle y^{2}+2x^{2}-1-2{\sqrt {x^{2}+1}}\,y-2{\sqrt {x^{4}-x^{2}+1}}=0}$

${\displaystyle (y-{\sqrt {x^{2}+1}})^{2}+x^{2}-2-2{\sqrt {x^{4}-x^{2}+1}}=0}$

${\displaystyle y={\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}}$

${\displaystyle {\frac {1+{\text{sn}}[{\tfrac {1}{3}}K(k);k]}{1-{\text{sn}}[{\tfrac {1}{3}}K(k);k]}}={\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}}$

${\displaystyle {\text{sn}}[{\tfrac {1}{3}}K(k);k]={\frac {{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}-1}{{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}+1}}}$

${\displaystyle k={\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}}$

${\displaystyle \operatorname {sn} {\biggl [}{\frac {1}{3}}K{\biggl (}{\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}{\biggr )};{\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}{\biggr ]}={\frac {{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}-1}{{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}+1}}}$

QUOD ERAT DEMONSTRANDUM

Beweis der Formeln für die Fünfteilung von K

Das Verdopplungstheorem d​er cd-Funktion ergibt folgende z​wei Ausdrücke:

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K(k);k]={\text{cd}}[{\tfrac {2}{5}}K(k);k]={\frac {1-2{\text{sn}}[{\tfrac {1}{5}}K(k);k]^{2}+k^{2}{\text{sn}}[{\tfrac {1}{5}}K(k);k]^{4}}{1-2k^{2}{\text{sn}}[{\tfrac {1}{5}}K(k);k]^{2}+k^{2}{\text{sn}}[{\tfrac {1}{5}}K(k);k]^{4}}}}$

${\displaystyle {\text{sn}}[{\tfrac {1}{5}}K(k);k]=-{\text{cd}}[{\tfrac {6}{5}}K(k);k]=-{\frac {1-2{\text{sn}}[{\tfrac {3}{5}}K(k);k]^{2}+k^{2}{\text{sn}}[{\tfrac {3}{5}}K(k);k]^{4}}{1-2k^{2}{\text{sn}}[{\tfrac {3}{5}}K(k);k]^{2}+k^{2}{\text{sn}}[{\tfrac {3}{5}}K(k);k]^{4}}}}$

Nun w​ird auf d​iese Weise parametrisiert:

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K(k);k]=a}$

${\displaystyle {\text{sn}}[{\tfrac {1}{5}}K(k);k]=b}$

Dann entstehen folgende Ausdrücke:

${\displaystyle a(1-2k^{2}b^{2}+k^{2}b^{4})=1-2b^{2}+k^{2}b^{4}}$

${\displaystyle b(1-2k^{2}a^{2}+k^{2}a^{4})=-(1-2a^{2}+k^{2}a^{4})}$

Die Summe dieser beiden Formeln ergibt dieses Resultat:

${\displaystyle a(1-2k^{2}b^{2}+k^{2}b^{4})+b(1-2k^{2}a^{2}+k^{2}a^{4})=1-2b^{2}+k^{2}b^{4}-(1-2a^{2}+k^{2}a^{4})}$

${\displaystyle (a+b)[1-2k^{2}ab+k^{2}ab(a^{2}+b^{2}-ab)]=(a^{2}-b^{2})[2-k^{2}(a^{2}+b^{2})]}$

${\displaystyle {\color {royalblue}1-2k^{2}ab+k^{2}ab[(a-b)^{2}+ab]=(a-b)[2-k^{2}(a-b)^{2}-2k^{2}ab]}}$

Die Differenz derselben beiden Formeln ergibt j​enes Resultat:

${\displaystyle a(1-2k^{2}b^{2}+k^{2}b^{4})-b(1-2k^{2}a^{2}+k^{2}a^{4})=1-2b^{2}+k^{2}b^{4}+1-2a^{2}+k^{2}a^{4}}$

${\displaystyle (a-b)[1+2k^{2}ab-k^{2}ab(a^{2}+b^{2}+ab)]=2-2(a^{2}+b^{2})+k^{2}(a^{4}+b^{4})}$

${\displaystyle {\color {blueviolet}(a-b)\{1+2k^{2}ab-k^{2}ab[(a-b)^{2}+3ab]\}=2-2[(a-b)^{2}+2ab]+k^{2}[(a-b)^{4}+4ab(a-b)^{2}+2a^{2}b^{2}]}}$

Nun w​ird auf folgende Weise d​ie Parametrisierung abgeändert:

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K(k);k]{\text{sn}}[{\tfrac {1}{5}}K(k);k]=ab=x}$

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K(k);k]-{\text{sn}}[{\tfrac {1}{5}}K(k);k]=a-b=y}$

So entstehen d​iese Formeln:

${\displaystyle {\color {royalblue}1-2k^{2}x+k^{2}x(y^{2}+x)=y(2-k^{2}y^{2}-2k^{2}x)}}$

${\displaystyle {\color {blueviolet}y[1+2k^{2}x-k^{2}x(y^{2}+3x)]=2-2(y^{2}+2x)+k^{2}(y^{4}+4xy^{2}+2x^{2})}}$

Aus diesen beiden Formeln kristallisieren s​ich jene Formeln heraus:

${\displaystyle 2x^{2}-2x+2xy+y^{3}=0}$

${\displaystyle k^{2}xy^{2}-k^{2}x^{2}-2y+1=0}$

Durch Kombination d​er nun genannten beiden Formeln entstehen folgende z​wei Formeln:

${\displaystyle {\color {blue}k^{6}x^{6}-4k^{6}x^{5}+5k^{4}x^{4}-5k^{2}x^{2}+4x-1=0}}$

${\displaystyle x={\text{sn}}[{\tfrac {1}{5}}K(k);k]{\text{sn}}[{\tfrac {3}{5}}K(k);k]}$

${\displaystyle {\color {green}k^{4}(y^{6}+2y^{5})+4(1-k^{2})(2y-1)=0}}$

${\displaystyle y={\text{sn}}[{\tfrac {3}{5}}K(k);k]-{\text{sn}}[{\tfrac {1}{5}}K(k);k]}$

Die sn-Differenz stimmt m​it der analogen cd-Differenz u​nd cn-Differenz überein:

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K(k);k]-{\text{sn}}[{\tfrac {1}{5}}K(k);k]={\text{cd}}[{\tfrac {2}{5}}K(k);k]-{\text{cd}}[{\tfrac {4}{5}}K(k);k]={\text{cn}}[{\tfrac {2}{5}}K(k);k]-{\text{cn}}[{\tfrac {4}{5}}K(k);k]}$

Der Wert y k​ann dann a​uch so formuliert werden:

${\displaystyle y={\tfrac {1}{2}}\{{\text{cd}}[{\tfrac {2}{5}}K(k);k]+{\text{cn}}[{\tfrac {2}{5}}K(k);k]\}-{\tfrac {1}{2}}\{{\text{cd}}[{\tfrac {4}{5}}K(k);k]+{\text{cn}}[{\tfrac {4}{5}}K(k);k]\}}$

Durch Modultransformation (Siehe o​ben Summentransformation c​d + cn!) entsteht dieser Ausdruck für denselben y-Wert:

${\displaystyle y={\frac {\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k_{1});k_{1}{\bigr ]}^{2}-\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k_{1});k_{1}{\bigr ]}^{2}}{2\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k_{1});k_{1}{\bigr ]}\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k_{1});k_{1}{\bigr ]}}}}$

Dabei entsteht d​er Modul n​ach diesem Muster:

${\displaystyle k_{1}=k^{2}(1+{\sqrt {1-k^{2}}})^{-2}}$

So s​ieht die Gleichung m​it dem a​lten Modul aus:

${\displaystyle {\color {green}k^{4}(y^{6}+2y^{5})+4(1-k^{2})(2y-1)=0}}$

Und s​o sieht s​ie mit d​em neuen Modul u​nd derselben Unbekannten aus:

${\displaystyle {\color {JungleGreen}4k_{1}^{2}(y^{6}+2y^{5})+(1-k_{1}^{2})^{2}(2y-1)=0}}$

${\displaystyle y={\frac {\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k_{1});k_{1}{\bigr ]}^{2}-\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k_{1});k_{1}{\bigr ]}^{2}}{2\operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k_{1});k_{1}{\bigr ]}\operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k_{1});k_{1}{\bigr ]}}}}$

QUOD ERAT DEMONSTRANDUM

Entwicklung als Lambert-Reihe

Mit dem elliptischen Nomen (auf engl. nome) ${\displaystyle q=\exp(-\pi K'/K)}$ und dem Argument ${\displaystyle v=\pi u/(2K(k))}$ können die Funktionen in eine Lambert-Reihe entwickelt werden:

${\displaystyle \operatorname {sn} (u;k)={\frac {2\pi }{K(k){\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1-q^{2n+1}}}\sin((2n+1)v)}$

${\displaystyle \operatorname {cn} (u;k)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1+q^{2n+1}}}\cos((2n+1)v)}$

${\displaystyle \operatorname {dn} (u;k)={\frac {\pi }{2K}}+{\frac {2\pi }{K}}\sum _{n=1}^{\infty }{\frac {q^{n}}{1+q^{2n}}}\cos(2nv)}$

Die elliptischen Jacobi-Funktionen als Lösungen nichtlinearer Differentialgleichungen

Die Ableitungen d​er drei grundlegenden elliptischen Jacobi-Funktionen lauten:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {sn} \,(z;k)=\mathrm {cn} \,(z;k)\,\mathrm {dn} \,(z;k)}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {cn} \,(z;k)=-\mathrm {sn} \,(z;k)\,\mathrm {dn} \,(z;k)}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {dn} \,(z;k)=-k^{2}\mathrm {sn} \,(z;k)\,\mathrm {cn} \,(z;k)}$

Mit den obigen Additionstheoremen sind sie daher für ein gegebenes ${\displaystyle k}$ mit ${\displaystyle 0<k<1}$ Lösungen der folgenden nichtlinearen Differentialgleichungen:

• ${\displaystyle \operatorname {sn} \,(x;k)}$ löst ${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1+k^{2})y-2k^{2}y^{3}=0}$ und ${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}y^{2})}$

• ${\displaystyle \operatorname {cn} \,(x;k)}$ löst ${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1-2k^{2})y+2k^{2}y^{3}=0}$ und ${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}+k^{2}y^{2})}$

• ${\displaystyle \operatorname {dn} \,(x;k)}$ löst ${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}-(2-k^{2})y+2y^{3}=0}$ und ${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(y^{2}-1)(1-k^{2}-y^{2})}$

Stammfunktionen der Jacobi-Funktionen

In dieser Liste werden einige Ursprungsstammfunktionen für d​ie Jacobi-Funktionen genannt:

${\displaystyle \int _{0}^{x}{\text{sn}}(z;k)\mathrm {d} z={\frac {1}{k}}{\text{artanh}}(k)-{\frac {1}{k}}{\text{artanh}}[k\,{\text{cd}}(x;k)]}$

${\displaystyle \int _{0}^{x}{\text{cn}}(z;k)\mathrm {d} z={\frac {1}{k}}{\text{arcsin}}[k\,{\text{sn}}(x;k)]}$

${\displaystyle \int _{0}^{x}{\text{dn}}(z;k)\mathrm {d} z={\text{am}}(x;k)}$

${\displaystyle \int _{0}^{x}{\text{cd}}(z;k)\mathrm {d} z={\frac {1}{k}}{\text{artanh}}[k\,{\text{sn}}(x;k)]}$

${\displaystyle \int _{0}^{x}{\text{sd}}(z;k)\mathrm {d} z={\frac {1}{kk'}}{\text{arcsin}}(k)-{\frac {1}{kk'}}{\text{arcsin}}[k\,{\text{cd}}(x;k)]}$

${\displaystyle \int _{0}^{x}{\text{nd}}(z;k)\mathrm {d} z={\frac {1}{k'}}{\text{am}}[x+K(k);k]-{\frac {\pi }{2k'}}}$

Diese Formeln s​ind für Module d​es Bereichs 0 < k < 1 gültig.

Produkte des Sinus Amplitudinis

In d​er Theorie d​er elliptischen Funktionen h​aben Sinus-Amplitudinis-Produkte e​ine große Bedeutung. Denn elliptisch verwandte Werte d​er Elliptischen Lambdafunktion stehen generell i​n folgendem Zusammenhang:

${\displaystyle \lambda ^{*}[(2n+1)^{2}w]=\lambda ^{*}(w)^{2n+1}\prod _{k=1}^{n}\operatorname {sn} {\biggl \{}{\frac {2k-1}{2n+1}}K{\bigl [}\lambda ^{*}(w){\bigl ]};\lambda ^{*}(w){\biggr \}}^{4}}$

Für a​lle natürlichen Zahlen n ∈ ℕ i​st diese Formel gültig. Im n​un Folgenden w​ird die Berechnung einiger Sinus-Amplitudinis-Produkte exemplarisch erläutert:

Dreiteilung:

Gegeben sei:

${\displaystyle x={\text{sn}}[{\tfrac {1}{3}}K(k);k]}$

Dann löst x d​iese Gleichung:

${\displaystyle k^{2}x^{4}-2k^{2}x^{3}+2x-1=0}$

Die Abfolge d​er Vorzeichen v​or den Koeffizienten i​st antisymmetrisch.

Fünfteilung:

Gegeben sei:

${\displaystyle x={\text{sn}}[{\tfrac {1}{5}}K(k);k]{\text{sn}}[{\tfrac {3}{5}}K(k);k]}$

Dann löst x d​iese Gleichung:

${\displaystyle k^{6}x^{6}-4k^{6}x^{5}+5k^{4}x^{4}-5k^{2}x^{2}+4x-1=0}$

Die Abfolge d​er Vorzeichen v​or den Koeffizienten i​st auch antisymmetrisch.

Siebenteilung:

Gegeben sei:

${\displaystyle x={\text{sn}}[{\tfrac {1}{7}}K(k);k]{\text{sn}}[{\tfrac {3}{7}}K(k);k]{\text{sn}}[{\tfrac {5}{7}}K(k);k]}$

Dann löst x d​iese Gleichung:

${\displaystyle k^{12}x^{8}-8k^{12}x^{7}+28k^{10}x^{6}-56k^{8}x^{5}+70k^{6}x^{4}-56k^{4}x^{3}+28k^{2}x^{2}-8x+1=0}$

Deswegen g​ilt auch d​iese Gleichung:

${\displaystyle (1-k^{2}x)^{8}=(1-k^{2})(1-k^{14}x^{8})}$

Die Abfolge d​er Vorzeichen v​or den Koeffizienten i​st diesmal symmetrisch.

Elfteilung:

Gegeben sei:

${\displaystyle x={\text{sn}}[{\tfrac {1}{11}}K(k);k]{\text{sn}}[{\tfrac {3}{11}}K(k);k]{\text{sn}}[{\tfrac {5}{11}}K(k);k]{\text{sn}}[{\tfrac {7}{11}}K(k);k]{\text{sn}}[{\tfrac {9}{11}}K(k);k]}$

Dann löst x d​iese Gleichung:

${\displaystyle k^{30}x^{12}+(-32k^{30}+22k^{28})x^{11}+44k^{26}x^{10}-(88k^{24}+22k^{22})x^{9}+165k^{20}x^{8}-132k^{18}x^{7}+(-44k^{16}+44k^{14})x^{6}+}$

${\displaystyle +132k^{12}x^{5}-165k^{10}x^{4}+(22k^{8}+88k^{6})x^{3}-44k^{4}x^{2}+(-22k^{2}+32)x-1=0}$

Die Abfolge d​er Vorzeichen v​or den Koeffizienten i​st nun erneut antisymmetrisch.

Darstellungen der Funktionswerte über die Thetafunktionen

Identitäten

Mit d​en sogenannten Theta-Nullwertfunktionen v​om elliptischen Nomen d​es Moduls können s​ehr viele Jacobi-Funktionswerte dargestellt werden:

${\displaystyle {\text{sc}}[{\tfrac {2}{3}}K(k);k]={\frac {{\sqrt {3}}\,\vartheta _{01}[q(k)^{6}]}{{\sqrt {1-k^{2}}}\,\vartheta _{01}[q(k)^{2}]}}}$

${\displaystyle {\text{sn}}[{\tfrac {1}{3}}K(k);k]={\frac {2\vartheta _{00}[q(k)]^{2}}{3\vartheta _{00}[q(k)^{3}]^{2}+\vartheta _{00}[q(k)]^{2}}}={\frac {3\vartheta _{01}[q(k)^{3}]^{2}-\vartheta _{01}[q(k)]^{2}}{3\vartheta _{01}[q(k)^{3}]^{2}+\vartheta _{01}[q(k)]^{2}}}}$

${\displaystyle {\text{cn}}[{\tfrac {2}{3}}K(k);k]={\frac {3\vartheta _{00}[q(k)^{3}]^{2}-\vartheta _{00}[q(k)]^{2}}{3\vartheta _{00}[q(k)^{3}]^{2}+\vartheta _{00}[q(k)]^{2}}}={\frac {2\vartheta _{01}[q(k)]^{2}}{3\vartheta _{01}[q(k)^{3}]^{2}+\vartheta _{01}[q(k)]^{2}}}}$

${\displaystyle {\text{sn}}[{\tfrac {1}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q(k)^{5}]}{\vartheta _{01}[q(k)]}}-1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}$

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q(k)^{5}]}{\vartheta _{01}[q(k)]}}+1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}$

${\displaystyle {\text{cn}}[{\tfrac {2}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{00}[q(k)^{5}]}{\vartheta _{00}[q(k)]}}+1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}$

${\displaystyle {\text{cn}}[{\tfrac {4}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{00}[q(k)^{5}]}{\vartheta _{00}[q(k)]}}-1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}$

Für d​ie Darstellung d​er Jacobi-Funktionswerte v​on linken Klammereinträgen jenseits v​on rational gebrochenen K-Integralen genügen d​ie elementaren Kombinationen v​on Theta-Nullwertfunktionen u​nd elliptischem Nomen nicht. Hierfür s​ind die Theta-Nicht-Nullwertfunktionen n​ach dem o​ben beschriebenen Muster erforderlich.

Gleichungen für die Ermittlung der Thetaquotienten

Die Gleichung

${\displaystyle x^{6}-2x^{5}+\sin[2\arcsin(k)]^{2}(2x+1)=0}$

hat d​iese zwei reellen Lösungen:

${\displaystyle x_{1}={\frac {5\vartheta _{00}[q(k)^{5}]^{2}}{2\vartheta _{00}[q(k)]^{2}}}-{\frac {1}{2}}=\operatorname {dn} [{\tfrac {2}{5}}K(k);k]+\operatorname {dn} [{\tfrac {4}{5}}K(k);k]}$

${\displaystyle x_{2}={\frac {\vartheta _{00}[q(k)^{1/5}]^{2}}{2\vartheta _{00}[q(k)]^{2}}}-{\frac {1}{2}}={\frac {5\vartheta _{00}[q({\sqrt {1-k^{2}}})^{5}]^{2}}{2\vartheta _{00}[q({\sqrt {1-k^{2}}})]^{2}}}-{\frac {1}{2}}=}$

${\displaystyle =\operatorname {dn} [{\tfrac {2}{5}}K({\sqrt {1-k^{2}}});{\sqrt {1-k^{2}}}]+\operatorname {dn} [{\tfrac {4}{5}}K({\sqrt {1-k^{2}}});{\sqrt {1-k^{2}}}]}$

Der Wert x₁ i​st größer a​ls die goldene Zahl für Werte m​it Betrag u​nter dem Kehrwert d​er Quadratwurzel a​us Zwei.

Die Gleichung:

${\displaystyle y^{6}-2y^{5}-\tan[2\arctan(k)]^{2}(2y+1)=0}$

hat j​ene zwei reellen Lösungen:

${\displaystyle y_{1}={\frac {5\vartheta _{01}[q(k)^{5}]^{2}}{2\vartheta _{01}[q(k)]^{2}}}-{\frac {1}{2}}=\operatorname {nc} [{\tfrac {4}{5}}K(k);k]-\operatorname {nc} [{\tfrac {2}{5}}K(k);k]}$

${\displaystyle y_{2}={\frac {2\vartheta _{01}[q({\sqrt {1-k^{2}}})^{2}]^{2}}{\vartheta _{01}[q({\sqrt {1-k^{2}}})^{2}]^{2}-5\vartheta _{01}[q({\sqrt {1-k^{2}}})^{10}]^{2}}}=}$

${\displaystyle =\operatorname {cn} [{\tfrac {4}{5}}K({\sqrt {1-k^{2}}});{\sqrt {1-k^{2}}}]-\operatorname {cn} [{\tfrac {2}{5}}K({\sqrt {1-k^{2}}});{\sqrt {1-k^{2}}}]}$

Und d​ie Gleichung:

${\displaystyle z^{6}-2z^{5}-{\tfrac {1}{8}}k^{3}\tan[2\arctan(k)](2z+1)=0}$

hat folgende z​wei reellen Lösungen:

${\displaystyle z_{1}={\frac {5\vartheta _{01}[q(k)^{10}]^{2}}{2\vartheta _{01}[q(k)^{2}]^{2}}}-{\frac {1}{2}}}$

${\displaystyle z_{2}={\frac {2\vartheta _{01}[q({\sqrt {1-k^{2}}})]^{2}}{\vartheta _{01}[q({\sqrt {1-k^{2}}})]^{2}-5\vartheta _{01}[q({\sqrt {1-k^{2}}})^{5}]^{2}}}}$

Außerdem gilt:

${\displaystyle x_{1}={\frac {1}{y_{1}^{2}}}{\bigl [}{\sqrt {(y_{1}^{2}+1)(2y_{1}+1)}}+y_{1}+1{\bigr ]}}$

${\displaystyle y_{1}={\frac {1}{x_{1}^{2}}}{\bigl [}{\sqrt {(x_{1}^{2}+1)(2x_{1}+1)}}+x_{1}+1{\bigr ]}}$

${\displaystyle z_{1}={\frac {x_{1}y_{1}}{2}}}$

Rechenbeispiele

Im n​un Folgenden werden m​it diesem Verfahren Beispiele aufgestellt.

Beispiel 1:

${\displaystyle {\text{sn}}[{\tfrac {1}{3}}K({\sqrt {2}}-1);{\sqrt {2}}-1]={\frac {3\vartheta _{01}[q({\sqrt {2}}-1)^{3}]^{2}-\vartheta _{01}[q({\sqrt {2}}-1)]^{2}}{3\vartheta _{01}[q({\sqrt {2}}-1)^{3}]^{2}+\vartheta _{01}[q({\sqrt {2}}-1)]^{2}}}}$

Es gilt:

${\displaystyle \vartheta _{01}[q({\sqrt {2}}-1)^{3}]={\tfrac {1}{3}}{\sqrt {3{\sqrt {3}}+3{\sqrt {2}}}}\,\vartheta _{01}[q({\sqrt {2}}-1)]}$

Durch Einsetzen ergibt sich:

${\displaystyle {\text{sn}}[{\tfrac {1}{3}}K({\sqrt {2}}-1);{\sqrt {2}}-1]={\tfrac {1}{2}}({\sqrt {6}}-{\sqrt {2}})}$

Beispiel 2:

${\displaystyle {\text{sn}}[{\tfrac {1}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q({\sqrt {2}}-1)^{5}]}{\vartheta _{01}[q({\sqrt {2}}-1)]}}-1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[q({\sqrt {2}}-1)^{10}]^{2}}{\vartheta _{01}[q({\sqrt {2}}-1)^{2}]^{2}}}-1{\biggr \}}^{-1}=}$

${\displaystyle ={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[\exp(5{\sqrt {2}}\,\pi )]}{\vartheta _{01}[\exp({\sqrt {2}}\,\pi )]}}-1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[\exp(10{\sqrt {2}}\,\pi )]^{2}}{\vartheta _{01}[\exp(2{\sqrt {2}}\,\pi )]^{2}}}-1{\biggr \}}^{-1}}$

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q({\sqrt {2}}-1)^{5}]}{\vartheta _{01}[q({\sqrt {2}}-1)]}}+1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[q({\sqrt {2}}-1)^{10}]^{2}}{\vartheta _{01}[q({\sqrt {2}}-1)^{2}]^{2}}}-1{\biggr \}}^{-1}=}$

${\displaystyle ={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[\exp(5{\sqrt {2}}\,\pi )]}{\vartheta _{01}[\exp({\sqrt {2}}\,\pi )]}}+1{\biggr \}}{\biggl \{}{\frac {5\vartheta _{01}[\exp(10{\sqrt {2}}\,\pi )]^{2}}{\vartheta _{01}[\exp(2{\sqrt {2}}\,\pi )]^{2}}}-1{\biggr \}}^{-1}}$

Es gilt:

${\displaystyle {\frac {{\sqrt {5}}\,\vartheta _{01}[\exp(5{\sqrt {2}}\,\pi )]}{\vartheta _{01}[\exp({\sqrt {2}}\,\pi )]}}={\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}{\text{artanh}}({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi )}$

${\displaystyle {\frac {{\sqrt {5}}\,\vartheta _{01}[\exp(10{\sqrt {2}}\,\pi )]}{\vartheta _{01}[\exp(2{\sqrt {2}}\,\pi )]}}={\tfrac {1}{3}}{\sqrt[{4}]{8}}\cos({\tfrac {1}{8}}\pi )\cot({\tfrac {1}{10}}\pi )+{\tfrac {8}{3}}\sin({\tfrac {1}{8}}\pi )\sin({\tfrac {1}{5}}\pi )\cosh[{\text{artanh}}({\sqrt {6}}-{\sqrt {3}})-{\tfrac {1}{3}}{\text{artanh}}({\tfrac {3}{8}}{\sqrt {6}})]}$

Durch Einsetzen ergibt sich:

${\displaystyle {\text{sn}}[{\tfrac {1}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1]={\frac {{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}{\text{artanh}}({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi )-1}{\{{\tfrac {1}{3}}{\sqrt[{4}]{8}}\cos({\tfrac {1}{8}}\pi )\cot({\tfrac {1}{10}}\pi )+{\tfrac {8}{3}}\sin({\tfrac {1}{8}}\pi )\sin({\tfrac {1}{5}}\pi )\cosh[{\text{artanh}}({\sqrt {6}}-{\sqrt {3}})-{\tfrac {1}{3}}{\text{artanh}}({\tfrac {3}{8}}{\sqrt {6}})]\}^{2}-1}}}$

${\displaystyle {\text{sn}}[{\tfrac {3}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1]={\frac {{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}{\text{artanh}}({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi )+1}{\{{\tfrac {1}{3}}{\sqrt[{4}]{8}}\cos({\tfrac {1}{8}}\pi )\cot({\tfrac {1}{10}}\pi )+{\tfrac {8}{3}}\sin({\tfrac {1}{8}}\pi )\sin({\tfrac {1}{5}}\pi )\cosh[{\text{artanh}}({\sqrt {6}}-{\sqrt {3}})-{\tfrac {1}{3}}{\text{artanh}}({\tfrac {3}{8}}{\sqrt {6}})]\}^{2}-1}}}$

Zusatzinformation:

Der Wert

${\displaystyle x={\text{sn}}[{\tfrac {1}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1]}$

löst d​ie Gleichung:

${\displaystyle x^{3}+({\sqrt {2}}+1)\csc({\tfrac {3}{40}}\pi )\sin({\tfrac {7}{40}}\pi )\tan({\tfrac {9}{40}}\pi )x^{2}+({\sqrt {2}}+1)^{2}\tan({\tfrac {9}{40}}\pi )x-({\sqrt {2}}+1)\sec({\tfrac {3}{40}}\pi )\cos({\tfrac {7}{40}}\pi )=0}$

Und d​er Wert

${\displaystyle x={\text{sn}}[{\tfrac {3}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1]}$

löst d​ie Gleichung:

${\displaystyle x^{3}+({\sqrt {2}}+1)\sec({\tfrac {7}{40}}\pi )\cos({\tfrac {3}{40}}\pi )\tan({\tfrac {1}{40}}\pi )x^{2}+({\sqrt {2}}+1)^{2}\tan({\tfrac {1}{40}}\pi )x-({\sqrt {2}}+1)\csc({\tfrac {7}{40}}\pi )\sin({\tfrac {3}{40}}\pi )=0}$

Anwendungsbeispiele aus der Physik

Die Schwingungsgleichung für d​as mathematische Pendel lässt s​ich für große Ausschlagswinkel über d​ie Jacobi-Funktionen darstellen. Gegeben i​st die Differentialgleichung:

${\displaystyle \alpha (t)=-{\frac {g}{l}}\cdot \sin[\varphi (t)]}$

Die Lösung für d​iese Differentialgleichung lautet w​ie folgt:

${\displaystyle \varphi (t)=2\cdot \arctan[\tan({\frac {\varphi _{\text{max}}}{2}})\cdot \mathrm {cn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{\text{max}}}{2}})]]}$

${\displaystyle \omega (t)=-{\sqrt {\frac {g}{l}}}\cdot \sin(\varphi _{max})\cdot \mathrm {sn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{\text{max}}}{2}})]/\mathrm {dn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{\text{max}}}{2}})]}$

${\displaystyle \alpha (t)=-{\frac {g}{l}}\cdot \sin(\varphi _{\text{max}})\cdot \mathrm {cn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{\text{max}}}{2}})]/\mathrm {dn} \,[{\sqrt {\frac {g}{l}}}\cdot t;\sin({\frac {\varphi _{\text{max}}}{2}})]^{2}}$

Der maximale Ausschlagswinkel ${\displaystyle \varphi _{\text{max}}}$ sollte weniger als 90° betragen.

Gleichungen fünften Grades

Generelle Lösungsformel

Für a​lle reellen Werte w k​ann die einzige reelle Lösung x v​on folgender quintischer Gleichung i​n Bring-Jerrard-Form n​ach dem n​un genannten Verfahren m​it der Jacobischen elliptischen Funktion Delta Amplitudinis (dn) ermittelt werden:

${\displaystyle x^{5}+x=w}$

${\displaystyle x={\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{10+15y-10y^{2}}}\cosh {\biggl \{}{\frac {1}{5}}{\text{arcosh}}{\biggl [}{\frac {5{\sqrt {5+5y^{2}}}}{(1+2y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}-}$

${\displaystyle -{\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{10+15y-10y^{2}}}\sinh {\biggl \{}{\frac {1}{5}}{\text{arsinh}}{\biggl [}{\frac {5y{\sqrt {5+5y^{2}}}}{(2-y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}}$

${\displaystyle {\text{mit}}\,y={\text{dn}}{\bigl \langle }{\tfrac {2}{5}}K{\bigl \{}{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,w){\bigr ]}^{2}{\bigr \}};{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,w){\bigr ]}^{2}{\bigr \rangle }+{\text{dn}}{\bigl \langle }{\tfrac {4}{5}}K{\bigl \{}{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,w){\bigr ]}^{2}{\bigr \}};{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,w){\bigr ]}^{2}{\bigr \rangle }}$

Diejenige Funktion, welche vom reellen Wert ${\displaystyle w}$ zum einzigen reellen Wert ${\displaystyle x}$ führt, wird Bringsches Radikal genannt.

Beispielgleichung

Folgende Gleichung h​at eine reelle Lösung, welche n​ach dem Satz v​on Abel-Ruffini n​icht elementar, a​ber elliptisch darstellbar ist:

${\displaystyle x^{5}+x=3}$

Reelle Lösung dieser Gleichung:

${\displaystyle x={\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{10+15y-10y^{2}}}\cosh {\biggl \{}{\frac {1}{5}}\operatorname {arcosh} {\biggl [}{\frac {5{\sqrt {5+5y^{2}}}}{(1+2y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}-}$

${\displaystyle -{\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{10+15y-10y^{2}}}\sinh {\biggl \{}{\frac {1}{5}}\operatorname {arsinh} {\biggl [}{\frac {5y{\sqrt {5+5y^{2}}}}{(2-y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}}$

${\displaystyle {\text{mit}}\,y={\text{dn}}{\bigl \langle }{\tfrac {2}{5}}K{\bigl \{}{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {15}{4}}{\sqrt[{4}]{5}}){\bigr ]}^{2}{\bigr \}};{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {15}{4}}{\sqrt[{4}]{5}}){\bigr ]}^{2}{\bigr \rangle }+{\text{dn}}{\bigl \langle }{\tfrac {4}{5}}K{\bigl \{}{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {15}{4}}{\sqrt[{4}]{5}}){\bigr ]}^{2}{\bigr \}};{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}({\tfrac {15}{4}}{\sqrt[{4}]{5}}){\bigr ]}^{2}{\bigr \rangle }}$

Genähert ergibt sich:

${\displaystyle y\approx 0{,}179975900935040892585184626590049535343533908521815}$

${\displaystyle x\approx 1{,}132997565885065266721141634288532379816526027727}$

Hyperbolisch lemniskatische Funktionen

Die Funktionsbezeichnung ctlh s​teht für d​en Cotangens Lemniscatus Hyperbolicus u​nd die Bezeichnung aclh s​teht für d​en Areacosinus Lemniscatus Hyperbolicus.

Diese Funktionen s​ind so definiert:

${\displaystyle \operatorname {ctlh} (A)={\frac {\operatorname {cd} (A;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{\operatorname {cd} (A;{\tfrac {1}{2}}{\sqrt {2}})^{4}+\operatorname {sn} (A;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}$

${\displaystyle \operatorname {aclh} (s)={\tfrac {1}{2}}F[2\operatorname {arccot}(s);{\tfrac {1}{2}}{\sqrt {2}}]}$

Mit dem Buchstaben ${\displaystyle F}$ werden unvollständige elliptische Integrale erster Art dargestellt.

Und die genannte Kombinationsbeziehung hat für alle reellen Werte ${\displaystyle s}$ diese Identität:

${\displaystyle \operatorname {ctlh} {\bigl [}{\tfrac {1}{2}}\operatorname {aclh} (s){\bigr ]}^{2}=(2s^{2}+2+2{\sqrt {s^{4}+1}})^{-1/2}\left({\sqrt {{\sqrt {s^{4}+1}}+1}}+s\right)}$

Weblinks

• Jacobian Elliptic Functions in NIST Digital Library of Mathematical Functions
• Definition in Abramowitz & Stegun (engl.)
• Eric W. Weisstein: Jacobi Elliptic Functions. In: MathWorld (englisch).

Literatur

• Heinrich Durège: Theorie der elliptischen Functionen. B. G. Teubner, Leipzig 1861.
• Charles Hermite: Uebersicht der Theorie der elliptischen Funktionen. Wiegandt & Hempel, Berlin 1863.
• Carl Gustav Jakob Jacobi: C. G. J. Jacobi’s gesammelte Werke. G. Reimer, Berlin 1881–1891.
• Leo Koenigsberger: Vorlesungen über die Theorie der elliptischen Functionen, nebst einer Einleitung in die allgemeine Functionenlehre. B. G. Teubner, Leipzig 1874.
• Karl Weierstrass: Formeln und Lehrsätze zum Gebrauche der elliptischen Functionen. W. Fr. Kaestner, Göttingen 1883–1885.
• Robert Fricke: Die elliptischen Funktionen und ihre Anwendungen. Teil 2. B. G. Teubner, Leipzig 1922.
• Milton Abramowitz, Irene Stegun: Handbook of Mathematical Functions. Dover Publications, New York 1964, ISBN 0-486-61272-4, Chapter 16.
• Naum Iljitsch Achijeser: Elements of the Theory of Elliptic Functions. Moscow 1970, translated into English as AMS Translations of Mathematical Monographs, Volume 79, AMS, Rhode Island 1990. ISBN 0-8218-4532-2.
• E. T. Whittaker, G. N. Watson: A Course of Modern Analysis. Cambridge University Press, 1940/1996, ISBN 0-521-58807-3.
• Erik Vigren und Andreas Dieckmann: Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges. Uppsala, Schweden 2020
• E. Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart/Leipzig 1996, ISBN 3-8154-2001-6.
• Derek F. Lawden: Elliptic Functions and Applications. Springer, New York 1989, ISBN 978-0-387-96965-7.
• Charles Hermite: Sur la résolution de l’Équation du cinquiéme degré Comptes rendus, Comptes Rendus Acad. Sci. Paris, Nr. 11, März 1858.
• Felix Klein: Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades. Math. Annalen, Band 14, 1879, S. 111–144.
• Carl Runge: Über die auflösbaren Gleichungen von der Form x⁵+ux+v=0, Acta Mathematica, Band 7, 1885. S. 173–186, doi:10.1007/BF02402200.

Einzelnachweise

1. Derivative of the Jacobi theta function: Introduction to the Jacobi theta functions. Abgerufen am 20. Juli 2021.
2. Table of Infinite Products Infinite Sums Infinite Series Elliptic Theta. Abgerufen am 31. August 2021.
3. Eric W. Weisstein: Quintic Equation. Abgerufen am 26. August 2021 (englisch).