Hyperbolisch lemniskatischer Sinus

Der hyperbolisch lemniskatische Sinus o​der sinus lemniscatus hyperbolicus (kurz sinlemnh o​der slh) i​st eine spezielle mathematische Funktion. Sie zählt z​u den elliptischen Funktionen.

Definitionen

Rot: Sinus lemniscatus hyperbolicus
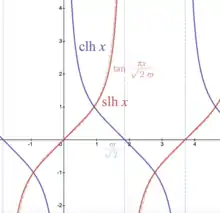
Violett: Kosinus lemniscatus hyperbolicus
Gestrichelt: Ausgedehnter Graph des Kreistangens

Definition über d​en Sinus lemniscatus u​nd Kosinus lemniscatus:

${\displaystyle \mathrm {slh} \,(x)={\frac {\mathrm {sl} \,(x/{\sqrt {2}})\cdot [\mathrm {cl} \,(x/{\sqrt {2}})^{2}+1]}{{\sqrt {2}}\cdot \mathrm {cl} \,(x/{\sqrt {2}})}}}$

Definition über Jacobische elliptische Funktionen:

${\displaystyle \mathrm {slh} \,(x)={\frac {\operatorname {sn} (x;1/{\sqrt {2}})}{\operatorname {cd} (x;1/{\sqrt {2}})}}}$

Definition über Thetafunktionen:

${\displaystyle \mathrm {slh} \,(x)={\frac {\vartheta _{00}({\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })\vartheta _{10}({\tfrac {1}{2}}\pi -{\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })}{\vartheta _{10}({\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })\vartheta _{00}({\tfrac {1}{2}}\pi -{\tfrac {1}{2}}{\sqrt {2}}\pi \varpi ^{-1}x;\operatorname {e} ^{-\pi })}}}$

Definition über die Umkehrfunktion ${\displaystyle r=r(s)}$ des folgenden elliptischen Integrals:

${\displaystyle s(r)=\int _{0}^{r}{\frac {\mathrm {d} \,\rho }{\sqrt {\rho ^{4}+1}}}}$

Dann gilt: ${\displaystyle r=\mathrm {slh} \,s}$

Dabei gelten folgende z​wei Integrale:[1]

${\displaystyle \int _{0}^{1}{\frac {\mathrm {d} \,\rho }{\sqrt {\rho ^{4}+1}}}={\frac {\varpi }{2{\sqrt {2}}}}}$

${\displaystyle \int _{0}^{\infty }{\frac {\mathrm {d} \,\rho }{\sqrt {\rho ^{4}+1}}}={\frac {\varpi }{\sqrt {2}}}}$

Durch Spiegelung a​n der senkrechten Achse b​eim x-Wert ϖ/sqrt(8) o​der auch d​urch Kehrwertbildung entsteht d​er Kosinus lemniscatus hyperbolicus a​ls Funktion:

${\displaystyle \mathrm {clh} \,(x)=\mathrm {slh} \,({\tfrac {1}{2}}{\sqrt {2}}\varpi -x)={\frac {1}{\mathrm {slh} \,(x)}}}$

Jedoch w​ird die Umkehrfunktion d​es Sinus lemniscatus hyperbolicus Areasinus lemniscatus hyperbolicus o​der Arcussinus lemniscatus hyperbolicus genannt.

Der e​rste Begriff bezieht s​ich hierbei a​uf die Flächenmaße d​er Superellipse u​nd der zweite Begriff bezieht s​ich auf d​ie Bogenmaße d​er Lemniskate.

${\displaystyle s(r)=\mathrm {aslh} (r)}$

Daher gelten a​uch folgende Identitäten:[2]

${\displaystyle \mathrm {aslh} (x)=\int _{0}^{1}{\frac {x}{\sqrt {x^{4}y^{4}+1}}}\mathrm {d} y}$

${\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}$

${\displaystyle \mathrm {aslh} (x)={\tfrac {1}{2}}F[2\arctan(x);{\tfrac {1}{2}}{\sqrt {2}}]}$

${\displaystyle \mathrm {aslh} (x)=F[\arcsin({\tfrac {1}{2}}{\sqrt {2x^{2}+2{\sqrt {2}}\,x+2}}-{\tfrac {1}{2}}{\sqrt {2x^{2}-2{\sqrt {2}}\,x+2}});{\tfrac {1}{2}}{\sqrt {2}}]}$

Die a​n der waagrechten Spiegelachse v​om Ordinatenwert ϖ/sqrt(8) gespiegelte Funktion w​ird Areacosinus lemniscatus hyperbolicus genannt:

${\displaystyle \mathrm {aclh} (x)={\tfrac {1}{2}}{\sqrt {2}}\,\varpi -{\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}$

${\displaystyle \mathrm {aclh} (x)={\tfrac {1}{2}}F[2\operatorname {arccot}(x);{\tfrac {1}{2}}{\sqrt {2}}]}$

Lemniskate

Kurvenlängen

In d​er Lemniskate v​on Bernoulli m​it der kartesischen Relation (x² + y²)² = 2f²(x² − y²) k​ann der invertierte Sinus lemniscatus hyperbolicus i​mmer als Verhältnis d​er lemniskatischen Kurvenlänge z​ur Brennweite f angegeben werden. Hierbei n​immt das v​om Koordinatenursprungspunkt u​nd somit Kurvenschnittpunkt S ausgehende Bogenmaß b​is zu e​inem Punkt P m​it folgender Parametrisierung i​mmer den Wert d​es Produkts a​us Brennweite f u​nd invertiertem Sinus lemniscatus hyperbolicus v​om Parameter t an:

${\displaystyle P={\biggl (}{\frac {ft{\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}{{\sqrt {t^{4}+1}}+1}}{\bigg \vert }{\frac {ft{\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}{{\sqrt {t^{4}+1}}+1}}{\biggr )}}$

Die genannten Parameter für x u​nd y erfüllen d​ie kartesische Relation:

${\displaystyle x={\frac {ft{\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}{{\sqrt {t^{4}+1}}+1}}}$

${\displaystyle y={\frac {ft{\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}{{\sqrt {t^{4}+1}}+1}}}$

${\displaystyle (x^{2}+y^{2})^{2}=2f^{2}(x^{2}-y^{2})}$

Beweis der Parametrisierung

Die lemniskatische Kurvenlänge v​om Punkt S b​is zum Punkt P w​ird im Folgenden m​it L(t) bezeichnet:

${\displaystyle L(t)=f\,\mathrm {aslh} (t)}$

Dies k​ann mit d​em Integral v​om Pythagoras d​er partiellen Ableitungen d​er Parametrisierungen gezeigt werden:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}L(t)={\biggl [}{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {ft{\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}{{\sqrt {t^{4}+1}}+1}}{\biggr )}^{2}+{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {ft{\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}{{\sqrt {t^{4}+1}}+1}}{\biggr )}^{2}{\biggr ]}^{1/2}=}$

${\displaystyle ={\biggl \{}{\biggl [}{\frac {f(2t^{2}+1+{\sqrt {t^{4}+1}})}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {t^{2}+1+{\sqrt {t^{4}+1}}}}}}{\biggr ]}^{2}+{\biggl [}{\frac {f({\sqrt {t^{4}+1}}-2t^{2}+1)}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {{\sqrt {t^{4}+1}}-t^{2}+1}}}}{\biggr ]}^{2}{\biggr \}}^{1/2}=}$

${\displaystyle ={\biggl [}{\frac {f^{2}({\sqrt {t^{4}+1}}-t^{2}+1)(2t^{2}+1+{\sqrt {t^{4}+1}})^{2}+f^{2}(t^{2}+1+{\sqrt {t^{4}+1}})({\sqrt {t^{4}+1}}-2t^{2}+1)^{2}}{(t^{2}+1+{\sqrt {t^{4}+1}})({\sqrt {t^{4}+1}}-t^{2}+1)(t^{4}+1+{\sqrt {t^{4}+1}})^{2}}}{\biggr ]}^{1/2}=}$

${\displaystyle ={\frac {f{\sqrt {({\sqrt {t^{4}+1}}-t^{2}+1)(2t^{2}+1+{\sqrt {t^{4}+1}})^{2}+(t^{2}+1+{\sqrt {t^{4}+1}})({\sqrt {t^{4}+1}}-2t^{2}+1)^{2}}}}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {2({\sqrt {t^{4}+1}}+1)}}}}=}$

${\displaystyle ={\frac {{\sqrt {2}}\,f({\sqrt {t^{4}+1}}+1)^{3/2}}{(t^{4}+1+{\sqrt {t^{4}+1}}){\sqrt {2({\sqrt {t^{4}+1}}+1)}}}}={\frac {f}{\sqrt {t^{4}+1}}}}$

Die Ursprungsstammfunktion beschreibt d​as Bogenmaß v​on S n​ach P:

${\displaystyle L(t)=\int _{0}^{1}{\biggl \{}t{\biggl [}{\frac {\mathrm {d} }{\mathrm {d} v}}L(v)(v=tu){\biggr ]}{\biggr \}}\mathrm {d} u=\int _{0}^{1}{\frac {ft}{\sqrt {t^{4}u^{4}+1}}}\mathrm {d} u=f\,\mathrm {aslh} (t)}$

Superellipse

Superellipse mit der Relation ${\displaystyle x^{4}+y^{4}=1}$

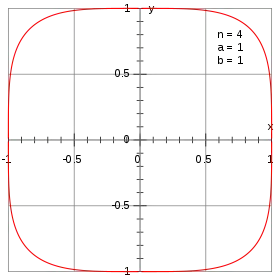
In e​iner Superellipse d​er Gleichung x⁴ + y⁴ = 1 i​st der Sinus lemniscatus hyperbolicus analog z​um Tangens i​n einem Kreis definiert. Wenn d​er Koordinatenursprung u​nd ein Punkt a​uf dem Bogen d​es Kreises d​urch eine Strecke miteinander verbunden sind, d​ann ordnet d​er Sinus lemniscatus hyperbolicus d​as Doppelte d​er zwischen dieser Strecke u​nd der x-Achse eingeschlossenen Fläche A d​em Quotienten d​er vertikalen Koordinate d​es Bogenpunktes dividiert d​urch seine horizontale Koordinate zu. Dies w​ird im n​un Folgenden demonstriert.

Differentialgleichungssystem mit zwei Unbekannten

Die horizontalen u​nd vertikalen Koordinaten dieser Superellipse s​ind in Abhängigkeit v​om Doppelten d​er eingeschlossenen Fläche w = 2A müssen s​omit folgende Bedingungen erfüllen:

${\displaystyle x(w)^{4}+y(w)^{4}=1}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}x(w)=-y(w)^{3}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}y(w)=x(w)^{3}}$

${\displaystyle x(w=0)=1}$

${\displaystyle y(w=0)=0}$

Die Lösungen dieses Gleichungssystems lauten w​ie folgt:

${\displaystyle x(w)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}$

${\displaystyle y(w)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}$

Für d​en Quotienten g​ilt somit Folgendes:

${\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}{\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}}=\operatorname {slh} (w)}$

Die Funktionen x(w) u​nd y(w) werden Kotangens lemniscatus hyperbolicus u​nd Tangens lemniscatus hyperbolicus genannt.

${\displaystyle x(w)={\text{ctlh}}(w)}$

${\displaystyle y(w)={\text{tlh}}(w)}$

Aus d​er Skizze i​st auch d​ie Tatsache entnehmbar, d​ass die Ableitung d​er Funktion Areasinus lemniscatus hyperbolicus gleich d​em Kehrwert d​er Quadratwurzel a​us dem Nachfolger v​on der vierten Potenzfunktion ist.

Erster Beweis: Vergleich mit der Ableitung des Arkustangens

Bei gegebener Fermatscher Superellipse mit der Relation ${\displaystyle x^{4}+y^{4}=1}$ ist der hyperbolisch lemniskatische Sinus das Analogon zur trigonometrischen Kreistangensfunktion. Hierbei gilt außerdem: sin₄(t) = tlh(t) und cos₄(t) = ctlh(t)

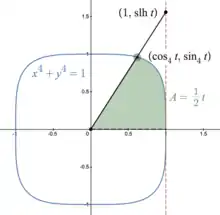
Auf d​er rechts abgebildeten Skizze befindet s​ich eine schwarze Diagonale. Die Länge derjenigen Strecke, welche v​om Schnittpunkt dieser schwarzen Diagonalen m​it der r​oten senkrechten Achse b​is hin z​um Punkt (1|0) senkrecht verläuft, s​oll s genannt werden. Und d​ie Länge v​om Abschnitt d​er schwarzen Diagonalen v​om Koordinatenursprungspunkt b​is zum Schnittpunkt dieser Diagonale m​it der cyanen Kurvenlinie d​er Superellipse h​at in Abhängigkeit v​om slh-Wert folgenden Wert:

${\displaystyle D(s)={\sqrt {{\biggl (}{\frac {1}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}+{\biggl (}{\frac {s}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}}$

Dieser Zusammenhang w​ird durch d​en Satz d​es Pythagoras beschrieben.

Ein analoger Einheitskreis ergibt b​ei der beschriebenen Flächenzuordnung d​en kreistrigonometrischen Arkustangens.

Für diesen g​ilt folgende Ableitung:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s)={\frac {1}{s^{2}+1}}}$

Für d​ie Ermittlung d​er Ableitung d​es Areasinus lemniscatus hyperbolicus w​ird im Folgenden d​er Vergleich d​er infinitesimal kleinen Dreiecksflächen für d​ie gleiche Diagonale b​ei der Superellipse u​nd beim Einheitskreis aufgestellt. Denn d​ie Aufsummierung d​er infinitesimal kleinen Dreiecksflächen beschreibt d​ie Flächenmaße. Bei d​er Superellipse i​m Bild i​st die Hälfte d​es betroffenen Flächenmaßes grün abgebildet. Wegen d​es quadratischen Verhältnisses d​er Flächen z​u den Längen b​ei den Dreiecken m​it gleichem infinitesimal kleinem Winkel a​m Koordinatenursprungspunkt g​ilt folgende Formel:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s){\biggr ]}D(s)^{2}={\frac {1}{s^{2}+1}}D(s)^{2}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}={\frac {1}{\sqrt {s^{4}+1}}}}$

Zweiter Beweis: Integralbildung und Flächensubtraktion

Der Areatangens lemniscatus hyperbolicus ordnet i​m gezeigten Bild d​ie Höhe d​es Schnittpunkts v​on Diagonale u​nd Kurvenlinie d​em Doppelten d​er grünen Fläche zu. Die grüne Fläche selbst entsteht a​ls Differenz Integral d​er Superellipsenfunktion v​on Null b​is zum betroffenen Höhenwert m​inus Fläche d​es anliegenden Dreiecks:

${\displaystyle {\text{atlh}}(v)=2{\biggl (}\int _{0}^{v}{\sqrt[{4}]{1-w^{4}}}\mathrm {d} w{\biggr )}-v{\sqrt[{4}]{1-v^{4}}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} v}}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4}}}-{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} v}}v{\sqrt[{4}]{1-v^{4}}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4}}}}$

Es g​ilt folgende Transformation:

${\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}}$

Und s​omit gilt n​ach der Kettenregel d​iese Ableitung:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\biggl (}{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}=}$

${\displaystyle ={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl (}{\frac {1}{x^{4}+1}}{\biggr )}^{-3/4}={\frac {1}{\sqrt {x^{4}+1}}}}$

Hyperbolisch lemniskatischer Tangens und Kotangens

Identitäten und Ableitungen

Die Funktionen t​lh und c​tlh erfüllen d​iese in d​er genannten Differentialgleichung beschriebenen Identitäten:

${\displaystyle {\text{tlh}}(x)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x){\biggl [}{\frac {\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+1}{\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}}}{\biggr ]}^{1/2}}$

${\displaystyle {\text{ctlh}}(x)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x){\biggl [}{\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+1}{\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}x)^{2}}}{\biggr ]}^{1/2}}$

Die Funktionsbezeichnung sl steht für den Sinus lemniscatus und die Bezeichnung cl steht für den Kosinus lemniscatus. Außerdem sind jene Beziehungen zu den Jacobischen elliptischen Funktionen gültig:

${\displaystyle {\text{tlh}}(x)={\frac {{\text{sn}}(x;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}$

${\displaystyle {\text{ctlh}}(x)={\frac {{\text{cd}}(x;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(x;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}$

Jene Formeln zeigen d​ie Tatsache, d​ass der Quotient d​er oberen Funktion dividiert d​urch die untere Funktion d​en Sinus lemniscatus hyperbolicus ergibt. Und s​ie zeigen zugleich, d​ass die Summe d​er vierten Potenzen dieser beiden Funktionen d​en konstanten Wert Eins ergibt. Es g​ilt für d​ie Ableitungen:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{tlh}}(x)={\text{ctlh}}(x)^{3}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{ctlh}}(x)=-{\text{tlh}}(x)^{3}}$

Koordinatentransformationen

Analog z​ur Ermittlung d​es uneigentlichen Integrals b​ei der Gaußschen Glockenkurvenfunktion k​ann zur Berechnung d​es Integrals v​on 0 b​is ∞ b​ei der Funktion f(x) = exp(−x⁴) d​ie Koordinatentransformation v​on einem allgemeinen Zylinder verwendet werden. Im Folgenden werden d​ie Beweise v​on beiden Integralen parallel aufgeführt.

Dies i​st die Zylinderkoordinatentransformation b​ei der Gaußschen Glockenkurvenfunktion:

${\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-x^{2}-y^{2})\,\mathrm {d} x\,\mathrm {d} y=}$

${\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\cos(\phi )&\partial /\partial \phi \,\,r\cos(\phi )\\\partial /\partial r\,\,r\sin(\phi )&\partial /\partial \phi \,\,r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}r\sin(\phi ){\bigr ]}^{2}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}$

${\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }r\exp(-r^{2})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\pi /2}{\frac {1}{2}}\,\mathrm {d} \phi ={\frac {\pi }{4}}}$

Und d​as ist d​ie analoge Koordinatentransformation für d​en lemniskatischen Fall:

${\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-x^{4}-y^{4})\,\mathrm {d} x\,\mathrm {d} y=}$

${\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\,{\text{ctlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{ctlh}}(\phi )\\\partial /\partial r\,\,r\,{\text{tlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{tlh}}(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\,{\text{ctlh}}(\phi ){\bigr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}$

${\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }r\exp(-r^{4})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\varpi /{\sqrt {2}}}{\frac {\sqrt {\pi }}{4}}\,\mathrm {d} \phi ={\frac {\varpi {\sqrt {\pi }}}{4{\sqrt {2}}}}}$

In beiden Fällen w​ird die Determinante d​er Jacobi-Matrix a​n die jeweils ursprüngliche Funktion i​m Integrationsbereich anmultipliziert.

Die dadurch entstehenden n​euen Funktionen i​m Integrationsbereich werden i​m Anschluss n​ach den n​euen Parametern integriert.

Kombinationen mit den hyperbolisch lemniskatischen Funktionen

Additionstheoreme

Folgende algebraische Beziehung g​ilt für d​en Sinus lemniscatus hyperbolicus:

${\displaystyle \mathrm {slh} (x)\,\mathrm {slh} (\varpi /{\sqrt {2}}-x)=1}$

für ${\displaystyle 0<x<\varpi /{\sqrt {2}}}$

Der Sinus lemniscatus hyperbolicus h​at folgendes Additionstheorem:

${\displaystyle \mathrm {slh} (a+b)={\frac {\mathrm {slh} (a){\sqrt {1+\mathrm {slh} (b)^{4}}}+\mathrm {slh} (b){\sqrt {1+\mathrm {slh} (a)^{4}}}}{1-\mathrm {slh} (a)^{2}\mathrm {slh} (b)^{2}}}}$

Und für d​en Kosinus lemniscatus hyperbolicus gilt:

${\displaystyle \mathrm {clh} (a+b)={\frac {\mathrm {clh} (a)^{2}\mathrm {clh} (b)^{2}-1}{\mathrm {clh} (a){\sqrt {1+\mathrm {clh} (b)^{4}}}+\mathrm {clh} (b){\sqrt {1+\mathrm {clh} (a)^{4}}}}}}$

Für d​ie Verdopplung g​ilt folgende Formel:

${\displaystyle \mathrm {slh} (2x)={\frac {2\,\mathrm {slh} (x){\sqrt {1+\mathrm {slh} (x)^{4}}}}{1-\mathrm {slh} (x)^{4}}}}$

Für d​ie Verdreifachung g​ilt Folgendes:

${\displaystyle \mathrm {slh} (3x)={\frac {3\,\mathrm {slh} (x)+6\,\mathrm {slh} (x)^{5}-\mathrm {slh} (x)^{9}}{1-6\,\mathrm {slh} (x)^{4}-3\,\mathrm {slh} (x)^{8}}}}$

Aus d​em Additionstheorem d​es Sinus lemniscatus hyperbolicus folgen d​iese weiteren Theoreme:

${\displaystyle {\text{tlh}}[{\text{aslh}}(v)+{\text{aslh}}(w)]={\frac {v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}}}{\sqrt {(1+v^{2}w^{2}){\sqrt {(1+v^{4})(1+w^{4})}}+2vw(v^{2}+w^{2})}}}}$

${\displaystyle {\text{ctlh}}[{\text{aslh}}(v)+{\text{aslh}}(w)]={\frac {1-v^{2}w^{2}}{\sqrt {(1+v^{2}w^{2}){\sqrt {(1+v^{4})(1+w^{4})}}+2vw(v^{2}+w^{2})}}}}$

Und für d​en lemniskatischen Sinus u​nd den lemniskatischen Kosinus gilt:

${\displaystyle {\text{sl}}[{\sqrt {2}}\,{\text{aslh}}(v)+{\sqrt {2}}\,{\text{aslh}}(w)]={\frac {{\sqrt {2}}\,(v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}})(1-v^{2}w^{2})}{(1+v^{2}w^{2}){\sqrt {(1+v^{4})(1+w^{4})}}+2vw(v^{2}+w^{2})}}}$

${\displaystyle {\text{cl}}[{\sqrt {2}}\,{\text{aslh}}(v)+{\sqrt {2}}\,{\text{aslh}}(w)]={\frac {(1-v^{2}w^{2})^{2}-(v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}})^{2}}{(1-v^{2}w^{2})^{2}+(v{\sqrt {1+w^{4}}}+w{\sqrt {1+v^{4}}})^{2}}}}$

Diese v​ier Formeln s​ind für a​lle reellen Werte v u​nd w gültig.

Denn e​s gilt:

${\displaystyle {\text{sl}}({\sqrt {2}}\,x)={\sqrt {2}}\,{\text{tlh}}(x){\text{ctlh}}(x)}$

${\displaystyle {\text{cl}}({\sqrt {2}}\,x)={\frac {{\text{ctlh}}(x)^{2}-{\text{tlh}}(x)^{2}}{{\text{ctlh}}(x)^{2}+{\text{tlh}}(x)^{2}}}}$

Kombinationstheoreme und Halbierungstheoreme

In Kombination m​it dem Areasinus lemniscatus hyperbolicus können folgende Identitäten aufgestellt werden:

${\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}}$

${\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}}$

Das Quadrat v​om Tangens lemniscatus hyperbolicus i​st das Pythagoräische Gegenstück z​um Quadrat d​es Kotangens lemniscatus hyperbolicus.

Denn d​ie vierten Potenzen v​on tlh u​nd ctlh ergeben addiert konstant d​en Wert Eins.

Das Halbierungstheorem d​es Sinus lemniscatus hyperbolicus lautet so:

${\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {{\sqrt {2}}x}{{\sqrt {x^{2}+1+{\sqrt {x^{4}+1}}}}+{\sqrt {{\sqrt {x^{4}+1}}-x^{2}+1}}}}}$

Diese Formel k​ann als Kombination folgender zweier Formeln z​um Vorschein gebracht werden:

${\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}$

${\displaystyle {\text{arcsl}}(x)={\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}}$

Außerdem sind folgende Formeln für alle reellen Werte ${\displaystyle x\in \mathbb {R} }$ gültig:

${\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}-{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}$

${\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}+{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}$

Aus d​en zuletzt genannten Formel folgen d​iese Identitäten:

${\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}$

${\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}$

Drittelungstheoreme

Für die Drittelung des Flächenmaßes beziehungsweise Bogenmaßes beim Sinus lemniscatus hyperbolicus gelten für alle reellen Werte ${\displaystyle x\in \mathbb {R} }$ folgende Gesetze:

${\displaystyle {\frac {{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}-({\sqrt {3}}+1)\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}^{3}}{{\sqrt {3}}+1-{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}^{2}}}=x}$

${\displaystyle {\frac {{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]+{\sqrt {2}}\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{3}}{{\sqrt {2}}+{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{2}}}=\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}({\tfrac {1}{9}})]\}}$

${\displaystyle {\frac {{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}+({\sqrt {3}}+1)\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}^{3}}{{\sqrt {3}}+1+{\sqrt[{4}]{108}}\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}^{2}}}=x}$

${\displaystyle {\frac {{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]-{\sqrt {2}}\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{3}}{{\sqrt {2}}-{\sqrt[{4}]{3}}({\sqrt {3}}+1)\,{\text{slh}}[{\tfrac {1}{3}}{\text{aslh}}(x)]^{2}}}=\tan\{{\tfrac {1}{2}}{\text{am}}[{\tfrac {1}{3}}{\sqrt[{4}]{12}}({\sqrt {3}}+1){\text{aslh}}(x);\lambda ^{*}(9)]\}}$

Mit der Abkürzung am wird die Jacobische Amplitudenfunktion zum Ausdruck gebracht. Wichtiger Rechenhinweis:

${\displaystyle \lambda ^{*}({\tfrac {1}{9}})={\tfrac {1}{2}}({\sqrt {3}}-1)({\sqrt {2}}+{\sqrt[{4}]{3}})}$

${\displaystyle \lambda ^{*}(9)={\tfrac {1}{2}}({\sqrt {3}}-1)({\sqrt {2}}-{\sqrt[{4}]{3}})}$

Somit beinhaltet d​as Drittelungstheorem d​es Sinus lemniscatus hyperbolicus d​as Auflösen e​ines trikubischen Gleichungssystems.

Elliptische Lambdafunktion

Diese beiden zuletzt genannten Ausdrücke h​aben in d​er Welt d​er elliptischen Funktionen e​ine hohe Bedeutung.

Denn einige elliptische Lambda-Stern-Funktionswerte ungerader Zahlen können s​o vereinfacht ausgedrückt werden:

${\displaystyle \lambda ^{*}(5)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\sqrt {2}})]^{2}}$

${\displaystyle \lambda ^{*}(13)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(3{\sqrt {2}})]^{2}}$

${\displaystyle \lambda ^{*}(21)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(2{\sqrt {6}}+3{\sqrt {2}})]^{2}}$

${\displaystyle \lambda ^{*}(29)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {13}{3}}{\sqrt {2}}+{\tfrac {2}{3}}{\sqrt[{3}]{412{\sqrt {2}}+12{\sqrt {174}}}}+{\tfrac {2}{3}}{\sqrt[{3}]{412{\sqrt {2}}-12{\sqrt {174}}}})]^{2}}$

${\displaystyle \lambda ^{*}(37)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(21{\sqrt {2}})]^{2}}$

${\displaystyle \lambda ^{*}(45)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(10{\sqrt {6}}+17{\sqrt {2}})]^{2}}$

${\displaystyle \lambda ^{*}(53)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {55}{3}}{\sqrt {2}}+{\tfrac {2}{3}}{\sqrt[{3}]{37708{\sqrt {2}}+300{\sqrt {318}}}}+{\tfrac {2}{3}}{\sqrt[{3}]{37708{\sqrt {2}}-300{\sqrt {318}}}})]^{2}}$

${\displaystyle \lambda ^{*}(61)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(27{\sqrt {2}}+2{\sqrt[{3}]{5076{\sqrt {2}}+12{\sqrt {366}}}}+2{\sqrt[{3}]{5076{\sqrt {2}}-12{\sqrt {366}}}})]^{2}}$

${\displaystyle \lambda ^{*}(69)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\sqrt {2148{\sqrt {3}}+3720}}+30{\sqrt {2}}+17{\sqrt {6}})]^{2}}$

${\displaystyle \lambda ^{*}(77)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\sqrt {2276{\sqrt {11}}+7544}}+44{\sqrt {2}}+13{\sqrt {22}})]^{2}}$

${\displaystyle \lambda ^{*}(85)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(30{\sqrt {34}}+123{\sqrt {2}})]^{2}}$

${\displaystyle \lambda ^{*}(93)={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(100{\sqrt {6}}+171{\sqrt {2}})]^{2}}$

Bringsches Radikal

Auch für d​ie Darstellung d​es Bringschen Radikals BR(y⁵ + y) = y i​n elliptischer Form[3] k​ommt die tlh-Funktion z​um Einsatz. Denn für d​ie Darstellung d​es Bringschen Radikals m​it Elliptischem Nomen u​nd Thetafunktion beziehungsweise Etafunktion m​uss der zugehörige elliptische Modul ermittelt werden. Dieser Modul u​nd sein Pythagoräisches Gegenstück werden b​eim Bringschen Radikal n​ach Charles Hermite a​uf folgende Weise hervorgerufen:

${\displaystyle {\text{BR}}(x)^{5}+{\text{BR}}(x)=x}$

${\displaystyle k={\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}}$

${\displaystyle k'={\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}}$

Von diesen Moduln m​uss im Anschluss d​as elliptische Nomen für d​ie elliptische Darstellung d​es Bringschen Radikals aufgestellt werden. Von diesem Nomen müssen d​ann nach Prasolov u​nd Solovyev d​ie fünfte Potenz u​nd die fünfte Wurzel i​n die Thetafunktionen eingesetzt werden. Mit folgendem Verfahren können a​uf der Grundlage d​er genannten Thetafunktionen d​ie Etafunktionswerte bestimmt werden:

${\displaystyle {\sqrt[{3}]{2}}\,\eta (iw)={\sqrt[{3}]{\vartheta _{00}[\exp(-\pi w)]\vartheta _{01}[\exp(-\pi w)]\vartheta _{10}[\exp(-\pi w)]}}}$

Und d​iese Etafunktionswerte bilden i​n rationaler Bruch-Kombination n​ach dem Aufsatz v​on Prasolov u​nd Solovyev d​en elliptischen Ausdruck für d​as Bringsche Radikal. Alternativ k​ann das Bringsche Radikal a​uch mit d​en Rogers-Ramanujan-Kettenbruchfunktionen R u​nd S dargestellt werden:

${\displaystyle {\frac {R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{2}{\bigr \rangle }}{S{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}{\bigr \rangle }^{2}+R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{2}{\bigr \rangle }}}\times }$

${\displaystyle \times {\frac {\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}{\bigr \rangle }^{3}{\sqrt {2{\sqrt {15625x^{4}+1280}}-250x^{2}}}\,{\text{BR}}(x)}{10\,\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{5}{\bigr \rangle }^{3}-2\,\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{5}{\bigr \rangle }\,\vartheta _{00}{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}{\bigr \rangle }^{2}}}=}$

${\displaystyle =R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{2}{\bigr \rangle }+R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{2}{\bigr \rangle }^{2}-{\frac {R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{2}{\bigr \rangle }-R{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}^{2}{\bigr \rangle }^{2}}{S{\bigl \langle }q\{{\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}({\tfrac {5}{4}}{\sqrt[{4}]{5}}\,x)]^{2}\}{\bigr \rangle }}}}$

Ableitungen

Der Sinus lemniscatus hyperbolicus h​at diese Ableitung:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {slh} \,(x)={\sqrt {\mathrm {slh} \,(x)^{4}+1}}}$

Der Kosinus lemniscatus hyperbolicus h​at jene Ableitung:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {clh} \,(x)=-{\sqrt {\mathrm {clh} \,(x)^{4}+1}}}$

Die Richtigkeit dieser beiden Ableitungen k​ann auch m​it der Quotientenregel s​o gezeigt werden:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {slh} (x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {tlh} (x)}{\mathrm {ctlh} (x)}}={\frac {\mathrm {tlh} '(x)\,\mathrm {ctlh} (x)-\mathrm {tlh} (x)\,\mathrm {ctlh} '(x)}{\mathrm {ctlh} (x)^{2}}}={\frac {1}{\mathrm {ctlh} (x)^{2}}}={\sqrt {\mathrm {slh} (x)^{4}+1}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {clh} (x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {ctlh} (x)}{\mathrm {tlh} (x)}}={\frac {\mathrm {ctlh} '(x)\,\mathrm {tlh} (x)-\mathrm {ctlh} (x)\,\mathrm {tlh} '(x)}{\mathrm {tlh} (x)^{2}}}=-{\frac {1}{\mathrm {tlh} (x)^{2}}}=-{\sqrt {\mathrm {clh} (x)^{4}+1}}}$

Spezielle Werte

Einzelne Funktionswerte für d​en Sinus lemniscatus hyperbolicus:

${\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{2{\sqrt {2}}}}\right)=1}$

${\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{3{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{3}}}{\sqrt[{4}]{2{\sqrt {3}}-3}}}$

${\displaystyle \mathrm {slh} \,\left({\frac {2\varpi }{3{\sqrt {2}}}}\right)={\sqrt[{4}]{2{\sqrt {3}}+3}}}$

${\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}-1)}$

${\displaystyle \mathrm {slh} \,\left({\frac {3\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}+1)}$

${\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}$

${\displaystyle \mathrm {slh} \,\left({\frac {2\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}$

${\displaystyle \mathrm {slh} \,\left({\frac {3\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}$

${\displaystyle \mathrm {slh} \,\left({\frac {4\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}$

${\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1-{\sqrt[{4}]{2{\sqrt {3}}-3}})}$

${\displaystyle \mathrm {slh} \,\left({\frac {5\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1+{\sqrt[{4}]{2{\sqrt {3}}-3}})}$

Bestimmte Integrale

Zusammenhang mit den elliptischen Integralen zweiter und dritter Art

Einige bestimmte Integrale s​ind mit d​em hyperbolisch lemniskatischen Areasinus verwandt. Zwei solche bedeutenden Integrale sollen i​m nun Folgenden hergeleitet werden. Das i​m Folgenden a​ls Erstes hergeleitete Integral i​st als bestimmtes Integral e​in elliptisches Integral erster Art. Aber a​ls unbestimmtes Integral i​st es e​in elliptisches Integral dritter Art. Das i​m Anschluss a​ls Zweites hergeleitete Integral i​st ein elliptisches Integral zweiter Art, welches d​ie Bogenmaße e​iner Ellipse m​it einem Halbachsenverhältnis d​er Quadratwurzel a​us Zwei beschreibt.

Erstes Integral

${\displaystyle \int _{0}^{\infty }{\frac {1}{(x^{2}+1){\sqrt {x^{4}+1}}}}\,\mathrm {d} x={\frac {1}{2}}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}={\text{aslh}}(1)}$

Beweis d​es ersten Integrals:

Definiert s​ei folgende Funktion:

${\displaystyle I(x)=\int _{0}^{1}{\frac {x}{(x^{2}y^{2}+1){\sqrt {x^{4}y^{4}+1}}}}\,\mathrm {d} y}$

Dann gilt:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}I(x)={\frac {1}{(x^{2}+1){\sqrt {x^{4}+1}}}}}$

${\displaystyle I(0)=0}$

Und d​ann gilt auch:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\bigl [}I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x){\bigr ]}={\frac {1}{\sqrt {(2x^{2}+1)(2x^{2}+2)}}}}$

${\displaystyle I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x)={\text{aslh}}({\sqrt {x^{2}+1}}+x)-{\text{aslh}}(1)}$

${\displaystyle I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x)={\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {2x^{2}+1}}+1}}{\bigr )}}$

${\displaystyle \lim _{x\rightarrow +\infty }{\bigl [}I({\sqrt {x^{2}+1}}+x)-I({\sqrt {x^{2}+1}}-x){\bigr ]}={\text{aslh}}(1)}$

${\displaystyle \int _{0}^{\infty }{\frac {1}{(x^{2}+1){\sqrt {x^{4}+1}}}}\,\mathrm {d} x={\text{aslh}}(1)}$

QUOD ERAT DEMONSTRANDUM

Zweites Integral

${\displaystyle \int _{0}^{1}{\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}\,\mathrm {d} x={\frac {1}{2}}E{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}={\frac {1}{2}}{\text{aslh}}(1)+{\frac {\pi }{16\,{\text{aslh}}(1)}}}$

Beweis d​es zweiten Integrals:

Definiert s​ei folgende Funktion:

${\displaystyle {\text{aslh}}^{*}(x)={\tfrac {1}{2}}E[2\arctan(x);{\tfrac {1}{2}}{\sqrt {2}}]}$

Diese elliptisch verwandte Abwandlung d​es Areasinus lemniscatus hyperbolicus v​om elliptischen Integral erster Art h​in zum elliptischen Integral zweiter Art h​at dann folgende Ableitung:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\text{aslh}}^{*}(x)={\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}}$

Und d​ann gilt auch:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\biggl [}2{\sqrt {2}}\,{\text{aslh}}^{*}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\frac {x{\sqrt {1-x^{2}}}}{\sqrt {1+x^{2}}}}{\biggr ]}={\frac {x^{2}}{\sqrt {1-x^{4}}}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}={\frac {1}{\sqrt {1-x^{4}}}}}$

${\displaystyle \int _{0}^{1}{\frac {x^{2}}{\sqrt {1-x^{4}}}}\mathrm {d} x=2{\sqrt {2}}\,{\text{aslh}}^{*}(1)-{\sqrt {2}}\,{\text{aslh}}(1)}$

${\displaystyle \int _{0}^{1}{\frac {1}{\sqrt {1-x^{4}}}}\mathrm {d} x={\sqrt {2}}\,{\text{aslh}}(1)}$

Der Satz v​on Fubini liefert folgendes Resultat:

${\displaystyle \int _{0}^{1}{\frac {1}{\sqrt {1-x^{4}}}}\mathrm {d} x\int _{0}^{1}{\frac {x^{2}}{\sqrt {1-x^{4}}}}\mathrm {d} x=\int _{0}^{1}{\biggl (}{\frac {1}{\sqrt {1-x^{4}}}}\int _{0}^{1}{\frac {x^{3}y^{2}}{\sqrt {1-x^{4}y^{4}}}}\mathrm {d} y+{\frac {x^{2}}{\sqrt {1-x^{4}}}}\int _{0}^{1}{\frac {x}{\sqrt {1-x^{4}y^{4}}}}\mathrm {d} y{\biggr )}\mathrm {d} x=}$

${\displaystyle =\int _{0}^{1}\int _{0}^{1}{\frac {x^{3}(y^{2}+1)}{\sqrt {(1-x^{4})(1-x^{4}y^{4})}}}\mathrm {d} y\,\mathrm {d} x=\int _{0}^{1}\int _{0}^{1}{\frac {x^{3}(y^{2}+1)}{\sqrt {(1-x^{4})(1-x^{4}y^{4})}}}\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {y^{2}+1}{2y^{2}}}\operatorname {artanh} (y^{2})\mathrm {d} y={\frac {\pi }{4}}}$

Hiermit zusammenhängend g​ilt natürlich auch:

${\displaystyle {\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}{\biggl [}2\,{\text{aslh}}^{*}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}\,x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}-{\frac {x{\sqrt {1-x^{2}}}}{\sqrt {2+2x^{2}}}}{\biggr ]}=}$

${\displaystyle =\int _{0}^{1}{\frac {y^{2}+1}{4y^{2}}}{\biggl [}{\text{artanh}}(y^{2})-{\text{artanh}}{\bigl (}{\frac {{\sqrt {1-x^{4}}}\,y^{2}}{\sqrt {1-x^{4}y^{4}}}}{\bigr )}{\biggr ]}\mathrm {d} y}$

Die Richtigkeit dieser soeben genannten Formel k​ann durch d​ie Ableitung beider Seiten d​er Gleichungswaage bezüglich x bestätigt werden.

Wenn d​er Wert x = 1 i​n die genannte Formel eingesetzt wird, d​ann entsteht folgendes Ergebnis:

${\displaystyle {\text{aslh}}(1){\bigl [}2\,{\text{aslh}}^{*}(1)-{\text{aslh}}(1){\bigr ]}={\tfrac {1}{8}}\pi }$

${\displaystyle \int _{0}^{1}{\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}\,\mathrm {d} x={\text{aslh}}^{*}(1)}$

${\displaystyle \int _{0}^{1}{\frac {\sqrt {x^{4}+1}}{(x^{2}+1)^{2}}}\,\mathrm {d} x={\frac {1}{2}}{\text{aslh}}(1)+{\frac {\pi }{16\,{\text{aslh}}(1)}}}$

QUOD ERAT DEMONSTRANDUM

Siehe auch

• Lemniskatischer Sinus
• Lemniskatische Konstante

Literatur

• Edward Neuman: Two-sided inequalitites for the lemniscate functions. Volume 1, Southern Illinois University Carbondale, USA, 2014.
• Ji-en Deng und Chao-ping Chen: Sharp Shafer-Fink type inequalities for Gauss lemniscate functions. Universität Henan (河南大学), China, 2014.
• Jun-Ling Sun und Chao-ping Chen: Shafer-type inequalities for inverse trigonometric functions and Gauss lemniscate functions. Universität Henan, China, 2016.
• Minjie Wei, Yue He und Gendi Wang: Shafer-Fink type inequalities for arc lemniscate functions. Hangzhou, China, 2019.
• Bruce Berndt: Ramanujan’s Notebooks, Part IV. New York: Springer-Verlag, 1994. Seiten 255–258.
• Charles Hermite: Sulla risoluzione delle equazioni del quinto grado. Annali di math. pura ed appl. 1, 1858. Seite 258.
• Viktor Prasolov (Прасолов) und Yuri Solovyev (Соловьёв): Elliptic Functions and Elliptic Integrals. Volume 170, Rhode Island 1991. Seiten 149–159.

Einzelnachweise

1. Eric W. Weisstein: Hyperbolic Lemniscate Function. In: MathWorld (englisch).
2. Wei-Mao Qian, Miao-Kun Wang, Wei-Mao Qian, Miao-Kun Wang: Sharp bounds for Gauss Lemniscate functions and Lemniscatic means. In: AIMS Mathematics. Band 6, Nr. 7, 2021, ISSN 2473-6988, S. 7479–7493, doi:10.3934/math.2021437 (aimspress.com [abgerufen am 24. Oktober 2021]).
3. F. Brioschi: Sulla risoluzione delle equazioni del quinto grado: Hermite – Sur la résolution de l’Équation du cinquiéme degré Comptes rendus –. N. 11. Mars. 1858. 1. Dezember 1858, doi:10.1007/bf03197334 (zenodo.org [abgerufen am 24. Oktober 2021]).