Sekans hyperbolicus und Kosekans hyperbolicus

Die Funktionen Kosekans hyperbolicus (csch) u​nd Sekans hyperbolicus (sech) s​ind Hyperbelfunktionen. Sie ergeben s​ich als Kehrwert v​on Sinus hyperbolicus bzw. Kosinus hyperbolicus.

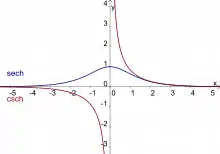
Sekans hyperbolicus (blau) und Kosekans hyperbolicus (rot)

Definitionen

${\displaystyle {\begin{aligned}\operatorname {sech} \ x&={\frac {2}{e^{x}+e^{-x}}}={\frac {1}{\cosh x}}\\\operatorname {csch} \ x&={\frac {2}{e^{x}-e^{-x}}}={\frac {1}{\sinh x}}\end{aligned}}}$

Eigenschaften

	Sekans hyperbolicus	Kosekans hyperbolicus
Definitionsbereich	${\displaystyle -\infty <x<+\infty }$	${\displaystyle -\infty <x<+\infty \,;\,x\neq 0}$
Wertebereich	${\displaystyle 0<f(x)\leq 1}$	${\displaystyle -\infty <f(x)<+\infty \,;\,f(x)\neq 0}$
Periodizität	keine	keine
Monotonie	${\displaystyle x<0}$ streng monoton steigend ${\displaystyle x>0}$ streng monoton fallend	${\displaystyle x>0}$ streng monoton fallend ${\displaystyle x<0}$ streng monoton fallend
Symmetrien	Spiegelsymmetrie zur y-Achse	Punktsymmetrie zum Koordinatenursprung Achsensymmetrie zu ${\displaystyle y=-x}$
Asymptote	${\displaystyle f(x)\to 0}$ für ${\displaystyle x\to \pm \infty }$	${\displaystyle f(x)\to 0}$ für ${\displaystyle x\to \pm \infty }$
Nullstellen	keine	keine
Sprungstellen	keine	keine
Polstellen	keine	${\displaystyle x=0}$
Extrema	Maximum bei ${\displaystyle x=0}$	keine
Wendepunkte	${\displaystyle x=\pm \ln {(1+{\sqrt {2}})}}$	keine

Umkehrfunktionen

Die Umkehrfunktion s​ind die entsprechenden Areafunktionen:

${\displaystyle {\begin{aligned}x&=\operatorname {arsech} \ y\\x&=\operatorname {arcsch} \ y\end{aligned}}}$

Ableitungen

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sech} \ x&=-\operatorname {sech} \ x\cdot \operatorname {tanh} \ x=-{\frac {\sinh x}{\cosh ^{2}x}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {csch} \ x&=-\operatorname {csch} \ x\cdot \operatorname {coth} \ x=-{\frac {\cosh x}{\sinh ^{2}x}}=-\operatorname {csch} \ x\cdot {\sqrt {1+\operatorname {csch} ^{2}x}}\\\end{aligned}}}$

Integrale

${\displaystyle {\begin{aligned}\int \operatorname {sech} x\ \mathrm {d} x&=\arctan \left(\sinh x\right)+C\\\int \operatorname {csch} x\ \mathrm {d} x&=\ln \left|\operatorname {tanh} \,{\frac {x}{2}}\right|+C\end{aligned}}}$

Die d​urch den Koordinatenursprung verlaufende Stammfunktion d​es Sekans hyperbolicus w​ird Gudermannfunktion genannt.

Reihenentwicklungen

${\displaystyle {\begin{aligned}\operatorname {sech} \ x&=\sum _{k=0}^{\infty }(-1)^{k}{\frac {(8k+4)\pi }{(2k+1)^{2}\pi ^{2}+4x^{2}}}\\\operatorname {csch} \ x&=1/x+\sum _{k=1}^{\infty }(-1)^{k}{\frac {2x}{k^{2}\pi ^{2}+x^{2}}}\end{aligned}}}$

Komplexes Argument

${\displaystyle {\begin{aligned}&\operatorname {sech} (x+\mathrm {i} y)={\frac {2\cosh(x)\cos(y)}{\cosh(2x)+\cos(2y)}}+\mathrm {i} {\frac {-2\sinh(x)\sin(y)}{\cosh(2x)+\cos(2y)}}\\&\operatorname {sech} (\mathrm {i} y)=\sec(y)\\&\operatorname {csch} (x+\mathrm {i} y)={\frac {2\sinh(x)\cos(y)}{\cosh(2x)-\cos(2y)}}+\mathrm {i} \;{\frac {-2\cosh(x)\sin(y)}{\cosh(2x)-\cos(2y)}}\\&\operatorname {csch} (\mathrm {i} y)=-\mathrm {i} \csc(y)\end{aligned}}}$

Siehe auch

• Trigonometrische Funktionen
• Kreis- und Hyperbelfunktionen.

Weblinks

• Eric W. Weisstein: Hyperbolic Cosecant. In: MathWorld (englisch).