Syllogismus

Die Syllogismen (von altgriechisch συλλογισμός syllogismós „[das] Zusammenrechnen“, „logischer Schluss“) sind ein Katalog bestimmter Typen logischer Schlüsse. Sie bilden den Kern der im vierten Jahrhundert vor unserer Zeitrechnung entstandenen antiken Logik des Aristoteles und der traditionellen Logik bis ins 19. Jahrhundert. Als Haupttechnik der Logik abgelöst wurde der syllogistische Ansatz erst durch die Integration der Logik in die Mathematik, im Gefolge der Arbeiten von George Boole und Gottlob Frege im 19. und frühen 20. Jahrhundert.

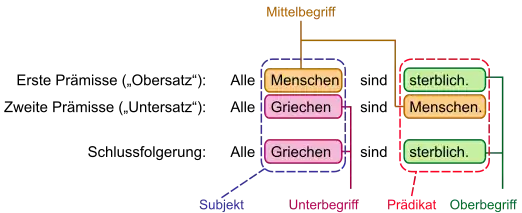
Beispiel für einen gültigen Syllogismus

Als Syllogistik wird allgemein die Lehre von den Syllogismen bezeichnet. Die klassische Logik untersuchte insbesondere, unter welchen Voraussetzungen Syllogismen gültig sind. Syllogismen sind immer nach dem gleichen Muster aufgebaut. Jeweils zwei Prämissen (Voraussetzungen), Obersatz und Untersatz genannt, führen zu einer Konklusion (Schlussfolgerung). Die Prämissen und die Konklusion sind Aussagen von einem bestimmten Typ, in denen jeweils einem Begriff, dem syllogistischen Subjekt, ein anderer Begriff, das syllogistische Prädikat (nicht gleichbedeutend mit Subjekt und Prädikat in der Grammatik), in bestimmter Weise zu- oder abgesprochen wird. In Abhängigkeit von der Stelle, an der sie im Syllogismus auftreten, werden die vorkommenden Begriffe Oberbegriff, Mittelbegriff und Unterbegriff genannt.

Geschichte

Der lateinische Begriff syllogismus geht auf das griechische syllogismos (συλλογισμός) zurück. Mit syllogismos bezeichnet Aristoteles ein deduktives Argument, das er als erster folgendermaßen definiert:

„Eine Deduktion (syllogismos) ist also ein Argument, in welchem sich, wenn etwas gesetzt wurde, etwas anderes als das Gesetzte mit Notwendigkeit durch das Gesetzte ergibt.“

– Aristoteles: Topik I 1, 100a25-27[1]

In diesem weiteren Sinn, also als Synonym für das Wort „Argument“, wurde das Wort „Syllogismus“ alltagssprachlich bis ins 20. Jahrhundert hinein verwendet.[2] Im modernen Sprachgebrauch ist diese weite Verwendung nicht mehr üblich und nur mehr in Ausdrücken wie hypothetischer Syllogismus (ein Sammelbegriff für bestimmte in der Tradition betrachtete aussagenlogische Schlussweisen) anzutreffen.

Syllogismus bezeichnet verwirrenderweise traditionell nun ausschließlich eine spezielle Form des deduktiven Arguments (syllogismos), nämlich die in Aristoteles’ Erster Analytik behandelte Deduktion, die aus genau zwei Prämissen, einer Konklusion und drei Begriffen besteht. Da die Definition der Deduktion diese Einschränkung nicht aufweist, ist zwar jeder Syllogismus ein syllogismos, aber nicht jeder syllogismos ein Syllogismus.

Nach der Position des Mittelbegriffs – das heißt desjenigen Begriffs, der nur in den Prämissen vorkommt – unterscheidet Aristoteles drei Arten von Schlüssen, Figuren genannt (siehe Abschnitt Figuren). Die Einführung einer vierten Figur, deren Schlüsse auch Aristoteles schon als gültig anerkennt,[3] wird von Avicenna und anderen Galen zugeschrieben, obwohl es für diese Zuschreibung keine direkten Hinweise im überlieferten Werk Galens gibt[4] und dieser sie in der Tat sogar ausdrücklich ablehnt.[5] Bis zur Einführung der vierten Figur werden ihre Syllogismen in der Tradition des Theophrastos von Eresos oft der ersten Figur zugerechnet.

Im lateinischen Mittelalter, das die logischen Werke des Aristoteles zunächst aus Übersetzungen und Kommentaren des Boëthius aufnahm, wurden die traditionellen lateinischen Bezeichnungen für Quantität und Qualität der Urteile (siehe Abschnitt Typen von Aussagen) durch Petrus Hispanus gebräuchlich.[6] In der Scholastik erhielt die Syllogistik die Form, die dann jahrhundertelang in den Lehrbüchern tradiert wurde, wobei der authentische Gehalt der aristotelischen Syllogistik schon seit der Antike verloren gegangen war und sie seit der Renaissance zunehmend scharfer Kritik unterzogen wurde (berühmt ist etwa die Kritik von René Descartes). Erst Jan Łukasiewicz hat Aristoteles' Logik in einer bahnbrechenden Arbeit[7] neu entdeckt und sie vom Standpunkt der modernen Logik aus axiomatisch rekonstruiert; unter anderem wegen der hohen Zahl der dabei angesetzten Axiome wird jedoch bezweifelt, dass diese Rekonstruktion ausreichend gegenstandsadäquat ausgefallen ist.[8] An Łukasiewicz schließt die neuere Forschung an, die ihr deutschsprachiges Standardwerk in Günther Patzigs Darstellung[9] (1959) gefunden hat.

Seither unterscheidet man zwischen der aristotelischen und der traditionellen Syllogistik. Der auffälligste äußere Unterschied besteht darin, dass Aristoteles Syllogismen nicht als eine Folge von drei Sätzen niederschreibt, sondern als einen Satz der Form „Wenn (Prämisse 1) und (Prämisse 2), so notwendig (Konklusion)“; es besteht Uneinigkeit darüber, ob sich diese Formulierung als metasprachliche Aussage über einen Syllogismus im traditionellen Verständnis erklären lasse[10] oder ob der Sicht Łukasiewicz zu folgen sei, dass Aristoteles einen Syllogismus als eine zusammengesetzte Aussage betrachte. Die beiden Lesarten lassen sich einfach ineinander überführen; der vorliegende Artikel gibt konkrete Syllogismen im Sinn der ersteren Lesart durchgängig als Folge von drei Sätzen wieder. Auch von diesem strittigen Punkt abgesehen gibt es zwischen der aristotelischen und der traditionellen Syllogistik zahlreiche Unterschiede in der logisch-semantischen Auffassung, so dass heute vielfach die Ansicht vertreten wird, Aristoteles stehe der modernen Logik im Grunde viel näher als der traditionellen Syllogistik. Bereits auf Augustus De Morgan geht die unter anderem von Patzig ausgearbeitete Auffassung der aristotelischen Syllogistik als Theorie bestimmter zweistelliger Relationen zwischen Begriffen sowie des relativen Produktes solcher Relationen zurück.[11] Ein Syllogismus ist dann ein Relationenprodukt, das selbst wieder eine Relation in jener bestimmten Form ist, die in den vier Satztypen A, E, I oder O ausgedrückt wird (zu A, E, I, O siehe Typen von Aussagen).

Die unterschiedslose Gleichsetzung von aristotelischer und traditioneller Syllogistik in der älteren Geschichtsschreibung der Logik (Carl Prantl, Heinrich Maier) hat hingegen zahlreiche Irrtümer – etwa über die angeblichen metaphysischen Voraussetzungen von Aristoteles' Logik – hervorgebracht, von denen sich die Aristotelesinterpretation nur mit Mühe befreien konnte.

Allgemeine Darstellung

Syllogistische Argumente sind immer nach dem gleichen Muster aufgebaut. Jeweils zwei Prämissen (Voraussetzungen), genannt Obersatz (lateinisch propositio major) und Untersatz (lateinisch propositio minor), führen zu einer Konklusion (Schlussfolgerung, lateinisch conclusio). Im hier dargestellten kategorischen Syllogismus (auch assertorischer Syllogismus genannt) sind Prämissen und Konklusion kategorische Urteile, d. h. Aussagen, in denen einem Begriff (griechisch ὅρος – horos, lateinisch terminus), dem Subjekt, ein anderer Begriff, das Prädikat, in bestimmter Weise zu- oder abgesprochen wird. Zum Beispiel wird im kategorischen Urteil „Alle Menschen sind sterblich“ dem Subjekt „Mensch“ das Prädikat „sterblich“ zugesprochen. Zu beachten – und an diesem Beispiel ersichtlich – ist, dass die Wörter „Subjekt“ und „Prädikat“ im Zusammenhang der Syllogistik anders verwendet werden als in der traditionellen Grammatik, wo das grammatikalische Subjekt der Ausdruck „alle Menschen“ und das grammatikalische Prädikat – je nach Sichtweise – das Wort „sind“[12] oder der Ausdruck „sind sterblich“[13] wäre.

Innerhalb eines Syllogismus werden insgesamt drei verschiedene Begriffe verwendet:

der Oberbegriff (lateinisch terminus major), der im Obersatz und auf der rechten Seite der Konklusion, d. h. als deren Prädikat (P) vorkommt;
der Unterbegriff (lateinisch terminus minor), der im Untersatz und auf der linken Seite der Konklusion, d. h. als deren Subjekt (S) vorkommt; und
der Mittelbegriff (M) (lateinisch terminus medius), der im Obersatz und im Untersatz, nicht aber in der Konklusion vorkommt.

In der Nachfolge von Johannes Philoponus wird den Bezeichnungen „Oberbegriff“ und „Unterbegriff“ seit dem 17. Jahrhundert mehrheitlich keinerlei inhaltliche Bedeutung beigemessen und sie werden ausschließlich aus ihrem Auftreten im Obersatz beziehungsweise im Untersatz und als Prädikat beziehungsweise Subjekt der Konklusion erklärt.[14] Gelegentlich werden Unter- und Oberbegriff auch als Subjekt bzw. Prädikat des Syllogismus bezeichnet.

Ein Beispiel für einen gültigen Syllogismus ist Folgendes:

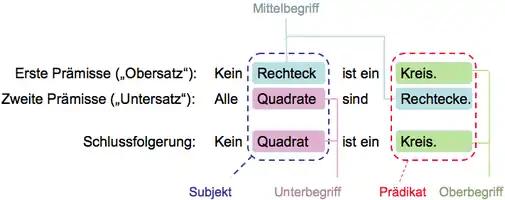
Kein Rechteck ist ein Kreis. Alle Quadrate sind Rechtecke. Also ist kein Quadrat ein Kreis.

Der Mittelbegriff dieses Syllogismus ist der Begriff „Rechteck“; im Obersatz dieses Syllogismus tritt der Mittelbegriff als Subjekt, in seinem Untersatz als Prädikat auf. Der Unterbegriff dieses Syllogismus ist der Begriff „Quadrat“; er tritt im Untersatz als Subjekt auf. Der Oberbegriff dieses Syllogismus ist schließlich der Begriff „Kreis“; er tritt im Obersatz als Prädikat auf.

Alternativ zu Formulierungen wie „Kein S ist P“ oder „Alle S sind P“ werden auch gleichbedeutende Ausdrücke wie „P kommt keinem S zu“ und „P kommt allem S zu“ verwendet. In dieser Ausdrucksweise lautet der obige Syllogismus wie folgt:

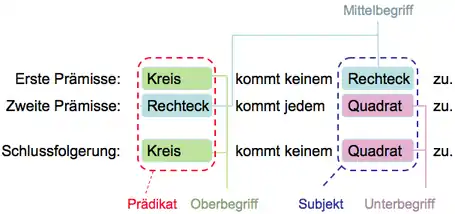
Kreis kommt keinem Rechteck zu. Rechteck kommt allem Quadrat zu. Also kommt Kreis keinem Quadrat zu.

Die beiden Schreibweisen sind gleichbedeutend und gleichwertig. Während Aristoteles selber in seinen Analytiken überwiegend Varianten der zweiten Formulierung, „P kommt allem S zu“, wählt (meist „τὁ P κατηγορεῖται τοῦ S“ – „das P wird über das S ausgesagt“), wird seit der Scholastik Varianten der ersten Schreibweise, „Alle S sind P“, der Vorzug gegeben. Stärker als in der traditionellen tritt in der aristotelischen Formulierung der Unterschied zwischen grammatikalischem und syllogistischem Subjekt bzw. Prädikat zutage; so hat in der Formulierung „P kommt allem S zu“ das syllogistische Prädikat, „P“, die Funktion des grammatikalischen Subjekts und das syllogistische Subjekt, „S“, die Funktion des grammatikalischen Prädikats.

Es gibt jedoch in der Nachfolge von Jan Łukasiewicz die Meinung, dass die aristotelischen Syllogismen im Gegensatz zu denen der sich auf ihn berufenden Tradition keine Argumente aus zwei Prämissen und einer Konklusion seien, sondern zusammengesetzte Einzelsätze. Aus dieser Sicht müsse die aristotelische Variante des obigen Beispiels wie folgt lauten:

Wenn kein Rechteck ein Kreis ist und alle Quadrate Rechtecke sind, dann ist kein Quadrat ein Kreis.

Die richtige Einordnung der aristotelischen Syllogismen ist bis heute strittig. Da die Umwandlung zwischen den beiden Lesarten einfach ist und da Aristoteles seine Syllogismen trotz ihrer Formulierung in „Wenn–dann“-Form als Schlussregeln gebraucht,[15] stellt der vorliegende Artikel konkrete Syllogismen durchgängig in ihrer traditionellen Formulierung als aus drei Aussagen zusammengesetzte Argumente dar.

Als Weiterentwicklung der kategorischen oder assertorischen Syllogistik gibt es schon bei Aristoteles Ansätze einer modalen Syllogistik, bei der in den – von diesem Unterschied abgesehen gleich aufgebauten – Syllogismen modale Aussagen wie „Alle Menschen sind möglicherweise sterblich“ zugelassen sind.

Logische Systeme, die wie die Syllogistik mit Aussagen arbeiten, in denen Begriffe zueinander in Beziehung gesetzt werden, werden allgemein Begriffslogiken genannt.

Typen von Aussagen

Eine Aussage in einem Syllogismus, ein kategorisches Urteil, setzt immer zwei Begriffe in eine Beziehung. Dabei werden nur vier Typen von Urteilen bezüglich der Beziehung zwischen einem Subjekt (S) und einem Prädikat (P) betrachtet:

Typ

Bezeichnung

Formulierungen des Urteils

Kurzschreibweise

A

allgemein bejahendes Urteil

alle S sind P (und es gibt tatsächlich S)

P kommt allem S zu

SaP

E

allgemein verneinendes Urteil

kein S ist P (und es gibt tatsächlich S)

P kommt keinem S zu

SeP

I

partikulär bejahendes Urteil

einige S sind P

P kommt einigem S zu

SiP

O

partikulär verneinendes Urteil

einige S sind nicht P

P kommt einigem S nicht zu

SoP

Die Vokale stammen dabei aus den lateinischen Worten „affirmo“ (ich bejahe) und „nego“ (ich verneine), wobei jeweils der erste Vokal für ein allgemeines, der zweite für ein partikuläres Urteil steht.

Quantität und Qualität

Die Eigenschaft einer Aussage, über wie viele Gegenstände sie spricht, wird traditionell die Quantität dieser Aussage genannt. In diesem Sinn gibt es im Syllogismus zwei Quantitäten, nämlich (a) partikulär und (b) universell oder allgemein. Die Eigenschaft einer Aussage, einem Subjekt ein Prädikat zu- oder abzusprechen, wird traditionell die Qualität dieser Aussage genannt. Spricht eine Aussage einem Subjekt ein Prädikat zu, nennt man sie bejahende Aussage, spricht sie es ihm ab, verneinende Aussage. Die Typen von Aussagen sind in folgender Tabelle nach ihrer Qualität und Quantität aufgeschlüsselt:

	bejahend	verneinend
allgemein	A-Urteil	E-Urteil
partikulär	I-Urteil	O-Urteil

Logisches Quadrat

Das logische Quadrat

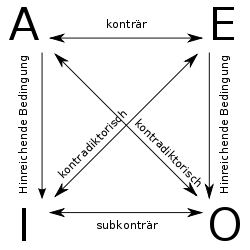
Unter der Voraussetzung, dass ihre Subjekte keine leeren Begriffe sind, bestehen zwischen den unterschiedlichen Aussagentypen verschiedene Beziehungen:

Zwei Aussagen bilden einen kontradiktorischen Gegensatz genau dann, wenn beide weder gleichzeitig wahr noch gleichzeitig falsch sein können, mit anderen Worten: Wenn beide unterschiedliche Wahrheitswerte haben müssen. Das wiederum ist genau dann der Fall, wenn die eine Aussage die Negation der anderen ist (und umgekehrt). Für die syllogistischen Aussagentypen trifft das kontradiktorische Verhältnis auf die Paare A–O und I–E zu.
Zwei Aussagen bilden einen konträren Gegensatz genau dann, wenn sie zwar nicht beide zugleich wahr, wohl aber beide falsch sein können. In der Syllogistik steht nur das Aussagenpaar A–E in konträrem Gegensatz.
Zwei Aussagen bilden einen subkonträren Gegensatz genau dann, wenn nicht beide zugleich falsch (wohl aber beide zugleich wahr) sein können. In der Syllogistik steht nur das Aussagenpaar I–O in subkonträrem Gegensatz.
Zwischen den Aussagetypen A und I einerseits und E und O andererseits besteht ein Folgerungszusammenhang (traditionell wird dieser Folgerungszusammenhang im logischen Quadrat Subalternation genannt): Aus A folgt I, d. h., wenn alle S P sind, dann gibt es auch tatsächlich S, die P sind; und aus E folgt O, d. h., wenn keine S P sind, dann gibt es tatsächlich S, die nicht P sind.

Diese Zusammenhänge werden oft in einem Schema, das unter dem Namen „Logisches Quadrat“ bekannt wurde, zusammengefasst (siehe Abbildung). Die älteste bekannte Niederschrift des logischen Quadrats stammt aus dem zweiten nachchristlichen Jahrhundert und wird Apuleius von Madauros zugeschrieben.[16]

Existenzielle Voraussetzungen

Wie schon im logischen Quadrat ersichtlich, gelten viele der überlieferten Gesetzmäßigkeiten der Syllogistik nur unter der Voraussetzung, dass zumindest das Subjekt der betroffenen Aussagen nicht leer ist. Im Allgemeinen wird daher davon ausgegangen, dass syllogistische Aussagen tatsächlich Existenzaussagen über das Subjekt treffen, d. h. voraussetzen, dass das Subjekt kein leerer Begriff ist:

Die Aussage „Alle S sind P“ bedeutet damit: „Es gibt S, und alle davon sind P“.
Die Aussage „Keine S sind P“ bedeutet damit: „Es gibt S, und keine davon sind P“.
Die Aussage „Einige S sind P“ bedeutet damit: „Es gibt S, und einige von ihnen sind P.“
Die Aussage „Einige S sind nicht P“ bedeutet damit: „Es gibt S, und einige von ihnen sind nicht P.“

Die Existenzaussage „Es gibt S“ wird dabei für gewöhnlich nicht als Teil des jeweiligen syllogistischen Urteils verstanden, sondern als seine Präsupposition, das heißt als Voraussetzung dafür, dass das jeweilige Urteil zum syllogistischen Schließen überhaupt verwendet werden kann. Die Existenzaussage zum Teil des syllogistischen Urteils zu machen ist zwar möglich, aber formal relativ kompliziert, und wird hinsichtlich seiner Adäquatheit unterschiedlich beurteilt.[17]

Je nach Interpretation der syllogistischen Aussagen und Gesetzmäßigkeiten ist auch die Sicht möglich, dass syllogistisches Schließen überhaupt nur mit nicht leeren Begriffen möglich sei, das heißt, dass auch die Prädikate nicht leer sein dürfen.[18] Die Frage, welche Autoren der Tradition welche Sichtweise vertreten haben, wird unterschiedlich beurteilt und ist bis heute Gegenstand philosophischer und philologischer Untersuchungen.

Obwohl existenzielle Voraussetzungen dem natürlichen Sprachgebrauch entsprechen (normalerweise empfindet man nur Allaussagen über tatsächlich vorhandene Dinge als sinnvoll), ist es wichtig, sich ihrer bewusst zu sein, weil es durchaus auch logische Systeme gibt, die diese Voraussetzungen nicht machen.

Distribution

In der Syllogistik wird von der Distribution (von lateinisch distributio, Verteilung) eines Begriffs innerhalb einer Aussage gesprochen. Ein Begriff ist innerhalb einer Aussage genau dann distribuiert, wenn aus dieser Aussage jede andere Aussage folgt, die aus der ursprünglichen Aussage entsteht, indem der ursprüngliche Begriff durch einen echten Unterbegriff ersetzt wird.[19] Eine oft gebrauchte und bei richtigem Verständnis äquivalente Formulierung lautet: Ein Begriff ist innerhalb einer syllogistischen Aussage genau dann distribuiert, wenn er sich innerhalb der Aussage auf alle Gegenstände bezieht, auf die der Begriff zutrifft.

Zum Beispiel ist in der syllogistischen A-Aussage „Alle Philosophen (Subjekt) sind Menschen (Prädikat)“ der Begriff „Philosoph“ distribuiert: Aus der Tatsache, dass alle Philosophen Menschen sind, folgt, dass alle Sprachphilosophen (ein Unterbegriff von „Philosoph“) Menschen sind, dass alle Existenzphilosophen (ein weiterer Unterbegriff von „Philosoph“) Menschen sind usw. Nicht distribuiert ist in dieser Aussage hingegen der Begriff „Mensch“: Aus der Tatsache, dass alle Philosophen Menschen sind, folgt zum Beispiel noch lange nicht, dass alle Philosophen Europäer (ein Unterbegriff von Mensch) sind.

Eine Übersicht darüber, in welchem Typ von Aussage welcher Begriff distribuiert ist, gibt die folgende Tabelle.

	Subjekt	Prädikat
A-Urteil	distribuiert	nicht distribuiert
E-Urteil	distribuiert	distribuiert
I-Urteil	nicht distribuiert	nicht distribuiert
O-Urteil	nicht distribuiert	distribuiert

Syllogismen aus moderner Sicht

Es gibt verschiedene Ansätze, die traditionelle Syllogistik zu axiomatisieren bzw. auf eindeutigen Regeln aufzubauen.

Die klassischen Syllogismen lassen sich modern sowohl als Anwendung eines Teilsystems der Prädikatenlogik, nämlich der monadischen Prädikatenlogik, als auch als Mengenbeziehungen darstellen. Eine aus heutiger Sicht wesentliche Einschränkung ist, dass die Syllogismen nur Quantoren behandeln können, die mit dem Subjekt der Aussage verbunden sind (wie in Alle Menschen sind sterblich), Quantoren an Objektstelle (wie in Sokrates kennt alle Athener) sind in diesem System nicht behandelbar. Dies wurde erst durch Freges Verwendung von mathematischen Funktionen in der Logik möglich.

Bei der Darstellung als Mengenbeziehungen wird jeder Begriff als sein Umfang (fachsprachlich Extension) interpretiert, d. h. als die Menge der Gegenstände, die unter diesen Begriff fallen. Der Begriff „Mensch“ zum Beispiel wird mengentheoretisch als die Menge aller Menschen interpretiert.

Bei der prädikatenlogischen Interpretation wird jeder Begriff als ein einstelliges Prädikat im Sinn der Prädikatenlogik dargestellt, d. h. als eine einstellige Funktion im mathematischen Sinn, die auf konkrete Individuen angewendet werden kann und die für jedes Individuum die Information liefert, ob es unter diesen Begriff fällt oder nicht. So würde zum Beispiel der Begriff „Mensch“ als das Prädikat „_ ist ein Mensch“ interpretiert. Wendet man dieses Prädikat auf einen Menschen an, zum Beispiel auf Sokrates, dann liefert es den Wahrheitswert „wahr“; wendet man es auf einen Gegenstand an, der kein Mensch ist – zum Beispiel auf ein Tier, auf einen Planeten oder auf eine Zahl –, dann liefert es den Wahrheitswert „falsch“.

Typ

Urteil

Mengenlehre

Prädikatenlogik

A

Alle S sind P.

S\subseteq P

, wobei

S\not =\emptyset

Der (nicht leere) Umfang von S ist eine Teilmenge des Umfangs von P.

\forall x(Sx\rightarrow Px)

, wobei

\exists xSx

Für jedes Individuum gilt: Wenn es ein S ist, dann ist es auch ein P (wobei S nicht leer ist).

E

Keine S sind P.

S\cap P=\emptyset

, wobei

S\not =\emptyset

Die Schnittmenge des (nicht leeren) Umfangs von S und des Umfangs von P ist leer.

\forall x(Sx\rightarrow \neg Px)

, wobei

\exists xSx

Für jedes Individuum gilt: Wenn es ein S ist, dann ist es nicht der Fall, dass es auch ein P ist (wobei S nicht leer ist).

I

Einige S sind P.

S\cap P\neq \emptyset

Die Schnittmenge des Umfangs von S und des Umfangs von P ist nicht leer.

\exists x(Sx\wedge Px)

Es gibt mindestens ein Individuum, das ein S ist und das auch ein P ist.

O

Einige S sind nicht P.

S\not \subseteq P

Der (nicht leere) Umfang von S ist keine Teilmenge des Umfangs von P. (Dass S nicht leer sein kann, ist allerdings schon implizit gegeben, da die leere Menge Teilmenge jeder Menge ist.)

\exists x(Sx\wedge \neg Px)

Es gibt mindestens ein Individuum, das ein S ist und bei dem es nicht der Fall ist, dass es auch ein P ist.

An dieser Formalisierung wurde historisch und auch in jüngerer Zeit Kritik geübt. Dabei wurde die traditionelle Logik als Begriffslogik etwa von Fritz Mauthner der modernen Logik gegenübergestellt, die abschätzig auch als Logistik bezeichnet wurde. Zentral war dabei unter anderem die Frage, ob durch die Formalisierung Existenzpräsuppositionen verloren gehen, die in der vormodernen Lokaltradition als selbstverständlich galten. Auch ist eine direkte Übertragung des logischen Quadrats nicht unproblematisch, wie Michael Wolff in seinem Essay über Frege dargelegt hat.

Walther Brüning reihte die Syllogistik als strenge Syllogistik als einen Sonderfall seiner strengen Logik ein und begegnet dabei den Problemen der klassisch prädikatenlogischen Formalisierung. Er deutet die Urteile als Abkürzungen von sogenannten Geltungswertformeln (siehe: Kategorisches Urteil – Behandlung in der Strengen Logik) und benutzt einen Ableitungsbegriff, der es gestattet alle Syllogismen einfach abzuleiten. Ein vergleichbarer Ansatz ist die differentielle Syllogistik von Albert Menne.

Regeln für die Gültigkeit von Syllogismen

Gültige Syllogismen haben bestimmte Eigenschaften hinsichtlich der Qualität, Quantität und Distribution der in ihnen vorkommenden Begriffe; zum Beispiel kann ein Syllogismus niemals gültig sein, wenn seine Prämissen partikuläre Aussagen sind, seine Konklusion aber eine allgemeine Aussage ist.

Da in Abhängigkeit von der speziellen Interpretation unterschiedlich viele syllogistische Modi gültig sind, gibt es in der Tradition auch unterschiedliche Regelwerke. Im Folgenden werden die heute gängigsten Regeln dargestellt.[20] Sie gehen in dieser einfachen Form auf das Spätmittelalter zurück und sind nicht Teil der antiken, aristotelischen Syllogistik.[21] Das genannte Regelsystem ist der Einfachheit halber redundant, d. h., einige der Regeln lassen sich durch andere ausdrücken.

Regeln der Qualität

Mindestens eine der beiden Prämissen muss eine bejahende Aussage sein (lateinisch ex mere negativis nihil sequitur, „allein aus verneinten Aussagen folgt nichts“).
Zum Beispiel kann aus den Prämissen „Kein Fisch ist Angler“ und „Einige Angler sind keine Fische“ syllogistisch keine Schlussfolgerung gezogen werden.
Wenn beide Prämissen bejahend sind, dann muss auch die Konklusion bejahend sein (lateinisch ambae affirmantes nequeunt generare negantem, „zwei bejahende Aussagen können keine verneinte Aussage erzeugen“).
Wenn eine der beiden Prämissen verneinend ist, dann muss auch die Konklusion verneinend sein.

Regeln der Quantität

Mindestens eine der beiden Prämissen muss eine allgemeine Aussage sein (lateinisch nihil sequitur geminis ex particularibus unquam, „nichts folgt jemals aus partikularen Aussagen“).
Aus den Prämissen „Einige Säugetiere leben im Wasser“ und „Einige Tiere, die auf dem Land leben, sind Säugetiere“ kann ebenfalls syllogistisch nicht geschlossen werden.
Wenn eine der beiden Prämissen eine partikuläre Aussage ist, kann die Konklusion keine allgemeine Aussage sein.

Regeln der Distribution

Der Mittelbegriff muss mindestens einmal distribuiert vorkommen.
Wenn ein Begriff in der Konklusion distribuiert auftritt, muss er auch in einer Prämisse distribuiert auftreten.

Figuren

Welche der drei Begriffe S, P und M in welcher Aussage des Syllogismus vorkommen müssen, ist festgelegt: Der Obersatz besteht aus P und M, der Untersatz aus S und M, die Konklusion aus S und P. Die Konklusion hat dabei immer die Form S – P, die Anordnung der Begriffe in den Prämissen kann frei gewählt werden. Die Reihenfolge, in der die Prämissen aufgeschrieben werden, ist für die Gültigkeit eines Syllogismus zwar unerheblich, dennoch wird bereits seit Aristoteles zuerst der Obersatz und im Anschluss der Untersatz genannt.

Je nach Anordnung der Begriffe in den Prämissen unterscheidet man die vier möglichen Figuren (σχἠματα, schemata):

	1. Figur	2. Figur	3. Figur	4. Figur
erste Prämisse	M – P	P – M	M – P	P – M
zweite Prämisse	S – M	S – M	M – S	M – S
Konklusion	S – P	S – P	S – P	S – P

Beispiel:

Prämisse 1 (oder Obersatz): Alle Menschen (M) sind sterblich (P).

Prämisse 2 (oder Untersatz): Alle Griechen (S) sind Menschen (M).

Konklusion (oder Schlusssatz): Also sind alle Griechen (S) sterblich (P).

Aufgrund der Stellung der Begriffe M – P, S – M, S – P erkennt man einen Syllogismus der 1. Figur.

Modi (Kombinationen) und ihre Merkwörter

Da jede der drei Aussagen in einem Syllogismus von einem der vier Typen A, E, O, I sein kann, gibt es pro Figur $4\times 4\times 4=64$ Möglichkeiten, Aussagen zu einem Syllogismus der jeweiligen Figur zu kombinieren. Jede dieser Möglichkeiten wird ein Modus (Plural: Modi) bzw. eine Kombination der jeweiligen Figur genannt. Bei insgesamt vier verschiedenen Figuren gibt es so insgesamt $64\times 4=256$ Kombinationsmöglichkeiten, d. h. 256 Typen von Syllogismen. Unter diesen 256 Modi sind 24 gültige und 232 nicht gültige Syllogismen.

Ein Modus wird durch drei Buchstaben beschrieben. Dabei stehen die ersten beiden Buchstaben für die Typen der Prämissen, der dritte Buchstabe für den Typ der Konklusion.

Beispiel:

Prämisse 1 (oder Obersatz): Alle Krimis (M) sind spannend (P).

Prämisse 2 (oder Untersatz): Einige Bücher (S) sind Krimis (M).

Konklusion (oder Schlusssatz): Also sind einige Bücher (S) spannend (P).

Prämisse 1 ist vom Typ A, Prämisse 2 vom Typ I, die Konklusion folglich ebenfalls vom Typ I. Es handelt sich also um einen Syllogismus vom Typ A–I–I.

Die 24 gültigen Modi werden traditionell mit folgenden Merkwörtern bezeichnet:

1. Figur: Barbara, Celarent, Darii, Ferio, Barbari, Celaront

2. Figur: Baroco, Cesare, Camestres, Festino, Camestrop, Cesaro

3. Figur: Bocardo, Darapti, Datisi, Disamis, Felapton, Ferison

4. Figur: Bamalip, Calemes, Dimatis, Fesapo, Fresison, Calemop

In diesen Merkwörtern bezeichnen die Vokale die Typen der Aussagen in der Reihenfolge Obersatz–Untersatz–Konklusion; zum Beispiel bezeichnet Modus Darii einen Syllogismus der ersten Figur und vom Typ A–I–I. Die Konsonanten geben an, auf welchen Syllogismus der 1. Figur (erster Konsonant) der jeweilige Syllogismus zurückgeführt werden kann und durch welche Veränderung (jeweils auf Vokal folgender Konsonant) diese Zurückführung möglich ist (siehe Abschnitt Reduktion auf die erste Figur).

Zu beachten ist, dass in der Tradition unterschiedliche Versionen der Merkwörter kursieren. Die ältesten überlieferten Versionen dieser mnemotechnischen Syllogistik stammen von den scholastischen Logikern William of Sherwood[22] und Petrus Hispanus[23] um 1240/1250, wobei die Priorität unsicher ist.

Die fünf nicht fett gedruckten Modi sind jeweils „schwache“ Folgerungen eines fett gedruckten „starken“ Modus der jeweiligen Figur. „Stark“ bedeutet dabei, dass die Konklusion eine allgemeine Aussage (A oder E) ist; „schwach“ bedeutet, dass die Konklusion eine partikuläre Aussage (I oder O) ist, die eine direkte Folgerung der jeweiligen starken Aussage ist. Es wird davon ausgegangen, dass schwache Modi erstmals 50 v. Chr. von Ariston von Alexandria thematisiert wurden.[3]

Beispiele:

Modus Barbara (stark): Alle Münchner sind Bayern, alle Schwabinger sind Münchner, es folgt: Alle Schwabinger sind Bayern.
Modus Barbari (schwach): Alle Münchner sind Bayern, alle Schwabinger sind Münchner, es folgt: Einige Schwabinger sind Bayern.
Modus Celarent (stark): Kein Münchner ist Passauer, alle Schwabinger sind Münchner, es folgt: Kein Schwabinger ist Passauer.
Modus Celaront (schwach): Kein Münchner ist Passauer, alle Schwabinger sind Münchner, es folgt: Einige Schwabinger sind keine Passauer.

Die schwachen Schlussfolgerungen sind logisch gültig, sofern gewisse Zusatzbedingungen erfüllt sind: Jeweils bestimmte Begriffe (Subjekt, Prädikat oder Mittelbegriff) dürfen nicht leer sein (siehe auch Abschnitt Existenzielle Voraussetzungen).

Reduktion auf die erste Figur

Mit einigen einfachen Umformungen, die in den Konsonanten der traditionellen Merkwörter kodiert sind, lassen sich die Modi aller Figuren auf einen Modus der ersten Figur zurückführen („reduzieren“). Diese Tatsache war bereits Aristoteles bekannt, der auch entsprechende Umformungsregeln formuliert hat und der die erste Figur als die vollkommene, Syllogismen der ersten Figur als vollkommenen Syllogismus (τέλειος συλλογισμός – téleios syllogismós) bezeichnete.

Der Anfangsbuchstabe des jeweiligen traditionellen Merkwortes gibt an, auf welchen Modus der ersten Figur der jeweilige Modus zurückgeführt werden kann: Modi, deren Name mit „B“ beginnt, lassen sich auf den Modus Barbara zurückführen; Modi, deren Name mit „C“ beginnt, lassen sich auf den Modus Celarent zurückführen; und ebenso lassen sich Modi, deren Name mit „D“ bzw. mit „F“ beginnt, auf den Modus Darii bzw. Ferio zurückführen.

Die Umformungen der Syllogistik sind Schlussregeln im formalen Sinn, d. h., das Resultat jeder syllogistischen Umformung einer Aussage bzw. eines Syllogismus folgt aus der umgeformten Aussage bzw. aus dem umgeformten Syllogismus.

Die für die Reduktion erforderlichen Umformungen sind im Folgenden näher beschrieben; zusätzlich wird im Abschnitt Beispiele und Reduktion auf die erste Figur für jeden syllogistischen Modus ein Beispiel genannt und dessen Reduktion auf die erste Figur gezeigt.

Einfache Umwandlung

Bei der einfachen Umwandlung (lat. conversio simplex) werden Subjekt und Prädikat der jeweiligen Aussage vertauscht; so wird aus der Aussage „Einige Philosophen sind Griechen“ nach der einfachen Umwandlung die Aussage „Einige Griechen sind Philosophen“. In den Merkwörtern wird die einfache Umwandlung einer Aussage durch den Buchstaben „s“ hinter dem der betroffenen Aussage zugeordneten Vokal angezeigt; zum Beispiel muss beim Reduzieren des Modus Cesare die erste Prämisse, eine E-Aussage, einer einfachen Umwandlung unterzogen werden.

Einfache Umwandlung ist nur bei Aussagen der Typen E und I möglich: Wenn keine Schweine Schafe sind, dann sind auch keine Schafe Schweine (E-Aussage); und wenn einige Griechen Philosophen sind, dann sind auch einige Philosophen Griechen (I-Aussage). Für die A- und O-Aussage ist keine einfache Umwandlung möglich: Wenn alle Philosophen Menschen sind, heißt das nämlich noch lange nicht, dass alle Menschen Philosophen sind (A-Aussage); und wenn einige Menschen keine Politiker sind, heißt das noch lange nicht, dass einige Politiker keine Menschen sind (O-Aussage). Tatsächlich sind unter den traditionellen Merkwörtern nur solche, bei denen das „s“ auf ein „e“ oder „i“ folgt.

Normalerweise wird die einfache Umwandlung auf die jeweilige Prämisse des zu reduzierenden Syllogismus angewendet. Steht das „s“ jedoch am Ende des Merkwortes, dann wird nicht die Konklusion des zu reduzierenden Syllogismus der einfachen Umwandlung unterzogen, sondern die Konklusion jenes Syllogismus der ersten Figur, auf den reduziert werden soll. Ein Beispiel für diesen Sonderfall ist der Modus Dimatis: Er wird auf einen Modus Datisi zurückgeführt, in dessen Konklusion Subjekt und Prädikat vertauscht werden, also auf einen Syllogismus der Form „Alle P sind M. Einige M sind S. Also sind einige P S.“

Umwandlung durch Einschränkung

Bei der Umwandlung durch Einschränkung (lat. conversio per accidens) wird zusätzlich zur Vertauschung von Subjekt und Prädikat der jeweiligen Aussage ihr Typ von A auf I bzw. von E auf O geändert. So wird zum Beispiel aus der A-Aussage „Alle Schweine sind rosa“ nach der Umwandlung durch Einschränkung die I-Aussage „Einige rosa (Dinge) sind Schweine“ und wird aus der E-Aussage „Keine Schweine sind Schafe“ die O-Aussage „Einige Schafe sind keine Schweine“. In den Merkwörtern wird die Umwandlung durch Einschränkung durch den Buchstaben „p“ hinter dem der betroffenen Aussage zugeordneten Vokal angezeigt.

Auch bei dieser Umwandlung liegt ein Sonderfall vor, wenn das „p“ im Merkwort nach dem dritten Vokal – also am Wortende – steht: In diesem Fall bezieht es sich wie bei der einfachen Umwandlung nicht auf die Konklusion des zu reduzierenden Syllogismus, sondern auf die Konklusion des resultierenden Syllogismus der ersten Figur.

Vertauschung der Prämissen

Vertauschung der Prämissen (lat. mutatio praemissarum) ist für die Reduktion all jener Modi erforderlich, in deren Merkwörtern der Konsonant „m“ an beliebiger Stelle vorkommt. Unabhängig von der Position des Konsonanten „m“ im jeweiligen Merkwort darf die Vertauschung der Prämissen erst nach jeder allenfalls erforderlichen einfachen Umwandlung und nach jeder allenfalls erforderlichen Umwandlung durch Einschränkung ausgeführt werden.

Indirekter Beweis

Modi, in deren Merkwörtern der Konsonant „c“ vorkommt, aber nicht am Wortanfang steht, – also nur die Modi Baroco und Bocardo – lassen sich nur durch einen indirekten Beweis (lat. reductio ad absurdum)[24] auf die erste Figur zurückführen. Zu diesem Behuf wird die Wahrheit der A-Prämisse des zu reduzierenden Syllogismus (im Fall von Baroco also die erste, im Fall von Bocardo die zweite Prämisse) sowie das kontradiktorische Gegenteil, d. h. die Negation der Konklusion angenommen. Auf diese Weise entsteht ein Modus Barbara, dessen Konklusion der O-Prämisse des zu reduzierenden Syllogismus widerspricht. Da die Annahme, die Konklusion treffe nicht zu, solcherart zu einem Widerspruch geführt hat, ist gezeigt, dass die Konklusion zutreffen muss.

Im Detail ausgeführt wird der indirekte Beweis in den Abschnitten AOO – Modus Baroco und OAO – Modus Bocardo.

Abweichende Darstellungen

Hinsichtlich der genauen Formulierung der Umwandlungsregeln gibt es bei den einzelnen Autoren Unterschiede; insbesondere ist es üblich,[25] auf den hier dargebrachten Sonderfall bei der einfachen Umwandlung und bei der Umwandlung durch Einschränkung zu verzichten und die Konsonanten „s“ und „p“ auch am Wortende auf den umzuwandelnden Syllogismus zu beziehen und nicht – wie hier dargestellt – auf den Ziel-Syllogismus. Diese Formulierung würde aber die Reduktion der beiden Modi „Bamalip“ und „Camestrop“ in der dargestellten Form unmöglich machen, weil weder für eine I-Aussage noch für eine O-Aussage eine Umwandlung durch Einschränkung möglich ist.

Zur ersten Figur des kategorischen Syllogismus

Die erste Figur hat folgende Form:

	Obersatz: M – P
	Untersatz: S – M
Es folgt:	Konklusion: S – P

Ihre gültigen Modi sind Barbara, Celarent, Darii, Ferio, Barbari und Celaront.

AAA – Modus Barbara

Beispiel

	Alle Rechtecke sind Vierecke
	Alle Quadrate sind Rechtecke
Es folgt:	Alle Quadrate sind Vierecke

EAE – Modus Celarent

Beispiel

	Kein Rechteck ist ein Kreis
	Alle Quadrate sind Rechtecke
Es folgt:	Kein Quadrat ist ein Kreis

AII – Modus Darii

Beispiel

	Alle Quadrate sind Rechtecke
	Einige Rhomben sind Quadrate
Es folgt:	Einige Rhomben sind Rechtecke

EIO – Modus Ferio

Beispiel

	Kein Säugetier atmet mit Kiemen
	Einige Wassertiere sind Säugetiere
Es folgt:	Einige Wassertiere atmen nicht mit Kiemen

AAI – Modus Barbari

Beispiel

	Alle Rechtecke sind Vierecke
	Alle Quadrate sind Rechtecke
Es folgt:	Einige Quadrate sind Vierecke

Anmerkung: Barbari ist insofern ein abgeleiteter Modus, als seine Konklusion eine schwächere Folgerung der Konklusion von Modus Barbara ist: Wenn alle Quadrate Rechtecke sind, dann sind insbesondere auch einige Quadrate Rechtecke. Traditionell wird ein durch Abschwächung der Konklusion aus einem anderen Modus abgeleiteter Modus auch als schwacher Modus bezeichnet.

EAO – Modus Celaront

Beispiel

	Kein Rechteck ist ein Kreis
	Alle Quadrate sind Rechtecke
Es folgt:	Einige Quadrate sind keine Kreise

Anmerkung: Die Konklusion von Celaront ist eine Abschwächung der Konklusion von Celarent: Wenn keine Quadrate Kreise sind, dann sind insbesondere auch einige Quadrate keine Kreise. Celaront wird daher traditionell als schwacher Modus bezeichnet.

Zur zweiten Figur des kategorischen Syllogismus und ihrer Reduktion auf die erste Figur

Die zweite Figur hat folgende Form:

	Obersatz: P – M
	Untersatz: S – M
Es folgt:	Konklusion: S – P

Die gültigen Modi der zweiten Figur sind Baroco, Cesare, Camestres, Festino, Camestrop und Cesaro.

AOO – Modus Baroco

Beispiel

	Alle Professoren sind ernst
	Einige Dozenten sind nicht ernst
Es folgt:	Einige Dozenten sind nicht Professoren

Reduktion des Beispiels auf die erste Figur: Der Modus Baroco ist einer von nur zwei Modi, in deren Merkwort der Konsonant „c“ vorkommt, aber nicht am Wortanfang steht. Diese Konstellation zeigt an, dass zur Rückführung auf die erste Figur ein indirekter Beweis erforderlich ist. Für diesen indirekten Beweis wird ein Syllogismus konstruiert, dessen erste Prämisse die A-Prämisse des zu reduzierenden Syllogismus ist – im Beispiel also die Aussage „Alle Professoren sind ernst.“ Als zweite Prämisse des zu konstruierenden Syllogismus wird die kontradiktorische Verneinung der Konklusion des zu reduzierenden Syllogismus verwendet – im Beispiel also die Aussage „Alle Dozenten sind Professoren“ (dieses A-Urteil ist die Verneinung des O-Urteils „Einige Dozenten sind nicht Professoren“, vergleiche Logisches Quadrat). Da das Merkwort „Baroco“ mit einem „B“ beginnt, werden die so aufgestellten Prämissen zu einem Syllogismus des Modus Barbara ergänzt, der dann vollständig lautet: „Alle Professoren sind ernst. Alle Dozenten sind Professoren. Also sind alle Dozenten ernst.“ Die Schlussfolgerung, dass alle Dozenten ernst sind, ist aber mit der O-Prämisse des zu reduzierenden Syllogismus unverträglich, die gerade lautete „Einige Dozenten sind nicht ernst“. Somit ist gezeigt, dass die Annahme, die Konklusion des zu reduzierenden Syllogismus treffe nicht zu, zu einem Widerspruch führt. Die Konklusion des zu reduzierenden Syllogismus muss daher zutreffen, der zu reduzierende Syllogismus also gültig sein.

EAE – Modus Cesare

Beispiel

	Kein Säugetier atmet durch Kiemen
	Alle Fische atmen durch Kiemen
Es folgt:	Kein Fisch ist ein Säugetier

Reduktion des Beispiels auf die erste Figur: Das Merkwort „Cesare“ beginnt mit einem „C“, der Syllogismus muss sich daher auf einen Modus Celarent zurückführen lassen. Im Merkwort „Cesare“ steht unmittelbar nach dem „e“, das den Typ der ersten Prämisse angibt, der Buchstabe „s“, der die einfache Umwandlung der betroffenen Aussage einfordert. Wandelt man die erste Prämisse einfach um, entsteht die Aussage „Kein Kiemenatmer ist ein Säugetier“. Weitere bedeutungstragende Konsonanten kommen im Merkwort „Cesare“ nicht vor, deshalb ist die Umwandlung damit abgeschlossen. Tatsächlich ist der so entstandene Syllogismus „Kein Kiemenatmer (M) ist ein Säugetier (P). Alle Fische (S) atmen durch Kiemen (M). Also ist kein Fisch (S) ein Säugetier (P).“ ein Syllogismus vom Typ Celarent.

AEE – Modus Camestres

Beispiel

	Alle Fische atmen durch Kiemen
	Kein Säugetier atmet durch Kiemen
Es folgt:	Kein Säugetier ist ein Fisch

Reduktion des Beispiels auf die erste Figur: Der Anfangsbuchstabe „C“ des Merkwortes „Camestres“ zeigt an, dass die Reduktion zu einem Modus Celarent führen muss. Das „s“ nach dem Vokal „e“ der zweiten Prämisse zeigt an, dass jene einer einfachen Umwandlung unterzogen werden muss; dabei entsteht die neue Aussage „Kein Kiemenatmer ist ein Säugetier“. Das „m“ zeigt – ungeachtet seiner konkreten Position – an, dass die Prämissen nach allen anderen allfälligen Umformungen ausgetauscht werden müssen: Es entsteht der Syllogismus „Kein Kiemenatmer ist ein Säugetier. Alle Fische atmen durch Kiemen. Also ist kein Säugetier ein Fisch.“ Am Wortende des Merkwortes Camestres steht ein weiteres „s“, das an dieser Stelle eine einfache Umwandlung der Konklusion des Zielmodus, also des Celarent erfordert – und tatsächlich ist der Syllogismus „Kein Kiemenatmer ist ein Säugetier. Alle Fische atmen durch Kiemen. Also ist kein Säugetier ein Fisch.“ ein Modus Celarent, in dessen Konklusion die Stellung von Subjekt und Prädikat vertauscht ist.

EIO – Modus Festino

Beispiel

	Kein Tier, das mit Kiemen atmet, ist ein Säugetier
	Einige Wassertiere sind Säugetiere
Es folgt:	Einige Wassertiere atmen nicht mit Kiemen

Reduktion des Beispiels auf die erste Figur: Der Anfangsbuchstabe „F“ zeigt an, dass der Syllogismus sich auf einen Modus Ferio zurückführen wird lassen. Der Buchstabe „s“ nach dem ersten Vokal im Merkwort „Festino“ weist darauf hin, dass die erste Prämisse einer einfachen Umwandlung unterzogen werden muss; dabei entsteht die neue Aussage „Kein Säugetier atmet mit Kiemen“. Das Merkwort enthält keine weiteren bedeutungstragenden Konsonanten, und tatsächlich ist der durch diese eine Umwandlung entstandene Syllogismus „Kein Säugetier atmet mit Kiemen. Einige Wassertiere sind Säugetiere. Es folgt: Einige Wassertiere atmen nicht mit Kiemen.“ vom erwarteten Typ Ferio; die Reduktion ist damit erfolgreich abgeschlossen.

Zur dritten Figur des kategorischen Syllogismus und ihrer Reduktion auf die erste Figur

Die dritte Figur hat folgende Form:

	Obersatz: M – P
	Untersatz: M – S
Es folgt:	Konklusion; S – P

Die gültigen Modi der dritten Figur sind Bocardo, Datisi, Disamis, Ferison, Darapti und Felapton.

OAO – Modus Bocardo

Beispiel

	Einige Münchner sind nicht Politiker
	Alle Münchner sind Stadtbewohner
Es folgt:	Einige Stadtbewohner sind nicht Politiker

Reduktion des Beispiels auf die erste Figur: Das Merkwort „Bocardo“ enthält im Wortinneren den Konsonanten „c“, der die Notwendigkeit eines indirekten Beweises anzeigt. Für diesen wird ein neuer Syllogismus gebildet, dessen Prämissen die A-Prämisse des Bocardo – im Beispiel also die Aussage „Alle Münchner sind Stadtbewohner“ – und die Verneinung der Konklusion des Bocardo ist: Verneint man die O-Aussage „Einige Stadtbewohner sind nicht Politiker“, dann entsteht die A-Aussage „Alle Stadtbewohner sind Politiker“. Da das Merkwort „Bocardo“ mit einem „B“ beginnt, ordnet man diese beiden Prämissen so an und ergänzt sie so um eine Konklusion, dass ein Syllogismus der Form Barbara entsteht. Für das Beispiel lautet dieser Syllogismus „Alle Stadtbewohner sind Politiker. Alle Münchner sind Stadtbewohner. Also sind alle Münchner Politiker.“ Die Konklusion, „Alle Münchner sind Politiker“, widerspricht nun gerade der ersten Prämisse des zu reduzierenden Syllogismus, der Aussage „Einige Münchner sind nicht Politiker“; es ist daher gezeigt, dass die Annahme, die Konklusion des Bocardo – also die Aussage „Einige Stadtbewohner sind nicht Politiker“ – sei falsch, zu einem Widerspruch führt – sie muss daher richtig sein.

AII – Modus Datisi

Beispiel

	Alle Rechtecke sind Vierecke
	Einige Rechtecke sind Quadrate
Es folgt:	Einige Vierecke sind Quadrate

Reduktion des Beispiels auf die erste Figur: Das Merkwort „Datisi“ enthält als einzigen bedeutungstragenden Konsonanten den Buchstaben „s“ unmittelbar nach dem Vokalzeichen für die zweite Prämisse; diese muss daher einer einfachen Umwandlung unterzogen werden, d. h., ihr Subjekt und ihr Prädikat müssen ausgetauscht werden. Aus dieser Operation entsteht der Syllogismus „Alle Rechtecke sind Vierecke. Einige Quadrate sind Rechtecke. Also sind einige Vierecke Quadrate.“ Dieser Syllogismus ist von der Form Darii, die Reduktion damit abgeschlossen.

IAI – Modus Disamis

Beispiel

	Einige Früchte sind Äpfel
	Alle Früchte sind Teile von Pflanzen
Es folgt:	Einige Teile von Pflanzen sind Äpfel

Reduktion des Beispiels auf die erste Figur: Das Merkwort „Disamis“ zeigt an, dass für die Reduktion auf einen Modus Darii zwei einfache Umwandlungen (Buchstabe „s“ hinter dem die jeweilige Aussage bezeichnenden Vokal), d. h. eine Vertauschung von Subjekt und Prädikat, sowie eine Vertauschung der Prämissen (Buchstabe „m“ an beliebiger Stelle) erforderlich sein wird. Einfache Umwandlungen der Prämissen müssen immer vor einer allfälligen Vertauschung ausgeführt werden. „Disamis“ fordert die einfache Umwandlung der ersten Prämisse, dabei entsteht der Satz „Einige Äpfel sind Früchte“. Für die zweite Prämisse fordert das Merkwort „Disamis“ keine Aktion, sodass im nächsten Schritt schon die Vertauschung der Prämissen (Buchstabe „m“) ausgeführt werden kann. Der dabei entstehende Syllogismus lautet „Alle Früchte sind Teile von Pflanzen. Einige Äpfel sind Früchte. Also sind einige Teile von Pflanzen Äpfel.“ An letzter Stelle – unmittelbar nach dem Vokal, der die Konklusion bezeichnet – enthält das Merkwort „Disamis“ ein weiteres „s“. Die Umwandlung der Konklusion – egal ob einfach oder durch Einschränkung – ist ein Sonderfall, weil hier nicht die Konklusion des zu reduzierenden Syllogismus gemeint ist, sondern die Konklusion des Modus, auf den reduziert werden soll. Das „s“ ist also an dieser Stelle die Anweisung, in der Konklusion von Modus Darii Subjekt und Prädikat auszutauschen, was zu einem Syllogismus der Gestalt „Alle M sind P. Einige S sind M. Also sind einige P S.“ führt. Dieses ist die Gestalt des reduzierten Disamis-Syllogismus: „Alle Früchte (M) sind Teile von Pflanzen (P). Einige Äpfel (S) sind Früchte (M). Also sind einige Teile von Pflanzen (P) Äpfel (S).“ Damit ist die Reduktion abgeschlossen.

EIO – Modus Ferison

Beispiel

	Keine Münchner sind Passauer
	Einige Münchner sind Studenten
Es folgt:	Einige Studenten sind nicht Passauer

Reduktion des Beispiels auf die erste Figur: Das Merkwort „Ferison“ enthält nur einen bedeutungstragenden Konsonanten, das „s“ unmittelbar nach dem Vokal für die zweite Prämisse. Dies zeigt an, dass die zweite Prämisse einer einfachen Umwandlung unterzogen werden muss, d. h. einer Vertauschung ihres Subjekts und ihres Prädikats. Der so entstandene Syllogismus, „Keine Münchner sind Passauer. Einige Studenten sind Münchner. Also sind einige Studenten nicht Passauer.“, ist bereits ein Syllogismus der ersten Figur, und zwar – das Merkwort „Ferison“ beginnt mit einem „F“ – vom Typ Ferio.

AAI – Modus Darapti

Beispiel

	Alle Quadrate sind Rechtecke
	Alle Quadrate sind Vierecke
Es folgt:	Einige Vierecke sind Rechtecke

Anmerkung: Der Modus Darapti setzt voraus, dass das Subjekt nicht leer ist, dass es im Beispiel also tatsächlich Quadrate gibt; vergleiche Abschnitt Existenzielle Voraussetzungen.
Reduktion des Beispiels auf die erste Figur: Der Anfangsbuchstabe des Merkwortes „Darapti“ zeigt an, dass sich der Syllogismus auf den Modus Darii reduzieren lassen wird. An bedeutungstragenden Konsonanten enthält das Merkwort „Darapti“ nur das „p“, das eine Umwandlung durch Einschränkung bezeichnet. Das „p“ steht unmittelbar nach dem Vokal der zweiten Prämisse, also ist sie es, die durch Einschränkung umgewandelt werden muss. Bei der Umwandlung durch Einschränkung werden Subjekt und Prädikat des Satzes ausgetauscht und wird die Quantität der Aussage von allgemein auf partikulär geändert, entsteht also aus der Aussage „Alle Quadrate sind Vierecke“ die Aussage „Einige Vierecke sind Quadrate“. Da es keine weiteren bedeutungstragenden Konsonanten im Merkwort „Darapti“ gibt, ist die Reduktion an dieser Stelle abgeschlossen und ist der so entstandene Syllogismus „Alle Quadrate sind Rechtecke. Einige Vierecke sind Quadrate. Also sind einige Vierecke Rechtecke.“ ein Modus Darii.

EAO – Modus Felapton

Beispiel

	Keine Münchner sind Passauer
	Alle Münchner sind Stadtbewohner
Es folgt:	Einige Stadtbewohner sind keine Passauer

Anmerkung: Der Modus Felapton setzt voraus, dass der Mittelbegriff nicht leer ist, dass es im Beispiel also tatsächlich Münchner gibt; vergleiche Abschnitt Existenzielle Voraussetzungen.

Reduktion des Beispiels auf die erste Figur: Modus Felapton wird sich mit einer Umwandlung durch Einschränkung (Buchstabe „p“) auf einen Modus Ferio reduzieren lassen. Das „p“ steht im Merkwort „Felapton“ hinter dem Vokal, der die zweite Prämisse bezeichnet; daher ist sie es, die umgewandelt werden muss. Bei der Umwandlung durch Einschränkung werden Subjekt und Prädikat der betroffenen allgemeinen Aussage ausgetauscht und wird sie zu einer partikulären Aussage umgewandelt: Aus „Alle Münchner sind Stadtbewohner“ wird „Einige Stadtbewohner sind Münchner.“ Der so entstandene Syllogismus „Keine Münchner sind Passauer. Einige Stadtbewohner sind Münchner. Also sind einige Stadtbewohner keine Passauer.“ ist von der Gestalt des Modus Ferio – die Reduktion ist damit abgeschlossen.

Zur vierten Figur des kategorischen Syllogismus und ihrer Reduktion auf die erste Figur

Die vierte Figur hat folgende Form:

	Obersatz: P – M
	Untersatz: M – S
Es folgt:	Konklusion: S – P

Die gültigen Modi der vierten Figur sind Calemes, Dimatis, Fresison, Bamalip, Calemop und Fesapo.

AAI – Modus Bamalip

Beispiel

	Alle Quadrate sind Rechtecke
	Alle Rechtecke sind Vierecke
Es folgt:	Einige Vierecke sind Quadrate

Anmerkung: Der Modus Bamalip setzt voraus, dass das Subjekt nicht leer ist, dass es im Beispiel also tatsächlich Quadrate und Rechtecke gibt (wobei die Existenz letzterer in diesem Fall aus der Existenz ersterer bereits folgt); vergleiche Abschnitt Existenzielle Voraussetzungen.

Reduktion des Beispiels auf die erste Figur: Für die Prämissen hat das Merkwort „Bamalip“ lediglich die eine Handlungsanweisung parat, ihre Reihenfolge zu vertauschen (Konsonant „m“ an beliebiger Stelle). Der zweite bedeutungstragende Konsonant im Wortinneren ist das „p“, das zu einer Umwandlung durch Einschränkung – d. h. eine Vertauschung von Subjekt und Prädikat einer Aussage sowie ihre Veränderung ihrer Quantität von allgemein (A, E) zu partikulär (I, O) – auffordert. Nun steht das „p“ aber am Wortende – dies ist der Sonderfall, bei dem nicht die Konklusion des zu reduzierenden Syllogismus umgewandelt werden muss, sondern die Konklusion des Syllogismus, auf den reduziert werden soll. Reduziert werden soll – das Merkwort „Bamalip“ beginnt mit „B“ – auf Barbara, und unterzieht man dessen Konklusion, „Alle S sind P“, einer Umwandlung durch Einschränkung, so lautet sie „Einige P sind S“. Dem solcherart aus Modus Barbara entstandenen Syllogismus „Alle M sind P. Alle S sind M. Also sind einige P S.“ entspricht nun aber genau der umgeformte Syllogismus Bamalip, „Alle Rechtecke (M) sind Vierecke (P). Alle Quadrate (S) sind Rechtecke (M). Also sind einige Vierecke (P) Quadrate (S).“ Bamalip ist damit auf die erste Figur zurückgeführt.

AEE – Modus Calemes

Beispiel

	Alle Passauer sind Bayern
	Keine Bayern sind Sachsen
Es folgt:	Keine Sachsen sind Passauer

Reduktion des Beispiels auf die erste Figur: Reduziert wird auf einen Modus Celarent, wie der Anfangsbuchstabe des Merkworts „Calemes“ anzeigt. Der letzte Vokal in „Calemes“ wird vom bedeutungstragenden Konsonanten „s“ gefolgt, der eine einfache Umwandlung der Konklusion in demjenigen Syllogismus anfordert, auf den reduziert werden soll. Wandelt man den Modus Celarent entsprechend um, d. h., vertauscht man in seiner Konklusion Subjekt und Prädikat, entsteht der Modus „Keine M sind P. Alle S sind M. Also sind keine P S.“ Auf diesen lässt sich Modus Calemes reduzieren, und zwar – der einzige weitere bedeutungstragende Konsonant im Merkwort „Calemes“ ist das „m“ – durch eine Vertauschung seiner Prämissen. Der so entstehende Syllogismus ist von der gewünschten Gestalt: „Keine Bayern (M) sind Sachsen (P). Alle Passauer (S) sind Bayern (M). Also sind keine Sachsen (P) Passauer (S).“

IAI – Modus Dimatis

Beispiel

	Einige Rauten sind Rechtecke
	Alle Rechtecke sind Parallelogramme
Es folgt:	Einige Parallelogramme sind Rauten

Reduktion des Beispiels auf die erste Figur: Reduziert wird auf Darii, wie der Anfangsbuchstabe des Merkwortes „Dimatis“ anzeigt. Das „m“ fordert eine Vertauschung der Prämissen. Das „s“ am Wortende zeigt die Notwendigkeit einer einfachen Umwandlung – d. h. Vertauschung von Subjekt und Prädikat – der Konklusion des Ziel-Syllogismus, also des Darii an. Tatsächlich hat der entstandene Syllogismus die Gestalt eines Modus Darii mit derart umgewandelter Prämisse: „Alle Rechtecke (M) sind Parallelogramme (P). Einige Rauten (S) sind Rechtecke (M). Also sind Einige Parallelogramme (P) Rauten (S).“

EAO – Modus Fesapo

Beispiel

	Keine Passauer sind Münchner
	Alle Münchner sind Stadtbewohner
Es folgt:	Einige Stadtbewohner sind keine Passauer

Anmerkung: Der Modus Fesapo setzt voraus, dass der Mittelbegriff nicht leer ist, dass es im Beispiel also tatsächlich Münchner gibt; vergleiche Abschnitt Existenzielle Voraussetzungen.

Reduktion des Beispiels auf die erste Figur: Um den Syllogismus auf einen Modus Ferio zurückzuführen (das Merkwort „Fesapo“ beginnt mit einem „F“) muss die erste Prämisse einer einfachen Umwandlung unterzogen werden (unmittelbar nach dem ersten Vokal im Merkwort „Fesapo“ steht ein „s“) und muss die zweite Prämisse einer Umwandlung durch Einschränkung unterzogen werden (unmittelbar nach dem zweiten Vokal im Merkwort „Fesapo“ steht ein „p“). Der solcherart entstehende Syllogismus ist tatsächlich vom Typ Ferio: „Keine Münchner (M) sind Passauer (P). Einige Stadtbewohner (S) sind Münchner (M). Also sind einige Stadtbewohner (S) keine Passauer (P).“

EIO – Modus Fresison

Beispiel

	Keine Passauer sind Münchner
	Einige Münchner sind Studenten
Es folgt:	Einige Studenten sind keine Passauer

Reduktion des Beispiels auf die erste Figur: Um einen Modus Fresison auf die erste Figur zu reduzieren, müssen beide Prämissen einer einfachen Umwandlung unterzogen werden, denn das Merkwort Fresison enthält sowohl unmittelbar nach dem ersten Vokal als auch unmittelbar nach dem zweiten Vokal den Konsonanten „s“. Weitere bedeutungstragende Konsonanten sind nicht enthalten, sodass der durch diese beiden Umwandlungen entstehende Syllogismus bereits die Form eines Modus Ferio (das Merkwort „Fresison“ beginnt mit einem „F“) der ersten Figur hat: „Keine Münchner (M) sind Passauer (P). Einige Studenten (S) sind Münchner (M). Also sind einige Studenten (S) keine Passauer (P).“

Wesentlich verschiedene Syllogismen

Die Equivalenzen "XeY genau dann falls YeX" und ebenso "XiY genau wenn YiX" erlauben es, Syllogismen in mehreren Paaren miteinander zu identifizieren, im EIO-Fall sogar vier, durch alle vier Figuren. Dann bleibt eine verkürzte Liste von nur acht Syllogismen übrig, falls noch Abschwächungen gestrichen werden: Barbara, Darii, Felapton, Ferio, Camestres, Celarent, Bocardo und Baroco.

Siehe auch

Begriffslogik
Syllogismen in der traditionellen Rhetorik:
- Enthymem – teilweise als Syllogismus verstandener Schluss, oft in verkürzter Darstellung
- Epicherem – Syllogismus, in dem jede Prämisse ihrerseits ein verkürzter Syllogismus ist
Subsumtion – Syllogismus in juristischen Arbeiten

Literatur

Aristoteles: Erste Analytiken I. Aristoteles: Analytica Priora. Buch I. Übersetzt und erläutert von Theodor Ebert und Ulrich Nortmann. Berlin: Akademie Verlag, 2007 ISBN 978-3-05-004427-9 (mit umfangreichem Kommentar)
Aristoteles: Analytica Posteriora. Übersetzung und Kommentar von Wolfgang Detel. Berlin, Akademie-Verlag 1998. ISBN 3-05-001796-1. (mit umfangreichem Kommentar)
Aristoteles: Organon. Griechisch-Deutsch. Übersetzung und Kommentar von H.G. Zekl. 4 Teile in 3 Bänden, Meiner 2001, ISBN 3-7873-1596-9. (die Übersetzung ist bei ihrem ersten Erscheinen äußerst scharf als unbrauchbar kritisiert worden; vgl. die Rezension von Hermann Weidemann in: Zeitschrift für philosophische Forschung 53, 1999, Seite 602–610)
Aristoteles: Topik. Ditzingen: Reclam 2004. (=Reclams Universal-Bibliothek 18337) ISBN 3-15-018337-5, ISBN 978-3-15-018337-3.
Helmut Gätje: Bemerkungen zum System der Syllogismen. Universität des Saarlandes, Fach Orientalistik, Saarbrücken 1978.
Bruno von Freytag-Löringhoff: Über das System der modi des Syllogismus. In: Zeitschrift für philosophische Forschung. Bd. 4, Nr. 2/1949, S. 235–256.
Günther Patzig: Die aristotelische Syllogistik. Logisch-philologische Untersuchung über das Buch A der „Ersten Analytik“. 3. Aufl., Göttingen, 1969.
Albert Menne: Logik und Existenz. (Eine logistische Analyse der kategorischen Syllogismusfunktoren und das Problem der Nullklasse) Meisenheim 1954.
Michael Wolff: Abhandlung über die Prinzipien der Logik. Mit einer Rekonstruktion der aristotelischen Syllogistik. Zweite, verbesserte und erweiterte Auflage, Frankfurt am Main: Klostermann 2009. ISBN 978-3-465-03639-5.
in englischer Sprache:
- Otto Bird: Syllogistic and Its Extensions, Englewood Cliffs: Prentice-Hall 1964. (einfache Darstellung)
- William Kneale, Martha Kneale: The Development of Logic, Clarendon Press 1962. ISBN 0-19-824773-7. (Standardwerk zur Geschichte der Logik)
- Jan Łukasiewicz: Aristotle's Syllogistic from the Standpoint of Modern Formal Logic, Oxford: Clarendon Press ²1957, danach Taylor & Francis 1987, ISBN 0-8240-6924-2. und Oxford University Press 1998 (=Oxford University Press Academic Monograph Reprints), ISBN 0-19-824144-5. (Standardwerk der modernen Syllogismusforschung)
- Paul Thom: The Syllogism, München: Philosophia 1981, ISBN 3-88405-002-8.

Weblinks

Commons: Syllogismen – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Syllogismus – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Robin Smith: Aristotle's Logic. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Henrik Lagerlund: Medieval Theories of the Syllogism. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Terence Parsons: The Traditional Square of Opposition. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Niko Strobach: Neuere Interpretationen der aristotelischen Syllogistik (PDF; 112 kB)
Edward D. Buckner. (Hg.): Square of Opposition (Textsammlung, engl.)
syllogistisches Online-Programm
Computational Aristotelian Term Logic (Memento vom 17. Juli 2009 im Internet Archive) – ausführliches Syllogistisches Online-Programm in englischer Sprache

Einzelnachweise

Übersetzung Wagner/Rapp
So unterscheidet noch Meyers Großes Konversations-Lexikon von 1905 bis 1909 zwischen dem Syllogismus im weiteren Sinn („in der Logik im allgemeinen der Schluß überhaupt“ – Band 19, Seite 234) vom Syllogismus im engeren Sinn (dem „kategorischen S[chluss], dem Syllogismus des Aristoteles“ – Band 17, Seite 877).
„Logic“, in: The New Encyclopaedia Britannica, Chicago u. a. 15. Aufl. 2003, Band 23, Seite 263
Albert Veraart: Galenische Figur, in: Jürgen Mittelstraß: Enzyklopädie Philosophie und Wissenschaftstheorie. Metzler Stuttgart 1996, ISBN 3-476-02012-6, 1. Band, Seite 699
„Logic“, in: The New Encyclopaedia Britannica, Chicago u. a. 15. Aufl. 2003, Band 23, Seite 265
N. I. Kondakow: Wörterbuch der Logik. VEB Bibliographisches Institut Leipzig 1. Aufl. 1978, Seite 410
Jan Łukasiewicz: Aristotle's Syllogistic from the Standpoint of Modern Formal Logic, Oxford: Clarendon Press ²1957.
„The result [of Łukasiewicz's] is something of great interest, but very different from Aristotle's own conception of his work“ (Kneale/Kneale: The Development of Logic, Seite 80)
Günther Patzig: Die aristotelische Syllogistik. Logisch-philologische Untersuchung über das Buch A der „Ersten Analytik“. 3. Aufl., Göttingen, 1969.
Niko Strobach: Neuere Interpretationen der aristotelischen Syllogistik (PDF; 112 kB), Seite 13, insbesondere das dort gebrachte Prior-Zitat „The Prior Analytics ... is not a book of syllogisms, but a book about syllogisms, and the statement ‚If B is predicable of every M, and M of every A, then B is predicable of every A‘ is a perfectly natural way of talking about syllogisms of the form ‚Every B is M, and every M is A, therefore etc.‘, and saying that all such syllogisms are valid.“
Gereon Wolters: Syllogistik, in: Jürgen Mittelstraß: Enzyklopädie Philosophie und Wissenschaftstheorie. Metzler Stuttgart 1996, ISBN 3-476-02012-6, 4. Band, Seite 156–158, Seite 157, Spalte 2
Als Beispiel für diese Sicht sei die Duden-Grammatik von 1966 genannt (Duden Band 4, 2. Auflage 1966, § 6020 c, Seite 540), die das Wort „sterblich“ in diesem Zusammenhang als eine Form von Umstandsergänzung betrachtet, genauer als Artergänzung (§ 5280, Seite 481): „Um eine Artergänzung handelt es sich aber auch dort, wo die Artangabe den ‚kopulativen‘ Verben folgt, weil wir ihr auch in diesen Fällen den Wert eines selbständigen Satzgliedes zusprechen[.]“ (§ 5285, Seite 481) bzw. „Neuere Auffassungen sprechen auch [den Kopulaverben] den gleichen Rang [eines Prädikats] zu“ (§ 5125, Seite 473)
Ein Beispiel für diese Sicht ist die aktuelle Duden-Grammatik: „Prädikativverben verbinden sich mit einem Subjekts- oder Objektsprädikativ zu einem mehrteiligen Prädikat. Hierzu gehören die so genannten Kopulaverben [wie] sein“ (Duden Band 4, 7. Auflage 2005, § 577, Seite 421)
„Since the seventeenth century most writers have adopted the suggestion of John Philoponus that the major term be defined as the predicate of the conclusion“ (Kneale/Kneale: The Development of Logic, Seite 71)
„[I]t would probably be a mistake to lay much emphasis on the distinction. For in the detailed application of his theory Aristotle reasons as though his conditional statements were in effect rules of inference rather than theses.“ (Kneale/Kneale: The Development of Logic, Seite 80)
Christian Thiel: Logisches Quadrat, in: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. 1. Aufl. 1995, 2004, Band 3, Seite 423
siehe z. B. Niko Strobach: Neuere Interpretationen der aristotelischen Syllogistik (PDF; 112 kB), Seite 5f.
„In order to justify Aristotle's doctrine as a whole it is necessary, then, that he assumed application for all the general terms with which he dealt.“ (Kneale/Kneale: The Development of Logic, Seite 60, Hervorhebung im Original)
Diese Variante der Definition entlehnt sich aus „Distribution“, in: Encyclopaedia Britannica, Band 4, 15. Aufl. 2003, Seite 129
siehe Bird 1964, Seite 20–22
„A simple set of rules of validity was finally produced in the later Middle Ages, based on the concept of Distribution.“ (C. L. Hamblin: Fallacies. Methuen London 1970, ISBN 0-416-70070-5, Seite 195)
siehe C. L. Hamblin: Fallacies. Methuen London 1970. ISBN 0-416-70070-5, Seite 117, wo allerdings in Fußnote 1 darauf hingewiesen wird, dass es Vorläufer gebe.
Kneale/Kneale: The Development of Logic, Seite 231–234
Die Darstellung des indirekten Beweises im Syllogismus folgt sehr eng „Logic“, in: The New Encyclopaedia Britannica, Chicago u. a. 15. Aufl. 2003, Band 23, Seite 262f.
z. B. auch im Standardlehrbuch Otto Bird: Syllogistic and Its Extensions, Englewood Cliffs: Prentice-Hall 1964, Seite 27ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Übersetzung Wagner/Rapp

[2] So unterscheidet noch Meyers Großes Konversations-Lexikon von 1905 bis 1909 zwischen dem Syllogismus im weiteren Sinn („in der Logik im allgemeinen der Schluß überhaupt“ – Band 19, Seite 234) vom Syllogismus im engeren Sinn (dem „kategorischen S[chluss], dem Syllogismus des Aristoteles“ – Band 17, Seite 877).

[neb23-263-3] „Logic“, in: The New Encyclopaedia Britannica, Chicago u. a. 15. Aufl. 2003, Band 23, Seite 263

[4] Albert Veraart: Galenische Figur, in: Jürgen Mittelstraß: Enzyklopädie Philosophie und Wissenschaftstheorie. Metzler Stuttgart 1996, ISBN 3-476-02012-6, 1. Band, Seite 699

[5] „Logic“, in: The New Encyclopaedia Britannica, Chicago u. a. 15. Aufl. 2003, Band 23, Seite 265

[6] N. I. Kondakow: Wörterbuch der Logik. VEB Bibliographisches Institut Leipzig 1. Aufl. 1978, Seite 410

[7] Jan Łukasiewicz: Aristotle's Syllogistic from the Standpoint of Modern Formal Logic, Oxford: Clarendon Press ²1957.

[8] „The result [of Łukasiewicz's] is something of great interest, but very different from Aristotle's own conception of his work“ (Kneale/Kneale: The Development of Logic, Seite 80)

[9] Günther Patzig: Die aristotelische Syllogistik. Logisch-philologische Untersuchung über das Buch A der „Ersten Analytik“. 3. Aufl., Göttingen, 1969.

[10] Niko Strobach: Neuere Interpretationen der aristotelischen Syllogistik (PDF; 112 kB), Seite 13, insbesondere das dort gebrachte Prior-Zitat „The Prior Analytics ... is not a book of syllogisms, but a book about syllogisms, and the statement ‚If B is predicable of every M, and M of every A, then B is predicable of every A‘ is a perfectly natural way of talking about syllogisms of the form ‚Every B is M, and every M is A, therefore etc.‘, and saying that all such syllogisms are valid.“

[11] Gereon Wolters: Syllogistik, in: Jürgen Mittelstraß: Enzyklopädie Philosophie und Wissenschaftstheorie. Metzler Stuttgart 1996, ISBN 3-476-02012-6, 4. Band, Seite 156–158, Seite 157, Spalte 2

[12] Als Beispiel für diese Sicht sei die Duden-Grammatik von 1966 genannt (Duden Band 4, 2. Auflage 1966, § 6020 c, Seite 540), die das Wort „sterblich“ in diesem Zusammenhang als eine Form von Umstandsergänzung betrachtet, genauer als Artergänzung (§ 5280, Seite 481): „Um eine Artergänzung handelt es sich aber auch dort, wo die Artangabe den ‚kopulativen‘ Verben folgt, weil wir ihr auch in diesen Fällen den Wert eines selbständigen Satzgliedes zusprechen[.]“ (§ 5285, Seite 481) bzw. „Neuere Auffassungen sprechen auch [den Kopulaverben] den gleichen Rang [eines Prädikats] zu“ (§ 5125, Seite 473)

[13] Ein Beispiel für diese Sicht ist die aktuelle Duden-Grammatik: „Prädikativverben verbinden sich mit einem Subjekts- oder Objektsprädikativ zu einem mehrteiligen Prädikat. Hierzu gehören die so genannten Kopulaverben [wie] sein“ (Duden Band 4, 7. Auflage 2005, § 577, Seite 421)

[14] „Since the seventeenth century most writers have adopted the suggestion of John Philoponus that the major term be defined as the predicate of the conclusion“ (Kneale/Kneale: The Development of Logic, Seite 71)

[15] „[I]t would probably be a mistake to lay much emphasis on the distinction. For in the detailed application of his theory Aristotle reasons as though his conditional statements were in effect rules of inference rather than theses.“ (Kneale/Kneale: The Development of Logic, Seite 80)

[16] Christian Thiel: Logisches Quadrat, in: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. 1. Aufl. 1995, 2004, Band 3, Seite 423

[17] siehe z. B. Niko Strobach: Neuere Interpretationen der aristotelischen Syllogistik (PDF; 112 kB), Seite 5f.

[18] „In order to justify Aristotle's doctrine as a whole it is necessary, then, that he assumed application for all the general terms with which he dealt.“ (Kneale/Kneale: The Development of Logic, Seite 60, Hervorhebung im Original)

[19] Diese Variante der Definition entlehnt sich aus „Distribution“, in: Encyclopaedia Britannica, Band 4, 15. Aufl. 2003, Seite 129

[20] siehe Bird 1964, Seite 20–22

[21] „A simple set of rules of validity was finally produced in the later Middle Ages, based on the concept of Distribution.“ (C. L. Hamblin: Fallacies. Methuen London 1970, ISBN 0-416-70070-5, Seite 195)

[22] siehe C. L. Hamblin: Fallacies. Methuen London 1970. ISBN 0-416-70070-5, Seite 117, wo allerdings in Fußnote 1 darauf hingewiesen wird, dass es Vorläufer gebe.

[23] Kneale/Kneale: The Development of Logic, Seite 231–234

[24] Die Darstellung des indirekten Beweises im Syllogismus folgt sehr eng „Logic“, in: The New Encyclopaedia Britannica, Chicago u. a. 15. Aufl. 2003, Band 23, Seite 262f.

[25] z. B. auch im Standardlehrbuch Otto Bird: Syllogistic and Its Extensions, Englewood Cliffs: Prentice-Hall 1964, Seite 27ff.