Homosphäre und Heterosphäre
Neben der üblichen Einteilung einer Atmosphäre und speziell der Erdatmosphäre nach ihrem vertikalen Temperaturgradienten ist in der Meteorologie auch die Unterscheidung zwischen Homosphäre (von griech. ὁμός homós „gleich“) und Heterosphäre (von griech. ἕτερος héteros „der andere“, „ungleich“) gebräuchlich. In der Homosphäre sind die Atmosphärengase gut durchmischt, in der darüber liegenden Heterosphäre beginnen sich die Atmosphärenbestandteile mit wachsender Höhe zunehmend zu entmischen.
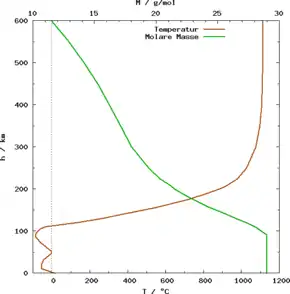
In einer Höhe von ca. 100 km ändert sich die Charakteristik der beiden Kurven. Hier liegt die Grenze zwischen Homosphäre (unterhalb) und Heterosphäre (oberhalb).
Der Übergangsbereich zwischen beiden wird als Homopause oder Turbopause bezeichnet, dieser liegt im Fall der Erde in einer Höhe von etwa 80 bis 120 Kilometern.
Skalenhöhe und Entmischung
Gemäß der Boltzmann-Statistik nimmt die Dichte eines Gases, welches sich in einem homogenen Gravitationsfeld im thermischen Gleichgewicht befindet, exponentiell mit der Höhe ab. Die Höhendifferenz H, über welche hinweg die Dichte jeweils um einen Faktor e = 2,718… fällt, ist die Skalenhöhe der betreffenden Atmosphäre, und es gilt:
mit
| R | : | universelle Gaskonstante |
| T | : | absolute Temperatur |
| M | : | molare Masse |
| g | : | Erdbeschleunigung |
Da die Gase, aus welchen sich die Erdatmosphäre zusammensetzt, unterschiedliche molare Massen aufweisen, sind auch die Skalenhöhen dieser Luftbestandteile zum Teil sehr verschieden. Für eine Temperatur von 0 °C beispielsweise betragen die Skalenhöhen von[1]
| Argon | : | H = 5.980 m |
| molekularem Sauerstoff | : | H = 7.480 m |
| molekularem Wasserstoff | : | H = 119.500 m. |
Auch wenn die idealisierten Voraussetzungen für diese beispielhaften Rechnungen in der realen Erdatmosphäre nicht strikt erfüllt sind (insbesondere die Lufttemperatur in unterschiedlichen Höhen sehr variabel ist), so wäre dennoch grundsätzlich zu erwarten, dass die Atmosphäre sich teilweise entmischt, dass also die schweren Bestandteile mit geringer Skalenhöhe sich in Bodennähe konzentrieren und in größeren Höhen die leichteren Bestandteile mit größerer Skalenhöhe vorherrschen.
Homosphäre
Die Beobachtung zeigt jedoch, dass in der Troposphäre und im Wesentlichen auch in der Stratosphäre und Mesosphäre die Zusammensetzung der Atmosphäre praktisch unabhängig von der Höhe ist. Turbulenzen und großräumige Vertikalbewegungen durchmischen die Atmosphäre in diesem Bereich konvektiv so wirksam, dass sich keine Entmischung durchsetzen kann. Diese gut durchmischte Schicht, die sich bis in eine Höhe von etwa 100 km erstreckt, wird als Homosphäre bezeichnet.[2]
Aufgrund der konstanten Zusammensetzung weist das Gemisch „Luft“ bis in eine Höhe von etwa 80 km[3] stets dieselbe mittlere Molmasse von etwa 29 g/mol auf. Barometrische Höhenformeln können daher die Luft bis in jene Höhen als einheitliches Gas mit dieser Molmasse behandeln.
Allerdings nimmt der Wasserdampfgehalt in der Troposphäre mit der Höhe stark ab, weil die mit der Höhe absinkende Temperatur immer geringere maximale Dampfdrücke zulässt. So ist der Wasserdampfdruck in 10 km Höhe typischerweise auf etwa 1 ‰ des Bodenwertes gefallen (der Luftdruck hingegen nur auf 25 % des Bodendrucks).[4]
Auch die höhenabhängige Bildung von Ozon und anderen Spurengasen führt zu einer ebenfalls höhenabhängigen Konzentration dieser Luftkomponenten.[3]
Die Homosphäre der Erde enthält mit über 99,9 % der Teilchen den hauptsächlichen Anteil der Atmosphäre. Die Höhe von 100 km (Kármán-Linie) wird seitens der Fédération Aéronautique Internationale als Grenze zum Weltraum angesehen, da hier (bei einer Temperatur von −80 °C und einem Luftdruck von 0,03 Pascal, also 0,00003 % des Luftdrucks auf Meereshöhe)[5] die zum Erhalt des Auftriebs benötigte Fluggeschwindigkeit den Wert der Bahngeschwindigkeit erreicht, welche zum Erhalt einer Erdumlaufbahn benötigt wird. Diese Definition der Grenze zwischen Luft- und Weltraum ist international weitestgehend anerkannt, wenngleich zum Beispiel die NASA diese Grenze abweichend schon bei der Mesopause ansetzt.
Heterosphäre
In größeren Höhen treten wegen der zunehmenden freien Weglängen (in Bodennähe: etwa 0,06 μm, in 100 km Höhe: etwa 15 cm, in 200 km Höhe: etwa 200 m[1]) von der Molmasse abhängige molekulare Diffusionsvorgänge auf. Somit findet in diesem als Heterosphäre bezeichneten Bereich die von der Boltzmann-Statistik verlangte gaskinetische Entmischung tatsächlich statt:[1] z. B. ist die mittlere Molmasse der Luft in 700 km Höhe auf etwa 16 g/mol zurückgegangen (entspricht atomarem Sauerstoff) und sinkt in noch größeren Höhen auf 4 g/mol (Helium) und schließlich 1 g/mol (Wasserstoff).[6]
Die großen freien Weglängen bewirken, dass sich die Gasteilchen kaum mehr zu kollektiven Bewegungsvorgängen zusammenfinden können, so dass es in der Heterosphäre praktisch keine Winde mehr gibt. Abgasfahnen aufsteigender Raketen werden daher in der Homosphäre meist durch Höhenwinde wechselnder Richtung verschleppt, ohne dass sich ihr Durchmesser wesentlich ändert, während sie in der Heterosphäre schnell auseinanderdiffundieren.[6]
Neben der gaskinetischen Entmischung beeinflusst auch die durch die Ultraviolettstrahlung der Sonne ausgelöste Dissoziationsvorgänge die Zusammensetzung der Atmosphäre. Oberhalb von etwa 80 km Höhe dissoziieren Kohlendioxid und die verbliebenen Reste von Wasserdampf. Die Dissoziation von O2-Molekülen in O-Atome, welche bereits in einer Höhe von etwa 30 km beginnt und dort zur Bildung von Ozon führt, erzeugt ab etwa 100 km Höhe nur noch freie O-Atome. Oberhalb von etwa 150 km existieren nur noch Spuren von O2.[7]
Einzelnachweise
- W. Roedel: Physik unserer Umwelt: Die Atmosphäre. 3. Auflage. Springer, Berlin 2000, ISBN 3-540-67180-3. S. 63
- G. H. Liljequist, K. Cehak: Allgemeine Meteorologie. 3. Auflage. Vieweg, Braunschweig/Wiesbaden 1994, ISBN 3-528-23555-1, S. 380
- F. Möller: Einführung in die Meteorologie. Band 1, BI-Wissenschaftsverlag, Mannheim/Wien/Zürich 1991, ISBN 3-411-00276-X, S. 52
- F. Möller: Einführung in die Meteorologie. Band 1, BI-Wissenschaftsverlag, Mannheim/Wien/Zürich 1991, ISBN 3-411-00276-X, S. 140
- NOAA, NASA, USAF: U.S. Standard Atmosphere, 1976, Washington, D.C. 1976, S. 68: für Z = 100000 m: t = -78.07 °C, P = 3,2011e-4 mb, P/P0 = 3,1593e-7
- F. Möller: Einführung in die Meteorologie. Band 1, BI-Wissenschaftsverlag, Mannheim/Wien/Zürich 1991, ISBN 3-411-00276-X, S. 55
- F. Möller: Einführung in die Meteorologie. Band 1, BI-Wissenschaftsverlag, Mannheim/Wien/Zürich 1991, ISBN 3-411-00276-X, S. 54
